7: Аналіз двоваріантних кількісних даних
- Page ID
- 97376
Протягом останніх трьох розділів ви дізналися про те, як зробити висновки для одноваріантних даних. Для кожного дослідницького питання, яке можна було задати, для відповіді знадобилася лише одна випадкова величина. Ця випадкова величина може бути або категоричною, або кількісною. У деяких випадках одну і ту ж випадкову величину можна вибірку та порівнювати для двох різних популяцій, але це все одно робить її одноманітними даними. У цьому розділі ми розглянемо двоваріантні кількісні дані. Це означає, що для кожної одиниці в нашій вибірці будуть визначені дві кількісні змінні. Мета збору двох кількісних змінних полягає в тому, щоб визначити, чи існує взаємозв'язок між ними.
Останній раз аналіз двох кількісних змінних обговорювався в главі 4, коли ви навчилися робити розкид графік і знаходити кореляцію. У той час було підкреслено, що навіть якщо існує кореляція, цього факту недостатньо для підтвердження причинно-наслідкового зв'язку. Існує безліч можливих пояснень, які можуть бути надані для спостережуваної кореляції. Вони були перераховані в розділі 4 і знову надані тут.
- Зміна змінної x призведе до зміни змінної y
- Зміна змінної y призведе до зміни змінної x
- Може існувати цикл зворотного зв'язку, в якому зміна змінної x призводить до зміни змінної y, що призводить до іншої зміни змінної x тощо.
- Зміни обох змінних визначаються третьою змінною
- Зміни в обох змінних є випадковими.
- Кореляція є результатом викидів, без яких не було б значної кореляції.
- Кореляція є результатом плутанини змінних.
Причинність легше довести маніпулятивним експериментом, ніж спостережливим експериментом. У маніпулятивному експерименті дослідник буде випадковим чином розподіляти суб'єктів до різних груп, тим самим зменшуючи будь-який можливий ефект від плутанини змінних. У спостережливих експериментах змішані змінні не можуть бути розподілені справедливо по всій досліджуваної популяції. Маніпулятивні експерименти не завжди можна проводити через етичні причини. Наприклад, земля в даний час проходить спостережний експеримент, в якому пояснювальною змінною є кількість викопного палива, що перетворюється на вуглекислий газ, а змінна відгуку - середня глобальна температура. Було б визнано неетичним, якби вчений запропонував у 1800-х роках, що ми повинні спалити якомога більше викопного палива, щоб побачити, як це впливає на глобальну температуру. Так само експерименти, які змусять когось палити, писати текст під час водіння або робити інші небезпечні дії, не будуть вважатися етичними, і тому кореляції слід шукати за допомогою спостережних експериментів.
Існує кілька причин, за якими доцільно збирати та аналізувати двоваріантні дані. Однією з таких причин є те, що залежна змінна або змінна відповіді представляє більший інтерес, але незалежну або пояснювальну змінну легше виміряти. Тому, якщо існує сильний зв'язок між пояснювальною та змінною відповіді, цей зв'язок може бути використаний для обчислення змінної відповіді за допомогою даних пояснювальної змінної. Наприклад, лікар дуже хотів би знати, в якій мірі блокуються коронарні артерії пацієнта, але дані про артеріальний тиск легше отримати. Тому, оскільки існує міцна залежність між артеріальним тиском і ступенем блокування артерій, то артеріальний тиск можна використовувати як інструмент прогнозування.
Ще однією причиною збору та аналізу двоваріантних даних є встановлення норм для населення. Як приклад, немовлята зважуються і вимірюються при народженні, і повинна бути кореляція між їх вагою та довжиною (зростом?). Дитина, яка має суттєву недостатню вагу порівняно з немовлятами однакової довжини, викликає занепокоєння у лікаря.
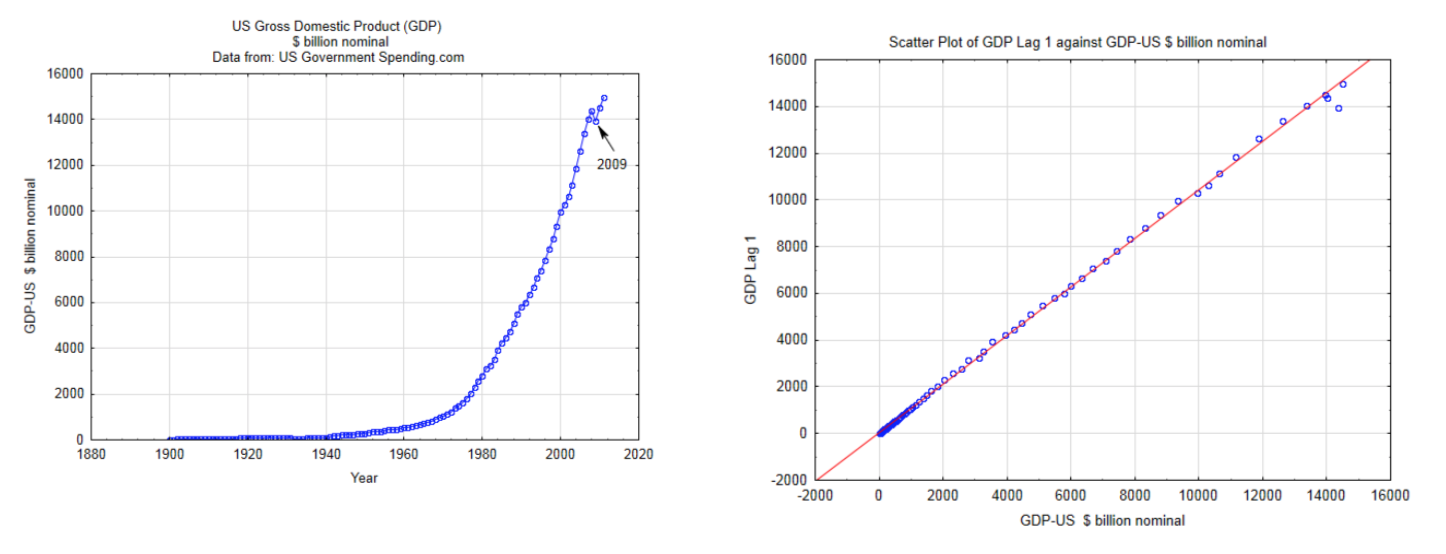
Для того щоб використовувати методи, описані в цьому розділі, дані повинні бути незалежними, кількісними, безперервними і мати двоваріантний нормальний розподіл. Використання дискретних кількісних даних перевищує сферу дії цієї глави. Незалежність означає, що величина одного значення даних не впливає на величину іншого значення даних. Це часто порушується при використанні даних часових рядів. Наприклад, дані річного ВВП (валового внутрішнього продукту) не повинні використовуватися як одна з випадкових величин для двоваріантного аналізу даних, оскільки розмір економіки за один рік має величезний вплив на її розмір наступного року. Це показано на двох графіках нижче. Графік зліва - графік часових рядів фактичного ВВП США. Графік праворуч - це графік розкиду, який використовує ВВП для США як змінну x та ВВП для США через рік (лаг 1) для значення y. Той факт, що ці точки знаходяться в такій прямій, говорить про те, що дані не є незалежними. Отже, ці дані не повинні використовуватися в тому типі аналізів, які будуть розглянуті в цьому розділі.
Двоваріантний нормальний розподіл - це той, в якому значення y зазвичай розподіляються для кожного значення x, а значення x зазвичай розподіляються для кожного значення y. Якби це можна було пофарбувати в трьох вимірах, поверхня виглядала б як гора із закругленою вершиною.
Тепер ми повернемося до прикладу в главі 4, в якому було досліджено взаємозв'язок між розривом у багатстві, виміряним коефіцієнтом Джині, та бідністю. Життя може бути складнішим для тих, хто перебуває в бідності, і, безумовно, вплив, який вони можуть мати в країні, набагато більш обмежений, ніж ті, хто багатий. Оскільки люди в бідності повинні спрямовувати свою енергію на виживання, вони мають менше часу і енергії, щоб покласти на речі, які принесуть користь людству в цілому. Тому в інтересах всіх людей знайти спосіб зменшити бідність і тим самим збільшити кількість людей, здатних допомогти світу покращитися.
Є багато можливих змінних, які можуть сприяти бідності. Частковий список наведено нижче. Не всі з них є кількісними змінними, і деякі з них важко виміряти, але вони все ще можуть впливати на рівень бідності.
- Освіта
- Рівень доходу батьків
- Рівень доходу громади
- Наявність вакансій
- Психічне здоров'я
- Знання
- Мотивація і рішучість
- Інвалідність або хвороба
- Розрив у багатстві
- Раса/Етнічніка/Імміграційний статус/стать
- Відсоток населення, яке зайнято
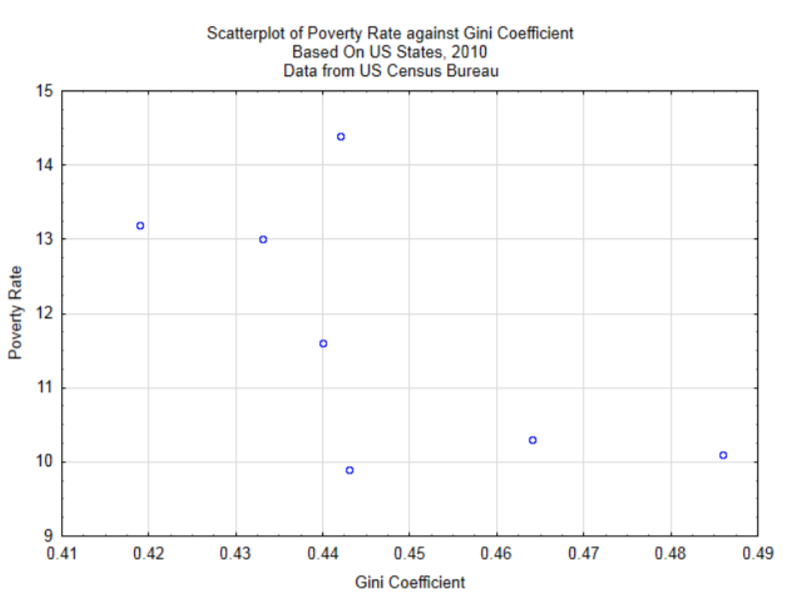
У главі 4 було досліджено лише взаємозв'язок між розривом у багатстві та рівнем бідності. Дані були зібрані з семи станів, щоб визначити, чи існує кореляція між цими двома змінними. Графік розкиду відтворюється нижче. Кореляція становить -0,65.
Нагадуємо, що кореляція - це число між -1 і 1. Кореляція населення представлена грецькою літерою\(\rho\), тоді як коефіцієнт кореляції вибірки представлений буквою\(r\). Кореляція 0 вказує на відсутність кореляції, тоді як кореляція 1 або -1 вказує на ідеальну кореляцію. Питання полягає в тому, чи має основна популяція значну лінійну залежність. Докази цього надходять з зразка. Гіпотези, які зазвичай перевіряються:
\(H_0: \rho = 0\)
\(H_1: \rho \ne 0\)
Це двоххвостий тест для ненаправленої альтернативної гіпотези. Значний результат свідчить лише про те, що кореляція не дорівнює 0, вона не вказує на напрямок кореляції.
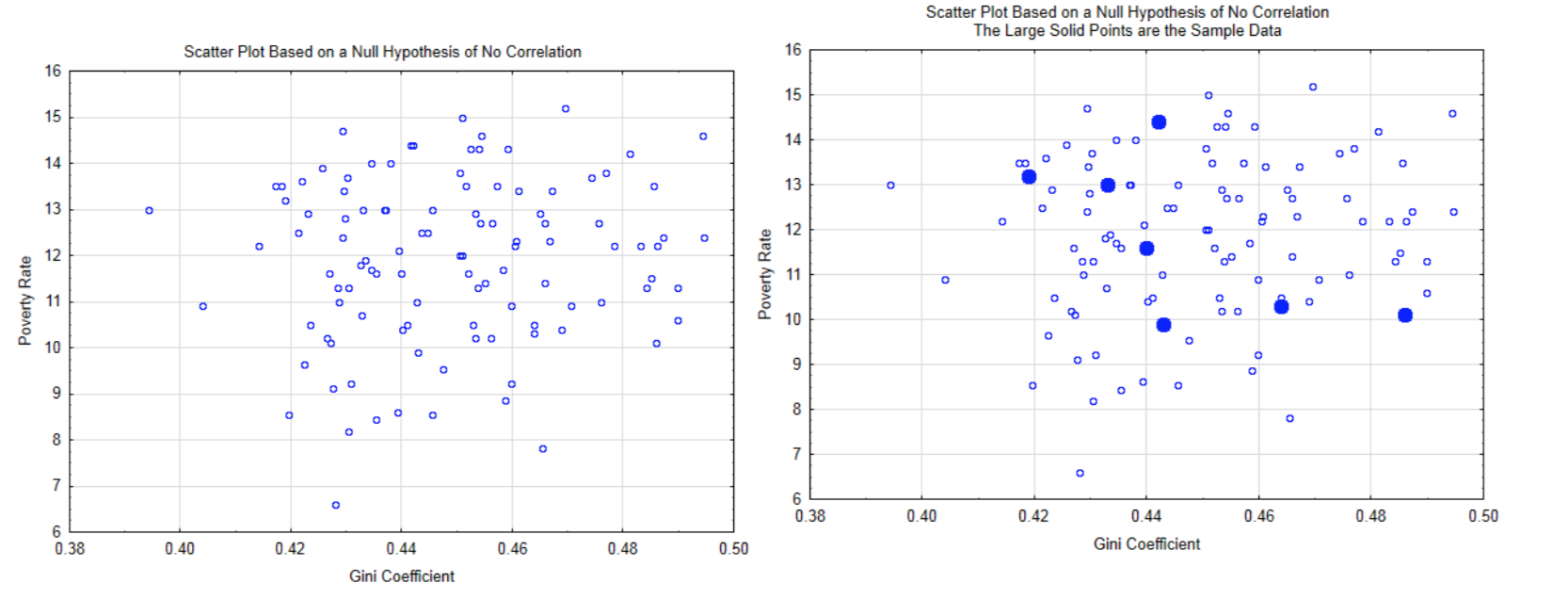
Логіка цього тесту гіпотези базується на припущенні, що нульова гіпотеза вірна, що означає відсутність кореляції в популяції. Приклад показаний на графіку розкиду зліва. З цього розподілу розраховується ймовірність отримання даних вибірки (показаних суцільними колами на графіку праворуч), або більш екстремальних даних (утворюючи більш пряму лінію).
Тест, який використовується для визначення того, чи є кореляція значною, є тестом t. Формула така:
\[t = \dfrac{r\sqrt{n - 2}}{\sqrt{1 - r^2}}.\]
Розрізняють n - 2 ступені свободи.
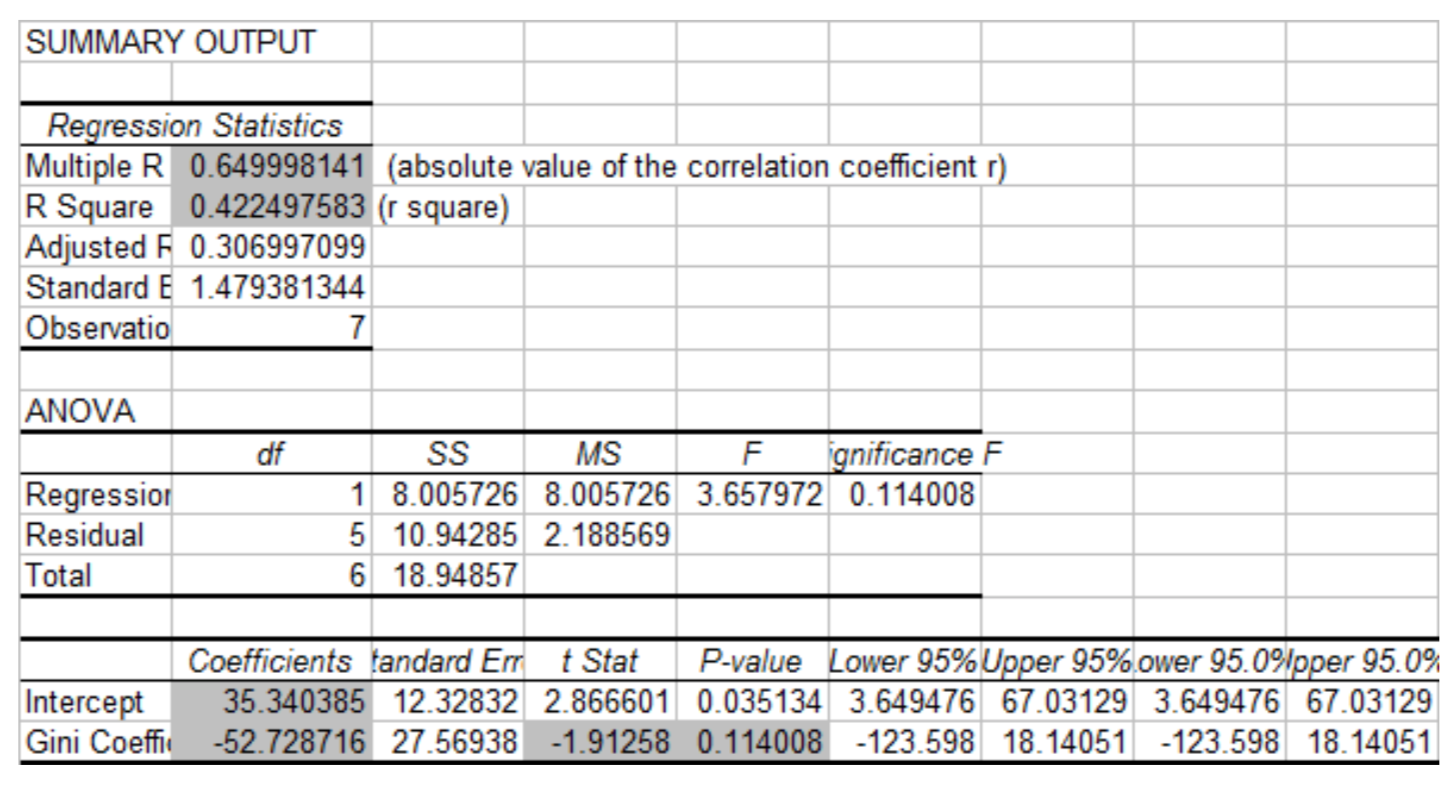
Це можна продемонструвати на прикладі коефіцієнтів Джині та рівня бідності, як це передбачено в главі 4, та використовуючи рівень значущості 0,05. Кореляція становить -0,650. Розмір вибірки дорівнює 7, тому існує 5 ступенів свободи. Після підстановки в тестову статистику\(t = \dfrac{-0.650 \sqrt{7 - 2}}{\sqrt{1 - (-0.650)^2}}\), значення тестової статистики становить -1,91. Виходячи з t-таблиці з 5 ступенями свободи, двостороннє p-значення більше 0,10 (фактичне 0,1140). Отже, не існує значної кореляції між коефіцієнтом Джині та рівнем бідності.
Ще однією пояснювальною змінною, яку можна дослідити на предмет її кореляції з рівнем бідності, є співвідношення зайнятості та населення (відсотки). Це відсоток населення, яке зайнято не менше однієї години в місяці.
. 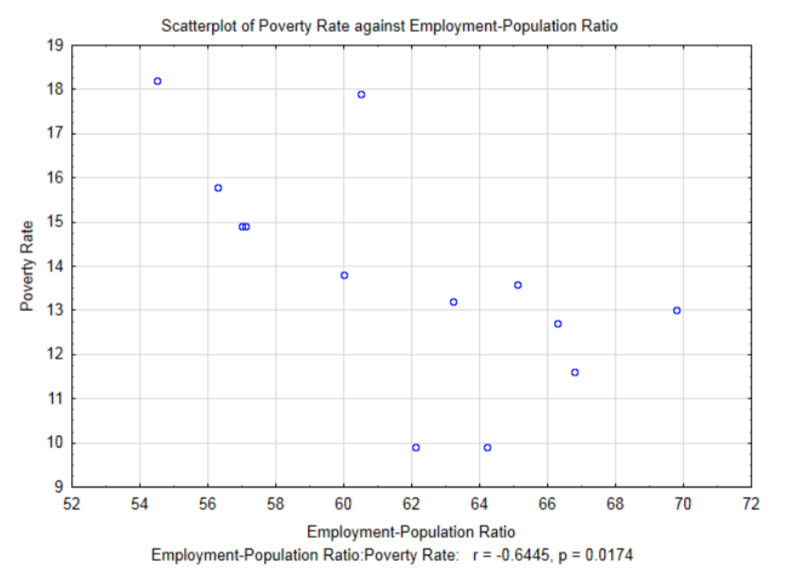
Кореляція для цих даних становить -0,6445,\(t\) = -2,80 і\(p\) = 0,0174. Зверніть увагу на рівні 0.05 значущості, ця кореляція є значною. Перш ніж досліджувати значення значної кореляції, порівняйте результати кореляції між коефіцієнтом Джині та рівнем бідності, який становив -0,650, та результати кореляції між коефіцієнтом зайнятості та населення та рівнем бідності, який становить -0,6445. Колишня кореляція не була значною, тоді як пізніша була значною, хоча вона менша, ніж перша. Це хороший приклад того, чому знання коефіцієнта кореляції не є достатньою інформацією, щоб визначити, чи є кореляція значною. Іншим фактором, що впливає на визначення значущості, є розмір вибірки. Дані про співвідношення зайнятості населення та рівня бідності визначали з більшого розміру вибірки (13 порівняно з 7). Розмір вибірки відіграє важливу роль у визначенні, чи підтримується альтернатива. З дуже великими зразками дуже малі кореляції вибірки можуть бути показані значними. Питання в тому, чи відповідає значне важливе.
Вплив розміру вибірки на можливі кореляції показано у чотирьох розподілах нижче. Ці розподіли були створені, починаючи з популяції, яка мала кореляцію\(\rho = 0.000\) 0,10 000 зразків розміром 5,15,35, і 300 були взяті з цієї популяції з заміною.
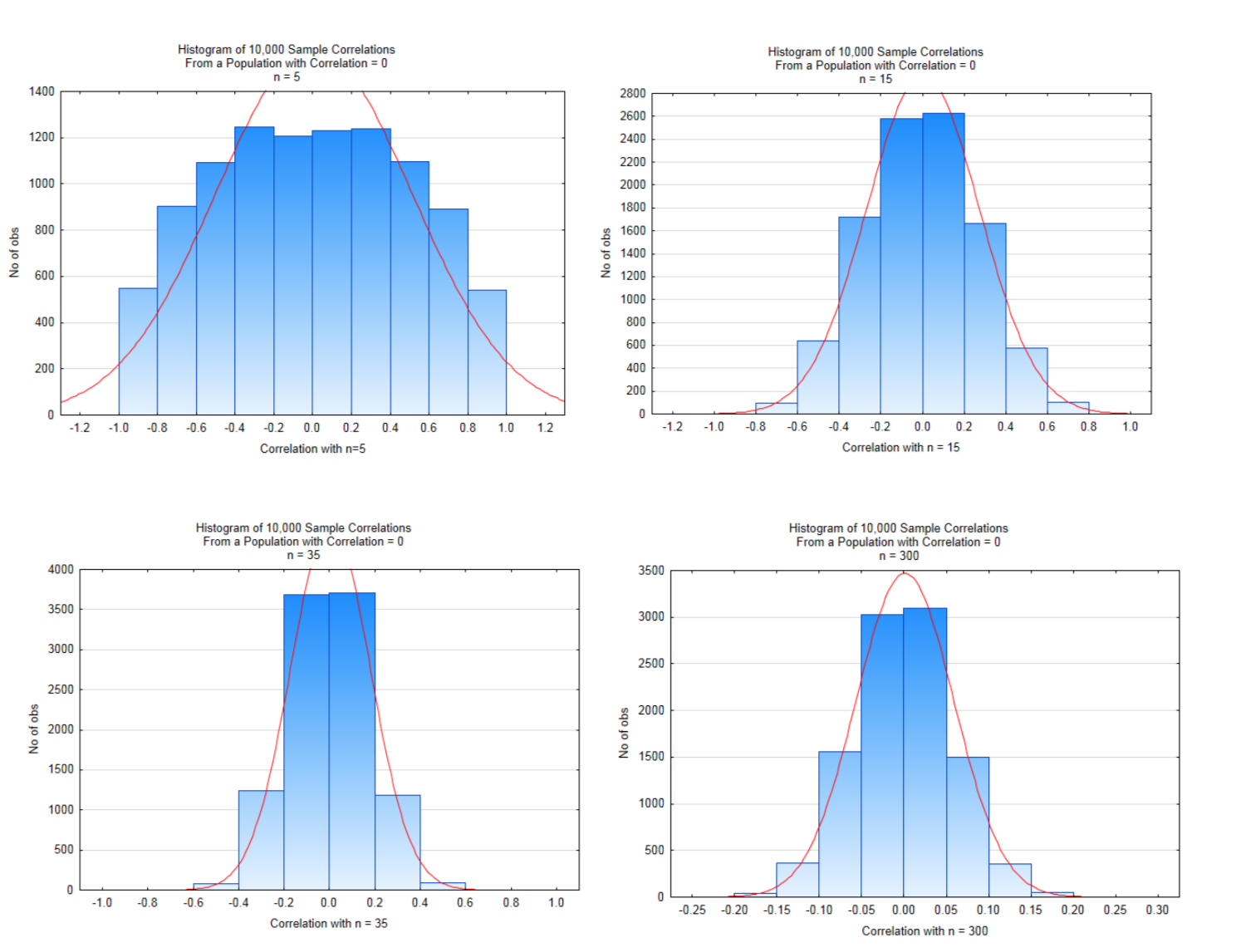
Подивіться уважно на шкали осі х і висоти брусків. Значення поблизу середини графіків є ймовірними значеннями, тоді як значення на крайньому лівому та правому куті графіка є малоймовірними значеннями, які при перевірці гіпотези можуть призвести до значного висновку. При малих розмірах вибірки величина кореляції повинна бути дуже великою, щоб зробити висновок, що існує значна кореляція. Зі збільшенням розміру вибірки величина кореляції може бути набагато меншою, щоб зробити висновок, що існує значна кореляція. Критичні значення для кожного з них наведені в таблиці нижче і засновані на двоххвостовому тесті з рівнем значущості 5%.
| п | 5 | 15 | 35 | 300 |
|---|---|---|---|---|
| т | 2.776 | 2.145 | 2.032 | 1,968 |
| |р| | 0,848 | 0.511 | 0,334 | 0,113 |
У гістограмі в правому нижньому куті, в якій розмір вибірки становив 300, кореляція, яка перевищує 0,113, призведе до висновку значної кореляції, але виникає питання про те, чи є кореляція, яка мала, дуже значущою, навіть якщо вона є значною. Це може бути значущим, а може і ні. Дослідник повинен визначити, що для кожної ситуації.
Повертаючись до аналізу коефіцієнтів Джині та рівня бідності, оскільки між цими двома змінними не було значної кореляції, то немає сенсу намагатися використовувати коефіцієнти Джині для оцінки рівня бідності або зосереджуватися на зміні розриву у багатстві як спосіб покращення рівня бідності. Можуть бути й інші причини бажання змінити розрив у багатстві, але його вплив на рівень бідності, здається, не є однією з причин. З іншого боку, оскільки існує значна кореляція між співвідношенням зайнятості та населення та рівнем бідності, то доцільно використовувати взаємозв'язок між ними як модель оцінки рівня бідності для конкретних коефіцієнтів зайнятості та населення. Якщо цей зв'язок можна визначити як причинно-наслідковий, то це виправдовує поліпшення співвідношення зайнятості та населення, щоб допомогти зменшити рівень бідності. Іншими словами, людям потрібні робочі місця, щоб вийти з бідності.
Оскільки коефіцієнт кореляції моменту Пірсона вимірює силу лінійної залежності між двома змінними, то розумно знайти рівняння лінії, яке найкраще відповідає даним. Ця лінія називається лінією регресії найменших квадратів або лінією найкращого прилягання. До графіку додано лінію регресії для співвідношення зайнятості та населення та рівня бідності. Зверніть увагу, що є негативний нахил до лінії. Це відповідає знаку коефіцієнта кореляції.
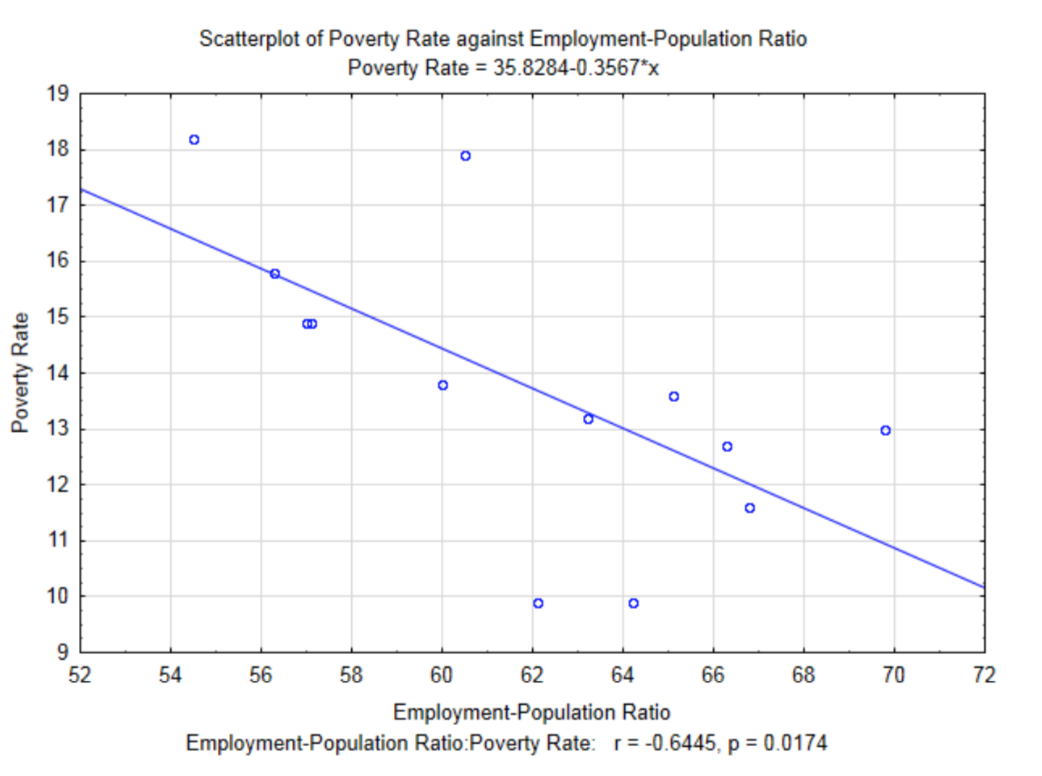
Рівняння лінії, як це видно в підзаголовку графіка\(y = 35.8284 – 0.3567x\), - це, де\(x\) коефіцієнт зайнятості та населення та\(y\) рівень бідності. Будучи студентом алгебри, вас вчили, що лінійне рівняння може бути записано у вигляді\(y = mx + b\). У статистиці рівняння лінійної регресії записуються у формі,\(y = b + mx\) за винятком того, що вони традиційно показані як\(y' = a + bx\) де\(y'\) представляє значення y, передбачене лінією,\(a\) представляє\(y\) перехоплення і\(b\) представляє нахил.
Для розрахунку значень\(a\) і\(b\), спочатку потрібні 5 інших значень. Це кореляція (r), середнє і стандартне відхилення для\(x\) (\(\bar{x}\)і\(s_x\)) і середнє і стандартне відхилення для\(y\) (\(\bar{y}\)і\(s_y\)). Спочатку знайдіть\(b\) за допомогою формули:\(b = r(\dfrac{s_y}{s_x})\). Далі підставляємо\(\bar{y}\)\(\bar{x}\), і\(b\) в основне лінійне рівняння\(\bar{y} = a + b\bar{x}\) і вирішуємо для\(a\).
Для цього прикладу\(r = -0.6445\),\(bar{x} = 61.76\),\(s_x = 4.67\),\(bar{y} = 13.80\), і\(s_y = 2.58\).
\(b = r(\dfrac{s_y}{s_x})\)
\(b = -0.6445(\dfrac{2.58}{4.67}) = -0.3561\)
\(\bar{y} = a + b\bar{x}\)
\(1380 = a + -0.3561(61.76)\)
\(a = 35.79\)
Тому остаточне рівняння регресії є\(y' = 35.79 - 0.3561x\). Різниця між цим рівнянням і тим, що знаходиться на графіку, є результатом похибок округлення, використовуваних для цих розрахунків.
Рівняння регресії дозволяє оцінити значення y, але не дає вказівки на точність оцінки. Іншими словами, який вплив має взаємозв'язок між\(x\) і\(y\) на\(y\) цінність?
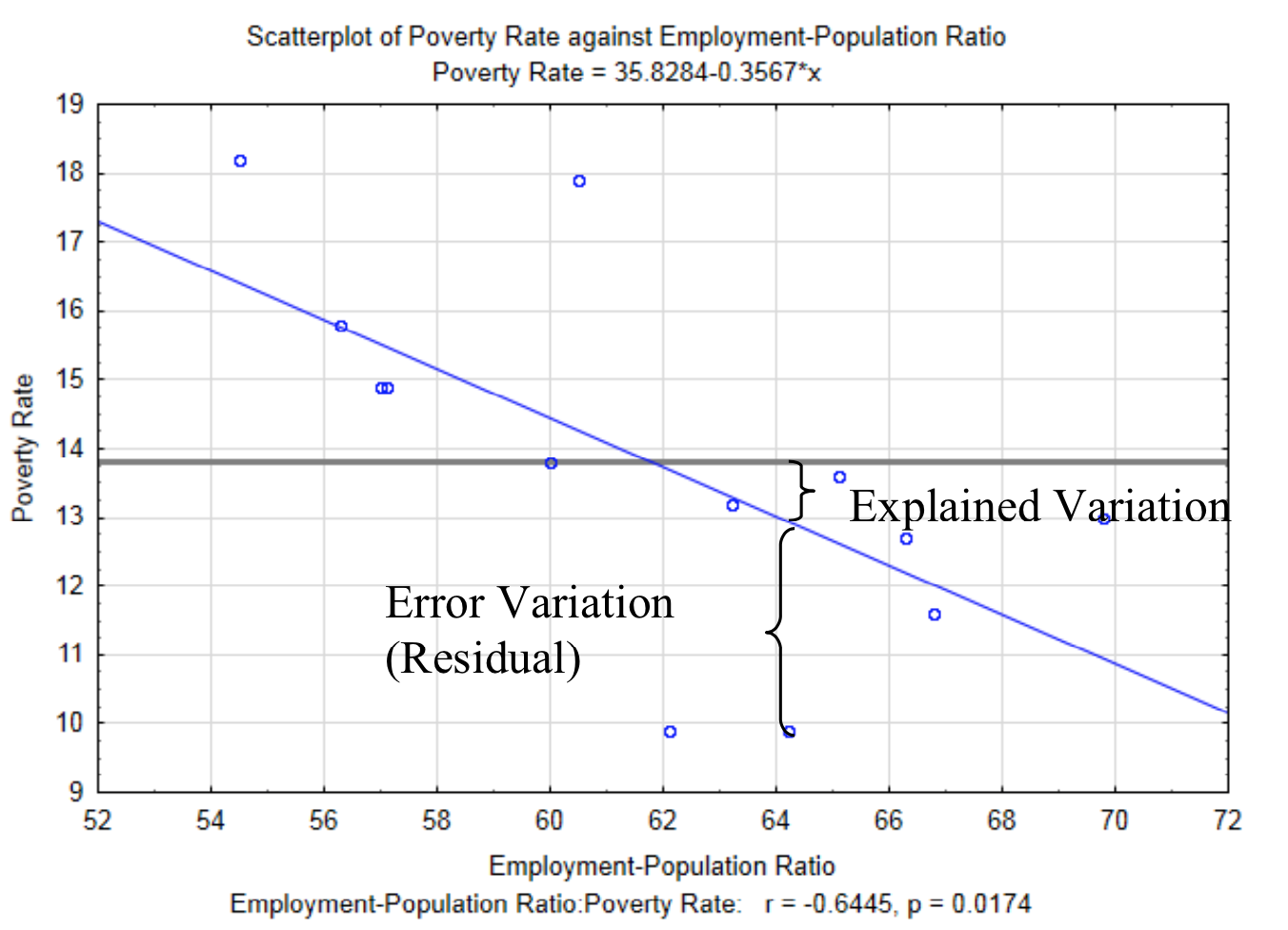
Визначити вплив взаємозв'язку між\(x\) і\(y\) починається з думки про те, що існує варіація між\(y\) значенням і середнім\(y\) значенням всіх значень (\(bar{y}\)). Це те, що ви бачили з одноманітними кількісними даними. Існує дві причини, за якими\(y\) значення не еквівалентні середньому. Вони називаються поясненою варіацією та варіацією помилок. Пояснена варіація - це варіація, яка є наслідком відносин\(y\) з\(x\). Іншими словами,\(y\) не дорівнює середньому всіх\(y\) значень, оскільки співвідношення, показане лінією регресії, впливає на нього. Варіація помилки - це варіація між фактичною точкою та\(y\) значенням, передбаченою лінією регресії, що є наслідком усіх інших факторів, що впливають на випадкову величину відгуку. Ця вертикальна відстань між кожною фактичною точкою даних і\(y\) прогнозованим значенням (\(y'\)) називається залишковою. Пояснена варіація та варіація помилок показані на графіку нижче. Горизонтальна лінія в 13,8 - середнє значення всіх\(y\) значень.
Загальна варіація задається сумою квадратної відстані, кожне значення від середнього\(y\) значення. Це показано як\(\sum_{i = 1}^{n} (y_i - \bar{y})^2\).
Пояснена варіація задається сумою квадратних відстаней,\(y\) значення, передбачене рівнянням регресії (\(y'\)), становить від середнього\(y\) значення,\(\bar{y}\). Це показано як
\[\sum_{i = 1}^{n} (y_i' - \bar{y})^2.\]
Варіація похибки задається сумою квадратних відстаней фактичного значення\(y\) даних від прогнозованого\(y\) значення (\(y'\)). Це показано як\(\sum_{i = 1}^{n} (y_i - y_i ')^2\).
Зв'язок між ними можна показати за допомогою рівняння слова та алгебраїчного рівняння.
Загальна варіація = Пояснена варіація+Помилка варіації
\[\sum_{i = 1}^{n} (y_{i} - \bar{y})^{2} = \sum_{i = 1}^{n} (y_{i}' - \bar{y})^{2} + \sum_{i = 1}^{n} (y_{i} - y_{i} ')^2\]
Основна причина цього обговорення полягає в тому, щоб привести нас до розуміння математичного (хоча і не обов'язково причинного) впливу\(x\) змінної на\(y\) змінну. Оскільки цей вплив є поясненою варіацією, то ми можемо знайти відношення поясненої варіації до загальної варіації. Визначимо це співвідношення як коефіцієнт детермінації. Співвідношення представлено\(r^2\).
\(r^2 = \dfrac{\sum_{i = 1}^{n} (y_i' - \bar{y})^2}{\sum_{i = 1}^{n} (y_i - \bar{y})^2}\)
Коефіцієнт визначення - квадрат коефіцієнта кореляції. Те, що він представляє, - це частка дисперсії однієї змінної, яка виникає внаслідок математичного впливу дисперсії іншої змінної. Коефіцієнт визначення завжди буде значенням між 0 і 1, тобто\(0 \le r^2 \le 1\). Хоча\(r^2\) представлений таким чином, про нього часто говорять у відсотках, що призводить до множення\(r^2\) значення на 100.
У розкидній діаграмі рівня бідності проти співвідношення зайнятості та населення, кореляція є\(r = - 0.6445\), таким чином\(r^2 = 0.4153\). Таким чином, зроблено висновок, що 41,53% впливу на дисперсію рівня бідності припадає на дисперсію в співвідношенні зайнятості та населення. Решта впливу, який вважається варіацією помилок, походить від деяких інших елементів у списку можливих змінних, які можуть вплинути на бідність.
Не існує остаточної шкали для визначення бажаних рівнів для\(r^2\). Хоча значення, близькі до 1, показують сильну математичну залежність, а значення, близькі до 0, показують слабку залежність, дослідник повинен розглядати фактичне\(r^2\) значення значення в контексті своїх досліджень.
Технологія
Обчислення кореляційних та регресійних рівнянь вручну може бути дуже стомлюючим і схильним до помилок округлення. Отже, технологія зазвичай використовується для регресійного аналізу. Тут будуть використані дані, які використовувалися при порівнянні коефіцієнтів Джині з рівнем бідності.
| Коефіцієнт Джині | Рівень бідності |
|---|---|
| 0,486 | 10.1 |
| 0,443 | 9.9 |
| 0,44 | 11.6 |
| 0,433 | 13 |
| 0,419 | 13.2 |
| 0,442 | 14.4 |
| 0,464 | 10.3 |
до 84 Калькулятор
Щоб ввести дані, скористайтеся Stat — Edit — Enter, щоб перейти до списків, які були використані в розділі 4. Очистити списки один і два, перемістивши курсор вгору до рівня L1, натиснувши кнопку очищення, а потім перемістивши курсор вниз. Те ж саме виконайте для L2.
Введіть коефіцієнти Джині в L1, рівень бідності в L2. Вони повинні залишатися парними так само, як вони є в таблиці.
Для визначення значення t, p-значення, значень r і r2 і числових значень у рівнянні регресії використовуйте Stat — Тести — E: LinRegtTest. Введіть Xlist як L1 і Ylist як L2. Альтернативна гіпотеза відображається як\(\beta\) &\(\rho\):\(\ne\) 0. Наведіть курсор на Розрахувати і натисніть Enter.
Вихід такий:
Тест\(\rho \ne 0\)
Лінрегт
\(y = a + bx\)
\(\beta \ne 0\) і т = -1,912582657
р = 0,1140079665
дф = 5
б = -52.72871602
\(s = 1.479381344\) (стандартна помилка)
\(r^2 = 0.4224975727\)
\(r = -0.6499981406\)
Microsoft Excel містить надбудову, яка повинна бути встановлена для завершення регресійного аналізу. У більш свіжих версіях Excel (2010) цей адмін може бути встановлений
- Виберіть вкладку «Файл»
- Виберіть параметри
- У лівій частині виберіть Надбудови
- Внизу, поруч із тим, де написано надбудови Excel, натисніть на Перейти Перевірте перше поле, де написано Analysis ToolPak, а потім натисніть кнопку ОК. На цьому етапі вам може знадобитися ваш диск Excel.
Щоб зробити фактичний аналіз:
- Виберіть вкладку даних
- Виберіть параметр аналізу даних (у верхній правій частині екрана)
- Виберіть «Регресія»
- Заповніть пробіли для діапазонів даних y та x.
- Натисніть ОК.
Буде створено новий аркуш, який містить підсумковий результат. Деякі цифри показані сірим кольором, щоб допомогти вам знати, які числа шукати. Зверніть увагу, як вони відповідають виводу з ТІ 84 і розрахунків, зроблених раніше в цьому розділі.