7.3: Вирішення проблем

Last updated

Oct 27, 2022
Save as PDF
- 7.2: Мова
- 7.4: Що таке інтелект і творчість?

Rose M. Spielman, William J. Jenkins, Marilyn D. Lovett, et al.
OpenStax

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

Цілі навчання

Опишіть стратегії вирішення проблем
Визначте алгоритм і евристику
Поясніть деякі загальні перешкоди для ефективного вирішення проблем та прийняття рішень

Люди стикаються з проблемами щодня - як правило, кілька проблем протягом дня. Іноді ці проблеми прості: щоб подвоїти рецепт тіста для піци, наприклад, все, що потрібно, це щоб кожен інгредієнт в рецепті був подвоєний. Іноді, однак, проблеми, з якими ми стикаємося, є більш складними. Наприклад, скажімо, у вас є термін роботи, і ви повинні надіслати друковану копію звіту своєму керівнику до кінця робочого дня. Звіт чутливий до часу і повинен бути відправлений протягом ночі. Ви закінчили звіт минулої ночі, але ваш принтер не працюватиме сьогодні. Що робити? Спочатку потрібно виявити проблему, а потім застосувати стратегію вирішення проблеми.

Стратегії вирішення проблем

Коли перед вами виникає проблема - чи це складна математична задача або зламаний принтер, як ви її вирішуєте? Перш ніж знайти рішення проблеми, спочатку необхідно чітко визначити проблему. Після цього можна застосувати одну з багатьох стратегій вирішення проблем, сподіваємось, що це призведе до вирішення.

Стратегія вирішення проблем - це план дій, який використовується для пошуку рішення. Різні стратегії мають різні плани дій, пов'язані з ними (табл. 7.2). Наприклад, відома стратегія - проби і помилки. Стара приказка «Якщо спочатку у вас не виходить, спробуйте, спробуйте ще раз» описує спроби і помилки. Що стосується вашого зламаного принтера, ви можете спробувати перевірити рівень чорнила, і якщо це не працює, ви можете перевірити, чи не застряг лотка для паперу. Або, можливо, принтер насправді не підключений до вашого ноутбука. Використовуючи метод проб і помилок, ви продовжуєте пробувати різні рішення, поки не вирішите свою проблему. Хоча проби та помилки, як правило, не є однією з найбільш ефективних у часі стратегій, вона є загальноприйнятою.

Стратегії вирішення проблем
Метод	Опис	Приклад
Проби і помилки	Продовжуйте пробувати різні рішення, поки проблема не буде вирішена	Перезавантаження телефону, відключення WiFi, відключення блютуз для того, щоб визначити, чому ваш телефон несправний
Алгоритм	Покрокова формула вирішення проблем	Інструкція по установці нового програмного забезпечення на комп'ютер
Евристичний	Загальний фреймворк вирішення проблем	Робота в зворотному напрямку; розбивання завдання на кроки

Таблиця 7.2

Ще один вид стратегії - алгоритм. Алгоритм - це формула вирішення проблем, яка надає вам покрокові інструкції, що використовуються для досягнення бажаного результату (Kahneman, 2011). Ви можете придумати алгоритм як рецепт з дуже докладними інструкціями, які дають однаковий результат кожного разу, коли вони виконуються. Алгоритми часто використовуються в нашому повсякденному житті, особливо в інформатиці. Коли ви запускаєте пошук в Інтернеті, пошукові системи, такі як Google, використовують алгоритми, щоб вирішити, які записи з'являться першими у вашому списку результатів. Facebook також використовує алгоритми, щоб вирішити, які публікації відображати у вашій стрічці новин. Чи можете ви визначити інші ситуації, в яких використовуються алгоритми?

Евристика - це ще один тип стратегії вирішення проблем. Хоча алгоритм повинен точно дотримуватися, щоб отримати правильний результат, евристика - це загальна структура вирішення проблем (Tversky & Kahneman, 1974). Ви можете думати про них як про психічні ярлики, які використовуються для вирішення проблем. «Емпіричне правило» - приклад евристики. Таке правило економить час і сили людини при прийнятті рішення, але незважаючи на свої економічні характеристики, не завжди є найкращим методом для прийняття раціонального рішення. Різні види евристики використовуються в різних типах ситуацій, але імпульс до використання евристики виникає при дотриманні однієї з п'яти умов (Pratkanis, 1989):

Коли людина стикається з занадто великою кількістю інформації
Коли час на прийняття рішення обмежений
Коли рішення, яке потрібно прийняти, неважливо
Коли є доступ до дуже мало інформації для використання при прийнятті рішення
Коли в той же момент приходить на розум відповідна евристика

Робота назад - корисна евристика, в якій ви починаєте вирішувати проблему, зосереджуючись на кінцевому результаті. Розглянемо цей приклад: Ви живете у Вашингтоні, округ Колумбія, і вас запросили на весілля о 16:00 в суботу у Філадельфії. Знаючи, що Interstate 95 має тенденцію до резервного копіювання в будь-який день тижня, вам потрібно відповідно спланувати свій маршрут і час відправлення. Якщо ви хочете бути на весільній службі до 15:30 вечора, а щоб дістатися до Філадельфії без трафіку потрібно 2,5 години, о котрій годині ви повинні вийти з дому? Ви використовуєте робочу назад евристику, щоб планувати події вашого дня на регулярній основі, ймовірно, навіть не думаючи про це.

Ще однією корисною евристикою є практика досягнення великої мети або завдання, розбиваючи її на низку менших кроків. Студенти часто використовують цей поширений метод для завершення великого дослідницького проекту або довгого есе для школи. Наприклад, студенти зазвичай проводять мозковий штурм, розробляють дипломну роботу або основну тему, досліджують обрану тему, організовують свою інформацію в контур, пишуть приблизний чернетку, переглядають та редагують чорновий проект, розробляють остаточний проект, організовують список літератури та коректують свою роботу перед включенням у проект. Велике завдання стає менш переважною, коли вона розбита на ряд невеликих кроків.

ПОВСЯКДЕННЕ З'ЄДНАННЯ: Рішення головоломки

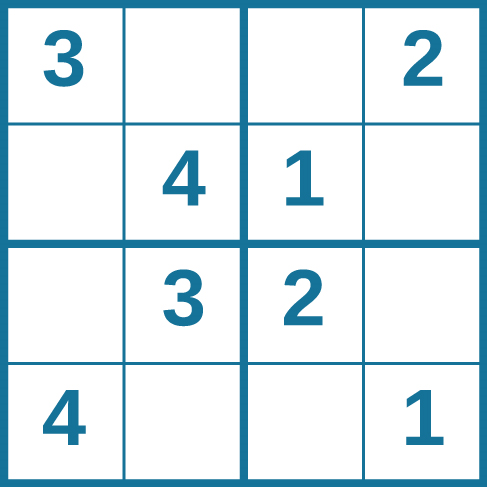
Здатності вирішення проблем можуть покращитися з практикою. Багато людей щодня кидають собі виклик головоломкам та іншим розумовим вправам, щоб відточити свої навички вирішення проблем. Пазли судоку з'являються щодня в більшості газет. Як правило, головоломка судоку являє собою сітку 9 × 9. Просте судоку нижче (рис. 7.7) - це сітка 4 × 4. Щоб вирішити головоломку, заповніть порожні поля однією цифрою: 1, 2, 3 або 4. Ось правила: Числа повинні становити 10 у кожному виділеному жирному полі, кожному рядку та кожному стовпці; однак кожна цифра може відображатися лише один раз у полі, виділеному жирним шрифтом, рядку та стовпці. Час себе, як ви вирішите цю головоломку і порівняйте свій час з однокласником.

Показується головоломка Судоку з чотирьох стовпців на чотири рядки. У верхній лівій клітинці міститься цифра 3. У верхній правій клітинці міститься цифра 2. У нижній правій клітинці міститься цифра 1. У нижній лівій клітинці міститься цифра 4. Клітинка на перетині другого рядка і другого стовпця містить цифру 4. Клітинка праворуч від неї містить цифру 1. Клітинка під осередком, що містить цифру 1, містить цифру 2. Клітинка зліва від осередку, що містить цифру 2, містить цифру 3. — Малюнок **7.7** Скільки часу вам знадобилося, щоб вирішити цю головоломку судоку? (Відповідь ви можете побачити в кінці цього розділу.)

Ось ще один популярний тип головоломки (рис. 7.8), який кидає виклик вашим навичкам просторового міркування. З'єднайте всі дев'ять точок чотирма сполучними прямими лініями, не відриваючи олівець від паперу:

Контур квадратної форми містить три ряди і три стовпчики точок з рівним простором між ними. — Малюнок $\PageIndex{2}$ : Ви це зрозуміли? (Відповідь знаходиться в кінці цього розділу.) Як тільки ви зрозумієте, як зламати цю головоломку, ви не забудете.

Погляньте на логічну головоломку «Puzzling Scales» нижче (рис. 7.9). Сем Лойд, відомий майстер головоломки, створив і вдосконалював незліченні головоломки протягом усього свого життя (Cyclopedia of Puzzles, nd.).

Показана головоломка за участю масштабу. У верхній частині малюнка написано: «Сем Лойдс загадкові ваги». Перший ряд головоломки показує збалансовану шкалу з 3 блоками і зверху зліва і 12 кульок праворуч. Нижче цього рядка написано: «Так як ваги тепер балансують». Наступний ряд головоломки показує збалансовану шкалу з тільки зверху зліва, і 1 блок і 8 кульок праворуч. Нижче цього рядка написано: «І баланс, коли влаштований таким чином». Третій ряд показує незбалансовану шкалу з вершиною на лівій стороні, яка набагато нижче правого боку. Права сторона порожня. Під цим рядком він читає: «Тоді скільки мармуру потрібно буде збалансувати з цією вершиною?» — Малюнок **7.9** Які кроки ви зробили, щоб вирішити цю головоломку? Ви можете прочитати рішення в кінці цього розділу.

Підводні камені для вирішення проблем

Однак не всі проблеми успішно вирішуються. Які виклики заважають нам успішно вирішити проблему? Альберт Ейнштейн одного разу сказав: «Божевілля робить те ж саме знову і знову і очікує іншого результату». Уявіть собі людину в кімнаті, яка має чотири дверних прорізи. Один дверний отвір, який завжди був відкритий в минулому, тепер заблокований. Людина, яка звикла виходити з кімнати за цим конкретним дверним отвором, продовжує намагатися вийти через той самий дверний отвір, хоча інші три дверні прорізи відкриті. Людина застрягла - але їй просто потрібно піти до іншого дверного отвору, замість того, щоб намагатися вийти через замкнений отвір. Психічний набір - це те, де ви наполегливо наближаєтесь до проблеми таким чином, який працював у минулому, але явно не працює зараз.

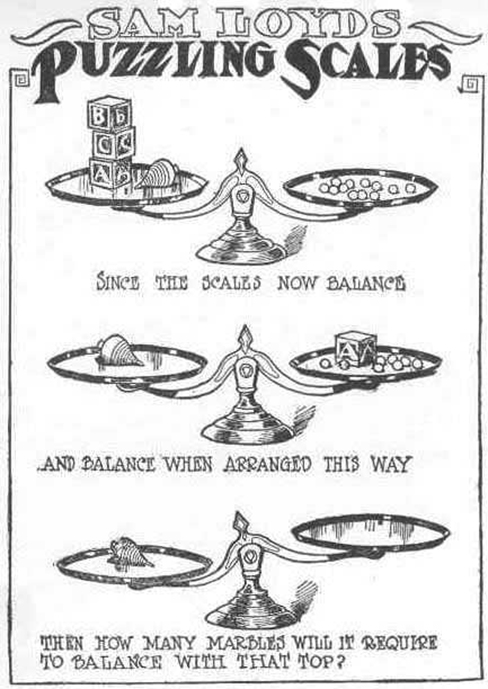
Функціональна фіксованість - це тип ментального набору, де ви не можете сприймати об'єкт, який використовується для чогось іншого, ніж те, для чого він був розроблений. Данкер (1945) проводив фундаментальні дослідження функціональної фіксації. Він створив експеримент, в якому учасникам дарували свічку, книгу сірників і коробку мініатюр. Їм було доручено використовувати ці предмети, щоб прикріпити свічку до стіни, щоб вона не капала віск на таблицю нижче. Учасникам довелося використовувати функціональну фіксацію для вирішення проблеми (рис. 7.10). Під час місії «Аполлона-13» на Місяць інженерам НАСА з управління місіями довелося подолати функціональну фіксованість, щоб врятувати життя астронавтів на борту космічного корабля. Вибух в модулі космічного корабля пошкодив кілька систем. Космонавтам загрожувало отруєння підвищенням рівня вуглекислого газу через проблеми з фільтрами вуглекислого газу. Інженери знайшли спосіб для космонавтів використовувати запасні поліетиленові пакети, стрічку та повітряні шланги для створення імпровізованого повітряного фільтра, який врятував життя космонавтів.

На малюнку а показана книга сірників, коробка мініатюр і свічка. На малюнку б зображена свічка, що стоїть в коробці, яка тримала мініатюри. Thumbtack прикріплює коробку, яка утримує свічку до стіни. — Малюнок **7.10** У класичному дослідженні Данкера учасникам надали три об'єкти у верхній панелі та попросили вирішити проблему. Розчин показаний в нижній частині.

Посилання на навчання

Ознайомтеся з цією сценою Apollo 13 про інженерів NASA, які долають функціональну фіксованість, щоб дізнатися більше.

Дослідники дослідили, чи впливає культура на функціональну фіксацію. В одному експерименті осіб з групи Шуар в Еквадорі було запропоновано використовувати об'єкт з метою, відмінною від тієї, для якої спочатку призначався об'єкт. Наприклад, учасникам розповіли історію про ведмедя і кролика, які були розділені річкою і попросили вибрати серед різних предметів, включаючи ложку, чашку, гумки і так далі, щоб допомогти тваринам. Ложка була єдиним об'єктом досить довго, щоб охопити уявну річку, але якщо ложка була представлена таким чином, що відображає її нормальне використання, учасникам знадобилося більше часу, щоб вибрати ложку, щоб вирішити проблему. (Німецький & Барретт, 2005). Дослідники хотіли знати, чи впливає вплив вузькоспеціалізованих інструментів, як це відбувається з особами в промислово розвинених країнах, на їх здатність подолати функціональну фіксованість. Визначено, що функціональна фіксація спостерігається як у промислово розвинених, так і в неіндустріалізованих культурах (German & Barrett, 2005).

Для того, щоб приймати правильні рішення, ми використовуємо наші знання і свої міркування. Найчастіше ці знання і міркування є здоровими і твердими. Іноді, однак, нас коливають упередження або інші маніпулюють ситуацією. Наприклад, припустимо, ви з трьома друзями хотіли зняти будинок і мали об'єднаний цільовий бюджет 1600 доларів. Ріелтор показує вам тільки дуже запущені будинки за $1,600, а потім показує вам дуже хороший будинок за $2,000. Чи можете ви попросити кожну людину заплатити більше в оренду, щоб отримати $2,000 додому? Чому ріелтор покаже вам запущені будинки і гарний будинок? Ріелтор може оскаржувати ваш упередження якоря. Упередження прив'язки виникає, коли ви зосереджуєтесь на одній частині інформації при прийнятті рішення або вирішенні проблеми. У цьому випадку ви настільки зосереджені на кількості грошей, які ви готові витратити, що ви можете не визнати, які види будинків доступні в цій ціновій точці.

Підтвердженням упередженості є тенденція зосереджуватися на інформації, яка підтверджує ваші існуючі переконання. Наприклад, якщо ви вважаєте, що ваш професор не дуже приємний, ви помічаєте всі випадки грубої поведінки, виставлені професором, ігноруючи незліченні приємні взаємодії, в яких він бере участь щодня. Упередженість заднім числом змушує вас повірити, що подія, яку ви щойно пережили, була передбачуваною, хоча це дійсно не було Іншими словами, ви знали, що все вийде так, як вони це зробили. Представницька упередженість описує несправний спосіб мислення, при якому ви ненавмисно стереотипуєте когось або щось; наприклад, ви можете припустити, що ваші професори проводять вільний час, читаючи книги і займаючись інтелектуальною бесідою, тому що ідея про те, щоб вони проводили свій час, граючи волейбол або відвідування парку розваг не вписується в ваші стереотипи професорів.

Нарешті, евристика доступності - це евристика, в якій ви приймаєте рішення на основі прикладу, інформації або недавнього досвіду, який є доступним для вас, хоча це може бути не найкращим прикладом для інформування вашого рішення. Упередженості, як правило, «зберігають те, що вже встановлено - підтримувати наші раніше існуючі знання, переконання, ставлення та гіпотези» (Aronson, 1995; Kahneman, 2011). Ці упередження зведені в табл. 7.3.

Резюме упередженості рішень
Упередженість	Опис
Анкерний	Тенденція зосереджуватися на одній конкретній частині інформації при прийнятті рішень або вирішенні проблем
Підтвердження	Орієнтується на інформацію, яка підтверджує існуючі переконання
заднім числом	Віра в те, що подія просто пережила, була передбачуваною
Представник	Ненавмисне стереотипування когось чи чогось
Наявність	Рішення ґрунтується або на наявному прецеденті, або на прикладі, який може бути несправним

Таблиця 7.3

Посилання на навчання

Перегляньте це музичне відео, створене вчителями про когнітивні упередження, щоб дізнатися більше.

Чи змогли ви визначити, скільки мармуру потрібно, щоб збалансувати ваги на малюнку 7.9? Вам потрібно дев'ять. Чи змогли ви вирішити проблеми на малюнку 7.7 та рисунку 7.8? Ось відповіді (рис. 7.11).

Малюнок 7.11