14: Послідовність
- Last updated
- Save as PDF
- Page ID
- 82012
Ми розглянули три окремі проблеми оптимізації в нашому дослідженні ідеально конкурентоспроможної (ПК) фірми. Рисунки 14.1, 14.2 та 14.3 дають знімок початкового рішення та ключовий порівняльний статичний аналіз кожної з трьох задач оптимізації.
Ця глава пов'язує речі разом з фундаментальним моментом, що ці три проблеми тісно інтегровані і насправді є різними поглядами однієї фірми і однаковим оптимальним рішенням. Змініть екзогенну змінну, і всі три проблеми оптимізації зачіпаються. Нові оптимальні рішення та результати порівняльної статики є послідовними, тобто вони говорять вам одне і те ж і ніколи не суперечливі.
На малюнку 14.1 показана проблема мінімізації витрат на стороні введення. Кількість є екзогенною у цій проблемі, і фірма шукає вхідну суміш, яка мінімізує загальну вартість виробництва даного q.
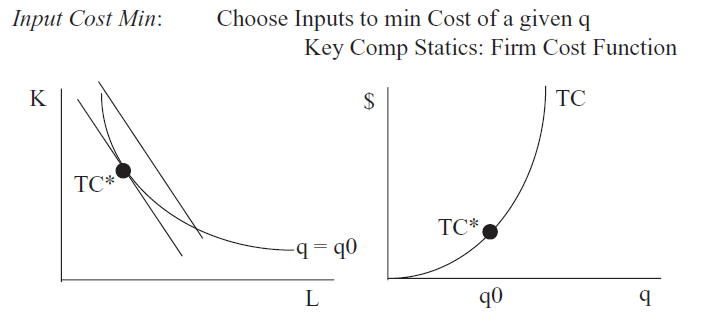 Малюнок 14.1: Мінімізація початкових витрат та функція витрат.
Малюнок 14.1: Мінімізація початкових витрат та функція витрат.На правій панелі на малюнку 14.1 показана функція витрат, яка походить від відстеження мінімальної загальної вартості, як q варіюється, або рівно.
На малюнку 14.2 показано максимізацію прибутку на вихідній стороні. Фірма ПК (оскільки\(P=MR\) є горизонтальною лінією) отримує середні та граничні криві витрат від функції витрат та знаходить кількість, яка максимізує прибуток.
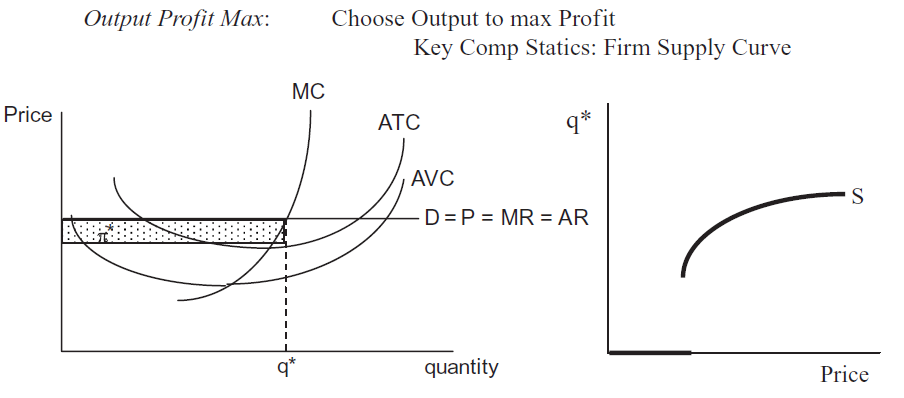 Малюнок 14.2: Максимізація початкового прибутку та крива пропозиції.
Малюнок 14.2: Максимізація початкового прибутку та крива пропозиції.На правій панелі на малюнку 14.2 показано, звідки походять криві живлення: шок P, за інших рівних сторін, і трек оптимального q.
Малюнок 14.3 повертається до вхідної сторони, але на цей раз фірма вирішує проблему максимізації прибутку, вибираючи, скільки робочої сили найняти.
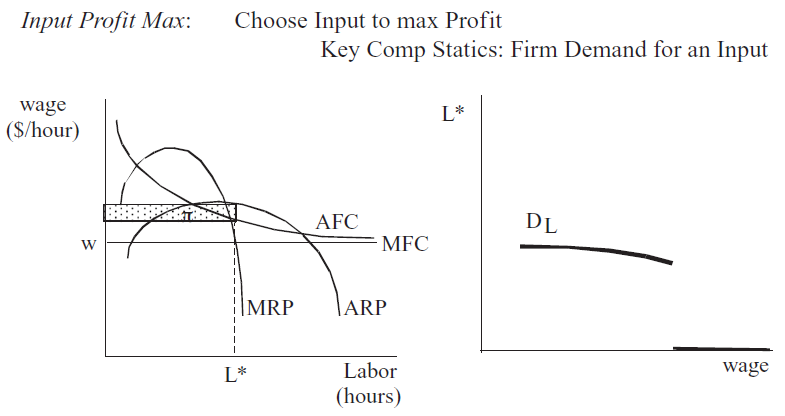 Малюнок 14.3: Початкова максимізація прибутку і попит на робочу силу.
Малюнок 14.3: Початкова максимізація прибутку і попит на робочу силу.На правій панелі в 14.3 показано, як зміна w, за інших рівних сторін, виробляє криву попиту на робочу силу.
Ці три проблеми оптимізації мають спільну методологію. У кожному конкретному випадку ми налаштовуємо і вирішуємо задачу, потім робимо порівняльний статичний аналіз. Є й інші потрясіння, які можна дослідити, але показаний тут є найважливішим.
Але є одна остання важлива концепція, яка знаходиться в центрі уваги цієї глави: ці три проблеми не існують ізольовано, натомість вони сплетені разом, щоб скласти Теорію фірми. Відносини між трьома демонструють послідовність, яку можна продемонструвати за допомогою Excel.
Ідеальна конкуренція в довгостроковій перспективі
КРОК Відкрийте книгу Excel Consistency.xls і прочитайте Введення аркуша; потім перейдіть до теорії фірми LongRun аркуша. Використовуйте кнопку, щоб підігнати графіки на екрані, щоб усі їх можна було побачити одночасно.
кнопку, щоб підігнати графіки на екрані, щоб усі їх можна було побачити одночасно.
Перший і найважливіший момент полягає в тому, що всі три проблеми оптимізації, в унісон, складають Теорію фірми. Можливо, тому, що вони бачать це у вступній економіці, багато студентів думають про графік максимізації прибутку на виході як про фірму. Дисплей в Consistency.xls дає сильну візуальну презентацію і постійне нагадування про те, що фірма має три грані.
Сірий фон осередки мертві (натисніть на одну, щоб побачити, що вона має число, а не формулу). Вони служать орієнтирами для порівнянь, коли ми робимо порівняльну статику.
Графіки максимізації вихідного та вхідного прибутку не мають звичних U-образних кривих, оскільки виробничою функцією є Кобб-Дуглас. Ця функціональна форма не може генерувати звичайні U-подібні криві MC та змінного струму (або перевернуті U-образні MRP та ARP). Немає окремої кривої AVC, тому що ми знаходимося в довгостроковій перспективі, так що\(AC = AVC\).
КРОК Порівняйте початкові рішення для кожної з трьох проблем.
Є кілька способів, за якими вони погоджуються.
-
\(L \mbox{*}\)і\(K \mbox{*}\) однакові на графіках вхідного прибутку Max (зліва) та вхідних витрат Min (середній).
-
Якщо ви використовуєте ці суми L і K, ви отримаєте 636 одиниць продукції, як показано на графіку Output Profit Max (праворуч).
-
\(\pi \mbox{*}\)однаковий у графіках вхідного та вихідного прибутку Макс. У графіку вхідних витрат Min немає прибутку, оскільки немає вихідної ціни (P) і, отже, немає доходу в цій задачі оптимізації.
-
Загальна вартість з кожного боку абсолютно однакова. Ви можете знайти TC з Input Profit Max, створивши комірку, яка обчислює\(wL \mbox{*} + rK \mbox{*}\). Це дорівнюватиме $36,262. З боку Output Profit Max обчислити TC, віднімаючи дохід\(Pq\), з прибутку. Знову ж таки, ви отримуєте $36,262.
Ми також можемо побачити послідовність у способах, якими три проблеми оптимізації реагують на потрясіння. Як і слід було очікувати, результати порівняльної статики ідентичні.
КРОК Підвищення заробітної плати на 1%. Змініть комірку B2 на 20.2. Використовуйте кнопку, якщо потрібно, щоб чіткіше побачити, як змінилися графіки.
На малюнку 14.4 показані результати.
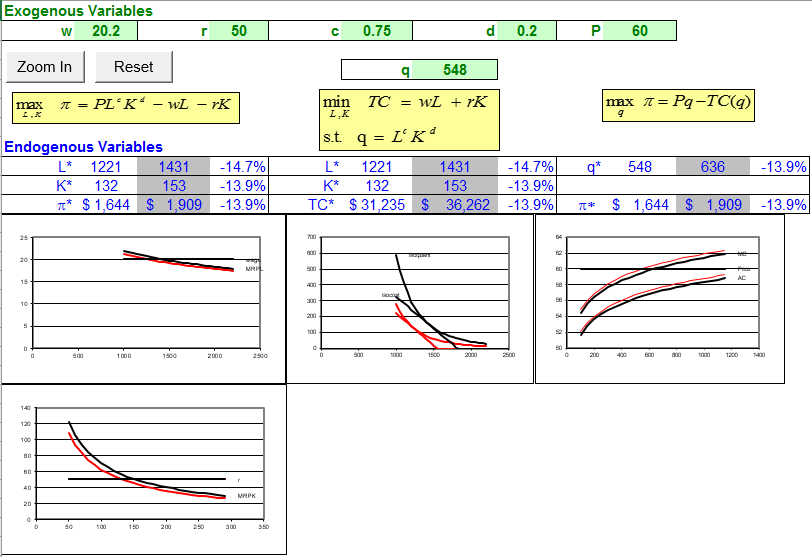
Малюнок 14.4: Шок заробітної плати в довгостроковій перспективі.
Джерело: Consistency.xls! Теорія фірми Long Run
На графіку Input Profit Max ми бачимо, що оптимальне використання робочої сили знизилося на 14,7%, оскільки заробітна плата зросла на 1% (отже, еластичність заробітної плати праці від заробітної плати = $20/год до $20,20/год\(-14.7\)). Попит на робочу силу впав через те, що горизонтальна лінія заробітної плати змістилася вгору і тому, що графік MRP змістився Останній ефект обумовлений тим, що оптимальний К впав.
На графіку Input Cost Min ми бачимо, що фірма мінімізує витрати на виробництво більш низького рівня випуску продукції. Іншими словами, ми знаходимося на новому ізокванті. Зверніть увагу, що зміни\(L \mbox{*}\) і\(K \mbox{*}\) узгоджуються зі зменшенням, повідомленим з результатів Input Profit Max.
Збільшення заробітної плати на графіку Max Output Profit відчувається через зміщення кривих витрат вгору. Фірма зменшується\(q \mbox{*}\) через те, що МК зміщується вгору і тому перетин МР і МК відбувається зліва від початкового рішення.
Рисунок 14.4 і ваш екран показує, як теорія фірми послідовно реагує на шок заробітної плати. Чи вірно це з іншими потрясіннями? Так. Ось ще один приклад.
КРОК Натисніть кнопку, а потім реалізуйте підвищення продуктивності праці до 0.751 шляхом зміни осередку F2.
кнопку, а потім реалізуйте підвищення продуктивності праці до 0.751 шляхом зміни осередку F2.
На малюнку 14.5 показані драматичні результати цього шоку. Використання вхідних даних та вироблений обсяг виробництва збільшився приблизно на 18% у відповідь на цю крихітну зміну в с.
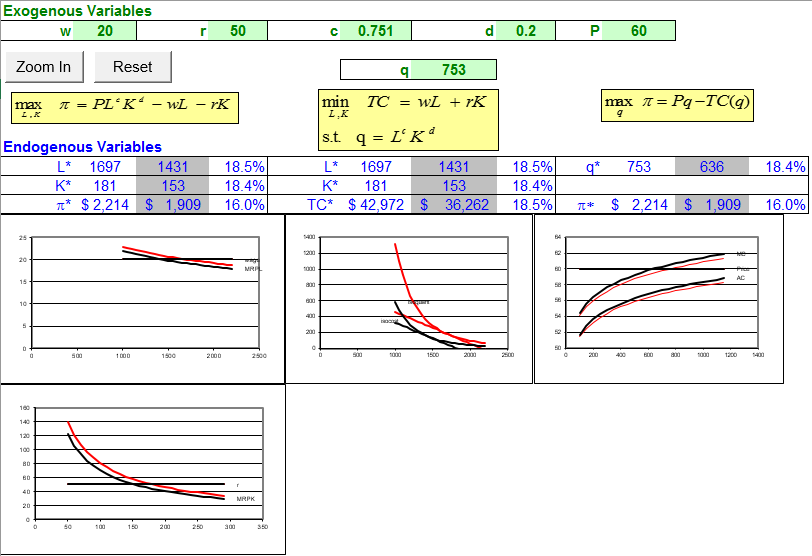
Малюнок 14.5: Шок продуктивності праці в довгостроковій перспективі.
Джерело: Consistency.xls! Теорія фірми Long Run
Як і у випадку з шоком заробітної плати, порівняння наслідків зміни c на три задачі оптимізації показує послідовність. Дві проблеми на стороні входу показують, що використання вхідних даних однакове, і використовувані входи зроблять бажаний вихід на стороні виходу. Прибутки на вхідній і вихідній сторонам однакові. Збільшення продуктивності змістило MRP вгору, а криві витрат вниз.
Інші потрясіння вивчаються в питаннях Q&A та вправ. У кожному випадку, зміна екзогенної змінної, в деяких випадках, виробляє ефекти відчуваються протягом трьох проблем оптимізації, і результати завжди узгоджуються.
Ідеальна конкуренція в короткостроковій перспективі
КРОК Перейти до theoryoftheFirmShortrun аркуша, щоб вивчити порівняльні статичні властивості трьох задач оптимізації в короткостроковій перспективі.
Цей аркуш має кілька відмінностей порівняно з попереднім загальним видом фірми в довгостроковій перспективі.
-
Існує додаткова екзогенна змінна, K, тому що ми знаходимося в короткостроковій перспективі. Його значення встановлюється на довгострокове оптимальне рішення для початкових значень інших параметрів.
-
У задачі макс вхідного прибутку відсутній графік. При фіксованому K нам більше не потрібно зображувати його оптимальне рішення.
-
Існує пряма, горизонтальна лінія в ізоквантному бічному графіку. З фіксованим K фірма не зможе котитися навколо ізокванта, щоб знайти суміш введення, що мінімізує витрати. Він повинен використовувати задану кількість K.
-
У графіку максимального прибутку на виході є крива додаткових витрат. Наявність K фіксованих означає, що існує фіксована вартість, тому тепер ми маємо окремі середні загальні та середні змінні витрати.
КРОК Порівняйте початкові рішення для кожної з трьох проблем. Як і очікувалося, вони погоджуються у використанні вхідних даних, виробленому виході та отриманому прибутку.
Як і раніше, ми можемо змінити світло-зелений фон екзогенних змінних осередків у рядку 2 і стежити за результатами на графіках.
КРОК Застосуйте підвищення заробітної плати на 1%. Змініть комірку B2 на 20.2. Використовуйте кнопку, якщо потрібно, щоб чіткіше побачити, як змінилися графіки.
кнопку, якщо потрібно, щоб чіткіше побачити, як змінилися графіки.
На малюнку 14.6 показані результати цього шоку.
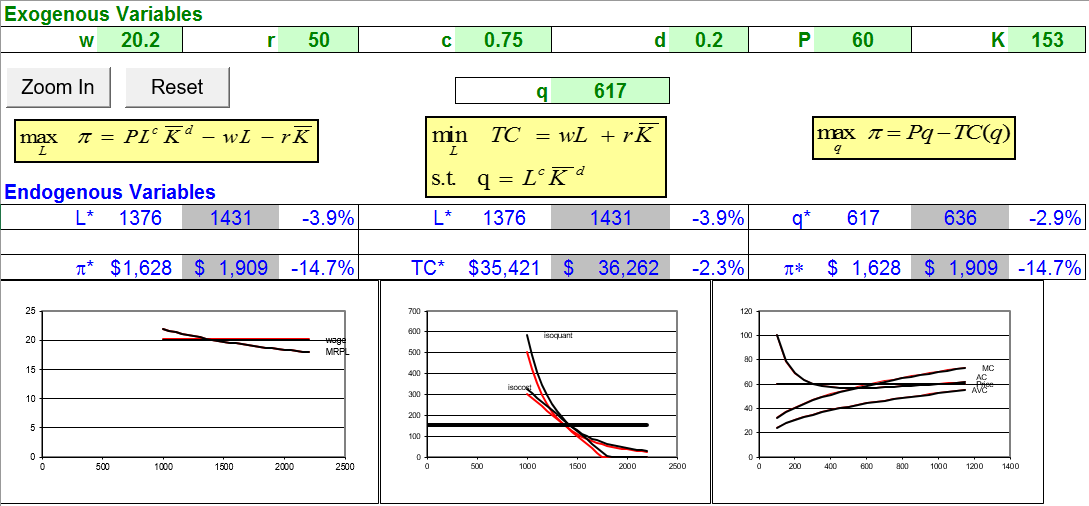
Малюнок 14.6: Шок заробітної плати в короткостроковій перспективі.
Джерело: Consistency.xls! Теорія фірм «Короткий біг»
Звичайні властивості консистенції легко очевидні. Ми спостерігаємо однакові зміни як в\(L \mbox{*}\)\(q \mbox{*}\), так і\(\pi \mbox{*}\) по всій дошці. Зверніть увагу, що максимальна проблема вхідного прибутку не показує зсуву в MRP, оскільки K фіксована.
Якщо порівняти коротке (рис. 14.4) з довгостроковою перспективою (рис. 14.6), то побачимо, що чуйність змін ендогенних змінних більша в довгостроковій перспективі. У довгостроковій перспективі робоча сила та продуктивність падають більше. Прибуток, однак, падає менше в довгостроковій перспективі.
КРОК Натисніть кнопку, а потім реалізуйте підвищення продуктивності праці до 0.751 шляхом зміни осередку F2.
кнопку, а потім реалізуйте підвищення продуктивності праці до 0.751 шляхом зміни осередку F2.
На малюнку 14.7 відображаються результати.
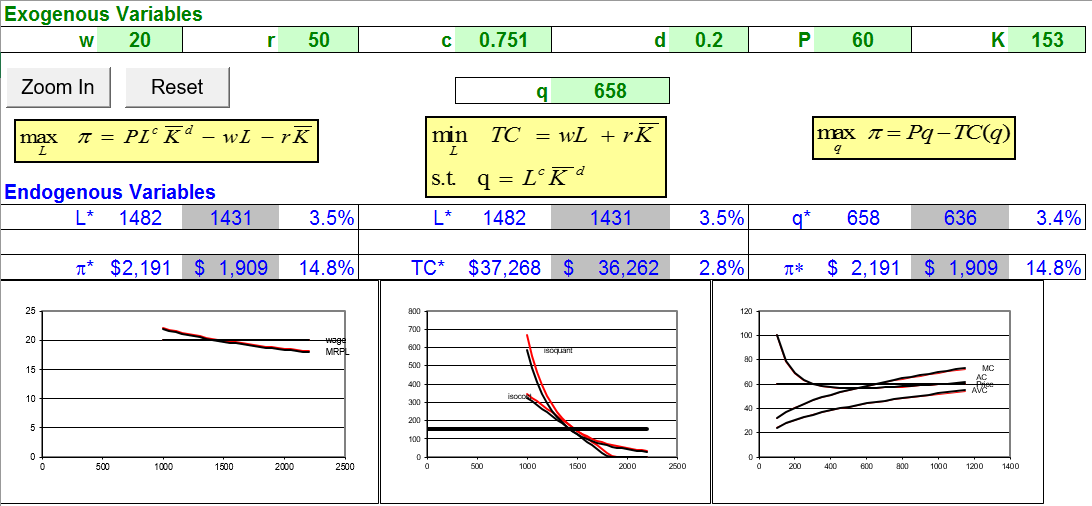
Малюнок 14.7: Шок продуктивності праці в короткостроковій перспективі.
Джерело: Consistency.xls! Теорія фірм «Короткий біг»
Рисунок 14.7 показує послідовність результатів, і, знову ж таки, довгострокові зміни є більш чуйними, ніж у короткостроковій перспективі. L і K падають більше, а збільшення прибутку в довгостроковій перспективі вище.
Довгий проти короткого пробігу
Коли ми порівнювали короткострокові та довгострокові результати шоків у w та c, довгострокова перспектива демонструвала більшу чуйність у праці та виробництві. Чи є загальний принцип в роботі?
Так. Загальний закон полягає в тому, що довгострокові відповіді завжди принаймні як або більш еластичні, ніж у короткостроковій перспективі. Це відоме як принцип Ле Шательє.
Ідея Ле Шательє, яку він спочатку застосував до концепції рівноваги в хімічних реакціях, була введена в економіку нобелівським лауреатом Полом Самуельсоном в 1947 році.
Принцип Ле Шательє пояснює, як система, яка знаходиться в рівновазі, буде реагувати на збурень. Він передбачає, що система буде реагувати таким чином, що буде протидіяти збуренню. Самуельсон, слідуючи методам жорстких наук, транспортував цей принцип хіміка Анрі-Луї Ле Шательє в економіку, щоб вивчити реакцію агентів на зміни цін з огляду на деякі додаткові обмеження. У своєму розширенні цього принципу Самуельсон використовує метафору стиснення повітряної кулі для подальшого пояснення концепції. Якщо ви вичавлюєте балон, його обсяг зменшиться більше, якщо ви будете підтримувати його температуру постійною, ніж вона буде, якщо ви дозволите вичавлювати розігріти його. Цей принцип зараз розглядається як стандартний інструмент для порівняльного статичного аналізу в економічній теорії. (Сенберг та ін., 2005, стор. 51, виноску опущено)
У контексті короткострокових і довгострокових відповідей на потрясіння фірми, принцип Le Chatelier говорить, що довгострокові ефекти більші, оскільки існує менше обмежень.
Коли заробітна плата зростає, фірма в короткостроковій перспективі застряє з його заданою кількістю K. У довгостроковій перспективі, однак, він зможе регулювати як L, так і K, і саме ця додаткова свобода руху гарантує принаймні таку ж велику або більшу реакцію при використанні вхідних даних та виході.
Для збільшення c принцип Ле Шательє відображається в тому, що попит на робочу силу набагато більш чуйний в довгостроковій перспективі, ніж у короткостроковій перспективі. У довгостроковій перспективі фірма може скористатися більшою перевагою шоку продуктивності праці, орендуючи більше машин та наймаючи ще більше робочої сили. Це, звичайно, відбивається на більшому прибутку, отриманому в довгостроковій перспективі у відповідь на збільшення c.
Цілісний погляд на фірму
Малюнки 14.1, 14.2 та 14.3 є фундаментальними графіками теорії фірми. Вони представляють три проблеми оптимізації, які, в унісон, складають теорію. Фірма - це не просто представлення вихідної сторони, але включає всі три проблеми оптимізації, як показано в робочій книзі Consistency.xls.
Мінімальна вхідна вартість (ізокванти та ізовитрати, які можуть бути використані для отримання функції витрат), максимальний вихідний прибуток (горизонтальний P з сімейством кривих витрат, які дають криву пропозиції) та графіки максимального прибутку на вході (горизонтальний w з MRP, що генерує криву попиту на вхід) всі переплітаються між собою. Всі вони не тільки дають послідовні відповіді на початкове рішення, але і всі вони забезпечують послідовні порівняльні статичні відповіді.
Якщо порівнювати короткострокові та довгострокові наслідки шоків, ми бачимо, що фірма реагує більш енергійно в довгостроковій перспективі. Еластичність заробітної плати праці більша (в абсолютному значенні) в довгостроковій перспективі і, завдяки послідовності, так і еластичність заробітної плати продукції. Аналогічно, c еластичності праці та випуску також більші в довгостроковій перспективі.
Обидва ці результати є прикладами принципу Ле Шательє: При меншій кількості обмежень швидкість реагування збільшується. Оскільки короткий пробіг запобігає зміні K, фірма менш здатна пристосовуватися до удару. Він може змінюватися лише L і, таким чином, його регулювання є більш обмеженим і нееластичним.
Вправи
-
Що відбувається в довгостроковій перспективі, коли ціна зростає на 1%? Реалізуйте шок і сфотографуйте результати, а потім вставте його в документ Word. Прокоментуйте зміни оптимальної робочої сили, капіталу, випуску продукції та прибутку.
-
Обчислити довгострокову еластичність вихідної ціни попиту на робочу силу. Покажіть свою роботу.
-
Застосовуйте те саме 1% підвищення ціни в короткостроковій перспективі. Сфотографуйте результати, а потім вставте їх у свій документ Word. Прокоментуйте зміни оптимальної робочої сили, капіталу, випуску продукції та прибутку.
-
Обчислити короткострокову вихідну ціну еластичності попиту на робочу силу. Покажіть свою роботу.
-
Порівняйте цінову еластичність попиту на робочу силу в довгостроковій (питання 2) і короткостроковій перспективі (питання 4). Чи працює тут принцип Ле Шательє? Поясніть, чому чи чому ні.
-
З вихідною ціною на 1% вище, збільште заробітну плату на 1% в довгостроковій та короткостроковій перспективі. Чи скасовують ці два потрясіння один одного в будь-якому випадку? Поясніть.
Посилання
Епіграф із сторінки 116 Євгена Зільберберга «Структура економіки: математичний аналіз» (1978). Це класична книга Math Econ, яка була популярним текстом на рівні випускників.
Майкл Сенберг, Арон Готтесман та Лалл Рамротанг, Пол Самуельсон «Будучи економіст» (2005), досліджують життя та внесок одного з найважливіших економістів 20-го століття.
