10: Виробнича функція
- Last updated
- Save as PDF
- Page ID
- 81917
Виробнича функція є основою теорії фірми. Він описує поточний стан технології та те, як вхід може бути перетворений у вихід.
Виробнича функція може відображатися різними способами, включаючи криві продукту та ізокванти. У кожну проблему оптимізації, з якою стикається фірма, включена виробнича функція.
Ключові визначення та припущення
Входи, також відомі як фактори виробництва, використовуються для виробництва продукції, яку іноді називають продуктом. Як показано на малюнку 10.1, фірма є дуже абстрактною сутністючорною коробкою, яка перетворює входи на вихід.
 Малюнок 10.1: Характер чорного ящика фірми.
Малюнок 10.1: Характер чорного ящика фірми.Конкретні деталі того, як організована фірма та як вона насправді поєднує входи для виготовлення товарів та послуг, ігноруються теорією, прихованою у чорній скриньці.
Вхідні матеріали часто поділяються на великі категорії, такі як земля, робоча сила, сировина та капітал. Спростимо ще далі, зруйнувавши все, що не є трудовою, в категорію капіталу.
Праця, Л, - це людська праця і зусилля. Вимірюється в одиницях часу, як правило, годинами.
Капітал має заплутану історію в економіці. Як фактор виробництва, капітал, K, означає речі, які виробляють інші речі, такі як машини, інструменти або обладнання. Це відрізняється від фінансового або венчурного капіталу, який є фондом грошей. Назва відомої книги Карла Маркса, Das Kapital, використовує капітал у сенсі багатства, номінований у грошах. Теорія K фірми вимірюється в числах машин.
Як і робоча сила, капітал орендується. Фірма не володіє жодними своїми машинами чи будівлями. Це вкрай нереально, але дозволяє уникнути складних питань, пов'язаних з амортизацією, фінансуванням закупівлі техніки (заборгованість проти власного капіталу, наприклад) тощо.
Ще одне крайнє спрощення припущення полягає в тому, що немає часу. Як і споживач максимізує корисність з урахуванням бюджетних обмежень, фірма існує лише для наносекунди. Він приймає рішення про те, скільки виробляти, щоб максимізувати прибуток, не турбуючись про запаси або траєкторію майбутніх продажів. Він видає вихід в одну мить.
Ми уникаємо ускладнень, що виникають при виробництві більше одного товару або послуги, припускаючи, що фірма виробляє тільки один продукт. Це робить доходи просто ціна рази кількість проданих одного продукту.
Не вдаючись знову в подробиці про нереалістичні припущення, здається корисним вказати, що ми не намагаємося побудувати точну модель реальної фірми. Наша основна мета полягає в тому, щоб вивести криву пропозиції. Ми хочемо знати, як фірма реагує на зміну ціни, незалежно від інших сторін. Припускаючи багато реальних ускладнень, ми можемо змоделювати проблему максимізації фірми, вирішити її та зробити порівняльну статику, щоб отримати криву пропозиції.
Математичне представлення
Так само, як і теорія поведінки споживачів, яка використовує корисну функцію для моделювання смаків та уподобань, Теорія фірми використовує виробничу функцію для захоплення здатності фірми перетворювати входи в виходи. На відміну від корисності, виробництво об'єктивне і спостережуване. Ми можемо порахувати, скільки виробляється вихід із заданої кількості годин праці та машин.
Виробничий набір описує всі технологічно здійснені виходи з заданої кількості входів. Виробнича функція описує максимально можливий вихід із заданої кількості вхідних даних. Зверніть увагу, як виробнича функція передбачає, що входи використовуються найкращим чином.
Найбільш абстрактним, загальним позначенням для виробничої функції є\(y = f(L, K)\). Він\(f()\) являє собою технологію, доступну фірмі. Конкретним, конкретним прикладом виробничої функції є функціональна форма Кобба-Дугласа:\(y=AL^\alpha K^\beta\). Давайте подивимося, як це виглядає в Excel.
КРОК Відкрийте книгу Excel ProductionFunction.xls, прочитайте аркуш Intro, потім перейдіть до технологічного аркуша, щоб побачити приклад виробничої функції.
На малюнку 10.2 виробничий набір - це поверхня 3D-об'єкта і все всередині; виробнича функція - це лише поверхня.
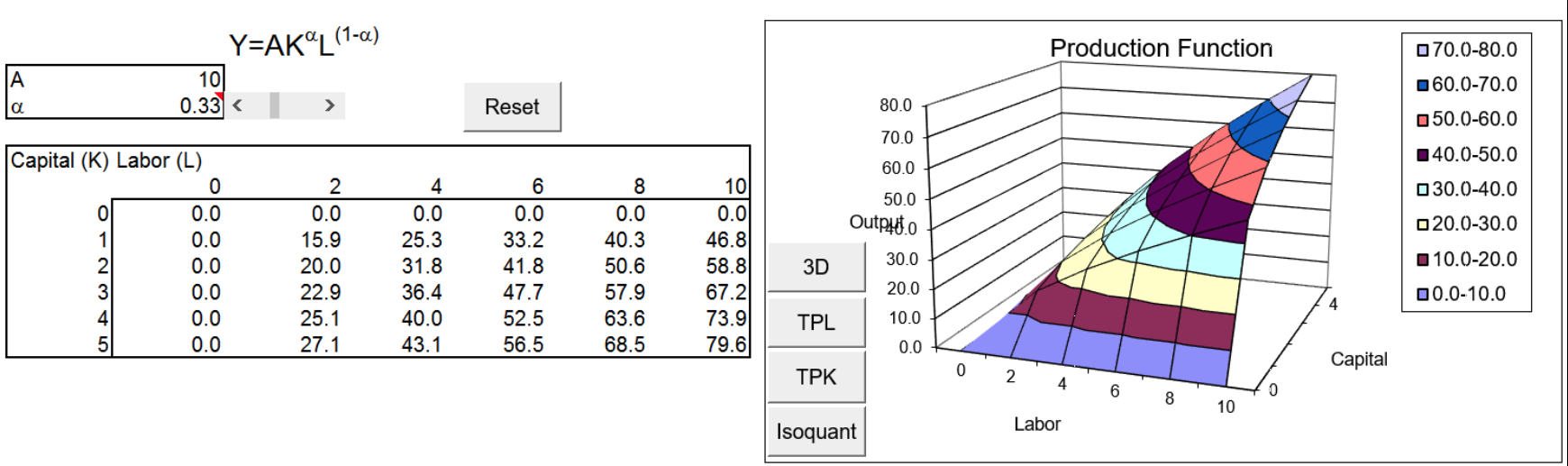
Малюнок 10.2: Виробнича функція.
Джерело: ProductionFunction.xls! Технологія.
Виробнича функція неявно включає в себе вже вирішену задачу інженерної оптимізації, вона дає максимальний вихід з будь-якої заданої комбінації входів. Іншими словами, ми припускаємо, що входи організовані в їх найбільш продуктивній конфігурації і нічого не витрачається даремно.
Зверніть увагу, що функція Кобба-Дугласа на технологічному аркуші була налаштована таким чином, щоб нею можна було керувати одним параметром\(\alpha\) (альфа), зробивши експоненти\(\alpha\) та (\(1 - \alpha\)). Використовуйте смугу прокрутки, щоб змінити альфа і помітити, як змінюється форма поверхні виробничої функції. Альфа - параметр, який приймає значення від нуля до одиниці.
КРОК Натисніть кнопку, щоб повернути аркуш в початкове положення за замовчуванням.
кнопку, щоб повернути аркуш в початкове положення за замовчуванням.
Криві продукту
Крім 3D виду, виробнича функція може відображатися і іншими способами. Щоб скласти графік виробничої функції в двох вимірах, нам потрібно придушити вісь. Якщо ми збережемо вихід і придушити одну з вхідних осей, ми отримаємо загальну криву добутку. Якщо ми пригнічуємо вихід і збережемо два входи, ми отримаємо isoquant.
Продукт і вихід означають одне і те ж. Загальна крива продукту - це кількість одиниць продукції, вироблених, оскільки один вхід змінюється, утримуючи іншу постійну.
КРОК Натисніть кнопки
кнопки і, щоб побачити криві продукту для праці та капіталу.
і, щоб побачити криві продукту для праці та капіталу.
Крім загальних кривих продукту, існують середні та граничні криві продукту. Середній продукт просто виводиться на одиницю введення. Таким чином, середній продукт праці - Y/L, а середній продукт капіталу - Y/K.
Граничні криві продукту говорять нам про додатковий вихід, який виробляється при збільшенні вхідного сигналу, утримуючи іншу вхідну постійну. Маржинальний продукт може бути обчислений на основі скінченних змін розміру на вході або через похідну.
За допомогою обчислення граничний продукт є просто похідною виробничої функції щодо вхідних даних. Для функції Кобба-Дугласа в технологічному аркуші граничні продукти знаходять шляхом взяття часткових похідних щодо L і K:\[MP_L = \frac{\partial Y}{\partial L}=(1 - \alpha)AK^\alpha L^{(1-\alpha)-1}=(1 - \alpha)AK^\alpha L^{-\alpha}\]\[MP_K = \frac{\partial Y}{\partial K}=\alpha AK^{\alpha -1}L^{1-\alpha}\]
КРОК Прокрутіть вниз і натисніть на комірку C52, щоб побачити, що граничний продукт обчислюється за допомогою зміни виходу від збільшення 2 годин праці, с\(K=4\).
Це обчислює граничний продукт праці як підйом над пробігом від\(L=0\) до\(L=2\) загальної кривої продукту.
КРОК Натисніть кнопку, а потім натисніть на комірку C58, щоб виявити граничний продукт, обчислений за допомогою похідної.
кнопку, а потім натисніть на комірку C58, щоб виявити граничний продукт, обчислений за допомогою похідної.
Оскільки загальний твір є кривою, то нахил дотичної лінії при не\(L=2\) такий, як підйом над прогоном з однієї точки в іншу.
КРОК Тепер подивіться на загальну, граничну та середню криві продукту.
Зверніть увагу, як криві продукту малюються на основі заданої суми капіталу. Якщо сума капіталу змінюється, то криві добутку зсуваються.
Маржинальний та середній продукт можна помістити разом, оскільки вони мають загальну шкалу осі y, вихід на одиницю вхідного сигналу. Загальна крива продукту ніколи не може бути позначена з граничними та середніми кривими продукту, оскільки загальна крива продукту використовує вихід як шкалу осі y.
Графіки демонструють, що при збільшенні загального продукту зі швидкістю зменшення маржинального продукту зменшується. Коли загальний вихід збільшується зі зменшенням швидкості, оскільки застосовується більше вхідних даних, у деяких випадках, ми підкоряємося закону зменшення віддачі. Поки альфа знаходиться між нулем і одиницею, наша виробнича функція Кобба-Дугласа демонструє зменшення віддачі.
Закон зменшення віддачі не заперечує, що можуть бути діапазони використання вхідних даних, де вихід збільшується зі зростаючою швидкістю. Це говорить, що, врешті-решт, подальше застосування більшої кількості вхідних даних разом з фіксованим коефіцієнтом виробництва повинно призвести до зменшення віддачі в тому сенсі, що випуск буде збільшуватися, але не так швидко, як раніше. Таким чином, Закон зменшення віддачі - це просто твердження про те, що гранична продуктивність, врешті-решт, повинна падати.
Як і у випадку з корисністю, функціональна форма Кобба-Дугласа зручна, але є багато-багато інших функціональних форм.
КРОК Перейдіть до поліноміального аркуша, щоб побачити іншу функціональну форму. Графіки разюче відрізняються, ніж раніше.
На відміну від функціональної форми Кобба-Дугласа, яка завжди показує зменшувальну віддачу, поліноміальна виробнича функція демонструє всі три різні фази віддачі: збільшення, зменшення та негативну віддачу.
При низьких рівнях використання робочої сили випуск збільшується зі зростаючою швидкістю, тому загальна крива продукту вигнута вгору, а граничний продукт збільшується. У цьому діапазоні, поки граничний продукт зростає, а випуск збільшується зі зростаючою швидкістю, випуск ракет вгору, зростає все швидше і швидше.
Коли гранична крива продукту досягає свого піку, загальна крива продукту знаходиться в точці перегину. Звідси додаткова праця призводить до збільшення обсягів виробництва, але зі зменшенням швидкості, вирівнюючись у міру збільшення L. Ми говоримо, що зменшуються віддачі встановили.
Поліноміальний аркуш має кольорове кодування, тому легко побачити, де загальна крива продукту змінює характер. Клітини з жовтим фоном сигналізують про діапазон використання праці, де застосовується зменшення віддачі.
Оскільки використовується все більше праці, загальний продукт досягає своєї максимальної точки (де граничний продукт дорівнює нулю). Крім цього, ми знаходимося в діапазоні негативних повернень. Це теоретична можливість, але не практична. Жодна фірма, що максимізує прибуток, ніколи не буде працювати в цьому регіоні, тому що ви можете отримати таку ж кількість продукції з меншою кількістю працівників.
Варто пам'ятати, що Закон про зменшення віддачі не говорить про те, що ми завжди маємо зменшувальну віддачу за кожен рівень використання праці. Замість цього закон говорить, що, врешті-решт, зменшиться віддача буде встановлена. Також важливо розуміти різницю між зменшенням і негативною віддачею. Перший каже, що випуск зростає, але повільніше і повільніше, тоді як останній каже, що вихід насправді падає.
Зверніть увагу на взаємозв'язок між граничною та середньою кривими продукту. Не випадково гранична крива добутку перетинає середню криву продукту при максимальному значенні середнього продукту. Існує гарантований зв'язок між граничними та середніми кривими: Всякий раз, коли граничний показник перевищує середнє, середнє має зростати, і всякий раз, коли граничний показник менше середнього, середній повинен падати. Таким чином, єдиний раз, коли дві криві зустрічаються, - це коли гранична і середня рівні.
КРОК Змініть параметр для коефіцієнта b з 30 на 40.
Зверніть увагу, що форма S стає набагато більш лінійною. Діапазон збільшення віддачі більший, і ми не потрапляємо в негативні віддачі над спостережуваним діапазоном L від 0 до 25.
КРОК Встановіть параметр для коефіцієнта b рівним 80.
За спостережуваним діапазоном L від 0 до 25 ми бачимо тільки зростаючі віддачі.
КРОК Змініть\(\delta L\) параметр з 1 на 2. Це змушує L піднятися на два, а діапазон йде від 0 до 50.
Зменшення віддачі роблять удар; це просто вимагає більше праці, щоб Закон зменшення повернення спостерігався, коли коефіцієнт b встановлений на 80.
Зменшення порівняно зі зменшенням віддачі
Одна надзвичайно заплутана річ про Закон зменшення повернення пов'язана з іншою концепцією, яка називається поверненням до масштабу. На відміну від закону зменшення повернень, Який заснований на застосуванні все більшої кількості певного входу, утримуючи інші входи константи, повертається до масштабу, фокусується на впливі на вихід зміни всіх входів однаковою пропорцією.
Немає закону для повернення до масштабу. Виробничий процес може демонструвати зростаючу, зменшувальну або постійну віддачу від масштабу для всіх значень використання вхідних даних. Наприклад, функція Кобба-Дугласа в технологічному аркуші має постійне повернення до масштабу, тому що якщо ви подвоїте L і K, ви гарантовано подвоїте вихід.
Ви можете переконатися в цьому, порівнявши пункти 2,2 і 4,4 в таблиці в Технологічному аркуші. Більш повна демонстрація використовує трохи алгебри.
Почнемо з виробничої функції:\[AK^\alpha L^{1-\alpha}\] Далі ми подвоюємо як L, так і K:\[A(2K)^\alpha (2L)^{1-\alpha}\] Ми розширюємо терміни з показниками:\[A(2^\alpha) (K^\alpha) (2^{1-\alpha})(L^{1-\alpha})\] Ми збираємо терміни «2":\[A(2^{\alpha + (1-\alpha)} (K^\alpha) (L^{1-\alpha})\] Альфи додають до нуля (\(\alpha - alpha = 0\)), тому ми отримуємо:\[A2K^\alpha L^{1-\alpha}\] Таким чином, ми показали, що подвоєння входи з будь-яких вхідних рівнів призводить до подвоєння виходу, і це називається постійним поверненням до масштабу. Якщо експоненти у функції Кобба-Дугласа не сумуються 1, то функція не проявляє цю властивість.
Функція Кобба-Дугласа в технологічному аркуші підпорядковується Закону зменшення віддачі для кожного входу (з\(0 < \alpha <1\)), але вона має постійну віддачу до масштабу. Чи означає зменшення віддачі зменшення віддачі від масштабу? Ні, абсолютно ні. Ці два поняття є незалежними. Вони задають різні питання. Закон зменшення повернення - це про те, що відбувається з виходом, коли один вхід збільшується, без обмежень, і зменшення повернення до масштабу говорить, що вихід буде менше, ніж удвічі, коли всі входи подвоюються.
Ізокванти
На додаток до кривих продукту, ще один спосіб представлення виробничої функції використовує ізоквант. Префікс iso, що означає рівний або однаковий (як у рівнобедреному трикутнику), поєднується з квантом (посилаючись на кількість виводу), щоб передати ідею, що ізоквант відображає комбінації L і K, які дають однаковий вихід.
КРОК Поверніться у верхню частину технологічного аркуша та натисніть кнопку (біля комірки H28), щоб побачити карту isoquant, як показано на малюнку 10.3.
кнопку (біля комірки H28), щоб побачити карту isoquant, як показано на малюнку 10.3.
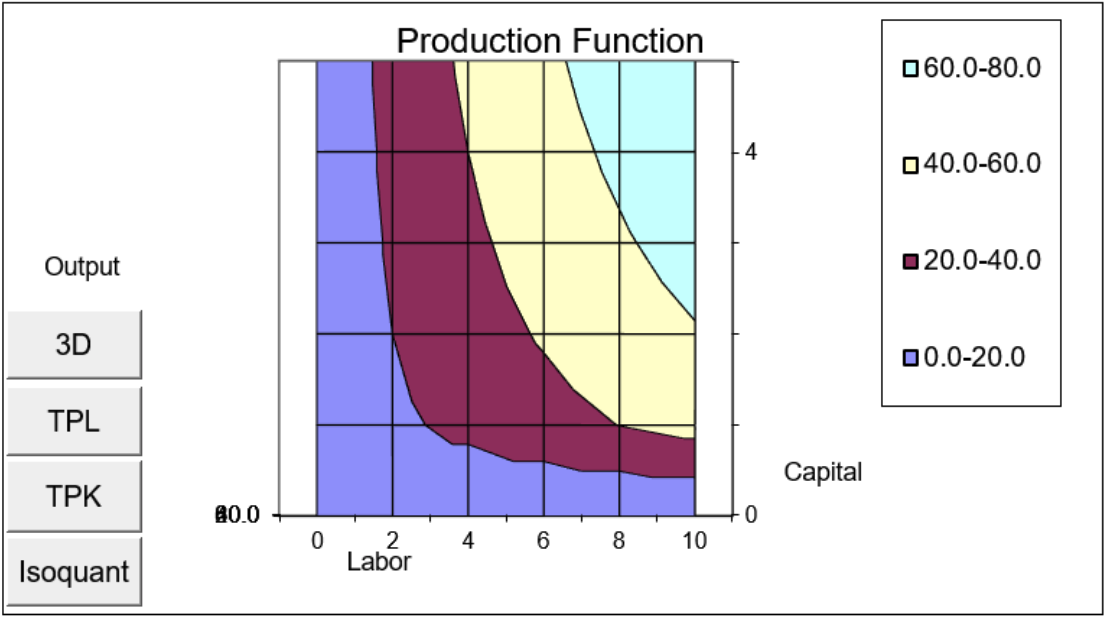
Малюнок 10.3: Ізокванти для технології Кобба-Дугласа.
Джерело: ProductionFunction.xls! Технологія.
Ізоквант - це просто 2D, вид зверху вниз 3D поверхні. На відміну від кривих добутку, які дають вид збоку, ізоквант показує L і K на осях x і y відповідно і пригнічує вихід.
Зверніть увагу, що Excel не може правильно намалювати карту isoquant, поклавши спотворені символи в нижньому лівому куті діаграми та створюючи химерний, зубчастий дисплей внизу.
Можливо, ви думаєте, що це дуже схоже на карту байдужості. Існують, безумовно, сильні паралелі між ізоквантами та кривими байдужості. Обидва є переглядами 3D-об'єкта зверху вниз і, отже, обидва є кривими рівня або контурними графіками. Обидва використовуються для пошуку та відображення рішення проблеми оптимізації.
Однак є одна критична відмінність: на відміну від кривої байдужості, кожен ізоквант, в принципі, безпосередньо спостерігається і ізокванти можна порівняти за кардинальною шкалою. З кривими байдужості функція корисності є зручною вигадкою, а числові значення лише відображають рейтинги. Нікого не хвилює, що певна крива байдужості дає 28 утиліт задоволення. Це не стосується ізоквантів, оскільки пригнічена вісь, вихід, вимірюється. Можна, звичайно, сказати, що один ізоквант дає вдвічі більший вихід, ніж інший, або що один ізоквант дає на 17 більше одиниць виходу, ніж інший.
Один із способів, у якому криві байдужості та ізокванти однакові, полягає в тому, що ми можемо обчислити нахил між двома точками або миттєву швидкість зміни в точці на ізокванті. Щоб уникнути плутанини з MRS, ми називаємо цей нахил технічною нормою заміщення, TRS. З робочою силою на осі x та капіталом на осі y TRS говорить нам, скільки капіталу ми можемо заощадити, якщо для отримання того ж рівня випуску буде використана ще одна одиниця праці.
З однієї точки в іншу TRS можна обчислити як підйом над пробігом,\(\frac{\delta K}{\delta L}\). У точці ми обчислюємо TRS як відношення похідних по відношенню до L і K від виробничої функції:\[TRS=-\frac{MP_L}{MP_K}=-\frac{\frac{\partial f(L,K)}{\partial L}}{\frac{\partial f(L,K)}{\partial K}}\] Тоді як MRS універсально використовується для нахилу кривої байдужості, MRTS (гранична швидкість технічного заміщення) іноді використовується для нахилу ізоквантний. MRTS і TRS - ідеальні синоніми. Ми будемо використовувати TRS.
TRS (як MRS) - це число, яке виражає замінність праці для капіталу в точці на ізокванті. Отже, TRS двох різних комбінацій L і K на одному ізокванті може бути\(-100\) і\(-2\). \(-100\)Значення TRS = говорить про те, що фірма може замінити 100 одиниць капіталу на 1 одиницю праці і все одно виробляти таку ж продукцію. Ізоквант був би крутим у цій точці. Якщо точка має TRS =\(-2\), 1 одиниця праці може замінити 2 одиниці капіталу, щоб отримати той же вихід. Ізоквант у цій точці був би набагато рівнішим, ніж точка з TRS =\(- 100\).
Так само, як MRS, TRS говорить нам, наскільки крутий isoquant знаходиться в точці. Чим крутіше ізоквант, тим більше капіталу можна замінити робочою силою і все одно виробляти ту саму продукцію.
Технологічний прогрес
З плином часу технологія покращується ваша здатність перетворювати входи на вихід. Електроенергія та комп'ютери є прикладами технічного прогресу, який дозволяє виробляти більше вихідних даних з одного і того ж входу.
Існує два види технологічних змін. Функціональна форма Кобба-Дугласа може бути використана для ілюстрації кожного типу.
Припустимо, підвищена освіта покращує продуктивність праці. Це було б змодельовано як збільшення показника праці у виробничій функції Кобба-Дугласа. Невеликі зміни, скажімо, від 0,75 до 0,751, призводять до великих відповідей (наприклад, у виробництві або використанні робочої сили), оскільки ми працюємо з показником. Це відоме як технологічні зміни, що підсилюють працю.
У нас також може виникнути ситуація, коли коефіцієнт А у функції\(AK^\alpha L^\beta\) збільшувався з часом. Коли A піднімається, така ж кількість входів може зробити більше виходу. Цей технологічний прогрес вважається нейтральним (з точки зору використання L і K), оскільки TRS не залежить від А.
Ми можемо показати це, пройшовши кроки, необхідні для пошуку TRS. Спочатку обчислюємо граничні добутки L і K з функції,\(Y=AL^\alpha K^\beta\):\[MP_L = \frac{\partial Y}{\partial L}= \alpha A L^{\alpha-1}K^\beta\]\[MP_K = \frac{\partial Y}{\partial K}=\beta AL^\alpha K^{\beta -1}\] TRS мінус відношення граничних продуктів:\[TRS=-\frac{MP_L}{MP_K}=-\frac{\alpha A L^{\alpha-1}K^\beta}{\beta AL^\alpha K^{\beta -1}}=-\frac{\alpha K}{\beta L}\] Терміни A скасовують, що означає, що співвідношення граничної продуктивності кожен вхід залежить лише від показника кожного входу та кількості використовуваного вхідного сигналу.
Фірма як виробнича функція
Виробнича функція є відправною точкою для теорії фірми. Як і у випадку з корисністю, багато, багато функціональних форм можуть бути використані для представлення реальних виробничих процесів.
Економісти представляють виробничу функцію не як 3D-об'єкт, а в двох вимірах. Ми отримуємо криві добутку (загальна, гранична та середня криві продукту), фокусуючись на виході як функції одного входу, утримуючи всі інші входи постійними. Ізоквант пригнічує вихід і показує різні комбінації L і K, які виробляють заданий рівень виходу.
TRS схожий на MRS, і він відіграватиме важливу роль у розумінні вибору вхідних даних мінімізації витрат фірми.
Не забудьте зберегти прямо різницю між Законом зменшення віддачі та ідеєю повернення до масштабу. Перший застосовує все більше і більше одного входу, утримуючи всі інші входи постійними; останній повідомляє, що відбувається з виходом, коли всі входи змінюються однаковою пропорцією. Це дві різні речі.
Вправи
-
Починаючи з порожньої книги, з K = 100, намалюйте загальну, граничну та середню криві добутку для L = 1 до 100 на 1 для виробничої функції Кобба-Дугласа\(Q=L^\alpha K^\beta\), де\(\alpha = 3/4\) і\(\beta = 1/2\). Використовуйте похідну для обчислення граничного продукту праці.
Підказка: Позначте комірки в рядку у стовпцях A, B, C та D як L, Q, MPL та APL. Для L створіть список чисел від 1 до 100. Для інших трьох стовпців введіть відповідну формулу і заповніть. Для MPL не використовуйте зміну Q, розділену на зміну L; замість цього введіть формулу для похідної для MPL у точці.
-
Для якого діапазону L функція Кобба-Дугласа в питанні 1 демонструє закон зменшення віддачі? Помістіть свою відповідь у текстове поле у вашій робочій книзі.
-
Визначте, чи має ця функція збільшення, зменшення або постійне повернення до масштабу. Використовуйте робочу книгу для обчислень і включіть свою відповідь у текстове поле.
-
З вашої роботи в питанні 3 та коментаря в тексті, що ви не можете мати постійних повернень до масштабу «якщо показники у функції Кобба-Дугласа не підсумовуються до 1», надайте правило для визначення повернення до масштабу для функціональної форми Кобба-Дугласа.
-
Чи можливо виробнича функція одночасно демонструвати Закон зменшення віддачі та збільшення віддачі від масштабу? Якщо так, наведемо приклад. Помістіть свою відповідь у текстове поле у вашій робочій книзі.
-
Намалюйте ізоквант для 50 одиниць виводу для функції Кобба-Дугласа в питанні 1.
Підказка: Використовуйте алгебру, щоб знайти рівняння, яке повідомляє вам K, необхідний для отримання 50 одиниць, заданих L. Створіть стовпець для K, який використовує це рівняння на основі L в діапазоні від 20 до 40 на 1, а потім створіть діаграму даних L і K.
-
Обчислити ТРС функції Кобба-Дугласа при L = 23, K = 312,5. Покажіть свою роботу в електронній таблиці.
Посилання
Епіграф походить зі сторінки 152 «Теорія виробництва» Чарльза В. Кобба та Пола Дугласа, Американський економічний огляд, Том 18, № 1, Додаток, Документи та матеріали сорокової щорічної зустрічі Американської економічної асоціації (березень, 1928), стор. 139—165, www.jstor.org/стайна/1811556.
Дуглас, досвідчений професор і сенатор США від штату Іллінойс, пояснив, як вони з Коббом використовували функціональну форму, яка буде названа на їх честь:
Потім я тимчасово читав лекції в Амхерстському коледжі і консультувався зі своїм другом і колегою Чарльзом Коббом, математиком. За пропозицією останнього\(P = bL_kC_{k-1}\) була прийнята формула, форма, яку також використовували Вікстід та Вікселл.
Див. С. 904 у Paul H. Дуглас, «Виробнича функція Кобба-Дугласа ще раз: її історія, її випробування та деякі нові емпіричні цінності», Журнал політичної економії, Vol. 84, № 5 (жовтень 1976), pp. 903—916, www.jstor.org/stable/1830435
