2.2: Функції утиліти

Раніше ми показали, що у споживача є переваги, які можна розкрити та нанести на карту. Наступним кроком є виявлення тієї чи іншої функціональної форми, званої корисною функцією, яка вірно представляє переваги людини. Як тільки ви зрозумієте, як працює функція утиліти, ми можемо поєднати її з обмеженням бюджету, щоб вирішити проблему оптимізації споживача.

Кардинал і порядкові рейтинги

Джеремі Бентам (1748-1832) був утилітарним філософом, який вважав, що теоретично можна виміряти кількість корисності від споживання певної кількості товару. Так, наприклад, коли ви з'їли яблуко, ми могли б підключити вас до якогось пристрою, який повідомить про кількість отриманих «утиліт» задоволення. Слово utils знаходиться в лапках, тому що вони насправді не існують, але Бентам вважав, що вони це зробили, і одного дня буде виявлено за допомогою передового вимірювального приладу. Ця остання частина не настільки божевільна машина fMRI - це саме те, що він передбачав.

Бентам також вважав, що утиліти - це свого роду загальна валюта, яка дозволила їм порівнювати між окремими особами. Він вважав, що суспільство повинно максимізувати сукупність або загальну корисність, а утилітаризм став асоціюватися з фразою «найбільше щастя для найбільшої кількості». Таким чином, якщо я отримую 12 utils від споживання яблука, а ви отримаєте 6, то я повинен отримати яблуко. Утилітаризм також має на увазі, що якщо я отримаю більше утиліт від удару вас в обличчя, ніж ви втратите, я повинен пробити вас. Ось чому утилітаризм сьогодні не високо цінується.

Цей погляд на корисність розглядає задоволення так, ніби ми могли розмістити його в кардинальному масштабі. Це звичайна числова лінія, де 8 вдвічі більше, ніж 4, а різниця між 33 і 30 така ж, як і між 210 і 207.

Близько рубежу ^20-го століття Вільфредо Парето (1848-1923, вимовляється Pa-ray-toe) створив сучасний спосіб мислення про корисність. Він вважав, що задоволення не може бути поставлено в кардинальних масштабах і що ви ніколи не можете порівняти комунальні послуги двох людей. Замість цього він стверджував, що корисність може вимірюватися тільки до порядкової шкали, в якій є все вище і нижче, але ніяк не можна виміряти величину між двома пунктами.

Зверніть увагу, як підхід Парето відповідає саме тому, як ми припускали, що споживач може вибирати між пачками товарів як віддає перевагу одному пакету або байдужий. Ми ніколи не стверджували, що можемо виміряти певну кількість задоволеності від певного пакету.

Для Парето та сучасної економіки числове значення від певної корисної функції для даної комбінації товарів не має сенсу. Ці значення схожі на систему рейтингу зірок для ресторанів.

Припустимо, Critic A використовує 10-бальну шкалу, тоді як Critic B використовує 1000-бальну шкалу, щоб судити про ті ж ресторани. Ми ніколи не сказали б, що найгірший ресторан B, який забив, скажімо, 114, кращий, ніж кращий A, ідеальний 10. Замість цього ми порівнюємо їх рейтинги. Якщо A і B дають одному ресторану найвищий рейтинг (незалежно від балу), це найкращий ресторан.

Тепер припустимо, ми читаємо журнал, який використовує 5-зіркову рейтингову систему. Ресторан X заробляє 4 зірки, а ресторан Y 2 зірки. X краще, але чи можемо ми зробити висновок, що X вдвічі краще, ніж Y? Абсолютно ні. Порядкова шкала впорядкована, але відмінності між значеннями не важливі.

Парето революціонізував наше розуміння корисності. Він відкинув кардинальну шкалу Бентама, оскільки не вірив, що задоволення можна виміряти як температуру тіла або артеріальний тиск. Парето показав, що ми можемо вивести криві попиту з менш обмежувальним більш-менш ранжируванням пучків.

Перехід від кардинального погляду Бентама на корисність до порядкового погляду Парето був непростим. Використання того ж слова, корисність, створює плутанину (хоча, чесно кажучи, Парето намагався створити нове слово, офелімічність, але воно так і не зачепилося). Слід повторювати, що для сучасного економіста, хоча корисна функція покаже числові значення, їх не слід інтерпретувати в кардинальній шкалі, а також не слід порівнювати числові утиліти різних людей. Оскільки ми не можемо проводити міжособистісні порівняння корисності для додавання утиліт різних людей, ми не можемо дати мені яблуко або дозволити мені пробити вас.

Монотонне перетворення

Як тільки ми розкриємо криву байдужості споживача та карту, ми отримаємо рейтинг споживачів усіх можливих пакетів. Тоді все, що нам потрібно зробити, це використовувати функцію, яка вірно представляє криві байдужості. Функція утиліти - це зручний спосіб захоплення замовлення споживача.

Існує безліч (по суті, нескінченність) функцій, які могли б працювати. Все, що потрібно зробити, - це зберегти рейтинг переваг споживача.

Монотонне перетворення - це правило, застосоване до функції, яка змінює (перетворює) її, але підтримує початковий порядок виходів функції для заданих входів. Монотонний - це технічний термін, який означає завжди рухатися в одному напрямку.

Наприклад, рейтинги зірок можуть бути зведені в квадрат, а рейтинги залишаються незмінними. Якщо X - це 4-зірковий ресторан, а Y - 2-зірковий ресторан, ми можемо їх квадратувати. X тепер має 16 зірок, а Y має 4 зірки. X все ще вище, ніж Y. У цьому випадку квадратування є монотонним перетворенням, оскільки воно зберегло впорядкування, а X все ще вище, ніж Y.

Чи можемо ми зробити висновок, що X тепер в чотири рази краще? Звичайно, ні. Пам'ятайте, що рейтинг зірок є порядковою шкалою, тому відстань між елементами не має значення. Ми говоримо, що квадрат - це монотонне перетворення, оскільки воно підтримує однаковий порядок, і ми не дбаємо про відстані між числовими значеннями. Єдине їх значення - «вище» і «нижче», які вказують на краще і гірше.

Фактом є те, що MRS (в будь-який момент) залишається постійною при будь-якому монотонному перетворенні. Це важлива властивість монотонних перетворень, яке ми проілюструємо на конкретному прикладі в Excel.

Кобба-Дуглас: всюдисуща функціональна форма

КРОК Відкрийте книгу Excel Utility.xls, прочитайте лист Intro, а потім перейдіть на лист CobbDouglas, щоб побачити приклад цієї утиліти функції:\[u(x_1, x_2) = x_1^cx_2^d\]

В економіці функція, створена шляхом множення змінних, які підносяться до повноважень, називається функціональною формою Кобба-Дугласа.

КРОК Дотримуйтесь вказівок на аркуші (у стовпці K), щоб повернути 2D-діаграму, щоб ви дивилися на неї вниз.

Вид функції утиліти зверху вниз виглядає як карта байдужості. Сама функція утиліти, в 3D, - це пагорб або гора (яка продовжує рости, не досягаючи ніколи не досягаючи топілюстрації ідеї ненаситності).

За допомогою корисної функції криві байдужості відображаються як контурні лінії або криві рівня. Криві в 2D просторі створюються шляхом взяття горизонтальних зрізів 3D-поверхні. Кожна точка на кривій байдужості має точно таку ж висоту, що є корисністю.

КРОК Показники (c і d) в функції утиліти виражають «любить і не любить». Спробуйте c = 4, потім c = 0,2 в осередку B5.

Чим вище показник c, тим більше подобається споживачеві,\(x_1\) оскільки кожна одиниця\(x_1\) підвищується до більшої потужності, оскільки c збільшується. Зверніть увагу, що при c = 4, той факт, що споживачеві подобається\(x_1\) набагато більше, ніж коли c = 0,2 відбивається на формі кривої байдужості. Чим крутіше крива байдужості, тим вище MRS (в абсолютному значенні) і тим більше подобається споживачеві\(x_1\).

КРОК. Приступаємо до листа CobbDouglasLN, на якому застосовується монотонне перетворення функції Кобба-Дугласа. Він застосовує функцію природного журналу до функції утиліти.

Нагадаємо, що натуральний логарифм числа x є показником на e (ірраціональне число 2.7128.), що робить результат рівним x. Також слід пам'ятати, що існують особливі правила роботи з колодами. Два особливо поширених правила -\(\ln (x^y) = y \ln x\) і\(\ln (xy) = \ln x + \ln y\). Ми можемо застосувати ці правила до функції Кобба-Дугласа, коли беремо природний журнал:

\(u(x_1, x_2) = x_1^cx_2^d\)

\(\ln [u(x_1, x_2)] = \ln [x_1^cx_2^d]\)

\(\ln [u(x_1, x_2)] = c \ln x_1 + d \ln x_2\)

Лист CobbDouglasLN застосовує природне перетворення журналу за допомогою функції LN () Excel.

КРОК Натисніть на будь-яку комірку між B12 та Q27, щоб побачити формулу. Ми обчислюємо природний журнал корисності, який\(x_1\) піднімається до часу потужності c,\(x_2\) піднятого до потужності d.

Як оригінальна функція утиліти порівнюється з її природною версією журналу?

КРОК Перейти вперед і назад кілька разів між ними (натисніть на CobbDouglas лист вкладку, а потім на CobbDouglassLN лист вкладка). Очевидно, що цифри різні.

Але ви помітили щось цікаве?

КРОК Порівняйте комірки з жовтим фоном на двох аркушах, щоб побачити, що ці дві комбінації продовжують лежати на одній кривій байдужості, хоча значення корисності двох функцій різні.

Той факт, що клітини залишаються на тій же кривій байдужості після проходження природного перетворення колоди, демонструє значення монотонного перетворення. Значення корисності різні, але рейтинг збережений. Обидві функції утиліти підтримують однаковий зв'язок між 1,14 та 2,7 та кожним іншим зв'язком.

Отже, тепер ви знаєте, що функція корисності Кобба-Дугласа може бути використана для вірного представлення переваг споживача (включаючи налаштування показників c і d, щоб зробити криві крутішими або лесткішими), і що ми можемо використовувати природне перетворення журналу, якщо хочемо. Крім того, економісти часто використовують функціональну форму Кобба-Дугласа для корисних (і виробничих) функцій, оскільки вона має дуже приємні алгебраїчні властивості, де багато термінів скасовуються.

Функція Кобба-Дугласа особливо проста в роботі, якщо пам'ятати наступні правила:

Правила алгебри:\(\frac{x^a}{x^b} = x^{a - b}\) і\(x^{a^b} = x^{ab}\)

Правило обчислення:\(\frac{dax^b}{dx} = bax^{b - 1}dx\)

Ці правила зараз можуть здатися неактуальними, але ми побачимо, що вони значно полегшують роботу з функцією Кобба-Дугласа, ніж з іншими функціями. Це багато в поясненні неодноразового використання функціональної форми Кобба-Дугласа в економіці.

Висловлення інших параметрів за допомогою службових функцій

КРОК. Приступайте до листа PerfSub і озирніться навколо. Прокрутіть вниз (якщо потрібно) і подивіться на дві діаграми.

Зверніть увагу, як ця функціональна форма створює прямі криві байдужості (на 2D діаграмі). Якби споживач розглядав два товари як ідеальні замінники, ми б використовували цю функціональну форму замість Кобба-Дугласа. Коефіцієнти (a і b) можна налаштувати, щоб зробити лінії крутішими або плоскими.

КРОК. Приступаємо до листа PerfComp. Це показує, як функціональна форма min () створює Г-подібні криві байдужості.

Функція min () виводить менший з двох членів,\(ax_1\) і\(bx_2\). Це означає, що отримання більше одного блага, утримуючи кількість іншої хорошої константи, не збільшує корисність. При цьому утворюється Г-подібна крива байдужості.

Нарешті, квазілінійний аркуш відображає криві байдужості, які насправді вигнуті, але досить плоскі.

КРОК Перейдіть до квазілінійного аркуша і натисніть на різні варіанти функціональної форми. Це лише деякі з багатьох перетворень, які можуть бути застосовані до,\(x_1\) а потім додані для\(x_2\) отримання того, що називається квазілінійною корисністю. Пізніше ми побачимо, що ця функціональна форма має інші властивості, ніж Кобб-Дуглас.

Зауважте, що ми можемо представляти багато різних видів переваг за допомогою службових функцій. Важливим моментом є те, що існує безліч (а точніше, нескінченність) можливих функцій корисності, доступних нам. Ми б вибрали той, який вірно відображає переваги конкретного споживача. Ми завжди можемо застосувати монотонну трансформацію, і це не змінить уподобань споживача.

Обчислення MRS для корисної функції

Тепер, коли у нас є службові функції для представлення переваг споживача, ми можемо обчислити MRS з однієї точки в іншу (як ми це робили в попередньому розділі) або за допомогою миттєвої швидкості зміни, більш відомої як похідна.

Це не книга з математики, але економісти використовують математику, тому нам потрібно точно бачити, як працює похідна. Основна ідея - конвергенція: зробіть зміну x (пробігу) все менше і менше, і співвідношення підйому над пробігом (нахилом) стає все ближче і ближче до його кінцевого значення. Похідна - це ярлик, який дає нам відповідь без громіздкого процесу внесення змін до менших і менших.

Але це занадто абстрактно. Ми можемо побачити це в Excel.

КРОК Перейдіть до аркуша MRS, щоб побачити, як MRS можна обчислити за допомогою дискретної зміни розміру порівняно з нескінченно невеликою зміною.

Функція утиліти є\(x_1x_2\). Це Кобба-Дугласа з показниками (неявно), рівними 1.

Припустимо, нас цікавить крива байдужості, яка дає всі комбінації з корисністю 10. Звичайно 5,2 працює (з 5 разів 2 це 10). Вона являє собою червону крапку на графіку на аркуші MRS (і на рис. 2.10).

Малюнок 10: Обчислення MRS.

Джерело: Utility.xls! ПАНІ

З пачки 5,2, якби ми дали цьому споживачеві ще 1 одиницю\(x_1\), на скільки нам довелося б зменшити,\(x_2\) щоб залишитися на кривій\(U=10\) байдужості? Трохи алгебри розповідає нам.

Ми знаємо, що\(U = x_1x_2\) і початкова зв'язка 5,2 дає\(U = 10\). Ми хочемо підтримувати U константу з,\(x_1 = 6\) тому що ми додали одну одиницю\(x_1\), тому ми маємо:

\(U = x_1x_2\)

\(10 = 6x_2\)

\(x_2 = \frac{10}{6}\)

У нас є два пучка, які дають\(U = 10\) (5,2, і 6,\(\frac{10}{6}\)). Ми можемо обчислити MRS як зміна в\(x_2\) розділеному на зміну в\(x_1\). Дельта (або різниця) в\(x_2\) є\(-\frac{1}{3}\) (тому що\(\frac{10}{6}\)\(\frac{1}{3}\) менше 2), а дельта в\(x_1\) 1 (6 - 5), тому починаючи з точки 5,2, MRS від\(x_1\) = 5 до \(x_1\)= 6 є\(-\frac{1}{3}\). Це те, що Excel показує в комірці C18.

Інший спосіб обчислення MRS використовує підхід обчислення. Замість «великого» або дискретного зміни розміру приймаємо нескінченно малу зміну, обчислюючи нахил кривої байдужості не від однієї точки до іншої, а як нахил дотичної лінії (як показано на малюнку 2.10).\(x_1\) Ми використовуємо похідну для обчислення MRS в певній точці.

Для цієї простої утиліти функції, утримуючи U константу на 10, ми можемо переписати функцію як\(x_2\) в терміні\(x_1\), потім взяти похідну.

\(U = x_1x_2\)

\(x_2 = \frac{10}{x_1}\)

\(\frac{dx_2}{dx_1} = - \frac{10}{x_1^2}\)

В\(x_1 = 5\), підставляємо в цьому значенні і MRS в цій точці\(-\frac{10}{25}\) або -0,4. Це те, що Excel показує в комірці D18. Якщо вам потрібна допомога з похідними, в наступному розділі є додаток, в якому розглядаються основні обчислення.

Обчислення MRS таким чином спирається на здатність писати з\(x_2\) точки зору\(x_1\). Якщо у нас є службова функція, яку неможливо легко переставити таким чином, ми не зможемо обчислити MRS. Однак існує більш загальний підхід. Процедура передбачає взяття похідної від корисної функції щодо\(x_1\) (називається граничною корисністю\(x_1\)) і ділення на похідну від корисної функції щодо\(x_2\) (називається граничною корисністю \(x_2\)). Не забудьте включити знак мінус при використанні такого підходу. Ось як це працює.

З\(U = x_1x_2\), похідні прості:\(\frac{dU}{dx_1} = x_2\) і\(\frac{dU}{dx_2} = x_1\). Таким чином, ми можемо підставити їх в чисельник і знаменник виразу MRS:

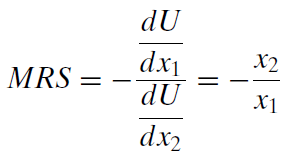
Оскільки ми розглядаємо пункт 5,2, ми оцінюємо MRS в цей момент (що означає, що ми підключаємо ці значення до нашого вираження MRS), як це:

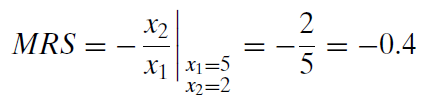
Відзначимо, що мінус співвідношення граничних комунальних послуг дає ту ж відповідь, що і\(\frac{dx_2}{dx_1}\) метод. Обидва використовують нескінченно малі зміни для обчислення миттєвої швидкості зміни кривої байдужості в певній точці.

Також зауважте, що співвідношення граничного підходу комунальних послуг вимагає, щоб ви розділили граничну корисність\(x_1\) (благо на осі x) на граничну корисність\(x_2\) (благо на осі y). Оскільки ми використовували\(\frac{\Delta y}{\Delta x}\) підхід до зміни дискретного розміру, легко переплутати чисельник і знаменник при обчисленні MRS через похідну. Пам'ятайте, що\(\frac{dU}{dx_1}\) йде в чисельнику.

Порівняння\(\Delta\) і d методи

Поки що ми знаємо, що існує два способи отримати MRS: рухатися з однієї точки в іншу вздовж кривої байдужості (дискретна зміна\(\Delta\)) або нахил дотичної лінії в точці (нескінченно мала зміна, г). Ми також знаємо, що у нас є два способи зробити останнє (вирішити для\(x_2\) цього взяти похідну або обчислити співвідношення граничних комунальних послуг.)

Але ви, можливо, помітили потенційну проблему в тому, що дві процедури для отримання MRS дають різні відповіді. У аркуші MRS та нашій роботі вище, дискретний підхід до змін говорить нам, що MRS, як вимірюється від\(x_1 = 5\) до\(x_1 = 6\) є\(-\frac{1}{3}\), тоді як похідний метод говорить, що MRS при\(x_1 = 5\) -0,4.

Ця різниця в виміряних MRS обумовлена тим, що два підходи застосовують\(x_1\) різну зміну розміру кривої. Оскільки зміна дискретного розміру стає меншою, вона наближається до похідної міри MRS. Ви можете це чітко бачити за допомогою Excel.

КРОК Змініть розмір кроку в комірці B7 на 0.5 і спостерігайте, як змінюється клітина C18. Зверніть увагу, що діаграма також трохи відрізняється, тому що точка в\(x_1 = 6\) даний час на 5.5.

Ви зробили розмір зміни\(x_1\) меншим, так що точка тепер ближче до початкового значення, 5.

КРОК Зробіть це ще раз, на цей раз змінивши розмір кроку в осередку B7 на 0.1. Точка з\(x_1 = 5.1\) настільки близька до 5, що її важко побачити, але вона є. Зробіть одну останню зміну розміру кроку, встановивши його на 0,01.

З розміром кроку 0,01, ви не можете побачити початкову та нову точки, оскільки вони так близько один до одного, але вони все ще є дискретною відстанню один від одного. Excel відображає точка-точка дельта-обчислення в комірці C18. Це дійсно близько до похідної міри MRS в осередку D18, оскільки похідна є просто кульмінацією цього процесу внесення змін до\(x_1\) менших і менших.

На малюнку 2.10 підхід до дискретних змін обчислює підйом над прогоном за допомогою двох окремих точок на кривій, тоді як підхід обчислення обчислює нахил дотичної лінії.

КРОК Подивіться на значення осередків в жовтому виділеному рядку.

MRS для даного підходу точно такі ж. Іншими словами, стовпці C, H і M однакові, а стовпці D, I і N однакові. Це показує, що MRS залишається незмінним, коли функція утиліти монотонно трансформується.

Функції утиліти представляють переваги

Функції корисності - це рівняння, які представляють переваги споживача. Ідея полягає в тому, що ми розкриваємо переваги, змусивши споживача порівняти зв'язки, а потім підбираємо функціональну форму, яка вірно відображає криві байдужості споживача.

У підборі функціональної форми існує безліч можливостей і економісти часто використовують форму Кобба-Дугласа. Значення корисності, вироблені шляхом введення кількості товарів, безглузді, і будь-яке монотонне перетворення (оскільки воно зберігає упорядкування переваг) буде працювати як корисна функція. Монотонні перетворення не впливають на MRS.

MRS є важливим поняттям в теорії споживачів. Це говорить нам про готовність торгувати одне благо на інше, і цей показник любить і не любить споживача. Готовність торгувати багато у за трохи х дає високу MRS (в абсолютному значенні), і це говорить про те, що споживчі значення x більше, ніж у.

MRS обчислюється з однієї точки в іншу (\(\Delta\)), але її також можна обчислити за допомогою похідної (d) в точці. Обидва дійсні і отримане число для MRS інтерпретується однаково (готовність торгувати).

вправи

Функція\(U = x - 0.03x^2 + y\) корисності має квазілінійну функціональну форму. Скористайтеся цією функцією, щоб відповісти на запитання нижче. Ви можете побачити, як це виглядає, вибравши опцію Polynomial на Квазілінійному аркуші.

1. Обчислити значення корисної функції в зв'язці A, де x = 10 і y = 1. Покажіть свою роботу.
2. Працюючи з зв'язкою А, знайдіть MRS, коли х піднімається від x = 10 до x = 20. Покажіть свою роботу.
3. Знайдіть MRS в точці 10,1 (використовуючи похідні). Покажіть свою роботу.
4. Чому два методи визначення MRS дають різні відповіді?
5. Який спосіб краще? Чому?

Посилання

Епіграф можна знайти на сторінці 91 переглянутого видання «Основи економічного аналізу» Пола Самуельсона. Ця чудова книга, написана одним з найбільших економістів ^20-го століття, вивела економіку на новий рівень математичної витонченості. Самуельсон не міг вибрати кращу вступну цитату «Математика - це мова», Джей Віллард Гіббс.