2.1: Уподобання

Ключова ідея полягає в тому, що у кожного споживача є набір лайків і антипатій, бажань і смаків, які називаються уподобаннями. Споживчі переваги дозволяють їм порівнювати будь-які дві комбінації або пакети товарів і послуг з точки зору кращих/гірших або однакових. Результат такого порівняння має два результати:

• Строго кращий: споживачеві подобається одна пачка краще, ніж інша.
• Байдуже: споживач однаково задоволений двома пакетами.

З точки зору алгебри, ви можете вважати суворо бажаним як більше, ніж (\(>\)), байдужим як рівний (=).

Так як споживач може порівнювати будь-які дві пачки, то шляхом багаторазового порівняння різних пачок споживач може ранжувати всі можливі комбінації від кращого до гіршого (на думку споживача).

Три аксіоми

Зроблено три основні припущення щодо переваг для забезпечення внутрішньої послідовності:

1. Повнота: споживач може порівняти будь-які зв'язки і надати бажане або байдуже судження.
2. Рефлексивність: ця умова ідентичності говорить про те, що споживач байдужий при порівнянні зв'язки з собою.
3. Транзитивність: ця умова визначає впорядковане співвідношення між пучками, так що якщо пучок A є кращим для пучка B, а пучок B є кращим для пучка C, то пучок A повинен бути кращим для пучка C.

Повнота і рефлексивність легко приймаються. Транзитивність, з іншого боку, суперечлива. Як питання чистої логіки, ми очікуємо, що споживач зробить послідовні порівняння. Однак на практиці споживачі можуть робити неперехідний або непослідовний вибір.

Приклад неперехідності: Ви стверджуєте, що любите кокс краще, ніж Pepsi, Pepsi краще, ніж RC, і RC краще, ніж кокс. Остання претензія не узгоджується з першими двома. Якщо кокс б'є Pepsi і Pepsi б'є RC, то Кокс повинен дійсно бити RC!

У математиці числа є перехідними по відношенню до операторів порівняння більше, менше або дорівнює. Оскільки 12 більше 8, а 8 більше 3, явно 12 більше, ніж 3.

Спортивні результати, однак, не схожі на математику. Результати ігор можуть легко дати неперехідні результати. Мічиган може перемогти Індіану, і в наступній грі Індіана може перемогти Айову, але мало хто стверджує, що два результати гарантують, що Мічиган виграє, коли він грає в Айові.

Коли ми припускаємо, що переваги є перехідними, це означає, що споживач може ранжувати зв'язки без будь-яких протиріч. Це також означає, що ми можемо визначити вибір споживача між двома пакетами на основі відповідей на попередні порівняння.

Відображення налаштувань за допомогою кривих байдужості

Уподобання споживача можна розкрити, зробивши їй вибір між пучками. Ми можемо описати переваги споживача картою байдужості, яка складається з кривих байдужості.

Єдина крива байдужості - це сукупність комбінацій, які дають рівне задоволення. Якщо дві точки лежать на одній кривій байдужості, це означає, що споживач бачить ці два пучка як зав'язані — ні один не кращий, ні гірший за інший.

Єдина крива байдужості та ціла карта байдужості можуть бути сформовані шляхом того, щоб споживач вибирав між альтернативними пачками товарів. Ми можемо продемонструвати, як це працює на конкретному прикладі.

КРОК Відкрийте книгу Excel Preferences.xls, прочитайте аркуш вступу, а потім перейдіть до розкриття аркуша, щоб побачити, як параметри можуть бути відображені та крива байдужості виявлена.

КРОК Почніть з натискання кнопки. Для зв'язки B введіть 4, потім кому (,), потім 3, потім натисніть кнопку ОК.

Ми використовуємо позначення пари координат так 4,3 ідентифікує комбінацію, яка має 4 одиниці добра на осі х і 3 одиниці товару на осі y.

На аркуші записуються зв'язки, які порівнюються у стовпцях A та B та результат у стовпці C. Вибір здійснюється віртуальним споживачем, чиї невідомі переваги знаходяться на комп'ютері. Попросивши віртуального споживача зробити ряд порівнянь, ми можемо виявити приховані переваги у вигляді кривої байдужості та карти байдужості.

Зверніть увагу, що Excel відображає точку 4,3 на діаграмі. Зелений квадрат означає, що споживач вибрав зв'язку Б. Це означає, що 3,3 і 4,3 не знаходяться на одній кривій байдужості.

КРОК. Натисніть кнопку ще раз. Запропонуйте споживачеві вибір між 3,3 і 2,3.

Цього разу споживач вибрав пачку А і на графіку був поміщений червоний трикутник, що означає, що точка 3,3 строго краща точці 2,3.

Ці два варіанти ілюструють ненаситність. Це означає, що споживач не може бути насичений (або заповнений), тому більше завжди краще. Комбінація 4,3 віддається перевагу 3,3, що є кращим 2,3, оскільки добре\(x_{2}\) тримається постійною при 3 і цей споживач ненаситний, вважаючи за краще більше\(x_{1}\) хорошого менше.

Щоб виявити криву байдужості цього споживача, ми повинні запропонувати більш жорсткий вибір, де ми даємо більше одного блага і менше іншого.

КРОК. Натисніть кнопку ще раз. Цього разу пропонують споживачеві вибір між 3,3 і 4,2.

Споживач вирішив, що 3,3 краще. Це розкриває важливу інформацію про переваги споживача. При 3,3 споживачеві подобається ще одна одиниця\(x_{1}\) менше, ніж втрата однієї одиниці\(x_{2}\).

КРОК Натисніть кнопку ще кілька разів, щоб з'ясувати, де знаходиться точка беззбитковості споживача з точки зору того, скільки\(x_{2}\) потрібно, щоб збалансувати виграш від додаткової одиниці\(x_{1}\). Запропонуйте 4,2.5, а потім спробуйте забрати менше хороших 2, таких як 2.7 або 2.9. Як тільки ви знайдете точку, де сума\(x_{2}\) відібраного точно врівноважує виграш в\(x_{1}\) одній одиниці (від 3 до 4), ви розташували дві точки на одній кривій байдужості. Якщо важко побачити точки на графіку, скористайтеся елементом керування Zoom, щоб збільшити екран (скажімо, на 200%).

Слід виявити, що цей споживач байдужий між зв'язками 3,3 і 4,2,9.

КРОК. Тепер натисніть кнопку.

Сто парних порівнянь проводиться між 3,3 і випадковим набором альтернатив. Легко побачити, що споживач може порівняти кожну точку на графіку з еталонним пакетом 3,3 і судити про кожну точку як краще, гірше або однаково.

КРОК Натисніть кнопку, щоб відобразити криву байдужості, яка проходить через контрольну точку (3,3), як показано на малюнку 2.1. Ваша версія буде схожа, але не зовсім така ж, як малюнок 2.1, оскільки 100 точок вибираються випадковим чином.

Малюнок 2.1: Виявлення кривої байдужості.

Джерело: Preferences.xls! Розкрити

Крива байдужості показує зв'язки, однакові для цього споживача порівняно з 3,3. Всі зв'язки, за якими споживач байдужий до пачки 3,3, лежать на одній кривій байдужості.

Карта байдужості

Кожна комбінація товарів має криву байдужості через нього. Ми часто відображаємо кілька репрезентативних кривих байдужості на діаграмі, і це називається картою байдужості, як показано на малюнку 2.2.

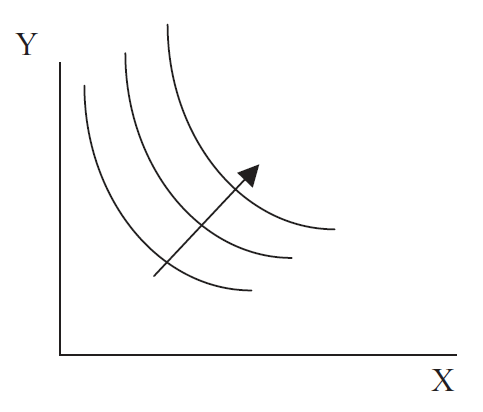Малюнок 2.2: Карта байдужості.

Будь-яка точка на кривій, найвіддаленішій від початку, на малюнку 2.2, є кращою для будь-якої точки під нею, включаючи ті, що знаходяться на двох нижніх кривих байдужості. Стрілка вказує на те, що задоволення збільшується, коли ви рухаєтесь на північний схід до вищих кривих байдужості.

Існує багато (по суті, нескінченності) кривих байдужості, і вони не всі зображуються, коли ми малюємо карту байдужості. Малюємо всього кілька кривих. Ми говоримо, що карта байдужості щільна, а це означає, що через кожну точку є крива.

КРОК Створіть власну карту байдужості, скопіювавши лист Reveal і натиснувши кнопку, потім кнопку, а потім кнопку.

Це поміщає зображення діаграми під діаграмою. Це об'єкт малювання Excel, а не об'єкт діаграми, і він не має заливки.

КРОК Змініть орієнтир на 4,4 в комірці B1 і натисніть кнопку, щоб отримати криву байдужості через нову контрольну точку. Натисніть кнопку.

Це копіює діаграму та вставляє об'єкт малювання поверх першого. Оскільки він не має заливки, він прозорий. Ви можете розділити дві картинки, якщо хочете (клацніть і перетягніть), а потім скасувати хід так, щоб він був поверх першого зображення.

КРОК Додайте ще одну криву байдужості на свою карту, змінивши орієнтир на 5,5 і натиснувши кнопку, потім натиснувши кнопку.

Ви створили карту байдужості з трьома представницькими кривими байдужості. Задоволення збільшується, коли ви рухаєтеся на північний схід до вищих кривих байдужості.

Гранична норма заміщення

Виявивши єдину криву байдужості від віртуального споживача в робочій книзі Excel, ми можемо визначити та працювати з вирішальним поняттям в теорії поведінки споживачів: граничною швидкістю заміщення, або MRS.

MRS - це єдине число, яке говорить нам про готовність споживача обміняти один товар на інший з даного пакету. MRS може бути\(-18\) або\(-0.07\). Уважно читайте і працюйте з Excel, щоб ви дізналися, що ці цифри говорять вам про переваги споживача.

КРОК Поверніться до листа Reveal (з контрольною точкою 3,3) і натисніть кнопку, щоб скопіювати та вставити зображення поточної кривої байдужості під графіком на аркуші Reveal. Тепер натисніть кнопку, щоб отримати нового віртуального споживача з різними уподобаннями, а потім відобразити криву байдужості для цього нового споживача (натиснувши кнопку).

Зверніть увагу, що крива байдужості не така, як вихідна. Це два різних споживача з різними уподобаннями. Ви можете використовувати кнопки, щоб запропонувати нові споживчі пакети, які можна порівняти з 3,3 базовим комплектом, як і раніше.

Ключова ідея тут полягає в тому, що в 3,3 ми можемо виміряти готовність кожного споживача торгувати\(x_{2}\) в обмін на\(x_{1}\).

Спочатку (як показано на малюнку 2.1 і на знятому вами знімку) ми побачили, що споживач був байдужий між 3,3 і 4,2,9. За ще одну одиницю\(x_{1}\) (від 3 до 4) споживач готовий торгувати 0,1 одиниці\(x_{2}\) (від 3 до 2,9). Тоді MRS\(x_{1}\) для\(x_{2}\) від 3,3 до 4,2,9 вимірюється\(\frac{-0.1}{1}\), або\(-0.1\).

З нашим новим віртуальним споживачем MRS на 3,3 - це інше число. Давайте обчислимо його.

КРОК. Приступаємо до листа MRS. Натисніть кнопку. Мало того, що крива байдужості через 3,3 відображається для цього споживача, вона також показує деякі зв'язки, які лежать на цій кривій байдужості. Ми можемо використовувати цю інформацію для обчислення MRS.

Ви можете обчислити MRS в 3,3, дивлячись на перший пакет після 3,3. Скільки споживач\(x_{2}\) готовий відмовитися, щоб отримати на 0,1 більше\(x_{1}\)? Це співвідношення\(\frac{\Delta x_2}{\Delta x_1}\), (звичайне визначення нахилу «підйом над пробігом»), є нахилом кривої байдужості, яка також є MRS.

MRS також можна обчислити як нахил кривої байдужості в точці за допомогою похідних. Замість обчислення\(\frac{\Delta x_2}{\Delta x_1}\) по кривій байдужості від однієї точки до іншої, можна знайти миттєву швидкість зміни в 3,3. Зробимо це пізніше.

Найважливішою концепцією зараз є те, що MRS - це число, яке вимірює готовність споживача торгувати одним товаром для іншого в конкретний момент. Зазвичай ми думаємо про це з точки зору відмови від деяких добра на осі y, щоб отримати більше добра на осі x.

Не потрапляйте в пастку мислення MRS як про застосування до всієї кривої байдужості. Насправді MRS різна в кожній точці кривої. Для типової кривої байдужості, як на малюнку 2.1, MRS стає меншим (в абсолютному значенні), коли ми рухаємося вниз по кривій (коли вона згладжується).

MRS є негативним, оскільки крива байдужості нахилена вниз: зменшення\(x_{2}\) компенсується збільшенням\(x_{1}\). Ми часто скидаємо знак мінус, тому що порівняння негативних чисел може бути заплутаним. Наприклад, скажімо, один споживач має MRS\(-1\) на 3,3, тоді як інший має MRS\(-\frac{1}{3}\) в цей момент. Це правда, що\(-1\) це менша кількість\(-\frac{1}{3}\), ніж, однак, ми використовуємо MRS для позначення крутизни схилу. Таким чином, щоб уникнути плутанини, проводимо порівняння, використовуючи абсолютне значення MRS.

Малюнок 2.3: Порівняння MRS.

На малюнку 2.3 видно, що чим більшим за абсолютним значенням є MRS, тим більше споживач готовий торгувати товаром по осі y на товар на осі x. Таким чином, MRS\(-1\) в 3,3 означає, що крива байдужості має більш крутий нахил в цій точці, ніж якби MRS був\(-\frac{1}{3}\). Ми б сказали, що MRS більше,\(-1\) ніж\(-\frac{1}{3}\) навіть якщо\(-1\) це менша кількість, ніж\(-\frac{1}{3}\) тому, що ми дивимося лише на абсолютне значення MRS.

Фанкі переваги та їх криві байдужості

Ми можемо зобразити найрізноманітніші переваги з картами байдужості. Ось кілька прикладів.

Приклад 1: Ідеальні замінники - постійний нахил (MRS)

Якщо споживач сприймає дві речі як ідеально замінні, це означає, що вони можуть отримати таке ж задоволення, замінивши одну іншою.

Подумайте про наявність однієї п'ятидоларової купюри та п'яти однодоларових купюр (до тих пір, поки ми не говоримо про купюри на кілька сотень доларів). Якщо споживач не дбає про те, щоб мати 10 доларів як одну десятидоларову купюру, одну п'ятидоларову купюру та п'ять однодоларових купюр або десять однодоларових купюр, то крива байдужості є прямою лінією, як показано на малюнку 2.4.

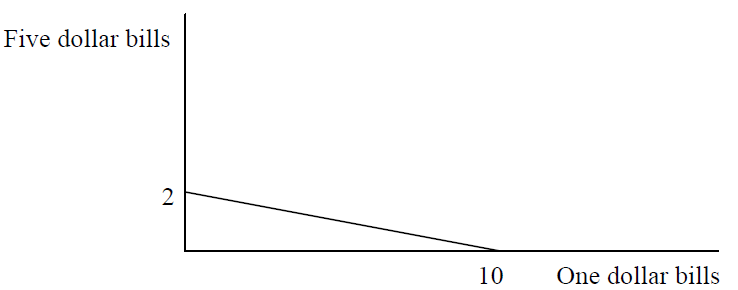Малюнок 2.4: Ідеальні замінники.

Ви можете стверджувати, що тут є неподільність, і насправді є лише 3 точки, які не повинні бути з'єднані лінією, але ключова ідея полягає в тому, що крива байдужості є прямою лінією у випадку ідеальних замінників. Він має постійну MRS (нахил лінії є\(-\frac{1}{5}\)), на відміну від типової кривої байдужості, де MRS падає (в абсолютному значенні) при русі вниз по кривій.

Приклад 2: Ідеальні доповнення - L-образні криві байдужості

Полярна протилежність ідеальних замінників є ідеальними доповненнями. Припустимо, товари в питаннях повинні використовуватися певним чином, не маючи місця для будь-якої гнучкості взагалі, як автомобілі та шини. Для роботи автомобіля потрібно чотири шини. Маючи всього три шини, машина нічого не варта. Ігнорування запасних, наявність більше чотирьох шин вам не допоможе, якщо у вас все ще є всього один автомобіль.

Малюнок 2.5 ілюструє карту байдужості для цієї ситуації. У ньому йдеться про те, що вісім шин з одним автомобілем дають таке ж задоволення, як чотири шини з одним автомобілем. У ньому також сказано, що вісім шин і двох автомобілів віддають перевагу чотирьом шинам і одному автомобілю (або восьми шин і одному автомобілю), оскільки середня Г-подібна крива байдужості (\(I_{1}\)) далі від походження, ніж найнижча крива байдужості (\(I_{0}\)).

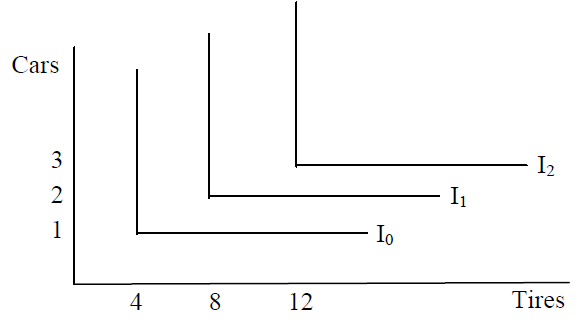Малюнок 2.5: Ідеальні доповнення.

Зверніть увагу, як звичайна крива байдужості лежить між двома крайнощами ідеальних замінників (прямі лінії) і досконалими доповненнями (Г-подібними). Таким чином, типова крива байдужості відображає рівень замінності між товарами, який є більш ніж досконалим доповненням (один товар взагалі не може замінити інший), але менше, ніж досконалі замінники (один товар може зайняти місце іншого без втрати задоволення).

Приклад 3: Bads

Що робити, якщо один з товарів насправді поганий, те, що знижує задоволення, коли ви споживаєте більше його, як забруднення? На малюнку 2.6 показана карта байдужості в даному випадку.

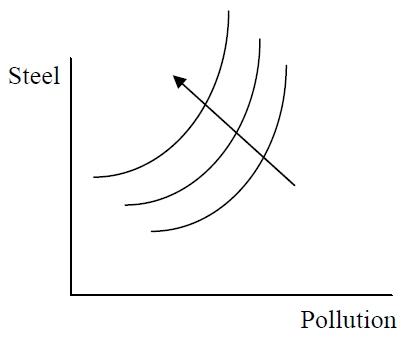Малюнок 2.6: Буси.

Уздовж будь-якої з кривих байдужості більше сталі та більше забруднення однаково задовольняють, оскільки забруднення - це погано, що скасовує додатковий товар від сталі. Стрілка вказує на те, що задоволення збільшується, рухаючись на північний захід, до вищих кривих байдужості.

Приклад 4: Нейтральні товари

Що робити, якщо споживач вважає, що щось не є ні хорошим, ні поганим? Тоді це нейтральне благо і карта байдужості виглядає як Рисунок 2.7.

Горизонтальні криві байдужості для нейтрального блага на осі х на малюнку 2.7 говорять вам, що споживач байдужий, якщо пропонується більше X. Стрілка вказує на те, що задоволення зростає, коли ви рухаєтесь на північ (тому що Y - це добре і більше його збільшує задоволення).

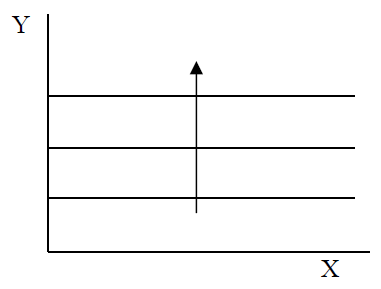Малюнок 2.7: Х - нейтральне благо.

Це лише кілька прикладів того, як різноманітні переваги можна зобразити з картою байдужості. Коли ми хочемо описати загальні, типові переваги, які створюють вниз похилі криві байдужості, як на малюнку 2.2, економісти використовують фразу «добре поводяться переваги».

Ще один технічний термін, який часто використовується в економіці - опуклість, як і в опуклих перевагах. Це означає, що середні точки віддають перевагу крайнощам. На малюнку 2.8 є дві крайні точки, А і В, які з'єднані пунктирною лінією. Будь-яка точка на пунктирній лінії, як C, може бути описана рівнянням\(zA + (1-z)B\), де\(0 < z < 1\) керує позицією С. Це рівняння називається опуклою комбінацією.

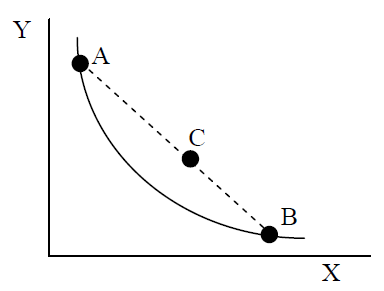Малюнок 2.8: Опуклі налаштування.

Якщо переваги опуклі, то середні точки, такі як C, строго віддають перевагу крайнім точкам, таким як A і B. Опуклість використовується як ще один спосіб сказати, що переваги добре поводяться.

Важливою властивістю, яка виникає з добре поводяться або опуклих уподобань, є зменшення MRS. Як пояснювалося раніше, MRS змінюється по кривій байдужості і застосовується до певної точки (а не до всієї кривої). MRS почнеться великим (в абсолютному значенні) у верхньому лівому куті, як точка А на малюнку 2.8, і стане меншим, коли ми рухаємося вниз по кривій байдужості до точки B. Це має здоровий глузд. Споживач охоче хоче торгувати багато Y для X (тому MRS є високим за абсолютним значенням), коли у нього багато Y і мало X. Коли суми змінюються, наприклад, точка B, невелика MRS означає, що він готовий відмовитися від дуже мало Y (оскільки у нього його мало) за більше X (яких у нього вже багато).

Криві байдужості відображають параметри

Уподобання, симпатії та антипатії споживача можуть бути виявлені або розкриті, попросивши споживача вибрати між парами пучків. Крива байдужості - це той набір пучків, який споживач вважає однаково задовольняючим.

MRS - це єдине число, яке вимірює готовність споживача обміняти один товар на інший в конкретному пункті. Якщо MRS високий (в абсолютному значенні), крива байдужості крута в цій точці, і споживач готовий торгувати багато Y для трохи більше X.

Стандартні, добре поводяться переваги дають набір плавних дуг (на зразок рис. 2.2), але існує безліч інших форм, які зображують переваги для різних видів товарів і взаємозв'язок між товарами.

Вправи

1. Що таке MRS в будь-який момент, якщо X є нейтральним благом? Поясніть чому.
2. Якби добро на осі y було нейтральним добром, а інше - звичайним добром, то як виглядала б карта байдужості. Скористайтеся інструментами малювання Word, щоб намалювати графік цієї ситуації.
3. Якщо переваги добре поводяться, то криві байдужості не можуть перетинатися. Скористайтеся малюнком 2.9, щоб допомогти вам створити пояснення того, чому це твердження має бути правдою. Зверніть увагу, що точка С має більше X і Y, ніж точка A, таким чином, за ненаситністю, C потрібно віддавати перевагу A. Ключ до захисту позову полягає в припущенні про транзитивність.

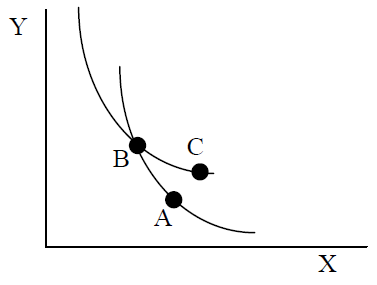   Малюнок 2.9: Неможлива карта байдужості.

4. Припустимо, ми вимірюємо MRS споживача A і B в тій же точці і знайдемо, що\(MRS_{A} = - 6\) і\(MRS_{B} = - 2\). Що можна сказати про переваги A і B на даний момент?

Посилання

Епіграф взято зі сторінки 26 Мікроекономічної теорії К.Е. Фергюсона (переглянуте видання, 1969), популярного мікротексту в 1960-х і 1970-х роках. У передмові Фергюсон писав: «Це підручник; його зміст взято з загального надбання економічної літератури. Звичайні теми трактуються звичайними способами; і реальних інновацій немає». Можливо, але Фергюсон прийняв набагато більш математичне уявлення і додав зміст, включаючи загальну теорію рівноваги, що зробило його книгу іншою і важливою.