Основна ідея теорії споживчої поведінки проста: враховуючи бюджетні обмеження, споживач купує комбінацію товарів і послуг, яка максимізує задоволення, яке захоплюється функцією корисності. Змінюючи ціну конкретного товару, за інших рівних умов (все інше тримається постійним), ми виведемо криву попиту на цей товар.
Налаштування та вирішення проблеми максимізації корисності споживача займає деякий час. Будемо діяти повільно і обережно. Цей розділ присвячений обмеженню бюджету та тому, як вони змінюються при зміні цін або доходів.
Те, що можна собі дозволити, очевидно, є ключовим фактором прогнозування поведінки покупки, але це лише частина історії. Тільки з обмеженням бюджету ми не можемо відповісти на питання про те, скільки споживач хоче придбати кожен продукт, оскільки ми не включаємо жодної інформації про корисність, отриману споживанням. Після того, як ми зрозуміємо обмеження бюджету, ми будемо моделювати лайки та антипатії споживача. Потім ми можемо поставити обмеження та корисні компоненти разом і вирішити модель.
Бюджетне обмеження у формі рівняння
Обмеження бюджету можна виразити математично так:
\(p_{1}x_{1} + p_{2}x_{2} \le m\)
Це рівняння говорить про те, що сума суми витрачених грошей на благо\(x_{1}\), яка є ціною в\(x_{1}\) рази більше кількості придбаних одиниць, або\(p_{1}x_{1}\), і сума, витрачена на благо\(x_{2}\)\(p_{2}x_{2}\), тобто повинна бути менше, ніж або дорівнює сумі доходу, м (за гроші), споживач має в наявності.
Очевидно, що модель була б більш реалістичною, якби у нас було багато продуктів, які споживач міг би купити, але виграш в реалістичності не варто додаткових витрат на обчислювальну складність. Ми можемо легко дозволити\(x_{2}\) стояти за «всі інші товари».
Ще одне спрощення дозволяє перетворити нерівність у рівнянні до суворої рівності. Будемо вважати, що часу не проходить, тому немає заощаджень (не витрачаючи весь наявний дохід) або запозичень. Іншими словами, споживач живе за наносекунду - купуючи, споживаючи та помираючи в ту саму мить. Знову ж таки, це припущення не таке суворе, як спочатку виглядає. Ми можемо включити заощадження та запозичення в цю модель, визначивши одне благо як теперішнє споживання, а інше - як майбутнє споживання. Ми будемо використовувати цю техніку моделювання в майбутньому додатку.
Оскільки ми знаємо, що завжди будемо витрачати весь свій дохід, рівняння обмеження бюджету можна записати зі знаком рівності, ось так
\(p_{1}x_{1} + p_{2}x_{2} = m\)
Оскільки ми хочемо намалювати графік, ми можемо записати у вигляді рівняння прямої (\(y = mx + b\)) за допомогою невеликої алгебраїчної маніпуляції:
Перехоплення\(m/p_{2}\), трактується як максимальна сума\(p_{2}\) того, що споживач може собі дозволити. Купуючи немає\(x_{1}\) і витрачаючи весь дохід на\(x_{2}\), найбільше споживач може купити\(m/p_{2}\) одиниці хорошого 2.
Схил\(-p_{1}/p_{2}\) також має зручну інтерпретацію: У ньому вказується швидкість, з якою ринок вимагає від споживача відмовитися,\(x_{2}\) щоб придбати\(x_{1}\). Це легко побачити, якщо ви пам'ятаєте, що нахил лінії - це просто підйом (\(\Delta x_{2}\)) над пробігом (\(\Delta x_{1}\)). Потім,
КРОК Відкрийте книгу Excel BudgetConstraint.xls, прочитайте Інтро аркуш, а потім перейдіть до Властивості аркуша, щоб побачити обмеження бюджету.
На малюнку 1.1 показана організація листа. Як бачите, споживач вибирає обсяги товарів 1 і 2 для покупки, враховуючи ціни і дохід.
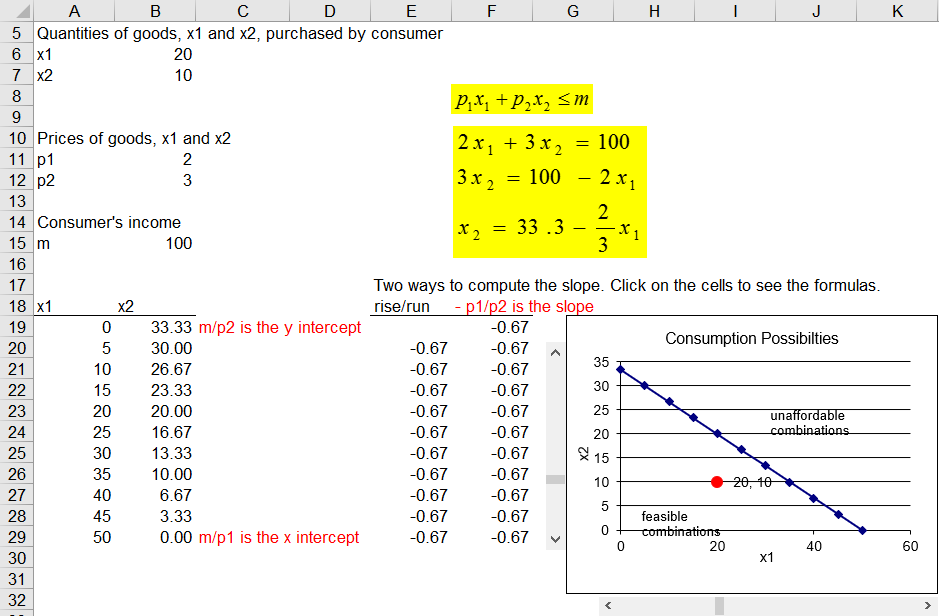
Малюнок 1.1: Бюджетна лінія.
Джерело: BudgetConstraint.xls! Властивості
При\(p_{1}\) = $2/одиницю,\(p_{2}\) = $3/одиницю і\(m\) = $100 можна обчислити рівняння бюджетної лінії.
КРОК Натисніть на смуги прокрутки, щоб побачити червону крапку (яка представляє розшарування споживання), переміщайтеся по графіку.
Переписуючи рівняння бюджетних обмежень у вигляді лінії, а потім графікуючи його, ми маємо геометричне уявлення про можливості споживання споживача. Всі пункти всередині або на бюджетній лінії здійсненні. Окуляри на північний схід від бюджетної лінії непідйомні.
Натиснувши смуги прокрутки, ви можете легко побачити, що споживач має багато можливих точок. Велике питання полягає в тому, яка з цих багатьох доступних комбінацій буде обрана? Ми не можемо відповісти на це питання лише обмеженням бюджету. Потрібно знати, наскільки споживачеві подобаються два товари. Обмеження - це просто можливі варіанти.
Зміни у рядку бюджету — зведення та зрушення
КРОК. Перейдіть до листа змін.
Ідея тут полягає в тому, що зміни цін призводять до того, що бюджетна лінія обертається або обертається, змінюючи нахил, але зберігаючи один із перехоплювачів однаковим. Зверніть увагу, що зміни доходів дають інший результат, зміщуючи бюджетну лінію всередину або назовні, залишаючи нахил незмінним.
КРОК Щоб побачити, як крутиться бюджетна лінія, поекспериментуйте з осередком К9 (ціна хороша 1). Змініть його з 2 на 5.
Графік змінюється, щоб показати нову бюджетну лінію. Бюджетна лінія оберталася навколо перехоплення y, тому що якби споживач вирішив витратити весь дохід на\(x_{2}\), сума, яку можна було б придбати, залишиться колишньою.
Якщо знизити ціну хорошого 1, бюджетна лінійка розгойдується. Підтвердіть, що це правда.
КРОК Зміна осередку К10 змінює бюджетну лінію, змінюючи ціну хорошого 2. Ще раз змініть значення в комірці, щоб побачити ефект на бюджетній рядку.
КРОК Далі натисніть кнопку, щоб повернути лист до початкових значень і попрацювати з осередком К13. Скоротіть дохід навпіл. Ефект різко відрізняється. Замість того, щоб обертатися, бюджетна лінія змістилася. Ухил залишається колишнім, оскільки ціни не змінилися. Збільшення доходів зміщує бюджетну лінію.
На цьому основи бюджетних рядків закінчуються. Варто витратити трохи часу, граючи з осередками К9, К10 і К13, щоб посилити розуміння того, як рухаються бюджетні лінії, коли відбувається зміна ціни або доходу. Ці шоки будуть використані знову, коли ми вивчимо, як змінюється оптимальне рішення споживача при зміні цін або доходу.
Запам'ятайте ключовий урок: Зміна ціни обертає бюджетну лінію, але зміна доходу зміщує її.
Funky Бюджетні лінії
На додаток до стандартного, лінійного бюджетного обмеження, існує ще багато більш складних сценаріїв, з якими стикаються споживачі. Щоб дати вам смак можливостей, давайте розглянемо два приклади.
КРОК. Приступаємо до нормування аркуша.
У цьому прикладі, крім звичайного обмеження доходу, споживачеві допускається максимальна кількість одного з товарів. Таким чином, було додано друге обмеження (вертикальна лінія). Коли максимум вище\(x_{1}\) перехоплення (50 одиниць), це друге обмеження вважається необов'язковим. Як видно з аркуша, коли обмеження максимальної суми є обов'язковим, воно скидає частину бюджетного рядка.
КРОК Змініть комірку E13, щоб побачити, як зміна нормованої суми впливає на бюджетні обмеження.
У міру збільшення суми субсидії горизонтальна лінія продовжується. Спускається вниз похила частина має такий же ухил, але вона виштовхується назовні,
КРОК. Переходимо до листа субсидій.
У цьому прикладі, крім звичайного обмеження доходу, споживачеві надається субсидія у вигляді фіксованої суми товару.
Харчові талони - класичний приклад субсидій. Припустимо, споживач має 100 доларів доходу, але дається 20 доларів в продовольчих талонів (які можна витратити тільки на їжу), а їжа (\(x_{1}\)) коштує 2 долари за одиницю. Тоді бюджетне обмеження має горизонтальний відрізок від 0 до 10 одиниць продовольства, оскільки найбільше\(x_{2}\) (інші товари), які можна придбати, залишається при\(m\)/\(p_{2}\)від 0 до 10 одиниць їжі (оскільки продовольчі талони не можуть бути використані для купівлі інших товарів).
КРОК Змініть осередок Е13, щоб побачити, як зміна заданої кількості їжі (яка є доларовою сумою продовольчих талонів, розділених на ціну їжі) впливає на бюджетні обмеження.
Резюме: Можливості споживання
Бюджетне обмеження є ключовою складовою проблеми оптимізації, що стоїть перед споживачем. Графік обмеження дозволяє нам побачити варіанти споживача. Подібно до того, як кордон виробничих можливостей говорить нам, що може виробляти економіка, обмеження бюджету показує, що споживач може купити. Будь-яка комбінація на або під обмеженням є можливим варіантом. Окуляри поза обмеженням недосяжні.
Зміна цін по-іншому впливає на обмеження, ніж зміна доходу. Якщо ціни змінюються, бюджетна лінія обертається, коливається і обертається (виберіть улюблене слово і запам'ятайте його) навколо перехоплення. Зміна доходу, однак, зміщує лінію (поза або в) і залишає схил незмінним.
Основним бюджетним обмеженням є лінія, але є багато інших сценаріїв, з якими стикаються споживачі, в яких обмеження може бути зламаним або нелінійним. Субсидії (наприклад, продовольчі талони) можуть бути включені в базову модель. Ця гнучкість є однією з потужних особливостей теорії поведінки споживачів.
Обмеження - лише одна частина проблеми оптимізації споживача. Бажаність товарів і послуг, також відомих як смаки та уподобання, є ще однією важливою частиною. Наступний розділ пояснює, як ми моделюємо задоволення від споживання товарів і послуг.
вправи
Використовуйте Excel, щоб створити діаграму бюджетного обмеження, яка базується на наступній інформації: m = $100 і\(p_{2}\) = $3/одиниця, але\(p_{1}\) = $2/одиниця для перших 20 одиниць і $1/одиниця після цього. Скопіюйте діаграму та вставте її в документ Word.
Якщо благо на осі y вільне, як виглядає бюджетне обмеження?
Яке поєднання потрясінь може зробити нову бюджетну лінію повністю всередині і крутіше початкової бюджетної лінії?
Що станеться з бюджетною лінією, якщо всі ціни і доходи подвоюються?
Посилання
Епіграф цієї глави можна знайти на сторінці 48 переглянутого видання Мілтона Фрідмана його тексту теорії цін. Книга по суті є його конспектами лекцій зі знаменитого курсу теорії цін на дві чверті, який Фрідман читав протягом багатьох років в Чиказькому університеті. Цікаво побачити, як тоді навчали Micro, особливо, наскільки мало уваги приділялося математиці. Проблеми в додатку B справді провокують думки.
кнопку, щоб повернути лист до початкових значень і попрацювати з осередком К13. Скоротіть дохід навпіл. Ефект різко відрізняється. Замість того, щоб обертатися, бюджетна лінія змістилася. Ухил залишається колишнім, оскільки ціни не змінилися. Збільшення доходів зміщує бюджетну лінію.