2: Градієнти тиску

Last updated
Save as PDF

Page ID: 37247

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

З класу географії середньої школи ви можете пам'ятати, що «повітря має тенденцію протікати від високого тиску до низького тиску». Щоб зрозуміти, чому це відбувається, важливо усвідомити, що гази (але також рідини) чинять силу на своє оточення через тепловий рух молекул. Ця сила знаходиться в усіх напрямках, так як тепловий рух йде у всіх напрямках. Тиск (\(p\)) - це просто сила (\(F\)) на одиницю площі (\(A\)):

\[ p=\dfrac{F}{A} \label{2.1}\]

Для газів існує дуже проста приблизна залежність між тиском, щільністю та температурою газу: Закон ідеального газу. Хоча такої елегантної формули для рідин не існує, Міжнародне рівняння стану використовується для зв'язку тиску, температури, солоності (концентрації солі) та щільності морської води. Якщо з якої-небудь причини (температура, щільність, солоність) тиск в одній точці простору відрізняється, ніж в сусідній точці, то існує градієнт тиску. Тепер розглянемо ділянку рідини з нескінченно малою товщиною\(dx\) і площею поверхні,\(A\) як показано на малюнку нижче, де є горизонтальний градієнт тиску (\(dp/dx\)), з більшим тиском праворуч, ніж зліва.

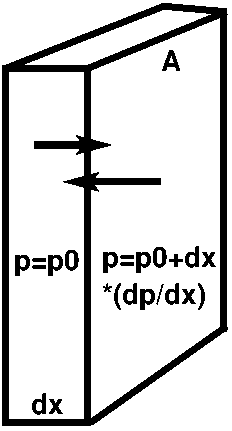
Рідина з правого боку посилки штовхає посилку вліво, тоді як рідина на лівій стороні посилки штовхає її вправо. Однак через градієнт тиску поштовх вліво трохи важче, ніж поштовх вправо. Таким чином, виникає чиста сила на посилку:

\[ F= A * \left[ p_o - \left(p_o+dx * \left(\dfrac{dp}{dx}\right) \right) \right] = -A * dx * \left( \dfrac{dp}{dx} \right) \tag{2.2}\]

Згідно з 2-м законом Ньютона, прискорення становить:

\[\dfrac{dv}{dt} =\dfrac{F}{m} \tag{2.3}\]

і з\(m = \rho * A * dx\), нарешті, отримаємо:

\[\dfrac{dv}{dt} = - \dfrac{\left(\dfrac{dp}{dx}\right)}{\rho} \tag{2.4}\]

Знак мінуса вказує на те, що прискорення знаходиться в протилежному напрямку градієнта тиску, тобто «повітря має тенденцію протікати від високого тиску до низького тиску»; величина прискорення дорівнює градієнту тиску, поділеному на щільність рідини.