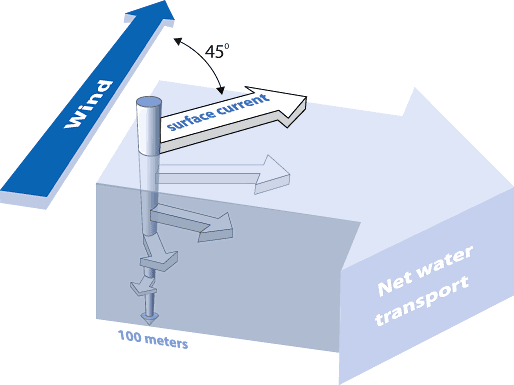
7: Основа вітрової циркуляції - спіраль та транспорти Екмана

Last updated
Save as PDF

Page ID: 37121

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

У розділі 6 було згадано, що великомасштабні течії на поверхні океану рухаються вітром. Це здається досить логічним на перший погляд, але арктичний дослідник Фрідтььоф Нансен помітив щось дивне: айсберги прагнуть дрейфувати під кутом праворуч від переважаючого напрямку вітру. Щоб пояснити це чудове спостереження, Екман (1905) сформулював теорію, яка все ще є наріжним каменем фізичної океанографії. Центральне припущення полягає в тому, що поблизу поверхні океану найбільші відхилення від геустрофічного балансу виникають внаслідок вітрового напруження, що призводить до дифузії імпульсу у вертикальному напрямку. Це означає, що до хорошого наближення горизонтальні рівняння балансу імпульсу\((1.2a)\) і\((1.2b)\) в розділі 1 стають:

\[\dfrac{\left(\dfrac{dp}{dx}\right)}{\rho}=f * v +K_v\dfrac{d^2u}{dz^2} \label{7.1a}\]

\[\dfrac{\left(\dfrac{dp}{dy}\right)}{\rho}=-f * u +K_v\dfrac{d^2v}{dz^2} \label{7.1b}\]

Тепер ми розділимо швидкість вгору на геодестрофічну частину (\(u_g,v_g\)) та агеострофічну швидкість Екмана (\(u_E,v_E\)):

\[\dfrac{\left(\dfrac{dp}{dx}\right)}{\rho}=f * (v_g+v_E) +K_v\dfrac{d^2(u_g+u_E)}{dz^2} \label{7.2a}\]

\[\dfrac{\left(\dfrac{dp}{dy}\right)}{\rho}=-f * (u_g+u_E) +K_v\dfrac{d^2(v_g+v_E)}{dz^2} \label{7.2b}\]

З рівнянь\((5.1a)\) і\((5.1b)\) в розділі 5 ми бачимо, що геастрофічні швидкості скасовуються проти термінів градієнта тиску з лівого боку; термінами\(K_v\dfrac{d^2u_g}{dz^2}\) і\(K_v\dfrac{d^2v_g}{dz^2}\) можна знехтувати. Тому рівняння спрощують:

\[f * v_E =-K_v\dfrac{d^2 u_E}{dz^2} \label{7.3a}\]

\[f * u_E =K_v\dfrac{d^2 v_E}{dz^2} \label{7.3b}\]

які можна переформулювати шляхом підстановки в одне звичайне диференціальне рівняння четвертого порядку:

\[u_E =-\left(\dfrac{K_v}{f}\right)^2 \dfrac{d^4 u_E}{dz^4} \label{7.4}\]

з (реальним) рішенням:

\[u_E = A_1 \cos\left(\sqrt{\dfrac{f}{2K_v}}z+\phi_1\right)e^{\sqrt{\dfrac{f}{2K_v}}z}+A_2 \cos\left(\sqrt{\dfrac{f}{2K_v}}z+\phi_2\right)e^{-\sqrt{\dfrac{f}{2K_v}}z} \label{7.5}\]

Для визначення різних коефіцієнтів використовуємо дві граничні умови:

Безпосередній вплив стресу вітру зникає в глибокому океані:\(u_E \rightarrow 0\) для\(z \rightarrow -\infty\). Тому\(A_2\) має бути рівним\(0\).
У розділі 6 ми стверджували, що близько до розділу океан-атмосфера напруга вітру лінійно пропорційна вертикальному градієнту швидкості; це означає, що якщо вітер дме в зональному (Захід-Схід) напрямку,\(\dfrac{du_E}{dz}=\dfrac{\tau_w}{\rho K_v}\) (рівняння\(6.1\)),\(\dfrac{dv_E}{dz}=0\) для\(z=0\). Це призводить до того\(\phi_1=-\dfrac{\pi}{4}\),\(A_1=\dfrac{\tau_w}{\rho \sqrt{f K_v}}\).

Загалом, у нас є:

\[u_E = \dfrac{\tau_w}{\rho \sqrt{f K_v}} \cos\left(\sqrt{\dfrac{f}{2K_v}}z-\dfrac{\pi}{4}\right)e^{\sqrt{\dfrac{f}{2K_v}}z} \label{7.6a}\]

\[v_E = -\dfrac{K_v}{f}\dfrac{d^2 u_E}{dz^2}=\dfrac{\tau_w}{\rho \sqrt{f K_v}} \sin\left(\sqrt{\dfrac{f}{2K_v}}z-\dfrac{\pi}{4}\right)e^{\sqrt{\dfrac{f}{2K_v}}z} \label{7.6b}\]

Транспорти Екмана на одиницю площі в зональному та меридіональному напрямках відповідно:

\[M_{E,x}=\rho\int_{-\infty}^0 u_E\, dz\]

\[M_{E,y}=\rho\int_{-\infty}^0 v_E\, dz\]

Їх можна обчислити шляхом інтеграції рівнянь\(\ref{7.6a}\) і\(\ref{7.6b}\), але набагато простіше використовувати рівняння\(\ref{7.3a}\) і\(\ref{7.3b}\):

\[\begin{align} M_{E,x} &=\dfrac{K_v \rho}{f}\int_{-\infty}^0 \dfrac{d^2 v_E}{dz^2}\, dz \\[4pt] &=\dfrac{K_v \rho}{f}\left(\dfrac{dv_E}{dz}(z=0)-\dfrac{dv_E}{dz}(z\rightarrow-\infty)\right) \\[4pt] &=0 \label{7.7a} \end{align}\]

\[\begin{align} M_{E,y} &=-\dfrac{K_v \rho}{f}\int_{-\infty}^0 \dfrac{d^2 u_E}{dz^2}\, dz \\[4pt] &=-\dfrac{K_v \rho}{f}\left(\dfrac{du_E}{dz}(z=0)-\dfrac{du_E}{dz}(z\rightarrow-\infty)\right) \\[4pt] &=-\dfrac{\tau_w}{f} \label{7.7b} \end{align}\]

Що все це означає? На поверхні океану,

\[u_E=\dfrac{\tau_w}{\rho \sqrt{2f K_v}} \nonumber\]

\[v_E=-\dfrac{\tau_w}{\rho \sqrt{2f K_v}} \nonumber\]

через рівняння\ ref {7.6a} і\ ref {7.6b}, тобто швидкість Екмана знаходиться під кутом праворуч від напрямку вітру в Північній півкулі (і ліворуч від вітру в Південній півкулі) завдяки силі Коріоліса.\(45^{\circ}\) Заглиблюючись, сила Коріоліса продовжує повертати напрямок потоку далі вправо, тоді як швидкість води зменшується експоненціально з глибиною. Як показано на малюнку нижче (люб'язно NOAA), загальна схема потоку утворює так звану спіраль Екмана. Крім того, Рівняння\(\ref{7.7a}\) і\(\ref{7.7b}\) припускають, що чистий транспорт Екмана знаходиться праворуч від напрямку вітру в Північній півкулі.\(90^{\circ}\)