14.1: Функції декількох змінних

Цілі навчання

• Розпізнати функцію двох змінних і визначити її область і діапазон.
• Намалюйте графік функції двох змінних.
• Намалюйте кілька слідів або кривих рівня функції двох змінних.
• Розпізнати функцію трьох або більше змінних і визначити її рівні поверхні.

Наш перший крок - пояснити, що таке функція більш ніж однієї змінної, починаючи з функцій двох незалежних змінних. Цей крок включає визначення області та діапазону таких функцій та навчання їх графіку. Також розглянуто способи співвіднесення графіків функцій у трьох вимірах до графіків більш звичних плоских функцій.

Функції двох змінних

Визначення функції двох змінних дуже схоже на визначення функції однієї змінної. Основна відмінність полягає в тому, що замість відображення значень однієї змінної зі значеннями іншої змінної ми зіставляємо впорядковані пари змінних в іншу змінну.

Визначення: функція двох змінних

Функція двох змінних\(z=f(x,y)\) відображає кожну впорядковану пару\((x,y)\) в підмножині\(D\) дійсної площини\(R^2\) з унікальним дійсним числом z. \(D\)Множина називається доменом функції. Діапазон\(f\) - це набір всіх дійсних чисел z, який має принаймні одну впорядковану пару,\((x,y)∈D\) таку,\(f(x,y)=z\) як показано на малюнку\(\PageIndex{1}\).

Малюнок\(\PageIndex{1}\): Домен функції двох змінних складається з впорядкованих пар\((x,y)\).

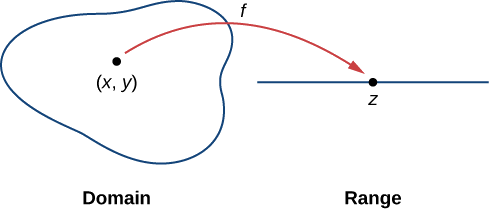
Визначення області функції двох змінних передбачає врахування будь-яких обмежень домену, які можуть існувати. Давайте подивимося.

Приклад\(\PageIndex{1}\): Domains and Ranges for Functions of Two Variables

Знайдіть домен і діапазон кожної з наступних функцій:

1. \(f(x,y)=3x+5y+2\)
2. \(g(x,y)=\sqrt{9−x^2−y^2}\)

Рішення

a Це приклад лінійної функції у двох змінних. Немає значень або комбінацій\(x\) і\(y\) які викликають\(f(x,y)\) бути невизначені, тому область\(f\) є\(R^2\). Щоб визначити діапазон, спочатку виберіть значення для z. Нам потрібно знайти рішення рівняння\(f(x,y)=z,\) або\(3x−5y+2=z.\) Одне таке рішення можна отримати за допомогою першої установки\(y=0\), яка дає рівняння\(3x+2=z\). Рішення цього рівняння полягає в тому\(x=\dfrac{z−2}{3}\), що дає\(\left(\dfrac{z−2}{3},0\right)\) впорядковану пару як розв'язку рівняння\(f(x,y)=z\) для будь-якого значення\(z\). Тому діапазон функції - це всі дійсні числа, або\(R\).

b\(g(x,y)\) Щоб функція мала дійсне значення, величина під квадратним коренем повинна бути невід'ємною:

\[ 9−x^2−y^2≥0. \nonumber \]

Це нерівність можна записати у вигляді

\[ x^2+y^2≤9. \nonumber \]

Тому домен\(g(x,y)\) є\(\{(x,y)∈R^2∣x^2+y^2≤9\}\). Графік цієї множини точок можна описати як диск радіусом 3 з центром у початку координат. Домен включає граничне коло, як показано на наступному графіку.

Малюнок\(\PageIndex{2}\): Домен функції\(g(x,y)=\sqrt{9−x^2−y^2}\) - замкнутий диск радіусом 3.

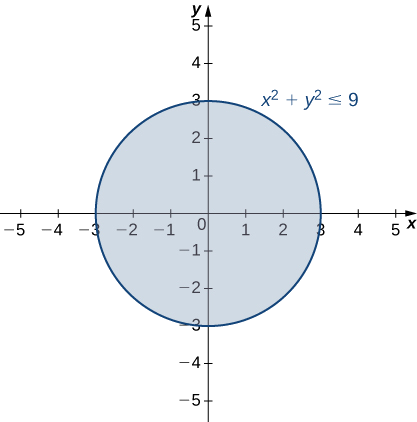
Для визначення діапазону\(g(x,y)=\sqrt{9−x^2−y^2}\) ми починаємо з точки\((x_0,y_0)\) на межі області, яка визначається співвідношенням\(x^2+y^2=9\). Звідси випливає, що\(x^2_0+y^2_0=9\) і

\[ \begin{align*} g(x_0,y_0) =\sqrt{9−x^2_0−y^2_0} \\[4pt] =\sqrt{9−(x^2_0+y^2_0)}\\[4pt] =\sqrt{9−9}\\[4pt] =0. \end{align*}\]

Якщо\(x^2_0+y^2_0=0\) (іншими словами\(x_0=y_0=0)\), то

\[ \begin{align*} g(x_0,y_0) =\sqrt{9−x^2_0−y^2_0}\\[4pt] =\sqrt{9−(x^2_0+y^2_0)}\\[4pt] =\sqrt{9−0}=3. \end{align*}\]

Це максимальне значення функції. З огляду на будь-яке значення\(c\) між\(0\) і\(3\), ми можемо знайти цілий набір точок всередині області\(g\) таких, що\(g(x,y)=c:\)

\[\begin{align*} \sqrt{9−x^2−y^2} =c \\[4pt] 9−x^2−y^2 =c^2 \\[4pt] x^2+y^2 =9−c^2. \end{align*}\]

Так як\(9−c^2>0\), це описує коло радіуса з\(\sqrt{9−c^2}\) центром у початковій точці. Будь-яка точка на цьому колі задовольняє рівнянню\(g(x,y)=c\). Тому діапазон цієї функції може бути записаний в інтервальних позначеннях як\([0,3].\)

Вправа\(\PageIndex{1}\)

Знайдіть домен і діапазон функції\(f(x,y)=\sqrt{36−9x^2−9y^2}\).

Підказка

Визначте набір впорядкованих пар, які не роблять радикальні негативні.

Рішення

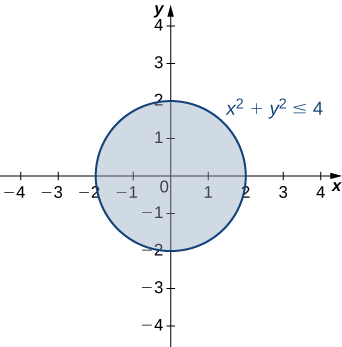
Домен - це\(\{(x, y) | x^2+y^2≤4 \}\) затінене коло, визначене нерівністю\(x^2+y^2≤4\), яка має коло радіуса\(2\) як свою межу. Асортимент\([0,6].\)

Графічні функції двох змінних

Припустимо, ми хочемо, щоб графік функції\(z=f(x,y).\) Ця функція має дві незалежні змінні (\(x\)і\(y\)) і одну залежну змінну\((z)\). При побудові\(y=f(x)\) графіків функції однієї змінної ми використовуємо декартову площину. Ми можемо графікувати будь-яку впорядковану пару\((x,y)\) в площині, і кожна точка на площині має впорядковану пару,\((x,y)\) пов'язану з нею. При функції двох змінних кожна впорядкована пара\((x,y)\) в області функції зіставляється з дійсним числом\(z\). Тому графік функції\(f\) складається з впорядкованих трійок\((x,y,z)\). Графік функції\(z=f(x,y)\) двох змінних називається поверхнею.

Щоб більш повно зрозуміти концепцію побудови набору впорядкованих трійок для отримання поверхні в тривимірному просторі, уявіть собі систему\((x,y)\) координат, що лежить рівно. Тоді кожна точка в області функції f має пов'язане з нею унікальне\(z\) -значення. Якщо\(z\) позитивний, то графічна точка розташована над\(xy\) -площиною, якщо\(z\) негативна, то графічна точка розташована нижче\(xy\) -площини. Множина всіх графічних точок стає двовимірною поверхнею, яка є графіком функції\(f\).

Приклад\(\PageIndex{2}\): Graphing Functions of Two Variables

Створіть графік кожної з наступних функцій:

1. \(g(x,y)=\sqrt{9−x^2−y^2}\)
2. \(f(x,y)=x^2+y^2\)

Рішення

a У прикладі\(\PageIndex{2}\) ми визначили, що домен\(g(x,y)=\sqrt{9−x^2−y^2}\) is\(\{(x,y)∈R^2∣x^2+y^2≤9\}\) і діапазон є\(\{z∈R^2∣0≤z≤3\}\). Коли у\(x^2+y^2=9\) нас є\(g(x,y)=0\). Тому будь-яка точка на колі радіуса,\(3\) центрована на початку координат у\(xy\) -площині, відображає значення\(z=0\) in\(R^3\). Якщо\(x^2+y^2=8\), то\(g(x,y)=1,\) так будь-яка точка на колі радіуса з\(2\sqrt{2}\) центром у початковій точці в\(xy\) -plane відображає\(z=1\) in\(R^3\). Як\(x^2+y^2\) наближається до нуля, значення\(z\) наближається\(3\). Коли\(x^2+y^2=0\), то\(g(x,y)=3\). Це походження в\(xy\) -площині Якщо\(x^2+y^2\) дорівнює будь-якому іншому значенню між\(0\) і\(9\), то\(g(x,y)\) дорівнює деякій іншій константі між\(0\) і\(3\). Поверхня, описана цією функцією, являє собою півкулю з центром у початку з радіусом\(3\), як показано на наступному графіку.

Рисунок\(\PageIndex{3}\): Графік півкулі, представлений заданою функцією двох змінних.

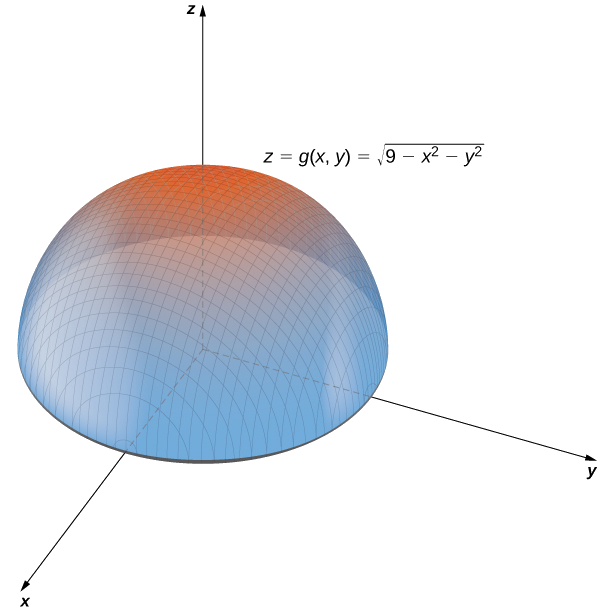
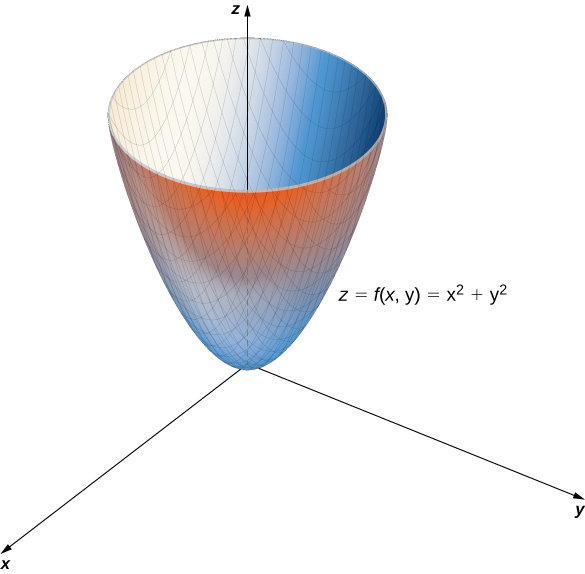
b Ця функція також містить вираз\(x^2+y^2\). Встановивши цей вираз рівним різним значенням, починаючи з нуля, отримаємо кола зростаючого радіуса. Мінімальне значення\(f(x,y)=x^2+y^2\) дорівнює нулю (досягається при\(x=y=0.\). Коли\(x=0\), функція стає\(z=y^2\), а коли\(y=0\), то функція стає\(z=x^2\). Це і є поперечні перерізи графіка, і є параболами. Нагадаємо з Введення в вектори в просторі, що назва графа\(f(x,y)=x^2+y^2\) є параболоїдом. Графік\(f\) відображається на наступному графіку.

Малюнок\(\PageIndex{4}\): Параболоїд - це графік заданої функції двох змінних.

Приклад\(\PageIndex{3}\): Nuts and Bolts

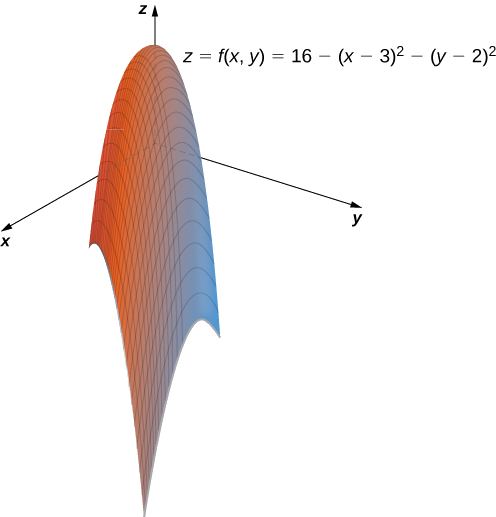
Функція прибутку для виробника обладнання дається

\[f(x,y)=16−(x−3)^2−(y−2)^2, \nonumber \]

де\(x\) - кількість проданих гайок за місяць (вимірюється тисячами) і\(y\) являє собою кількість проданих болтів за місяць (вимірюється тисячами). Прибуток вимірюється тисячами доларів. Намалюйте графік цієї функції.

Рішення

Ця функція є поліноміальною функцією в двох змінних. Домен of\(f\) складається з\((x,y)\) координатних пар, які дають невід'ємний прибуток:

\[ \begin{align*} 16−(x−3)^2−(y−2)^2 ≥ 0 \\[4pt] (x−3)^2+(y−2)^2 ≤ 16. \end{align*}\]

Це диск з радіусом по\(4\) центру\((3,2)\). Подальше обмеження полягає в тому, що обидва\(x\) і\(y\) повинні бути ненегативними. Коли\(x=3\) і\(y=2, f(x,y)=16.\) Зверніть увагу, що можна для будь-якого значення бути нецілим; наприклад, можна продати\(2.5\) тисячу горіхів за місяць. Таким чином, домен містить тисячі точок, тому ми можемо розглянути всі точки всередині диска. Для будь-якого\(z<16\), ми можемо вирішити рівняння\(f(x,y)=16:\)

\[ \begin{align*} 16−(x−3)^2−(y−2)^2 =z \\[4pt] (x−3)^2+(y−2)^2 =16−z. \end{align*}\]

Оскільки\(z<16,\) ми знаємо, що\(16−z>0,\) таким чином попереднє рівняння описує коло з радіусом,\(\sqrt{16−z}\) центрованим у точці\((3,2)\). Отже, діапазон\(f(x,y)\) є\(\{z∈\mathbb{R}|z≤16\}.\) Графік також параболоїд, і цей параболоїд вказує вниз, як показано.\(f(x,y)\)

Малюнок\(\PageIndex{5}\): Графік заданої функції двох змінних також є параболоїдом.

Криві рівня

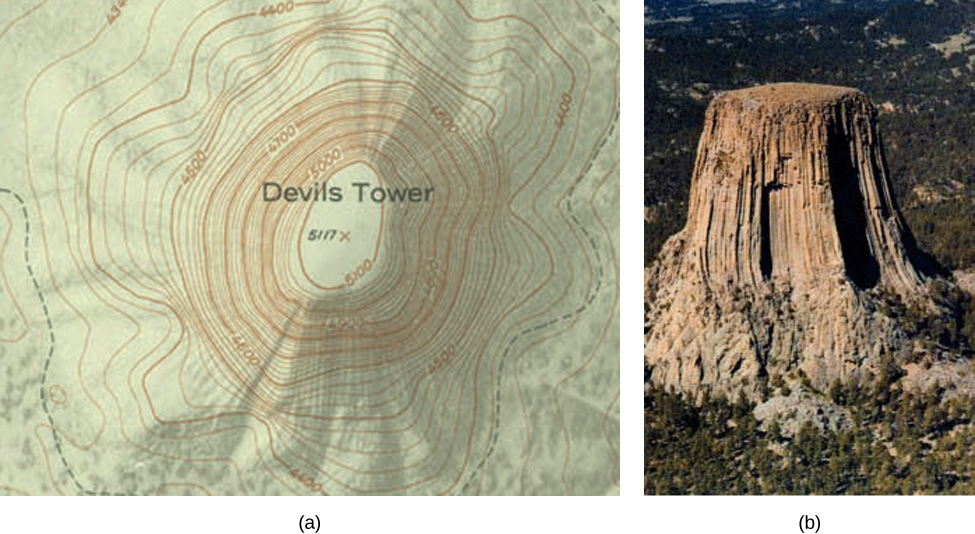
Якщо туристи ходять по міцних стежках, вони можуть використовувати топографічну карту, яка показує, як круто змінюються стежки. Топографічна карта містить вигнуті лінії, які називаються контурними лініями. Кожна лінія контуру відповідає точкам на карті, які мають однакову висоту (рис.\(\PageIndex{6}\)). Крива рівня функції двох змінних\(f(x,y)\) повністю аналогічна контурній лінії на топографічній карті.

Малюнок\(\PageIndex{6}\): (а) Топографічна карта диявольської вежі, Вайомінг. Лінії, які знаходяться близько один до одного, вказують на дуже круту місцевість. (б) Перспективна фотографія вежі Диявола показує, наскільки круті її сторони. Зверніть увагу, що вершина вежі має таку ж форму, як і центр топографічної карти.

Визначення: криві рівня

Враховуючи функцію\(f(x,y)\) та число\(c\) в діапазоні\(f\), крива рівня функції двох змінних для значення визначена\(c\) множиною точок, що задовольняють рівнянню\(f(x,y)=c.\)

Повертаючись до функції\(g(x,y)=\sqrt{9−x^2−y^2}\), ми можемо визначити криві рівня цієї функції. Діапазон -\(g\) замкнутий інтервал\([0,3]\). По-перше, ми вибираємо будь-яке число в цьому замкнутому інтервалі - скажімо,\(c=2\). Крива рівня, відповідна\(c=2\), описується рівнянням

\[ \sqrt{9−x^2−y^2}=2. \nonumber \]

Щоб спростити, квадрат обидві сторони цього рівняння:

\[ 9−x^2−y^2=4. \nonumber \]

Тепер помножте обидві сторони рівняння на\(−1\) і додайте\(9\) до кожної сторони:

\[ x^2+y^2=5. \nonumber \]

Це рівняння описує коло з центром у початку координат з радіусом\(\sqrt{5}\). Використання значень\(c\) між\(0\) і\(3\) дає інші кола, також зосереджені на початку. Якщо\(c=3\), то коло має радіус\(0\), тому він складається виключно з початку. Малюнок\(\PageIndex{7}\) являє собою графік кривих рівня цієї функції, відповідних\(c=0,1,2,\) і\(3\). Зверніть увагу, що в попередньому виведенні можливо, що ми ввели додаткові рішення шляхом квадратизації обох сторін. Тут це не так, оскільки діапазон функції квадратного кореня є невід'ємним.

Рисунок\(\PageIndex{7}\): Криві рівня функції\(g(x,y)=\sqrt{9−x^2−y^2}\), використовуючи\(c=0,1,2,\) і\(3 (c=3\) відповідає початку).

Графік різних кривих рівня функції називається контурною картою.

Приклад\(\PageIndex{4}\): Making a Contour Map

За заданою функцією знайдіть криву рівня\(f(x,y)=\sqrt{8+8x−4y−4x^2−y^2}\), відповідну\(c=0\). Потім створіть контурну карту для цієї функції. Що таке домен і діапазон\(f\)?

Рішення

Для пошуку кривої рівня\(c=0,\) задаємо\(f(x,y)=0\) і вирішуємо. Це дає

\(0=\sqrt{8+8x−4y−4x^2−y^2}\).

Потім ми квадратимо обидві сторони і множимо обидві сторони рівняння на\(−1\):

\(4x^2+y^2−8x+4y−8=0.\)

Тепер ми переставляємо терміни, склавши\(x\) терміни разом і\(y\) терміни разом, і додаємо\(8\) до кожної сторони:

\(4x^2−8x+y^2+4y=8.\)

Далі згрупуємо пари термінів, що містять однакову змінну в дужках, і множник\(4\) з першої пари:

\(4(x^2−2x)+(y^2+4y)=8.\)

Потім заповнюємо квадрат в кожній парі дужок і додаємо правильне значення в праву сторону:

\(4(x^2−2x+1)+(y^2+4y+4)=8+4(1)+4.\)

Далі фактуємо ліву сторону і спрощуємо праву сторону:

\(4(x−1)^2+(y+2)^2=16.\)

Останнім ділимо обидві сторони на\(16:\)

\(\dfrac{(x−1)^2}{4}+\dfrac{(y+2)^2}{16}=1.\label{conteq0}\)

Це рівняння описує еліпс з центром. Графік цього еліпса з'являється на наступному графіку.\((1,−2).\)

Малюнок\(\PageIndex{8}\): Крива рівня функції,\(f(x,y)=\sqrt{8+8x−4y−4x^2−y^2}\) що відповідає\(c=0\)

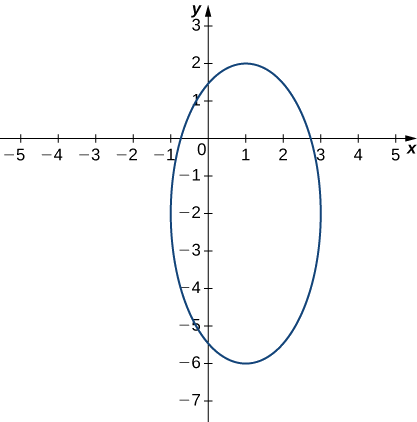
Ми можемо повторити ту саму деривацію для значень\(c\) менше, ніж\(4.\) Тоді, Equation\ ref {conteq0} стає

\(\dfrac{4(x−1)^2}{16−c^2}+\dfrac{(y+2)^2}{16−c^2}=1\)

для довільного значення\(c\). \(\PageIndex{9}\)На малюнку показана контурна карта для\(f(x,y)\) використання значень\(c=0,1,2,\) і\(3\). Коли\(c=4,\) крива рівня є точкою\((−1,2)\).

Малюнок\(\PageIndex{9}\): Контурна карта для функції з\(f(x,y)=\sqrt{8+8x−4y−4x^2−y^2}\) використанням значень\(c=0,1,2,3,\) і\(4\).

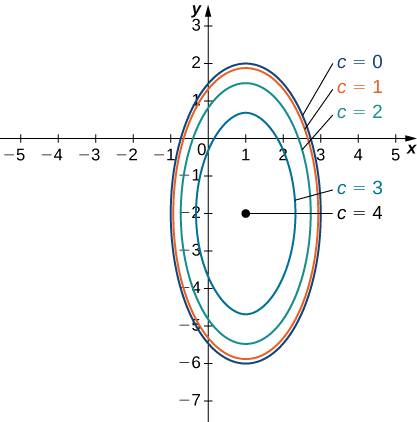
Пошук домену та діапазону

Так як це функція квадратного кореня, то радиканд не повинен бути негативним. Отже, у нас є

\[8+8x−4y−4x^2−y^2\ge 0 \nonumber \]

Визнаючи, що межа області є еліпсом, повторюємо кроки, які ми показали вище, щоб отримати

\[\dfrac{(x−1)^2}{4}+\dfrac{(y+2)^2}{16}\le 1 \nonumber \]

Таким чином, домен\(f\) може бути записаний:\(\big\{ (x,y) \,|\, \frac{(x−1)^2}{4}+\frac{(y+2)^2}{16}\le 1 \big\}.\)

Щоб знайти діапазон,\(f,\) нам потрібно розглянути можливі виходи цієї функції квадратного кореня. Ми знаємо, що вихід не може бути від'ємним, тому нам потрібно перевірити, чи є його вихід коли-небудь\(0.\) З роботи, яку ми завершили вище, щоб знайти криву рівня для\(c = 0,\) ми знаємо, що значення\(f\) є\(0\) для будь-якої точки на кривій цього рівня (на еліпсі,\(\frac{(x−1)^2}{4}+\frac{(y+2)^2}{16}=1\)). Таким чином, ми знаємо, нижня межа діапазону цієї функції є\(0.\)

Визначити верхню межу діапазону функції в цій задачі простіше, якщо попередньо завершити квадрат під радикалом.

\ [\ почати {вирівнювати*} f (x, y) &=\ sqrt {8x−4y−4y−4y−4y^2}\\ [5pt]
&=\ sqrt {8 - 4 (x^2 - 2x\ квадрад) - (y^2 + 4y\ quad)}\\ [5pt]
&=\ sqrt {8 - 4 (x^2 - 2 - 2y\ quad) x +1 - 1) - (y^2 + 4г + 4 - 4)}\\ [5пт]
&=\ sqrt {8 - 4 (x^2 - 2x +1) + 4 - (y^2+ 4y + 4) +4}\\ [5pt]
&=\ sqrt {16 - 4 (x-1) ^2 - (y+2) ^2}\ кінець {вирівнювати*}\]

Тепер, коли ми маємо\(f\) в такому вигляді, ми можемо побачити, наскільки великим може бути радиканд. Оскільки ми віднімаємо два ідеальних квадрата,\(16,\) ми знаємо, що значення радиканд не може бути більшим, ніж\(16.\) У точці\((1, -2),\) ми можемо побачити радиканд буде 16 (оскільки ми будемо віднімати\(0\) з\(16\) цієї точки. Це дає нам максимальне значення\(f\), тобто\(f(1, -2) = \sqrt{16} = 4.\)

Отже, діапазон цієї функції\([0, 4].\)

Вправа\(\PageIndex{2}\)

Знайдіть та графікуйте криву рівня функції,\(g(x,y)=x^2+y^2−6x+2y\) що відповідає\(c=15.\)

Підказка

Спочатку встановлюємо,\(g(x,y)=15\) а потім завершуємо квадрат.

Рішення

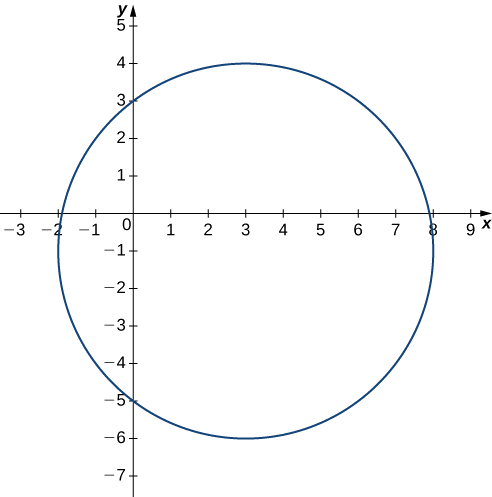
Рівняння кривої рівня можна записати так\((x−3)^2+(y+1)^2=25,\), як це коло з радіусом,\(5\) центрованим на\((3,−1).\)

Ще один корисний інструмент для розуміння графіка функції двох змінних називається вертикальним трасом. Криві рівня завжди графічні\(xy-plane\), але, як випливає з їх назви, вертикальні сліди графуються в\(xz\) - або\(yz\) -площинами.

Визначення: вертикальні сліди

Розглянемо функцію\(z=f(x,y)\) з доменом\(D⊆\mathbb{R}^2\). Вертикальний слід функції може бути як множиною точок, що вирішує рівняння\(f(a,y)=z\) для заданої константи,\(x=a\) так і\(f(x,b)=z\) для заданої константи.\(y=b.\)

Приклад\(\PageIndex{5}\): Finding Vertical Traces

Знайти вертикальні сліди для функції,\(f(x,y)=\sin x \cos y\) що відповідають\(x=−\dfrac{π}{4},0,\) і\(\dfrac{π}{4}\), і\(y=−\dfrac{π}{4},0\), і\(\dfrac{π}{4}\).

Рішення

Перший набір\(x=−\dfrac{π}{4}\) у рівнянні\(z=\sin x \cos y:\)

\(z=\sin(−\dfrac{π}{4})\cos y=−\dfrac{\sqrt{2}\cos y}{2}≈−0.7071\cos y.\)

Це описує косинусний графік на площині\(x=−\dfrac{π}{4}\). Інші значення z відображаються в наступній таблиці.

Вертикальні сліди, паралельні\(xz-Plane\) для функції\(f(x,y)=\sin x \cos y\)

\(c\)	Вертикальне трасування для\(x=c\)
\ (c\)» style="вертикальне вирівнювання: середина; ">\(−\dfrac{π}{4}\)	\ (x = c\)» style="вертикальне вирівнювання: середина; ">\(z=−\dfrac{\sqrt{2}\cos y}{2}\)
\ (c\)» style="вертикальне вирівнювання: середина; "> 0	\ (x = c\)» style="вертикальне вирівнювання: середина; ">\(z=0\)
\ (c\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{π}{4}\)	\ (x = c\)» style="вертикальне вирівнювання: середина; ">\(z=\dfrac{\sqrt{2}\cos y}{2}\)

Аналогічним чином ми можемо замінити\(y-values\) в рівнянні,\(f(x,y)\) щоб отримати сліди в тому,\(yz-plane,\) як зазначено в наступній таблиці.

Вертикальні сліди, паралельні\(yz-Plane\) для функції\(f(x,y)=\sin x \cos y\)

\(d\)	Вертикальне трасування для\(y=d\)
\ (d\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{π}{4}\)	\ (y=d\)» style="вертикальне вирівнювання: середина; ">\(z=\dfrac{\sqrt{2}\sin x}{2}\)
\ (d\)» style="вертикальне вирівнювання: середина; "> 0	\ (y=d\)» style="вертикальне вирівнювання: середина; ">\(z=\sin x\)
\ (d\)» style="вертикальне вирівнювання: середина; ">\(−\dfrac{π}{4}\)	\ (y=d\)» style="вертикальне вирівнювання: середина; ">\(z=\dfrac{\sqrt{2}\sin x}{2}\)

Три сліди в\(xz-plane\) є косинусними функціями; три сліди в\(yz-plane\) є синусоїдними функціями. Ці криві з'являються в місцях перетину поверхні з площинами\(x=−\dfrac{π}{4},x=0,x=\dfrac{π}{4}\) і\(y=−\dfrac{π}{4},y=0,y=\dfrac{π}{4}\) як показано на наступному малюнку.

Рисунок\(\PageIndex{10}\): Вертикальні сліди функції\(f(x,y)\) - це косинусні криві в\(xz-planes\) (a) та синусоїдальних кривих у\(yz-planes\) (b).

Вправа\(\PageIndex{3}\)

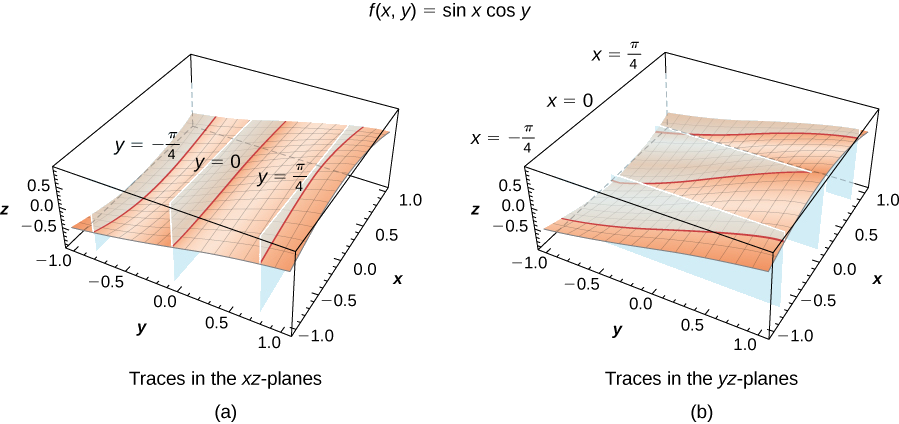
Визначте рівняння вертикального сліду функції,\(g(x,y)=−x^2−y^2+2x+4y−1\) відповідної\(y=3\), і опишіть її графік.

Підказка

\(y=3\)Встановіть рівняння\(z=−x^2−y^2+2x+4y−1\) і завершіть квадрат.

Рішення

\(z=3−(x−1)^2\). Ця функція описує параболу, що відкривається вниз в площині\(y=3\).

Функції двох змінних можуть створювати деякі вражаючі поверхні. На малюнку\(\PageIndex{11}\) показані два приклади.

Рисунок\(\PageIndex{11}\): Приклади поверхонь, що представляють функції двох змінних: (а) поєднання степеневої функції та функції синуса та (б) комбінація тригонометричних, експоненціальних та логарифмічних функцій.

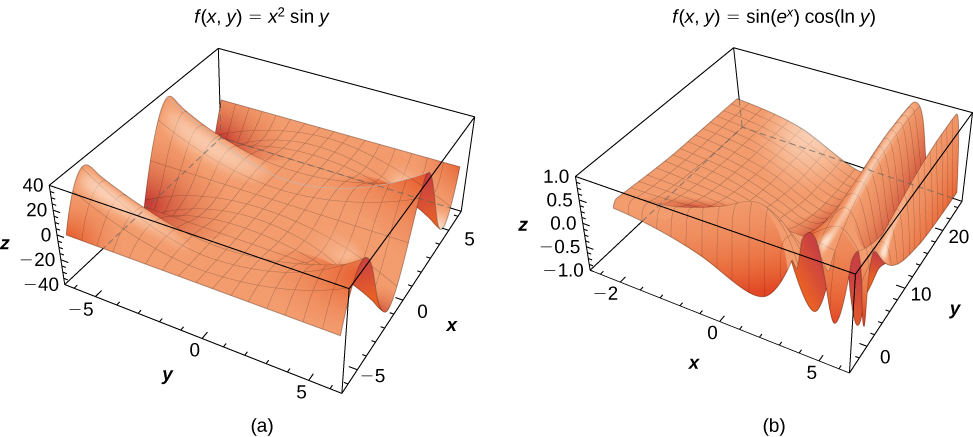
Функції більше двох змінних

Поки ми розглянули тільки функції двох змінних. Однак корисно коротко поглянути на функції більш ніж двох змінних. Два таких приклади

\[ \underbrace{f(x,y,z)=x^2−2xy+y^2+3yz−z^2+4x−2y+3x−6}_{\text{a polynomial in three variables}} \nonumber \]

і

\[g(x,y,t)=(x^2−4xy+y^2)\sin t−(3x+5y)\cos t. \nonumber \]

У першій функції,\((x,y,z)\) являє собою точку в просторі, і функція\(f\) відображає кожну точку в просторі до четвертої величини, наприклад, температури або швидкості вітру. У другій функції,\((x,y)\) може представляти точку в площині, а\(t\) може представляти час. Функція може зіставити точку на площині до третьої величини (наприклад, тиску) в даний момент часу\(t\). Метод знаходження області функції більше двох змінних аналогічний методу для функцій однієї або двох змінних.

Приклад\(\PageIndex{6}\): Domains for Functions of Three Variables

Знайдіть домен кожної з наступних функцій:

1. \(f(x,y,z)=\dfrac{3x−4y+2z}{\sqrt{9−x^2−y^2−z^2}}\)
2. \(g(x,y,t)=\dfrac{\sqrt{2t−4}}{x^2−y^2}\)

Рішення:

а\(f(x,y,z)=\dfrac{3x−4y+2z}{\sqrt{9−x^2−y^2−z^2}}\) Щоб функція була визначена (і була дійсним значенням), повинні дотримуватися дві умови:

1. Знаменник не може бути нулем.
2. Радиканд не може бути негативним.

Поєднання цих умов призводить до нерівності

\[9−x^2−y^2−z^2>0.\nonumber \]

Переміщення змінних на іншу сторону та зворотне нерівність дає домен як

\[domain(f)=\{(x,y,z)∈R^3∣x^2+y^2+z^2<9\},\nonumber \]

який описує кулю радіусу з\(3\) центром у початковій точці. (Примітка: Поверхня кулі не включена в цей домен.)

б\(g(x,y,t)=\dfrac{\sqrt{2t−4}}{x^2−y^2}\) Щоб функція була визначена (і була дійсним значенням), повинні дотримуватися дві умови:

1. Радиканд не може бути негативним.
2. Знаменник не може бути нулем.

Оскільки радиканд не може бути негативним, це означає\(2t−4≥0\), а значить, що\(t≥2\). Так як знаменник не може бути нулем\(x^2−y^2≠0\), або\(x^2≠y^2\), який можна переписати як\(y=±x\), які є рівняннями двох рядків, що проходять через початок. Таким чином, домен\(g\) є

\[ domain(g)=\{(x,y,t)|y≠±x,t≥2\}. \nonumber \]

Вправа\(\PageIndex{4}\)

Знайдіть домен функції\(h(x,y,t)=(3t−6)\sqrt{y−4x^2+4}\).

Підказка

Перевірте значення, які роблять радиканди негативними або знаменниками рівними нулю.

Рішення

\[domain(h)=\{(x,y,t)\in \mathbb{R}^3∣y≥4x^2−4\} \nonumber \]

Функції двох змінних мають криві рівня, які відображаються як криві в\(xy-plane.\) Однак, коли функція має три змінні, криві стають поверхнями, тому ми можемо визначити поверхні рівня для функцій трьох змінних.

Визначення: поверхня рівня функції трьох змінних

Враховуючи функцію\(f(x,y,z)\) та число\(c\) в діапазоні\(f\), рівневу поверхню функції трьох змінних визначено множиною точок, що задовольняють рівнянню\(f(x,y,z)=c.\)

Приклад\(\PageIndex{7}\): Finding a Level Surface

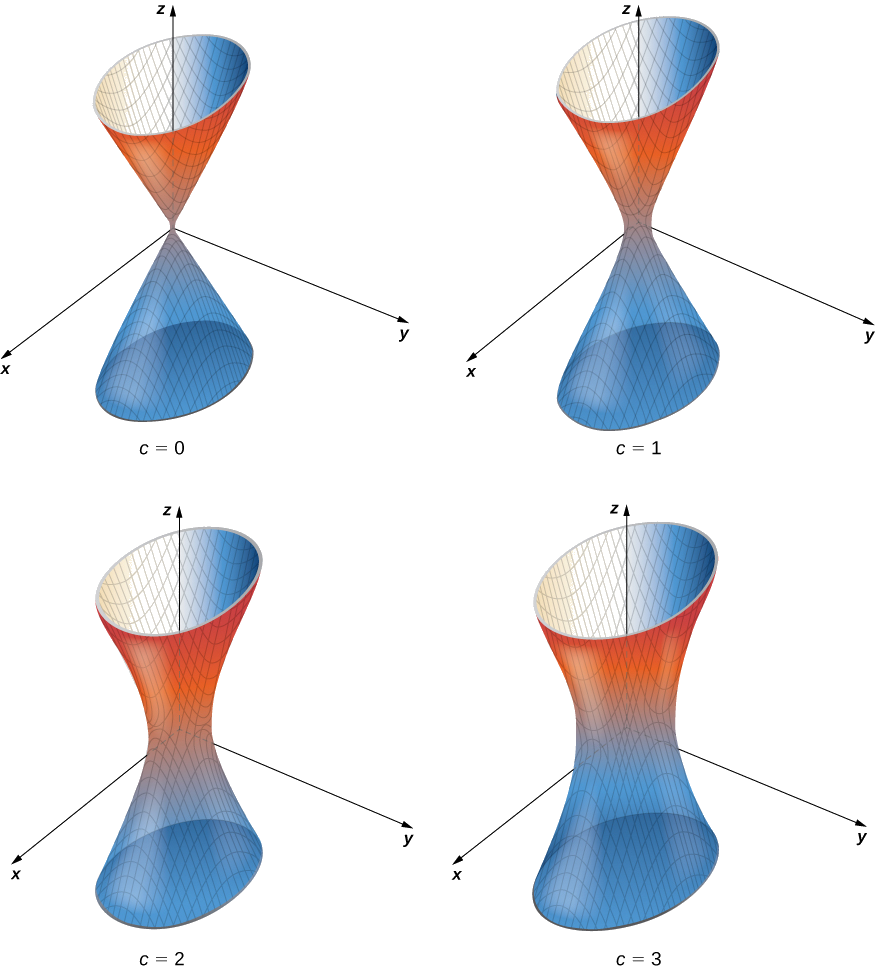
Знайдіть рівну поверхню для функції,\(f(x,y,z)=4x^2+9y^2−z^2\) відповідної\(c=1\).

Рішення

Рівна поверхня визначається рівнянням\(4x^2+9y^2−z^2=1.\) Це рівняння описує гіперболоїд одного листа, як показано на малюнку\(\PageIndex{12}\).

Малюнок\(\PageIndex{12}\): Гіперболоїд одного листа з деякими його рівними поверхнями.

Вправа\(\PageIndex{5}\)

Знайти рівняння рівняння поверхні функції

\[ g(x,y,z)=x^2+y^2+z^2−2x+4y−6z \nonumber \]

відповідність\(c=2,\) і описати поверхню, якщо це можливо.

Підказка

Встановити\(g(x,y,z)=c\) і завершити квадрат.

Рішення

((x−1) ^2+ (y+2) ^2+ (z−3) ^2=16\) описує сферу радіуса з\(4\) центром у точці\((1,−2,3).\)

Резюме

• Графік функції двох змінних є поверхнею в\(\mathbb{R}^3\) і може бути вивчений за допомогою кривих рівня та вертикальних слідів.
• Набір кривих рівня називається картою контурів.

Ключові рівняння

• Вертикальний трасування

\(f(a,y)=z\)для\(x=a\) або\(f(x,b)=z\) для\(y=b\)

• Поверхня рівня функції трьох змінних

\(f(x,y,z)=c\)

Глосарій

контурна карта

графік кривих різних рівнів заданої функції\(f(x,y)\)

функція двох змінних

функція\(z=f(x,y)\), яка відображає кожну впорядковану пару\((x,y)\) в\(D\) підмножині з\(R^2\) унікальним дійсним числом\(z\)

граф функції двох змінних

множина впорядкованих трійок\((x,y,z)\), що задовольняє рівнянню,\(z=f(x,y)\) побудованому в тривимірному декартовому просторі

крива рівня функції двох змінних

множина точок, що задовольняють рівнянню\(f(x,y)=c\) для деякого дійсного числа\(c\) в діапазоні\(f\)

поверхня рівня функції трьох змінних

множина точок, що задовольняють рівнянню\(f(x,y,z)=c\) для деякого дійсного числа\(c\) в діапазоні\(f\)

поверхні

графік функції двох змінних,\(z=f(x,y)\)

вертикальний слід

множина впорядкованих трійок\((c,y,z)\), що вирішує рівняння\(f(c,y)=z\) для заданої константи\(x=c\) або множина впорядкованих трійок\((x,d,z)\), що вирішує рівняння\(f(x,d)=z\) для заданої константи\(y=d\)