16.1: Векторні поля
- Page ID
- 62306
- Розпізнати векторне поле в площині або в просторі.
- Намалюйте векторне поле з заданого рівняння.
- Визначте консервативне поле і пов'язану з нею потенційну функцію.
Векторні поля є важливим інструментом для опису багатьох фізичних понять, таких як гравітація та електромагнетизм, які впливають на поведінку об'єктів над великою областю площини або простору. Вони також корисні для боротьби з масштабною поведінкою, такою як атмосферні бурі або глибоководні океанічні течії. У цьому розділі ми розглядаємо основні визначення та графіки векторних полів, щоб ми могли їх більш детально вивчити в решті цієї глави.
Приклади векторних полів
Як ми можемо змоделювати гравітаційну силу, яку чинять кілька астрономічних об'єктів? Як ми можемо змоделювати швидкість частинок води на поверхні річки? Малюнок\(\PageIndex{1}\) дає візуальні уявлення про такі явища.
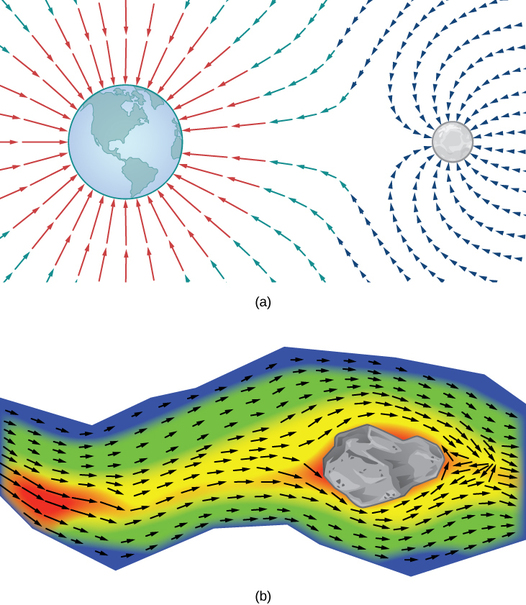
\(\PageIndex{1a}\)На малюнку показано гравітаційне поле, яке чиниться двома астрономічними об'єктами, такими як зірка і планета або планета і місяць. У будь-якій точці малюнка вектор, пов'язаний з точкою, дає чисту гравітаційну силу, що чиниться двома об'єктами на об'єкт одиничної маси. Вектори найбільшої величини на малюнку є векторами, найближчими до більшого об'єкту. Більший об'єкт має більшу масу, тому він надає гравітаційну силу більшої величини, ніж менший об'єкт.
Малюнок\(\PageIndex{1b}\) показує швидкість річки в точках на її поверхні. Вектор, пов'язаний з заданою точкою на поверхні річки, дає швидкість води в цій точці. Так як вектори зліва від фігури невеликі за величиною, вода тече повільно по тій частині поверхні. Коли вода рухається зліва направо, вона стикається з деякими порогами навколо скелі. Швидкість води збільшується, і в частині порогів виникає вир.
Кожен малюнок ілюструє приклад векторного поля. Інтуїтивно векторне поле - це карта векторів. У цьому розділі ми вивчаємо векторні поля в\(ℝ^2\) і\(ℝ^3\).
- Векторне поле\(\vecs{F}\) в\(ℝ^2\) - це присвоєння двовимірного вектора\(\vecs{F}(x,y)\) кожній\((x,y)\) точці\(D\) підмножини\(ℝ^2\). \(D\)Підмножина - область векторного поля.
- Векторне поле\(\vecs{F}\) в\(ℝ^3\) - це присвоєння тривимірного вектора\(\vecs{F}(x,y,z)\) кожній\((x,y,z)\) точці\(D\) підмножини\(ℝ^3\). \(D\)Підмножина - область векторного поля.
Векторні поля в\(ℝ^2\)
Векторне поле в\(ℝ^2\) може бути представлено одним з двох еквівалентних способів. Перший спосіб полягає у використанні вектора з компонентами, які є двозмінними функціями:
\[\vecs{F}(x,y)=⟨P(x,y),Q(x,y)⟩ \nonumber \]
Другий спосіб полягає у використанні стандартних одиничних векторів:
\[\vecs{F}(x,y)=P(x,y) \,\hat{\mathbf i}+Q(x,y) \,\hat{\mathbf j}. \nonumber \]
Векторне поле називається безперервним, якщо його компонентні функції є безперервними.
\(\vecs{F} (x,y)=(2y^2+x−4)\,\hat{\mathbf i}+\cos(x)\,\hat{\mathbf j}\)Дозволяти бути векторним полем в\(ℝ^2\). Зауважте, що це приклад неперервного векторного поля, оскільки обидві компонентні функції є неперервними. Який вектор пов'язаний з точковим\((0,−1)\)?
Рішення
Підставляємо значення точок для\(x\) і\(y\):
\[\begin{align*} \vecs{F} (0,-1) &=(2{(−1)}^2+0−4) \,\hat{\mathbf i}+\cos(0) \,\hat{\mathbf j} \\[4pt] &=−2 \,\hat{\mathbf i} + \hat{\mathbf j}. \end{align*}\]
\(\vecs{G}(x,y)=x^2y\,\hat{\mathbf i}−(x+y)\,\hat{\mathbf j}\)Дозволяти бути векторним полем в\(ℝ^2\). Який вектор пов'язаний з точкою\((−2,3)\)?
- Підказка
-
Підставляємо значення точок у векторну функцію.
- Відповідь
-
\(\vecs{G}(−2,3)=12\hat{\mathbf i}−\hat{\mathbf j}\)
Малювання векторного поля
Тепер ми можемо представляти векторне поле з точки зору його компонентів функцій або одиничних векторів, але представляти його візуально шляхом ескізу є більш складним, оскільки область векторного поля знаходиться в\(ℝ^2\), як і діапазон. Тому «граф» векторного поля\(ℝ^2\) живе в чотиривимірному просторі. Оскільки ми не можемо представляти чотиривимірний простір візуально, ми замість цього малюємо векторні поля\(ℝ^2\) в самій площині. Для цього намалюйте вектор, пов'язаний із заданою точкою в точці площини. Наприклад, припустимо, що вектор, пов'язаний з точкою\((4,−1)\), є\(⟨3,1⟩\). Потім, ми б малювати вектор\(⟨3,1⟩\) в точці\((4,−1)\).
Ми повинні побудувати достатньо векторів, щоб побачити загальну форму, але не стільки, щоб ескіз перетворився на безлад. Якби ми побудували вектор зображення в кожній точці регіону, він би заповнив регіон повністю і марний. Натомість ми можемо вибрати точки на перетині ліній сітки і побудувати зразок з декількох векторів з кожного квадранта прямокутної системи координат в\(ℝ^2\).
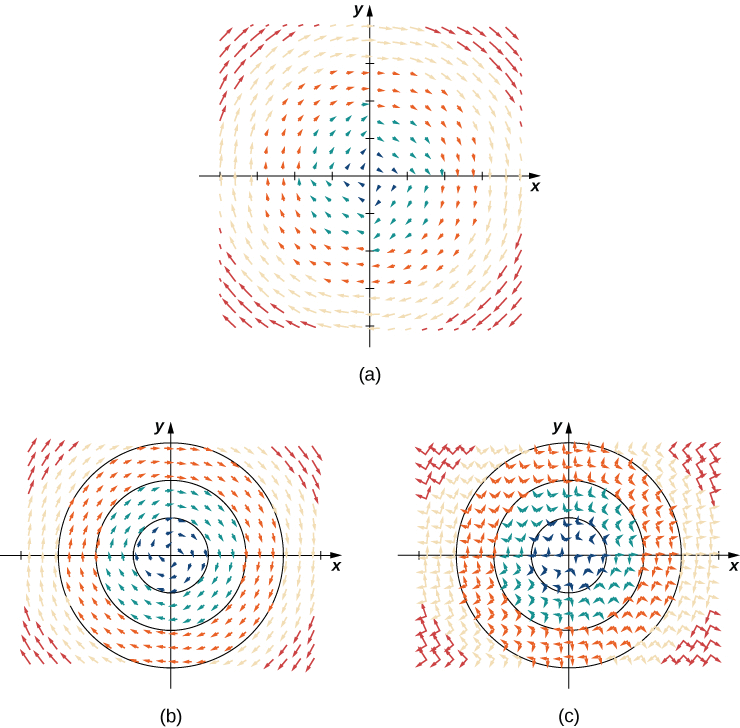
Існує два типи векторних полів,\(ℝ^2\) на яких фокусується ця глава: радіальні поля і поля обертання. Радіальні поля моделюють певні гравітаційні поля та поля джерела енергії, а обертальні поля моделюють рух рідини у вихорі. У радіальному полі всі вектори або спрямовані безпосередньо в бік або безпосередньо від початку. Крім того, величина будь-якого вектора залежить тільки від його відстані від початку. У радіальному полі вектор, розташований в точці\((x,y)\), перпендикулярний окружності з центром у початку, що містить точку\((x,y)\), а всі інші вектори на цьому колі мають однакову величину.
Намалюйте векторне поле\(\vecs{F} (x,y)=\dfrac{x}{2}\hat{\mathbf i}+\dfrac{y}{2}\hat{\mathbf j}\).
Рішення
Щоб намалювати це векторне поле, виберіть зразок точок з кожного квадранта та обчислите відповідний вектор. Наступна таблиця дає репрезентативну вибірку точок на площині і відповідних векторів.
| \((x,y)\) | \(\vecs{F}(x,y)\) | \((x,y)\) | \(\vecs{F}(x,y)\) | \((x,y)\) | \(\vecs{F}(x,y)\) |
|---|---|---|---|---|---|
| \ (x, y)\)» style="вертикальне вирівнювання: середина; ">\((1,0)\) | \ (\ vecs {F} (x, y)\)» style="вертикальне вирівнювання: середина; ">\(⟨\dfrac{1}{2},0⟩\) | \ (x, y)\)» style="вертикальне вирівнювання: середина; ">\((2,0)\) | \ (\ vecs {F} (x, y)\)» style="вертикальне вирівнювання: середина; ">\(⟨1,0⟩\) | \ (x, y)\)» style="вертикальне вирівнювання: середина; ">\((1,1)\) | \ (\ vecs {F} (x, y)\)» style="вертикальне вирівнювання: середина; ">\(⟨\dfrac{1}{2},\dfrac{1}{2}⟩\) |
| \ (x, y)\)» style="вертикальне вирівнювання: середина; ">\((0,1)\) | \ (\ vecs {F} (x, y)\)» style="вертикальне вирівнювання: середина; ">\(⟨0,\dfrac{1}{2}⟩\) | \ (x, y)\)» style="вертикальне вирівнювання: середина; ">\((0,2)\) | \ (\ vecs {F} (x, y)\)» style="вертикальне вирівнювання: середина; ">\(⟨0,1⟩\) | \ (x, y)\)» style="вертикальне вирівнювання: середина; ">\((−1,1)\) | \ (\ vecs {F} (x, y)\)» style="вертикальне вирівнювання: середина; ">\(⟨−\dfrac{1}{2},\dfrac{1}{2}⟩\) |
| \ (x, y)\)» style="вертикальне вирівнювання: середина; ">\((−1,0)\) | \ (\ vecs {F} (x, y)\)» style="вертикальне вирівнювання: середина; ">\(⟨−\dfrac{1}{2},0⟩\) | \ (x, y)\)» style="вертикальне вирівнювання: середина; ">\((−2,0)\) | \ (\ vecs {F} (x, y)\)» style="вертикальне вирівнювання: середина; ">\(⟨−1,0⟩\) | \ (x, y)\)» style="вертикальне вирівнювання: середина; ">\((−1,−1)\) | \ (\ vecs {F} (x, y)\)» style="вертикальне вирівнювання: середина; ">\(⟨−\dfrac{1}{2},−\dfrac{1}{2}⟩\) |
| \ (x, y)\)» style="вертикальне вирівнювання: середина; ">\((0,−1)\) | \ (\ vecs {F} (x, y)\)» style="вертикальне вирівнювання: середина; ">\(⟨0,−\dfrac{1}{2}⟩\) | \ (x, y)\)» style="вертикальне вирівнювання: середина; ">\((0,−2)\) | \ (\ vecs {F} (x, y)\)» style="вертикальне вирівнювання: середина; ">\(⟨0,−1⟩\) | \ (x, y)\)» style="вертикальне вирівнювання: середина; ">\((1,−1)\) | \ (\ vecs {F} (x, y)\)» style="вертикальне вирівнювання: середина; ">\(⟨\dfrac{1}{2},−\dfrac{1}{2}⟩\) |
На малюнку\(\PageIndex{2a}\) показано векторне поле. Щоб побачити, що кожен вектор перпендикулярний відповідному колу, на малюнку\(\PageIndex{2b}\) показані кола, накладені на векторне поле.
Намалюйте радіальне поле\(\vecs{F} (x,y)=−\dfrac{x}{3}\hat{\mathbf i}−\dfrac{y}{3}\hat{\mathbf j}\).
- Підказка
-
Намалюйте достатньо векторів, щоб отримати уявлення про фігуру.
- Відповідь
-

На відміну від радіальних полів, в обертальному полі вектор в точці\((x,y)\) є дотичним (не перпендикулярним) до кола з радіусом\(r=\sqrt{x^2+y^2}\). У стандартному обертальному полі всі вектори вказують або за годинниковою стрілкою, або в напрямку проти годинникової стрілки, а величина вектора залежить тільки від його відстані від початку. Обидва наступні приклади є обертальними полями за годинниковою стрілкою, і ми бачимо з їх візуальних уявлень, що вектори, здається, обертаються навколо початку.
Намалюйте векторне поле\(\vecs{F} (x,y)=⟨y,\,−x⟩\).
Рішення
Створіть таблицю (див. наступну), використовуючи репрезентативну вибірку точок на площині та відповідних їм векторів. \(\PageIndex{3}\)На малюнку показано результуюче векторне поле.
| \((x,y)\) | \(\vecs{F}(x,y)\) | \((x,y)\) | \(\vecs{F}(x,y)\) | \((x,y)\) | \(\vecs{F}(x,y)\) |
|---|---|---|---|---|---|
| \ (x, y)\)» style="вертикальне вирівнювання: середина; ">\((1,0)\) | \ (\ vecs {F} (x, y)\)» style="вертикальне вирівнювання: середина; ">\(⟨0,−1⟩\) | \ (x, y)\)» style="вертикальне вирівнювання: середина; ">\((2,0)\) | \ (\ vecs {F} (x, y)\)» style="вертикальне вирівнювання: середина; ">\(⟨0,−2⟩\) | \ (x, y)\)» style="вертикальне вирівнювання: середина; ">\((1,1)\) | \ (\ vecs {F} (x, y)\)» style="вертикальне вирівнювання: середина; ">\(⟨1,−1⟩\) |
| \ (x, y)\)» style="вертикальне вирівнювання: середина; ">\((0,1)\) | \ (\ vecs {F} (x, y)\)» style="вертикальне вирівнювання: середина; ">\(⟨1,0⟩\) | \ (x, y)\)» style="вертикальне вирівнювання: середина; ">\((0,2)\) | \ (\ vecs {F} (x, y)\)» style="вертикальне вирівнювання: середина; ">\(⟨2,0⟩\) | \ (x, y)\)» style="вертикальне вирівнювання: середина; ">\((−1,1)\) | \ (\ vecs {F} (x, y)\)» style="вертикальне вирівнювання: середина; ">\(⟨1,1⟩\) |
| \ (x, y)\)» style="вертикальне вирівнювання: середина; ">\((−1,0)\) | \ (\ vecs {F} (x, y)\)» style="вертикальне вирівнювання: середина; ">\(⟨0,1⟩\) | \ (x, y)\)» style="вертикальне вирівнювання: середина; ">\((−2,0)\) | \ (\ vecs {F} (x, y)\)» style="вертикальне вирівнювання: середина; ">\(⟨0,2⟩\) | \ (x, y)\)» style="вертикальне вирівнювання: середина; ">\((−1,−1)\) | \ (\ vecs {F} (x, y)\)» style="вертикальне вирівнювання: середина; ">\(⟨−1,1⟩\) |
| \ (x, y)\)» style="вертикальне вирівнювання: середина; ">\((0,−1)\) | \ (\ vecs {F} (x, y)\)» style="вертикальне вирівнювання: середина; ">\(⟨−1,0⟩\) | \ (x, y)\)» style="вертикальне вирівнювання: середина; ">\((0,−2)\) | \ (\ vecs {F} (x, y)\)» style="вертикальне вирівнювання: середина; ">\(⟨−2,0⟩\) | \ (x, y)\)» style="вертикальне вирівнювання: середина; ">\((1,−1)\) | \ (\ vecs {F} (x, y)\)» style="вертикальне вирівнювання: середина; ">\(⟨−1,−1⟩\) |
Аналіз
Зверніть увагу, що вектор\(\vecs{F}(a,b)=⟨b,−a⟩\) вказує за годинниковою стрілкою і перпендикулярний\(⟨a,b⟩\) радіальному (Ми можемо перевірити це твердження, обчисливши точковий добуток двох векторів:\(⟨a,b⟩·⟨−b,a⟩=−ab+ab=0\).) Крім того, вектор\(⟨b,−a⟩\) має довжину\(r=\sqrt{a^2+b^2}\). Таким чином, ми маємо повний опис цього обертального векторного поля: вектор, пов'язаний з точкою,\((a,b)\) є вектором довжиною r дотичною до кола радіусом r, і він вказує в напрямку за годинниковою стрілкою.
Ескізи, такі як на малюнку, часто\(\PageIndex{3}\) використовуються для аналізу основних штормових систем, включаючи урагани та циклони. У північній півкулі шторми обертаються проти годинникової стрілки; в південній півкулі шторми обертаються за годинниковою (Це ефект, спричинений обертанням Землі навколо своєї осі і називається ефектом Коріоліса.)

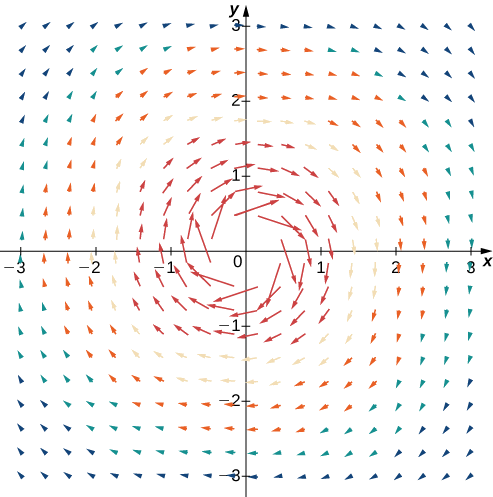
Ескіз векторного поля\(\vecs{F}(x,y)=\dfrac{y}{x^2+y^2}\hat{\mathbf i}, -\dfrac{x}{x^2+y^2}\hat{\mathbf j}\).
Рішення
Щоб візуалізувати це векторне поле, спочатку зауважте, що точковий\(\vecs{F}(a,b)·(a \,\hat{\mathbf i}+b \,\hat{\mathbf j})\) добуток дорівнює нулю для будь-якої точки\((a,b)\). Тому кожен вектор дотичний до кола, на якому він розташований. Також, як\((a,b)\rightarrow(0,0)\), величина\(\vecs{F}(a,b)\) йде в нескінченність. Щоб переконатися в цьому, зверніть увагу, що
\(||\vecs{F}(a,b)||=\sqrt{\dfrac{a^2+b^2}{ {(a^2+b^2)}^2 }} =\sqrt{\dfrac{1}{a^2+b^2}}\).
Так\(\dfrac{1}{a^2+b^2}\rightarrow \infty\) як як\((a,b)\rightarrow (0,0)\), то\(||\vecs F(a,b)||\rightarrow \infty\) як\((a,b)\rightarrow (0,0)\). Це векторне поле виглядає аналогічно векторному полю в прикладі\(\PageIndex{3}\), але в цьому випадку величини векторів, близьких до початку, великі. Таблиця\(\PageIndex{3}\) показує вибірку точок і відповідні вектори, а на малюнку\(\PageIndex{5}\) показано векторне поле. Зауважимо, що це векторне поле моделює вир руху річки на малюнку\(\PageIndex{5}\) (б). Домен цього векторного поля є все,\(ℝ^2\) крім точки\((0,0)\).
| \((x,y)\) | \(\vecs{F}(x,y)\) | \((x,y)\) | \(\vecs{F}(x,y)\) | \((x,y)\) | \(\vecs{F}(x,y)\) |
|---|---|---|---|---|---|
| \ (x, y)\)» style="вертикальне вирівнювання: середина; ">\((1,0)\) | \ (\ vecs {F} (x, y)\)» style="вертикальне вирівнювання: середина; ">\(⟨0,−1⟩\) | \ (x, y)\)» style="вертикальне вирівнювання: середина; ">\((2,0)\) | \ (\ vecs {F} (x, y)\)» style="вертикальне вирівнювання: середина; ">\(⟨0,−\dfrac{1}{2}⟩\) | \ (x, y)\)» style="вертикальне вирівнювання: середина; ">\((1,1)\) | \ (\ vecs {F} (x, y)\)» style="вертикальне вирівнювання: середина; ">\(⟨\dfrac{1}{2},−\dfrac{1}{2}⟩\) |
| \ (x, y)\)» style="вертикальне вирівнювання: середина; ">\((0,1)\) | \ (\ vecs {F} (x, y)\)» style="вертикальне вирівнювання: середина; ">\(⟨1,0⟩\) | \ (x, y)\)» style="вертикальне вирівнювання: середина; ">\((0,2)\) | \ (\ vecs {F} (x, y)\)» style="вертикальне вирівнювання: середина; ">\(⟨\dfrac{1}{2},0⟩\) | \ (x, y)\)» style="вертикальне вирівнювання: середина; ">\((−1,1)\) | \ (\ vecs {F} (x, y)\)» style="вертикальне вирівнювання: середина; ">\(⟨\dfrac{1}{2},\dfrac{1}{2}⟩\) |
| \ (x, y)\)» style="вертикальне вирівнювання: середина; ">\((−1,0)\) | \ (\ vecs {F} (x, y)\)» style="вертикальне вирівнювання: середина; ">\(⟨0,1⟩\) | \ (x, y)\)» style="вертикальне вирівнювання: середина; ">\((−2,0)\) | \ (\ vecs {F} (x, y)\)» style="вертикальне вирівнювання: середина; ">\(⟨0,\dfrac{1}{2}⟩\) | \ (x, y)\)» style="вертикальне вирівнювання: середина; ">\((−1,−1)\) | \ (\ vecs {F} (x, y)\)» style="вертикальне вирівнювання: середина; ">\(⟨−\dfrac{1}{2},\dfrac{1}{2}⟩\) |
| \ (x, y)\)» style="вертикальне вирівнювання: середина; ">\((0,−1)\) | \ (\ vecs {F} (x, y)\)» style="вертикальне вирівнювання: середина; ">\(⟨−1,0⟩\) | \ (x, y)\)» style="вертикальне вирівнювання: середина; ">\((0,−2)\) | \ (\ vecs {F} (x, y)\)» style="вертикальне вирівнювання: середина; ">\(⟨−\dfrac{1}{2},0⟩\) | \ (x, y)\)» style="вертикальне вирівнювання: середина; ">\((1,−1)\) | \ (\ vecs {F} (x, y)\)» style="вертикальне вирівнювання: середина; ">\(⟨−\dfrac{1}{2},−\dfrac{1}{2}⟩\) |
Ескіз векторного поля\(\vecs{F}(x,y)=⟨−2y,\,2x⟩\). Векторне поле радіальне, обертальне чи ні?
- Підказка
-
Підставляйте достатньо очок,\(\vecs{F}\) щоб отримати уявлення про форму.
- Відповідь
-
обертальний

\(\vecs{v} (x,y)=−\dfrac{2y}{x^2+y^2}\hat{\mathbf i}+\dfrac{2x}{x^2+y^2}\hat{\mathbf j}\)Припустимо, що це поле швидкості рідини. Як швидко рухається рідина в точці\((1,−1)\)? (Припустимо, одиниці швидкості - метри в секунду.)
Рішення
Щоб знайти швидкість рідини в точці\((1,−1)\), підставляємо точку на\(\vecs{v} \):
\(\vecs{v}(1,−1)=\dfrac{−2(−1)}{1+1}\hat{\mathbf i}+\dfrac{2(1)}{1+1}\hat{\mathbf j}=\hat{\mathbf i}+\hat{\mathbf j}\).
Швидкість руху рідини при\((1,−1)\) - це величина цього вектора. Тому швидкість дорівнює\(||\hat{\mathbf i}+\hat{\mathbf j}||=\sqrt{2}\) м/сек.
Векторне поле\(\vecs{v} (x,y)=⟨4|x|,\,1⟩\) моделює швидкість води на поверхні річки. Яка швидкість води в точці\((2,3)\)? Використовуйте метри в секунду як одиниці виміру.
- Підказка
-
Пам'ятайте, швидкість - це величина швидкості.
- Відповідь
-
\(\sqrt{65}\)м/сек
Ми розглянули векторні поля, які містять вектори різної величини, але так само, як у нас є одиничні вектори, ми також можемо мати одиничне векторне поле. \(\vecs{F}\)Векторне поле - це одиничне векторне поле, якщо величина кожного вектора в полі дорівнює 1. У полі одиничного вектора єдиною релевантною інформацією є напрямок кожного вектора.
Показати, що\(\vecs{F} (x,y)=\left\langle\dfrac{y}{\sqrt{x^2+y^2}},−\dfrac{x}{\sqrt{x^2+y^2}}\right\rangle\) векторне поле є одиничним векторним полем.
Рішення
Щоб показати, що\(\vecs{F}\) це одиничне поле, ми повинні показати, що величина кожного вектора є\(1\). Зауважте, що
\[\begin{align*} \sqrt{ \left(\dfrac{y}{\sqrt{x^2+y^2}}\right)^2+\left(−\dfrac{x}{\sqrt{x^2+y^2}}\right)^2} &=\sqrt{ \dfrac{y^2}{x^2+y^2}+\dfrac{x^2}{x^2+y^2}} \\[4pt] &=\sqrt{\dfrac{x^2+y^2}{x^2+y^2}} \\[4pt] &=1 \end{align*}\]
Тому\(\vecs{F} \) є одиничним векторним полем.
Векторне поле є\(\vecs{F} (x,y)=⟨−y,\,x⟩\) одиничним векторним полем?
- Підказка
-
Обчисліть величину\(\vecs{F} \) в довільній точці\((x,y)\).
- Відповідь
-
Ні.
Чому поля векторних одиниць важливі? Припустимо, ми вивчаємо потік рідини, і піклуємося тільки про те, в якому напрямку тече рідина в даній точці. При цьому швидкість рідини (яка є величиною відповідного вектора швидкості) не має значення, тому що все, про що нас хвилює, - це напрямок кожного вектора. Тому поле одиничного вектора, пов'язане зі швидкістю, - це поле, яке ми б вивчали.
Якщо\(\vecs{F} =⟨P,Q,R⟩\) є векторним полем, то відповідне поле вектора одиниці є\(\big\langle\tfrac{P}{||\vecs F||},\tfrac{Q}{||\vecs F||},\tfrac{R}{||\vecs F||}\big\rangle\). Зверніть увагу, що якщо\(\vecs{F}(x,y)=⟨y,\,−x⟩\) є векторним полем з Прикладу\(\PageIndex{6}\), то величина\(\vecs{F} \) є\(\sqrt{x^2+y^2}\), і тому відповідне поле вектора одиниці є полем\(\vecs{G} \) з попереднього прикладу.
Якщо\(\vecs{F} \) є векторним полем, то процес ділення\(\vecs{F} \) на його величину з утворенням одиничного векторного поля\(\vecs{F}/||\vecs{F}||\) називається нормалізацією поля\(\vecs{F} \).
Векторні поля в\(ℝ^3\)
Ми бачили кілька прикладів векторних полів в\(ℝ^2\); давайте тепер звернемо нашу увагу на векторні поля в\(ℝ^3\). Ці векторні поля можуть бути використані для моделювання гравітаційних або електромагнітних полів, а також вони можуть бути використані для моделювання потоку рідини або теплового потоку в трьох вимірах. Двовимірне векторне поле дійсно може моделювати лише рух води на двовимірному фрагменті річки (наприклад, поверхні річки). Оскільки річка протікає через три просторові виміри, для моделювання течії всієї глибини річки нам потрібно векторне поле в трьох вимірах.
Додатковий вимір тривимірного поля може зробити векторні поля\(ℝ^3\) більш важкими для візуалізації, але ідея така ж. Щоб візуалізувати векторне поле в\(ℝ^3\), намалюйте достатньо векторів, щоб показати загальну форму. Ми можемо використовувати подібний метод для візуалізації векторного поля,\(ℝ^2\) вибираючи точки в кожному октанті.
Так само, як і з векторними полями в\(ℝ^2\), ми можемо представляти векторні поля в\(ℝ^3\) з компонентними функціями. Нам просто потрібна додаткова функція компонента для додаткового виміру. Пишемо або
\[\vecs{F}(x,y,z)=⟨P(x,y,z),Q(x,y,z),R(x,y,z)⟩ \nonumber \]
або
\[\vecs{F}(x,y,z)=P(x,y,z)\hat{\mathbf i}+Q(x,y,z)\hat{\mathbf j}+R(x,y,z)\hat{\mathbf k}. \nonumber \]
Опишіть векторне поле\(\vecs{F}(x,y,z)=⟨1,\,1,\,z⟩\).
Рішення
Для цього векторного поля\(x\) - і\(y\) -компоненти є постійними, тому кожна точка\(ℝ^3\) має пов'язаний вектор з\(x\) - і\(y\) -компонентами, рівними одиниці. Для візуалізації спочатку розглянемо\(\vecs{F}\), як виглядає поле в\(xy\) -площині. У\(xy\) -площині,\(z=0\). Значить, кожна точка форми\((a,b,0)\) має вектор,\(⟨1,1,0⟩\) пов'язаний з нею. Для точок не в\(xy\) -площині, а трохи вище неї, пов'язаний вектор має невеликий, але позитивний\(z\) -компонент, і тому пов'язаний вектор вказує трохи вгору. Для точок, які знаходяться набагато вище\(xy\) -площини,\(z\) -компонент великий, тому вектор майже вертикальний. На малюнку\(\PageIndex{6}\) показано це векторне поле.
Малюнок\(\PageIndex{6}\): Візуальне зображення векторного поля\(\vecs{F}(x,y,z)=⟨1,1,z⟩\).
Ескіз векторного поля\(\vecs{G}(x,y,z)=⟨2,\,\dfrac{z}{2},\,1⟩\).
- Підказка
-
Підставте достатню кількість точок у векторне поле, щоб отримати уявлення про загальну форму.
- Відповідь
У наступному прикладі ми досліджуємо один з класичних випадків тривимірного векторного поля: гравітаційне поле.
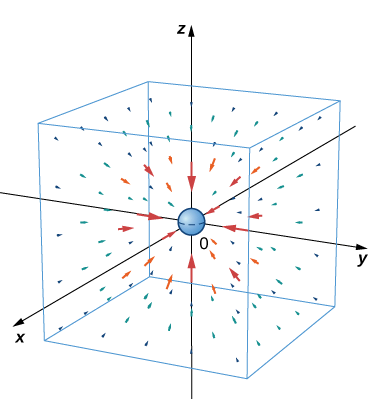
Закон гравітації Ньютона стверджує\(\vecs{F}=−G\dfrac{m_1m_2}{r^2}\hat{\mathbf r}\), що, де G - універсальна гравітаційна константа. Він описує гравітаційне поле, що чиниться об'єктом (об'єктом 1) маси,\(m_1\) розташованим біля початку на іншому об'єкті (об'єкті 2) маси,\(m_2\) розташованому в точці\((x,y,z)\). Поле\(\vecs{F}\) позначає гравітаційну силу, яку об'єкт 1 чинить на об'єкт 2,\(r\) - це відстань між двома об'єктами, і\(\hat{\mathbf r}\) вказує одиничний вектор від першого об'єкта до другого. Знак мінус показує, що гравітаційна сила притягує до початку; тобто сила предмета 1 приваблива. Намалюйте векторне поле, пов'язане з цим рівнянням.
Рішення
Так як об'єкт 1 розташований біля початку, відстань між об'єктами задається\(r=\sqrt{x^2+y^2+z^2}\). Одиничний вектор від об'єкта 1 до об'єкта 2 є\(\hat{\mathbf r}=\dfrac{⟨x,y,z⟩}{||⟨x,y,z⟩||}\), а значить\(\hat{\mathbf r}=\big\langle\dfrac{x}{r},\dfrac{y}{r},\dfrac{z}{r}\big\rangle\). Отже, гравітаційне векторне поле,\(\vecs{F}\) що діє об'єктом 1 на об'єкт 2, дорівнює
\[ \vecs{F}=−Gm_1m_2\big\langle\dfrac{x}{r^3},\dfrac{y}{r^3},\dfrac{z}{r^3}\big\rangle. \nonumber \]
Це приклад радіального векторного поля в\(ℝ^3\).
\(\PageIndex{7}\)На малюнку показано, як виглядає це гравітаційне поле для великої маси біля початку. Зауважте, що величини векторів збільшуються у міру наближення векторів до початку.
Маса астероїда 1 становить 750 000 кг, а маса астероїда 2 - 130 000 кг. Припустимо, що астероїд 1 розташований біля початку, а астероїд 2 розташований на\((15,−5,10)\), вимірюється в одиницях від 10 до восьмої потужності кілометрів. Враховуючи, що універсальна гравітаційна константа є\(G=6.67384×10^{−11}m^3{kg}^{−1}s^{−2}\), знайдіть вектор гравітаційної сили, який астероїд 1 надає на астероїд 2.
- Підказка
-
Дотримуйтесь Приклад\(\PageIndex{8}\) і спочатку обчислите відстань між астероїдами.
- Відповідь
-
\(1.49063×{10}^{−18}\),\(4.96876×{10}^{−19}\),\(9.93752×{10}^{−19}\) Н
Градієнтні поля (консервативні поля)
У цьому розділі ми вивчаємо особливий вид векторного поля, який називається градієнтним полем або консервативним полем. Ці векторні поля надзвичайно важливі у фізиці, оскільки вони можуть бути використані для моделювання фізичних систем, в яких зберігається енергія. Гравітаційні поля та електричні поля, пов'язані зі статичним зарядом, є прикладами градієнтних полів.
Нагадаємо, що якщо\(f\) є (скалярною) функцією\(x\) і\(y\), то градієнт\(f\) є
\[ \text{grad}\, f =\vecs \nabla f(x,y) =f_x(x,y) \hat{\mathbf i} +f_y(x,y) \hat{\mathbf j}. \nonumber \]
Ми можемо бачити з форми, в якій градієнт написано, що\(\vecs \nabla f\) є векторним полем в\(ℝ^2\). Аналогічно, якщо\(f\) є функцією\(x\)\(y\), і\(z\), то\(f\) градієнт
\[ \text{grad}\, f =\vecs \nabla f(x,y,z) = f_x(x,y,z) \hat{\mathbf i}+f_y(x,y,z) \hat{\mathbf j}+f_z(x,y,z)\hat{\mathbf k}. \nonumber \]
Градієнт тризмінної функції є векторним полем в\(ℝ^3\). Градієнтне поле - це векторне поле, яке можна записати як градієнт функції, і ми маємо наступне визначення.
Векторне поле\(\vecs{F}\) в\(ℝ^2\) або в\(ℝ^3\) є градієнтним полем, якщо існує скалярна функція\(f\) така, що\(\vecs \nabla f=\vecs{F}\).
Використовуйте технологію для побудови векторного поля градієнта\(f(x,y)=x^2y^2\).
Рішення
Градієнт\(f\) є\(\vecs \nabla f(x,y)=⟨2xy^2,\,2x^2y⟩\). Для ескізу векторного поля використовуйте систему комп'ютерної алгебри, таку як Mathematica. Малюнок\(\PageIndex{8}\) показує\(\vecs \nabla f\).
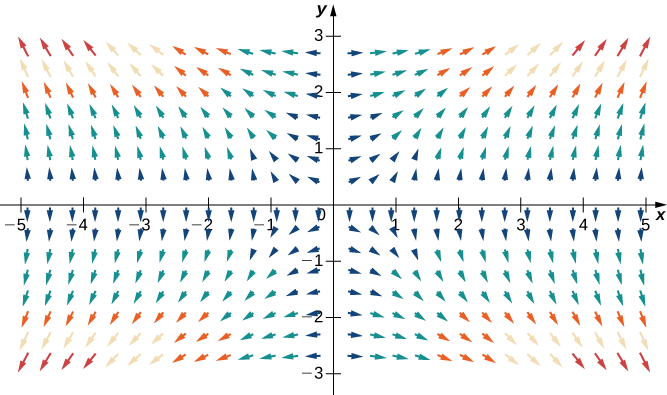
Використовуйте технологію для побудови векторного поля градієнта\(f(x,y)=\sin x\cos y\).
- Підказка
-
Знайдіть градієнт\(f\).
- Відповідь
-
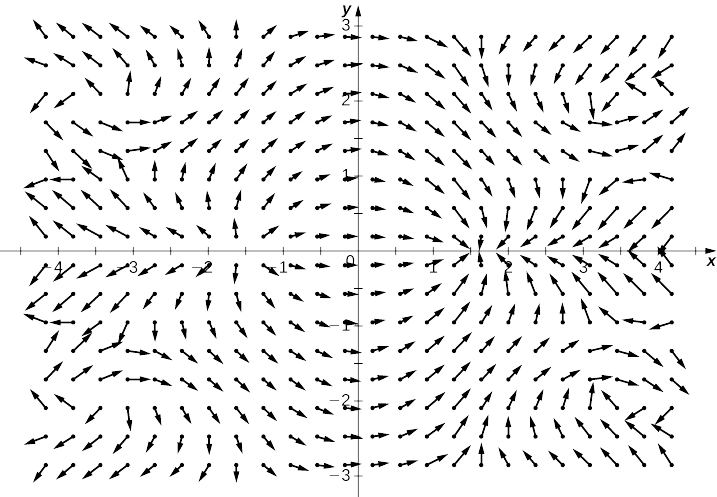
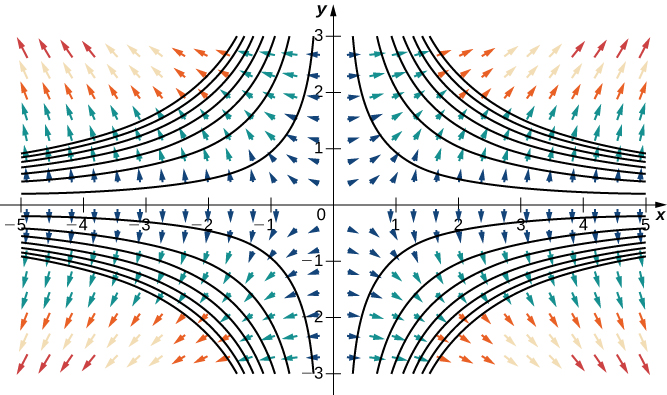
Розглянемо функцію\(f(x,y)=x^2y^2\) з Прикладу\(\PageIndex{9}\). \(\PageIndex{9}\)На малюнку показані криві рівня цієї функції, накладені на векторне поле градієнта функції. Вектори градієнта перпендикулярні кривим рівня, і величини векторів стають більшими, коли криві рівня зближуються, оскільки тісно згруповані криві рівня вказують на те, що графік крутий, а величина вектора градієнта є найбільшим значенням спрямованої похідної. Таким чином, ви можете побачити локальну крутизну графа, досліджуючи градієнтне поле відповідної функції.
Як ми дізналися раніше,\(\vecs{F}\) векторне поле - це консервативне векторне поле, або градієнтне поле, якщо існує скалярна функція\(f\) така, що\(\vecs \nabla f=\vecs{F}\). У цій ситуації\(f\) називається потенційна функція для\(\vecs{F}\). Консервативні векторні поля виникають у багатьох додатках, особливо у фізиці. Причина, по якій такі поля називаються консервативними, полягає в тому, що вони моделюють сили фізичних систем, в яких зберігається енергія. Більш детально ми вивчаємо консервативні векторні поля далі в цьому розділі.
Ви можете помітити, що в деяких додатках потенційна функція\(f\) для\(\vecs{F}\) визначається замість такої функції, що\(−\vecs \nabla f=\vecs{F}\). Це стосується певних контекстів у фізиці, наприклад.
Є\(f(x,y,z)=x^2yz−\sin(xy)\) потенційною функцією для векторного поля
\(\vecs{F}(x,y,z)=⟨2xyz−y\cos(xy),x^2z−x\cos(xy),x^2y⟩\)?
Рішення
Нам потрібно підтвердити, чи є\(\vecs \nabla f=\vecs{F}\). У нас є
\[ \begin{align*} f_x(x,y) =2xyz−y\cos(xy) \\[4pt] f_y(x,y) =x^2z−x\cos(xy) \\[4pt] f_z(x,y) =x^2y \end{align*}. \nonumber \]
Тому\(\vecs \nabla f=\vecs{F}\) і\(f\) є потенційною функцією для\(\vecs{F}\).
Чи\(f(x,y,z)=x^2\cos(yz)+y^2z^2\) є потенційна функція для\(\vecs{F}(x,y,z)=⟨2x\cos(yz),−x^2z \sin(yz)+2yz^2,y^2⟩\)?
- Підказка
-
Обчислити градієнт\(f\).
- Відповідь
-
Ні
Швидкість рідини моделюється полем\(\vecs v(x,y)=⟨xy,\tfrac{x^2}{2}−y⟩\). Переконайтеся, що\(f(x,y)=\dfrac{x^2y}{2}−\dfrac{y^2}{2}\) це потенційна функція для\(\vecs{v}\).
Рішення
Щоб показати, що\(f\) це потенційна функція, ми повинні показати це\(\vecs \nabla f=\vecs v\). Зверніть увагу, що\(f_x(x,y)=xy\) і\(f_y(x,y)=\dfrac{x^2}{2}−y\). Тому\(\vecs \nabla f(x,y)=⟨xy,\tfrac{x^2}{2}−y⟩\) і\(f\) є потенційною функцією для\(\vecs{v}\) (рис.\(\PageIndex{10}\)).

Переконайтеся, що\(f(x,y)=x^3y^2+x\) це потенційна функція для поля швидкості\(\vecs{v}(x,y)=⟨3x^2y^2+1,2x^3y⟩\).
- Підказка
-
Обчисліть градієнт.
- Відповідь
-
\(\vecs \nabla f(x,y)=\vecs{v}(x,y)\)
Якщо\(\vecs{F}\) є консервативним векторним полем, то існує хоча б одна потенційна функція\(f\) така, що\(\vecs \nabla f=\vecs{F}\). Але чи може бути більше однієї потенційної функції? Якщо так, то чи існує зв'язок між двома потенційними функціями для одного і того ж векторного поля? Перш ніж відповісти на ці питання, давайте згадаємо деякі факти з однозмінного числення, щоб керувати нашою інтуїцією. Нагадаємо, що якщо\(k(x)\) інтегрується функція, то\(k\) має нескінченно багато антипохідних. Крім того, якщо\(\vecs{F}\) і\(\vecs{G}\) є обидва антипохідні\(k\), то\(\vecs{F}\) і\(\vecs{G}\) відрізняються тільки постійною. Тобто є якась кількість\(C\) таких, що\(\vecs{F}(x)=\vecs{G}(x)+C\).
Тепер давайте\(\vecs{F}\) консервативне векторне поле і нехай\(f\) і\(g\) бути потенційними функціями для\(\vecs{F}\). Оскільки градієнт схожий на похідну,\(\vecs{F}\) консервативний означає, що «\(\vecs{F}\)інтегрується» з «антипохідними»\(f\) і\(g\). Тому, якщо аналогія з однозмінним численням справедлива, ми очікуємо, що є якась постійна\(C\) така, що\(f(x)=g(x)+C\). Наступна теорема говорить, що це дійсно так.
Щоб з точністю викласти наступну теорему, потрібно припустити, що область векторного поля пов'язана і відкрита. Підключитися означає, що якщо\(P_1\) і\(P_2\) є будь-якими двома точками в домені, то ви можете йти від\(P_1\) до\(P_2\) уздовж шляху, який залишається повністю всередині домену.
\(\vecs{F}\)Дозволяти консервативне векторне поле на відкритій і пов'язаної області і нехай\(f\) і\(g\) бути функції такі, що\(\vecs \nabla f=\vecs{F}\) і\(\vecs \nabla g=\vecs{F}\). Тоді, є постійна\(C\) така, що\(f=g+C\).
Оскільки\(f\) і\(g\) є обома потенційними функціями для\(\vecs{F}\), то\(\vecs \nabla (f−g)=\vecs \nabla f−\vecs \nabla g=\vecs{F}−\vecs{F}=\vecs 0\). Нехай\(h=f−g\), тоді у нас\(\vecs \nabla h=\vecs 0\) є.Ми хотіли б показати, що\(h\) є постійною функцією.
Припустимо,\(h\) є функцією\(x\) і\(y\) (логіка цього доказу поширюється на будь-яку кількість незалежних змінних). З тих пір\(\vecs \nabla h=\vecs 0\), у нас\(h_x(x,y)=0\) і\(h_y(x,y)=0\). Вираз\(h_x(x,y)=0\) означає, що\(h\) це постійна функція стосовно\(x\) —тобто\(h(x,y)=k_1(y)\) для якоїсь функції\(k_1\). Аналогічно,\(h_y(x,y)=0\) мається\(h(x,y)=k_2(x)\) на увазі для якоїсь функції\(k_2\). Тому функція\(h\) залежить тільки від,\(y\) а також залежить тільки від\(x\). Таким чином,\(h(x,y)=C\) для деякої константи\(C\) на підключеному домені\(\vecs{F}\). Зверніть увагу, що ми дійсно потрібно зв'язність в цей момент; якщо домен\(\vecs{F}\) прийшов у двох окремих частин, то\(k\) може бути постійною\(C_1\) на одній частині, але може бути різною константою\(C_2\) на інший шматок. Так як\(f−g=h=C\), ми маємо це\(f=g+C\), за бажанням.
\(\square\)
Консервативні векторні поля також мають спеціальну властивість, яка називається перехресним частковим властивістю. Ця властивість допомагає перевірити, чи є задане векторне поле консервативним.
\(\vecs{F}\)Дозволяти векторне поле в двох або трьох вимірах таким чином, що компонентні функції\(\vecs{F}\) мають неперервні змішано-частинні похідні другого порядку на області\(\vecs{F}\).
Якщо\(\vecs{F}(x,y)=⟨P(x,y),Q(x,y)⟩\) є консервативним векторним полем в\(ℝ^2\), то
\[\dfrac{\partial P}{\partial y}=\dfrac{\partial Q}{\partial x}. \nonumber \]
Якщо\(\vecs{F}(x,y,z)=⟨P(x,y,z),Q(x,y,z),R(x,y,z)⟩\) є консервативним векторним полем в\({\mathbb{R}}^3\), то
\[ \begin{align*} \dfrac{\partial P}{\partial y} =\dfrac{\partial Q}{\partial x} \\[4pt] \dfrac{\partial Q}{\partial z} =\dfrac{\partial R}{\partial y} \\[4pt] \dfrac{\partial R}{\partial x} =\dfrac{\partial P}{\partial z}. \end{align*}\]
Так\(\vecs{F}\) як консервативний, є функція\(f(x,y)\) така, що\(\vecs \nabla f=\vecs{F}\). Тому за визначенням градієнта,\(f_x=P\) і\(f_y=Q\). За теоремою Клеро\(f_{xy}=f_{yx}\), Але,\(f_{xy}=P_y\) і\(f_{yx}=Q_{x}\), і таким чином\(P_y=Q_x\).
\(\square\)
Теорема Клеро дає швидкий доказ перехресної часткової властивості консервативних векторних полів у\(ℝ^3\), так само, як це було для векторних полів в\(ℝ^2\).
Перехресна часткова властивість консервативних векторних полів показує, що більшість векторних полів не є консервативними. Перехресна часткова властивість загалом важко задовольнити, тому більшість векторних полів не матимуть рівних перехресних частинок.
Показати, що обертальне векторне поле не\(\vecs{F}(x,y)=⟨y,\,−x⟩\) є консервативним.
Рішення
Нехай\(P(x,y)=y\) і\(Q(x,y)=−x\). Якщо\(\vecs{F}\) консервативний, то перехресні були б рівними—тобто\(P_y\) дорівнювали б.\(Q_x\) Тому, щоб показати, що не консервативно, перевірте \(\vecs{F}\)це\(P_y≠Q_x\). Так як\(P_y=1\) і\(Q_x=−1\), векторне поле не консервативне.
Показати, що векторне поле не\(\vecs F(x,y)=xy\,\hat{\mathbf i}−x^2y\,\hat{\mathbf j}\) є консервативним.
- Підказка
-
Перевіряємо поперечні частки.
- Відповідь
-
\(P_y(x,y)=x\)і\(Q_x(x,y)=−2xy\). Так як\(P_y(x,y) ≠ Q_x(x,y)\), не\(\vecs F\) є консервативним.
Чи є векторне поле\(\vecs{F}(x,y,z)=⟨7,−2,x^3⟩\) консервативним?
Рішення
Нехай\(P(x,y,z)=7\),\(Q(x,y,z)=−2\), і\(R(x,y,z)=x^3\). Якщо\(\vecs{F}\) консервативний, то всі три перехресні частинні рівняння будуть задоволені -\(\vecs{F}\) тобто якщо консервативні, то\(P_y\) дорівнювали б\(Q_x\),\(Q_z\) дорівнювали б і\(R_y\)\(R_x\) дорівнювали б\(P_z\). Зауважте, що
\[P_y=Q_x=R_y=Q_z=0 \nonumber \]
тому перші дві необхідні рівності тримаються. Втім,\(R_x(x,y,z)=x^3\) і\(P_z(x,y,z)=0\) так\(R_x≠P_z\). Тому не\(\vecs{F}\) є консервативним.
Чи є векторне поле\(\vecs{G}(x,y,z)=⟨y,\,x,\,xyz⟩\) консервативним?
- Підказка
-
Перевіряємо поперечні частки.
- Відповідь
-
Ні
Завершуємо цей розділ словом попередження: Перехресна часткова властивість консервативних векторних полів говорить, що якщо\(\vecs{F}\) консервативний, то\(\vecs{F}\) має перехресну часткову властивість. Теорема не говорить про те, що якщо\(\vecs{F}\) має перехресну часткову властивість,\(\vecs{F}\) то консервативна (зворотне імплікації логічно не еквівалентно початковому підтексту). Іншими словами, перехресна часткова властивість консервативних векторних полів може лише допомогти визначити, що поле не є консервативним; це не дозволяє зробити висновок, що векторне поле є консервативним.
Наприклад, розглянемо векторне поле\(\vecs{F}(x,y)=⟨x^2y,\dfrac{x^3}{3}⟩\). Це поле має перехресну часткову властивість, тому природно спробувати використати перехресну часткову властивість консервативних векторних полів, щоб зробити висновок, що це векторне поле є консервативним. Однак це неправильне застосування теореми. Пізніше дізнаємося, як зробити висновок, що\(\vecs F\) є консервативним.
Ключові концепції
- Векторне поле призначає вектор\(\vecs{F}(x,y)\) кожній\((x,y)\) точці\(D\) підмножини\(ℝ^2\) або\(ℝ^3\). \(\vecs{F}(x,y,z)\)до кожної точки\((x,y,z)\) в\(D\) підмножині\(ℝ^3\).
- Векторні поля можуть описувати розподіл векторних величин, таких як сили або швидкості по області площини або простору. Вони широко використовуються в таких областях, як фізика, техніка, метеорологія, океанографія.
- Ми можемо намалювати векторне поле, вивчивши його визначальне рівняння, щоб визначити відносні величини в різних місцях, а потім намалювавши достатньо векторів для визначення візерунка.
- \(\vecs{F}\)Векторне поле називається консервативним, якщо існує скалярна функція\(f\) така, що\(\vecs \nabla f=\vecs{F}\).
Ключові рівняння
- Векторне поле в\(ℝ^2\)
\(\vecs{F}(x,y)=⟨P(x,y),\,Q(x,y)⟩\)
або
\(\vecs{F}(x,y)=P(x,y) \,\hat{\mathbf i}+Q(x,y) \,\hat{\mathbf j}\) - Векторне поле в\(ℝ^3\)
\(\vecs{F}(x,y,z)=⟨P(x,y,z),\,Q(x,y,z),\,R(x,y,z)⟩\)
або
\(\vecs{F}(x,y,z)=P(x,y,z) \,\hat{\mathbf i} +Q(x,y,z) \,\hat{\mathbf j}+R(x,y,z) \,\hat{\mathbf k}\)
Глосарій
- консервативне поле
- векторне поле, для якого існує скалярна функція\(f\) така, що\(\vecs ∇f=\vecs{F}\)
- градієнтне поле
- векторне поле,\(\vecs{F}\) для якого існує скалярна функція\(f\) така, що\(\vecs ∇f=\vecs{F}\); іншими словами, векторне поле, яке є градієнтом функції; такі векторні поля також називаються консервативними
- потенційна функція
- скалярна функція\(f\) така, що\(\vecs ∇f=\vecs{F}\)
- радіальне поле
- векторне поле, в якому всі вектори або вказують безпосередньо в бік або безпосередньо від початку; величина будь-якого вектора залежить тільки від його відстані від початку
- обертальне поле
- векторне поле, в якому вектор в точці\((x,y)\) є дотичною до кола з радіусом\(r=\sqrt{x^2+y^2}\); у обертальному полі всі вектори протікають або за годинниковою стрілкою, або проти годинникової стрілки, і величина вектора залежить тільки від його відстані від початку
- блок векторне поле
- векторне поле, в якому величина кожного вектора дорівнює 1
- векторне поле
- вимірюється в\(ℝ^2\), присвоєння\(\vecs{F}(x,y)\) вектора кожній\((x,y)\) точці\(D\) підмножини\(ℝ^2\); в\(ℝ^3\), присвоєння\(\vecs{F}(x,y,z)\) вектора кожній точці\((x,y,z)\)\(D\) підмножини\(ℝ^3\)
