13.4: Рух у космосі
- Page ID
- 61627
- Опишіть вектори швидкості та прискорення частинки, що рухається у просторі.
- Поясніть тангенціальну і нормальну складові прискорення.
- Державні закони Кеплера руху планет.
Зараз ми бачили, як описувати криві в площині і в просторі, і як визначити їх властивості, такі як довжина дуги і кривизна. Все це призводить до головної мети цієї глави, яка полягає в описі руху по плоских кривих і просторових кривих. Тепер у нас є всі необхідні інструменти; в цьому розділі ми складаємо ці ідеї разом і розглянемо, як їх використовувати.
Вектори руху в площині і в просторі
Нашою відправною точкою є використання векторних функцій для представлення положення об'єкта як функції часу. Всі наведені нижче матеріали можуть бути застосовані або до кривих в площині, або до кривих простору. Наприклад, коли ми дивимось на орбіту планет, криві, що визначають ці орбіти, лежать у площині, оскільки вони еліптичні. Однак частинка, що рухається по спіралі, рухається по кривій у трьох вимірах.
\(\vecs r(t)\)Дозволяти двічі диференційовна векторно-значна функція параметру\(t\), що представляє позицію об'єкта як функцію часу.
Вектор\(\vecs v(t)\) швидкості об'єкта задається
\[\text{Velocity}\,=\vecs v(t)=\vecs r′(t). \label{Eq1} \]
Вектор прискорення\(\vecs a(t)\) визначається як
\[\text{Acceleration}\,=\vecs a(t)=\vecs v′(t)=\vecs r″(t). \label{Eq2} \]
Швидкість визначається бути
\[\mathrm{Speed}\,=v(t)=‖\vecs v(t)‖=‖\vecs r′(t)‖=\dfrac{ds}{dt}. \label{Eq3} \]
Оскільки\(\vecs{r}(t)\) можуть бути як у двох, так і в трьох вимірах, ці векторні функції можуть мати як два, так і три компоненти. У двох вимірах ми визначаємо\(\vecs{r}(t)=x(t) \hat{\mathbf i}+y(t) \hat{\mathbf j}\) і в трьох вимірах\(\vecs r(t)=x(t) \hat{\mathbf i}+y(t) \hat{\mathbf j}+z(t) \hat{\mathbf k}\). Тоді швидкість, прискорення і швидкість можна записати, як показано в наступній таблиці.
| Кількість | Два виміри | Три виміри |
|---|---|---|
| Посада | \(\vecs{r}(t)=x(t) \hat{\mathbf i}+y(t) \hat{\mathbf j}\) | \(\vecs{r}(t)=x(t) \hat{\mathbf i}+y(t) \hat{\mathbf j}+z(t) \hat{\mathbf k}\) |
| Швидкість | \(\vecs{v}(t)=x′(t) \hat{\mathbf i}+y′(t) \hat{\mathbf j}\) | \(\vecs{v}(t)=x′(t) \hat{\mathbf i}+y′(t) \hat{\mathbf j}+z′(t) \hat{\mathbf k}\) |
| Прискорення | \(\vecs{a}(t)=x″(t) \hat{\mathbf i}+y″(t) \hat{\mathbf j}\) | \(\vecs{a}(t)=x″(t) \hat{\mathbf i}+y″(t) \hat{\mathbf j}+z″(t) \hat{\mathbf k}\) |
| Швидкість | \(\|\vecs{v}(t)\|= \sqrt{(x′(t))^2+(y′(t))^2}\) | \(\|\vecs{v}(t)\|=\sqrt{(x′(t))^2+(y′(t))^2+(z′(t))^2}\) |
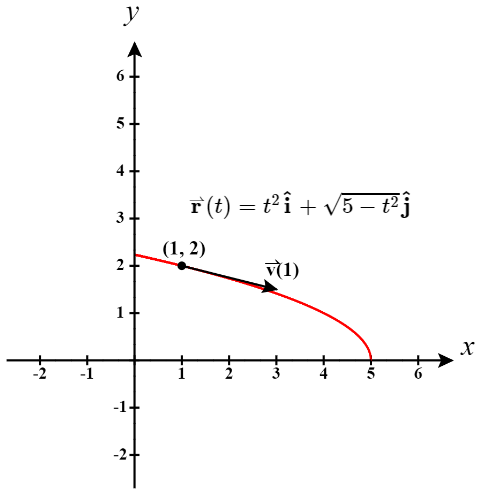
Частинка рухається параболічним шляхом, визначеним векторно-значною функцією\(\vecs{r}(t)=t^2 \hat{\mathbf i}+ \sqrt{5−t^2} \hat{\mathbf j}\), де\(t\) вимірює час у секундах.
- Знайдіть швидкість, прискорення та швидкість як функції часу.
- Намалюйте криву разом з вектором швидкості в часі\(t=1\).
Рішення
- Ми використовуємо рівняння\ ref {Eq1},\ ref {Eq2} і\ ref {Eq3}:
\[ \begin{align*} \vecs{v}(t) &= \vecs{r}′(t)=2t\hat{\mathbf i}−\dfrac{t}{\sqrt{5-t^2}}\hat{\mathbf j} \\[4pt] \vecs{a}(t) &=\vecs{v}′(t)=2\hat{\mathbf i}−5(5−t^2)^{-\frac{3}{2}}\hat{\mathbf j} \\[4pt] ||\vecs{v}(t)|| &=||\vecs{r}′(t)|| \\[4pt] &=\sqrt{(2t)^2+\left(-\dfrac{t}{\sqrt{5-t^2}}\right)^2} \\[4pt] &=\sqrt{4t^2+\dfrac{t^2}{5-t^2}} \\[4pt] &=\sqrt{\dfrac{21t^2-4t^4}{5-t^2}}. \end{align*}\]
- Графік\(\vecs{r}(t)=t^2 \hat{\mathbf i}+ \sqrt{5−t^2} \hat{\mathbf j}\) являє собою частину параболи (рис.\(\PageIndex{1}\)).
Коли\(t=1\),\(\vecs r(1) = (1)^2 \mathbf{\hat i} + \sqrt{5-(1)^2} \mathbf{\hat j} \quad = \quad \mathbf{\hat i} + \sqrt{4} \mathbf{\hat j} \quad = \quad \mathbf{\hat i} + 2 \mathbf{\hat j}\).
Таким чином, частка буде розташована в точці,\((1, 2)\) коли\(t =1\).
Вектор швидкості при\(t=1\) дорівнює\[ \begin{align*} \vecs{v}(1) &=\vecs{r}′(1)=2(1)\hat{\mathbf i}−\frac{1}{\sqrt{5-1^2}} \hat{\mathbf j}\quad \\[4pt] &= \quad 2\hat{\mathbf i}−\frac{1}{2}\hat{\mathbf j} \end{align*}\]
і вектор прискорення\(t=1\) при\[\vecs{a}(1)=\vecs{v}′(1)=2\hat{\mathbf i}−5(5 - 1^2)^{-3/2}\hat{\mathbf j}\quad = \quad 2\hat{\mathbf i}−\frac{5}{8}\hat{\mathbf j}. \nonumber \]
Зверніть увагу, що вектор швидкості дотичний до шляху, як це завжди буває.
Частинка рухається по шляху, визначеному векторною функцією\(\vecs r(t)=(t^2−3t)\,\hat{\mathbf i}+(2t−4)\,\hat{\mathbf j}+(t+2)\,\hat{\mathbf k}\), де\(t\) вимірює час у секундах і де відстань вимірюється у футах. Знайдіть швидкість, прискорення та швидкість як функції часу.
- Підказка
-
Використовуйте рівняння\ ref {Eq1},\ ref {Eq2} та\ ref {Eq3}.
- Відповідь
-
\[\begin{align*}\vecs v(t) &=\vecs{r}'(t) =(2t-3)\,\hat{\mathbf i}+2\,\hat{\mathbf j}+\,\hat{\mathbf k}\\[4pt] \vecs a(t) &=\vecs v′(t) =2\,\hat{\mathbf i} \end{align*}\]
\[ ||\vecs{r}′(t)||=\sqrt{(2t-3)^2+2^2+1^2} =\sqrt{4t^2-12t+14} \nonumber \]
Одиницями швидкості і швидкості є фути в секунду, а одиниці для прискорення - фути в секунду в квадраті.
Щоб краще зрозуміти вектори швидкості та прискорення, уявіть, що ви їдете по кривій дорозі. Якщо ви не повернете кермо, ви б продовжили по прямій лінії і втекли з дороги. Швидкість, з якою ви подорожуєте, коли бігаєте з дороги, укупі з напрямком, дає вектор, що представляє вашу швидкість, як показано на малюнку\(\PageIndex{2}\).
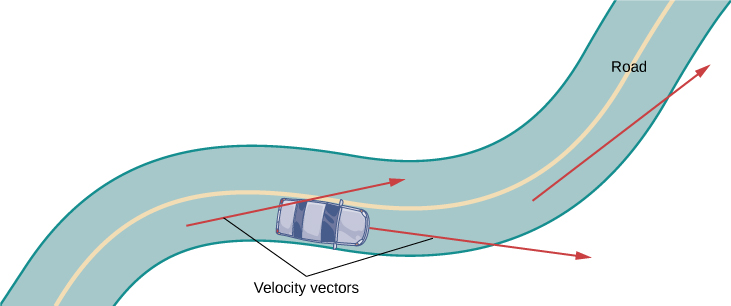
Однак той факт, що ви повинні повернути кермо, щоб залишитися на дорозі, вказує на те, що ваша швидкість завжди змінюється (навіть якщо вашої швидкості немає), тому що ваш напрямок постійно змінюється, щоб тримати вас на дорозі. Коли ви повертаєте праворуч, ваш вектор прискорення також вказує праворуч. Коли ви повертаєте вліво, ваш вектор прискорення вказує ліворуч. Це вказує на те, що ваші вектори швидкості і прискорення постійно змінюються, незалежно від того, чи змінюється ваша реальна швидкість (рис.\(\PageIndex{3}\)).
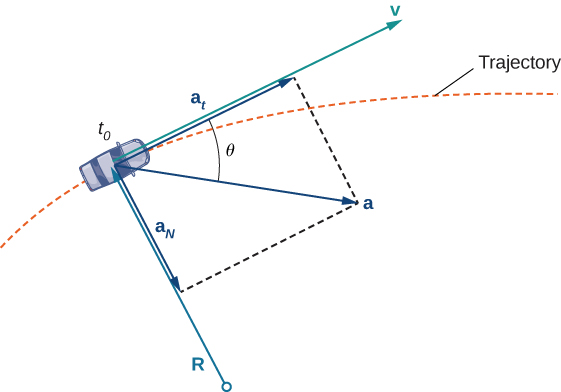
Складові вектора прискорення
Ми можемо об'єднати деякі поняття, розглянуті в розділі Довжина дуги і кривизна з вектором прискорення, щоб отримати більш глибоке розуміння того, як цей вектор відноситься до руху в площині і в просторі. Нагадаємо, що одиничний дотичний вектор\(\vecs T\) і одиничний вектор\(\vecs N\) нормалі утворюють оскулюючу площину в будь-якій\(P\) точці кривої, визначеній векторно-значною функцією\(\vecs{r}(t)\). Наступна теорема показує, що вектор прискорення\(\vecs{a}(t)\) лежить в оскулюлюючій площині і може бути записаний як лінійна комбінація одиничного тангенса і одиничного нормального векторів.
Вектор\(\vecs{a}(t)\) прискорення об'єкта, що рухається по кривій, простеженої двічі диференційовною функцією,\(\vecs{r}(t)\) лежить в площині, утвореній одиничним дотичним вектором\(\vecs T(t)\) і основним одиничним вектором\(\vecs N(t)\) нормалі до\(C\). Крім того,
\[\vecs{a}(t) = v'(t)\vecs{T}(t) + [v(t)]^2 \kappa \vecs{N}(t) \nonumber \]
Тут,\(v(t) = \|\vecs v(t)\|\) є швидкість об'єкта і\(\kappa\) є кривизна\(C\) простежується по\(\vecs{r}(t)\).
Тому що\(\vecs{v}(t)=\vecs{r}′(t)\) і\(\vecs{T}(t)=\dfrac{\vecs{r}′(t)}{||\vecs{r}′(t)||}\), у нас є\(\vecs v(t)=||\vecs{r}′(t)||\vecs{T}(t)=v(t)\vecs{T}(t)\).
Тепер диференціюємо це рівняння:
\[\vecs{a}(t)=\vecs{v}′(t)=\dfrac{d}{dt}\left(v(t)\vecs{T}(t)\right)=v′(t)\vecs{T}(t)+v(t)\vecs{T}′(t) \nonumber \]
Так як\(\vecs{N}(t)=\dfrac{\vecs{T}′(t)}{||\vecs{T}′(t)||}\), ми знаємо\(\vecs{T}′(t)=||\vecs{T}′(t)||\vecs{N}(t)\), так
\[\vecs{a}(t)=v′(t)\vecs{T}(t)+v(t)||\vecs{T}′(t)||\vecs{N}(t). \nonumber \]
Формула кривизни є\(\kappa=\dfrac{||\vecs{T}'(t)||}{||\vecs{r}'(t)||}\), так\(\vecs{T}'(t) = \kappa ||\vecs{r}'(t) || = \kappa v(t) \).
Це дає\(\vecs{a}(t)=v′(t)\vecs{T}(t)+\kappa (v(t))^2 \vecs{N}(t).\)
\(\square\)
Коефіцієнти\(\vecs{T}(t)\) і\(\vecs{N}(t)\) позначаються як тангенціальна складова прискорення і нормальна складова прискорення відповідно. Пишемо\(a_\vecs{T}\) для позначення дотичної складової і\(a_\vecs{N}\) для позначення нормальної складової.
\(\vecs{r}(t)\)Дозволяти векторно-значна функція, яка позначає положення об'єкта як функцію часу. Потім\(\vecs{a}(t)=\vecs{r}′′(t)\) - вектор прискорення. Тангенціальна і нормальна складові прискорення\(a_\vecs{T}\) і\(a_\vecs{N}\) задаються формулами
\[a_{\vecs{T}}=\vecs a \cdot\vecs{T}=\dfrac{\vecs{v}\cdot\vecs{a}}{||\vecs{v}||} \label{Eq1B} \]
і
\[a_\vecs{N}=\vecs a\cdot \vecs N=\dfrac{||\vecs v \times \vecs a||}{||\vecs v||}=\sqrt{||\vecs a||^2−{\left(a_{\vecs{T}}\right)^2}}. \label{Eq2B} \]
Ці компоненти пов'язані за формулою
\[\vecs{a}(t)=a_\vecs{T} \vecs{T}(t)+a_\vecs{N}\vecs{N}(t). \label{Eq3B} \]
\(\vecs{T}(t)\)Ось вектор дотичної одиниці до кривої\(\vecs{r}(t)\), визначеної, і\(\vecs{N}(t)\) є одиничним нормальним вектором до кривої, визначеної\(\vecs{r}(t)\).
Нормальну складову прискорення також називають доцентровою складовою прискорення або іноді радіальною складовою прискорення. Щоб зрозуміти доцентрове прискорення, припустимо, що ви їдете на автомобілі по круговій трасі з постійною швидкістю. Потім, як ми бачили раніше, вектор прискорення завжди вказує на центр доріжки. Як вершник у машині, ви відчуваєте тягу до зовнішньої частини траси, тому що ви постійно повертаєте. Це відчуття діє в протилежному напрямку доцентрового прискорення. Те ж саме стосується некруглих доріжок. Причина полягає в тому, що ваше тіло має тенденцію подорожувати по прямій лінії і чинить опір силі, що виникає в результаті прискорення, яке штовхає його в бік. Зверніть увагу, що\(B\) в точці на\(\PageIndex{4}\) малюнку вектор прискорення спрямований назад. Це пов'язано з тим, що автомобіль сповільнюється, коли він йде в криву.
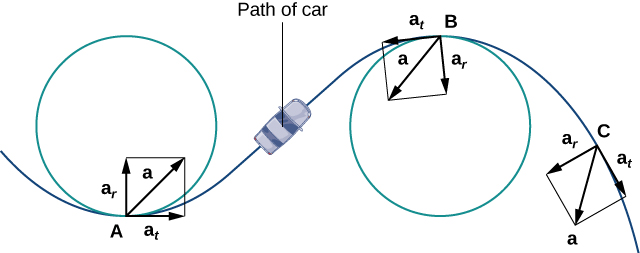
Тангенціальний і нормальний одиничні вектори в будь-якій заданій точці кривої забезпечують систему відліку в цій точці. Тангенціальна і нормальна складові прискорення є проекціями вектора прискорення на\(\vecs T\) і\(\vecs N\), відповідно.
Частинка рухається по шляху, визначеному векторно-значною функцією\(\vecs{r}(t)=t^2\,\hat{\mathbf i}+(2t−3)\,\hat{\mathbf j}+(3t^2−3t)\,\hat{\mathbf k}\), де\(t\) вимірює час у секундах, а відстань вимірюється у футах.
- Знайти\(a_\vecs{T}\) і\(a_\vecs{N}\) як функції\(t\).
- Знайти\(a_\vecs{T}\) і\(a_\vecs{N}\) вчасно\(t=2\).
Рішення
- Почнемо виводити функції швидкості і прискорення:
\[\begin{align*} \vecs{v}(t) &= \vecs{r}'(t) \\[4pt] &= 2t\,\hat{\mathbf i}+2\,\hat{\mathbf j}+(6t-3)\,\hat{\mathbf k} \\[4pt] \vecs{a}(t) &= \vecs{v}'(t) \\[4pt] &=2\,\hat{\mathbf i}+6\,\hat{\mathbf k} \end{align*}\]Тепер ми застосовуємо Рівняння\ ref {Eq1B}:\[\begin{align*}a_{\vecs{T}} &=\dfrac{\vecs{v}\cdot \vecs{a}}{||\vecs{v} ||} \\[4pt] &= \dfrac{ (2t \,\hat{\mathbf i} +2\,\hat{\mathbf j} +(6t-3)\,\hat{\mathbf k})\cdot(2\,\hat{\mathbf i}+6\,\hat{\mathbf k}) }{|| 2t\,\hat{\mathbf i} + 2\,\hat{\mathbf j} + (6t-3)\,\hat{\mathbf k} ||} \\[4pt] &= \dfrac{4t + 6(6t-3)}{\sqrt{(2t)^2 +2^2 + (6t-3)^2}} \\[4pt] &= \dfrac{40t-18}{40t^2 - 36t+13} \end{align*}\] Тепер ми можемо застосувати рівняння\ ref {Eq2B}:
\[\begin{align*} a_\vecs{N} &=\sqrt{||\vecs{a}||^2-\left(a_{\vecs{T}}\right)^2} \\[4pt] &= \sqrt{||2\,\hat{\mathbf i}+6\,\hat{\mathbf k}||^2 - \left( \dfrac{ 40t-18 }{\sqrt{40t^2-36t+13}} \right)^2} \\[4pt] &= \sqrt{ 4+36-\dfrac{(40t-18)^2}{40t^2-36t+13} } \\[4pt] &= \sqrt{\dfrac{ 40(40t^2-36t+13)-(1600t^2-1440t+324) }{40t^2-36t+13} } \\[4pt] &= \sqrt{ \dfrac{196}{ 40t^2-36t+13} } \\[4pt] &= \dfrac{14}{\sqrt{40t^2-36t+13}} \end{align*}\]
- Ми повинні оцінити кожну з відповідей з частини а за адресою\(t=2\):
\[\begin{align*} a_{\vecs{T}}(2) &= \dfrac{ 40(2)-18 }{\sqrt{40(2)^2 - 36(2)+13 }} \\[4pt] &= \dfrac{80-18 }{\sqrt{160-72+13}} \\[4pt] &= \dfrac{62}{\sqrt{101}} \\[4pt] a_{\vecs{N}}(2) &= \dfrac{14}{\sqrt{40(2)^2 -36(2)+13 }} \\[4pt] &= \dfrac{14}{\sqrt{160-72+13}} = \dfrac{14}{\sqrt{101}}. \end{align*}\]
Одиницями прискорення є фути на секунду в квадраті, як і одиниці нормальної та тангенціальної складових прискорення.
Об'єкт рухається по шляху, визначеному векторною функцією\(\vecs r(t)=4t\,\hat{\mathbf i}+t^2\,\hat{\mathbf j}\), де\(t\) вимірює час у секундах.
- Знайти\(a_\vecs{T}\) і\(a_\vecs{N}\) як функції\(t\).
- Знайти\(a_\vecs{T}\) і\(a_\vecs{N}\) вчасно\(t=−3\).
- Підказка
-
Використовувати рівняння\ ref {Eq1B} і\ ref {Eq2B}
- Відповідь
-
а.\[\begin{align*} a_\vecs{T} =\dfrac{\vecs v(t) \cdot \vecs a(t)}{||\vecs v(t)||}= \dfrac{\vecs r'(t) \cdot \vecs r''(t) }{||\vecs r'(t)||} \\ = \dfrac{ (4\,\hat{\mathbf i} + 2t \,\hat{\mathbf j}) \cdot (2\,\hat{\mathbf j}) }{||4\,\hat{\mathbf i} + 2t \,\hat{\mathbf j} ||} \\ = \dfrac{4t}{\sqrt{4^2 + (2t)^2}}\\ = \dfrac{2t}{\sqrt{2+t^2}} \end{align*}\]
\[\begin{align*} a_\vecs{N} = \sqrt{||\vecs a||^2-a_\vecs{T}^2}\\ =\sqrt{||2\,\hat{\mathbf j} ||^2 - \left(\dfrac{2t}{\sqrt{2+t^2}}\right)^2} \\ =\sqrt{ 4 - \dfrac{4t^2 }{2+t^2} } \end{align*}\]б.\[\begin{align*} a_\vecs{T}(−3) = \dfrac{2(-3)}{\sqrt{2+(-3)^2}} \\ = \dfrac{-6}{\sqrt{11}}\end{align*}\]
\[\begin{align*}a_\vecs{N}(−3) = \sqrt{ 4 - \dfrac{4(-3)^2 }{2+(-3)^2} } \\ = \sqrt{4- \dfrac{36}{11}} \\ = \sqrt{\dfrac{8}{11} }\\ =\dfrac{2\sqrt{2}}{\sqrt{11}} \end{align*}\]
рух снаряда
Тепер давайте розглянемо застосування векторних функцій. Зокрема, розглянемо вплив сили тяжіння на рух об'єкта під час його переміщення по повітрю, і як він визначає результуючу траєкторію цього об'єкта. Далі ми ігноруємо вплив опору повітря. Ця ситуація, коли об'єкт рухається з початковою швидкістю, але без сил, що діють на нього, крім сили тяжіння, відома як рух снаряда. Він описує рух об'єктів від м'ячів для гольфу до бейсболів, і від стрілок до гарматних ядер.
Для початку нам потрібно вибрати систему координат. Якщо ми стоїмо біля початку цієї системи координат, то вибираємо позитивну\(y\) -вісь бути вгору, негативна\(y\) - вісь повинна бути вниз, а позитивна\(x\) - вісь бути вперед (тобто подалі від метальника об'єкта). Ефект гравітації знаходиться в напрямку вниз, тому другий закон Ньютона говорить нам, що сила на об'єкт, що виникає внаслідок гравітації, дорівнює масі об'єкта, що разів перевищує прискорення, що виникає в результаті гравітації\(\vecs F_g=m\vecs a\), або, де\(\vecs F_g\) представляє силу тяжіння і\(\vecs a = -g\,\hat{\mathbf j}\) представляє прискорення в результаті гравітації на поверхні Землі. Значення\(g\) в англійській системі вимірювання становить приблизно 32 футів/сек 2 і це приблизно 9,8 м/сек 2 в метричній системі. Це єдина сила, що діє на об'єкт. Оскільки гравітація діє в напрямку вниз, ми можемо записати силу, що виникає в результаті гравітації\(\vecs F_g=−mg\,\hat{\mathbf j}\), у вигляді, як показано на малюнку\(\PageIndex{5}\).
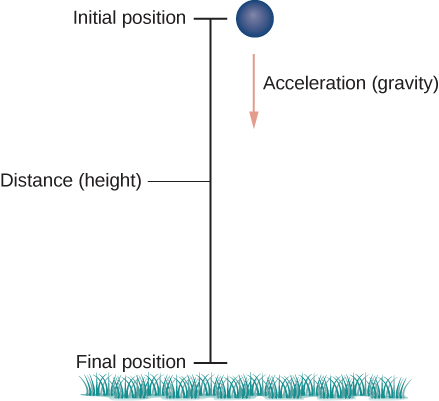
Другий закон Ньютона також говорить нам про те\(F=m\vecs{a}\), де\(\vecs a\) представляє вектор прискорення об'єкта. Ця сила повинна бути рівною силі тяжіння в усі часи, тому ми знаємо, що
\[\begin{align*} \vecs F =\vecs F_g \\ m\vecs{a} = -mg \,\hat{\mathbf j} \\ \vecs{a} = -g\,\hat{\mathbf j}. \end{align*}\]
Тепер скористаємося тим, що вектор прискорення є першою похідною вектора швидкості. Тому ми можемо переписати останнє рівняння у вигляді
\[\vecs v'(t) = -g\,\hat{\mathbf j} \nonumber \]
Взявши антипохідну кожної сторони цього рівняння, отримаємо
\[ \vecs v(t) = \int -g \,\hat{\mathbf j}\; dt = -gt\,\hat{\mathbf j} + \vecs C_1 \nonumber \]
для деякого константного вектора\(\vecs C_1\). Для визначення значення цього вектора ми можемо використовувати швидкість об'єкта в фіксований час, скажімо в момент часу\(t=0\). Ми називаємо цю швидкість початковою швидкістю:\(\vecs v(0)=\vecs v_0\). Тому\(\vecs v(0)=−g(0)\,\hat{\mathbf j}+\vecs C_1=\vecs v_0\) і\(\vecs C_1= \vecs v_0\). Це дає вектор швидкості як\(\vecs v(t)=−gt\,\hat{\mathbf j}+\vecs v_0\).
Далі ми використовуємо той факт, що швидкість\(\vecs{v}(t)\) є похідною від положення\(\vecs{s}(t)\). Це дає рівняння
\[\vecs s'(t)=-gt\,\hat{\mathbf j}+\vecs{v}_0. \nonumber \]
Прийняття антипохідного обох сторін цього рівняння призводить до
\[\begin{align*} \vecs s(t) &= \int -gt\,\hat{\mathbf j} + \vecs{v}_0 \;dt \\[4pt] &= -\dfrac{1}{2}gt^2 \,\hat{\mathbf j} + \vecs{v}_0 t + \vecs{C}_2 \end{align*}\]
з іншим невідомим константним вектором\(\vecs{C}_2\). Щоб визначити значення\(\vecs{C}_2\), ми можемо використовувати положення об'єкта в даний момент часу, скажімо в момент часу\(t=0\). Називаємо цю позицію вихідним положенням:\(\vecs{s}(0)=\vecs{s}_0\). Тому,\(\vecs{s}(0)=−(1/2)g(0)^2\,\hat{\mathbf j}+\vecs{v}_0(0)+\vecs{C}_2=\vecs{s}_0\). Це дає положення об'єкта в будь-який час, як
\[ \vecs{s}(t)=−\dfrac{1}{2}gt^2 \,\hat{\mathbf j}+\vecs{v}_0 t+\vecs{s}_0. \nonumber \]
Давайте докладніше розглянемо початкову швидкість і початкове положення. Зокрема, припустимо, що об'єкт перекинутий вгору від початку під кутом\(\theta\) до горизонталі, з початковою швидкістю\(\vecs{v}_0\). Як ми можемо змінити попередній результат, щоб відобразити цей сценарій? По-перше, можна припустити, що він викинутий від походження. Якщо ні, то ми можемо перемістити початок до точки, звідки вона кинута. Тому\(\vecs{s}_0=\vecs{0}\), як показано на рис\(\PageIndex{6}\).
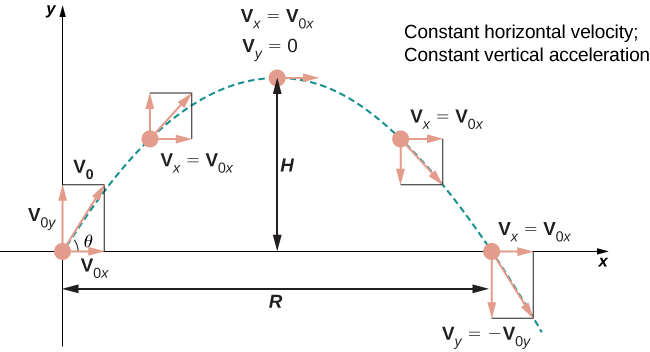
Ми можемо переписати початковий вектор швидкості у вигляді\(\vecs{v}_0= v_0 \cos \theta \,\hat{\mathbf i} + v_0 \sin \theta \,\hat{\mathbf j}\). Тоді рівняння для функції положення\(\vecs{s}(t)\) стає
\[\begin{align*} \vecs{s}(t) &=-\dfrac{1}{2} gt^2\,\hat{\mathbf j} + v_0 t \cos\theta \,\hat{\mathbf i} + v_0 t \sin\theta \,\hat{\mathbf j} \\[4pt] &= v_0 t \cos\theta\,\hat{\mathbf i} + v_0 t \sin\theta \,\hat{\mathbf j} - \dfrac{1}{2} gt^2\,\hat{\mathbf j} \\[4pt] &= v_0 t \cos\theta \,\hat{\mathbf i} + \left(v_0 t \sin\theta - \dfrac{1}{2} gt^2\right)\,\hat{\mathbf j}. \end{align*}\]
Коефіцієнт\(\hat{\mathbf i}\) представляє горизонтальну складову\(\vecs{s}(t)\) і є горизонтальною відстанню об'єкта від початку в часі\(t\). Максимальне значення горизонтальної відстані (вимірюється на тій же початковій і кінцевій висоті) називається діапазоном\(R\). Коефіцієнт\(\hat{\mathbf j}\) представляє вертикальну складову\(\vecs{s}(t)\) і є висотою об'єкта в часі\(t\). Максимальне значення відстані по вертикалі - висота\(H\).
Під час святкування Дня незалежності гарматне ядро вистрілюється з гармати на скелі до води. Гармата спрямована на кут 30° над горизонталлю, а початкова швидкість гарматного ядра становить 600 футів/сек. Скеля знаходиться на 100 футів над водою (рис.\(\PageIndex{7}\)).
- Знайдіть максимальну висоту гарматного ядра.
- Скільки часу займе гарматне ядро, щоб виплескатися в море?
- Як далеко до моря гарматне ядро вдарить у воду?
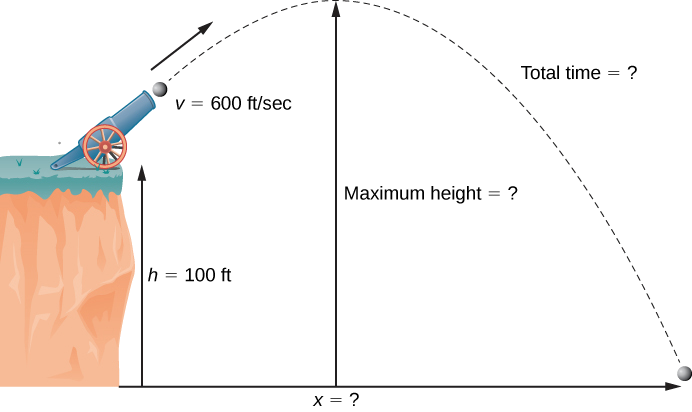
Рішення
Використовуємо рівняння
\[\vecs{s}(t) = v_0 t \cos\theta \,\hat{\mathbf i} + \left(v_0 t \sin\theta - \dfrac{1}{2}gt^2 \right)\,\hat{\mathbf j} \nonumber \]
з\(\theta=30^\circ \),\(g=32 \dfrac{\text{ft}}{\text{sec}^2}\), і\(v_0=600 \dfrac{\text{ft}}{\text{sec}^2}\). Тоді рівняння положення стає
\[\begin{align*} \vecs{s}(t) &= 600 t ( \cos 30^\circ)\,\hat{\mathbf i} + \left(600t \sin30^\circ - \dfrac{1}{2}(32)t^2 \right)\,\hat{\mathbf j} \\[4pt] &= 300t\sqrt{3} \,\hat{\mathbf i} + \left( 300t - 16t^2 \right)\,\hat{\mathbf j} \end{align*}\]
- Гарматне ядро досягає своєї максимальної висоти, коли вертикальна складова його швидкості дорівнює нулю, оскільки гарматне ядро не піднімається і не падає в цій точці. Вектор швидкості дорівнює
\[\begin{align*} \vecs{v}(t) &=\vecs s'(t)\\[4pt] &= 300 \sqrt{3} \,\hat{\mathbf i} + (300-32t)\,\hat{\mathbf j} \end{align*} \nonumber \]
Тому вертикальна складова швидкості задається виразом\(300−32t\). Встановлення цього виразу рівним нулю і розв'язування для t дає\(t=9.375\) сек. Висота гарматного ядра в цей час задається вертикальною складовою вектора положення, оцінюється при\(t=9.375\).\[\begin{align*} \vecs{s}(9.375) &=300(9.375)\sqrt{3}\,\hat{\mathbf i}+(300(9.375)−16(9.375)^2)\,\hat{\mathbf j} \\[4pt] &=4871.39 \,\hat{\mathbf i}+1406.25\,\hat{\mathbf j} \end{align*}\]
Тому максимальна висота гарматного ядра становить 1406,39 футів над гарматою, або 1506,39 футів над рівнем моря. - Коли гарматне ядро приземляється у воді, воно знаходиться на 100 футів нижче гармати. Отже, вертикальна складова вектора положення дорівнює −100. Встановлюючи вертикальну складову\(\vecs s(t)\) рівною −100 та розв'язуючи, отримаємо
\[\begin{align*} 300t-16t^2 &= -100 \\ 16t^2-300t-100 =0 \\4t^2-75-25 =0 \\[4pt] t &= \dfrac{75\pm \sqrt{(-75)^2}-4(4)(-25) }{2(4)} \\[4pt] &= \dfrac{75 \pm \sqrt{6025}}{8} \\[4pt] &= \dfrac{75 \pm 5\sqrt{241}}{8} \end{align*}\]
Позитивне значення\(t\), яке вирішує це рівняння, становить приблизно 19.08. Тому гарматне ядро потрапляє в воду приблизно через 19,08 сек. - Щоб знайти відстань до моря, ми просто підставляємо відповідь з частини (b) на\(\vecs{s}(t)\):
\[\begin{align*} \vecs s(19.08) &=300(19.08)\sqrt{3} \,\hat{\mathbf i}+\left(300(19.08)−16(19.08)^2\right)\,\hat{\mathbf j}\\[4pt] &=9914.26\,\hat{\mathbf i}−100.7424\,\hat{\mathbf j} \end{align*}\]
Тому м'яч потрапляє у воду приблизно на 9914,26 футів від основи скелі. Зверніть увагу, що вертикальна складова вектора позиції дуже близька до −100, що говорить нам про те, що м'яч просто вдарив воду. Зверніть увагу, що 9914.26 футів не є справжньою дальністю гармати, оскільки гарматне ядро приземляється в океані в місці нижче гармати. Дальність гармати буде визначатися, знайшовши, наскільки далеко гарматне ядро, коли його висота 100 футів над водою (так само, як висота гармати).
Стрілець стріляє стрілою під кутом 40° над горизонталлю з початковою швидкістю 98 м/сек. Висота лучника - 171,5 см. Знайдіть горизонтальну відстань, яку стрілка подорожує, перш ніж вона потрапить на землю.
- Підказка
-
Рівняння вектора положення потрібно враховувати висоту лучника в метрах.
- Відповідь
-
967.15 км
Залишається останнє питання: Загалом, яку максимальну відстань може проїхати снаряд, враховуючи його початкову швидкість? Щоб визначити цю відстань, припускаємо, що снаряд випущений з рівня землі і бажаємо, щоб він повернувся на рівень землі. Іншими словами, ми хочемо визначити рівняння для діапазону. При цьому рівняння руху снаряда дорівнює
\[\vecs{s}=v_0 t \cos\theta \,\hat{\mathbf i} + \left(v_0t\sin\theta - \dfrac{1}{2}gt^2 \right)\,\hat{\mathbf j}. \nonumber \]
Встановлення другої складової рівної нулю та рішення для\(t\) прибутковості
\[\begin{align*} v_0 t \sin\theta - \dfrac{1}{2}gt^2 =0\\ t\left(v_0 \sin\theta - \dfrac{1}{2}gt\right) =0 \end{align*}\]
Тому або\(t=0\) або\(t=\dfrac{2v_0\sin\theta}{g}\). Нас цікавить друге значення\(t\), тому ми підставляємо це в\(\vecs{s}(t)\), який дає
\[\begin{align*} \vecs{s}\left(\dfrac{2v_0\sin\theta}{g} \right) = v_0 \left(\dfrac{2v_0\sin\theta}{g} \right) \cos\theta \,\hat{\mathbf i} + \left( v_0\left(\dfrac{2v_0\sin\theta}{g} \right)\sin\theta - \dfrac{1}{2}g\left(\dfrac{2v_0\sin\theta}{g} \right)^2 \right)\,\hat{\mathbf j} \\ = \left(\dfrac{2v_0^2\sin\theta\cos\theta}{g} \right)\,\hat{\mathbf i} \\ = \dfrac{v_0^2 \sin2\theta}{g}\,\hat{\mathbf i}. \end{align*}\]
Таким чином, вираз для дальності снаряда, випущеного під кутом\(\theta\), є
\[R=\dfrac{v_0^2 \sin2\theta}{g}\,\hat{\mathbf i} . \nonumber \]
Єдиною змінною в цьому виразі є\( \theta\). Щоб максимально збільшити пройдену відстань, візьміть похідну від коефіцієнта i по відношенню до\(\theta\) і встановіть його рівним нулю:
\[\begin{align*} \dfrac{d}{d\theta} \left( \dfrac{v_0^2 \sin2\theta}{g} \right) =0\\ \dfrac{2v_0^2\cos2\theta}{g} =0\\ \theta=45^\circ \end{align*}\]
Це значення\(\theta)\) є найменшим додатним значенням, яке робить похідну рівною нулю. Тому при відсутності опору повітря найкращий кут для стрільби снарядом (для максимальної дальності) знаходиться під кутом 45°. Відстань, яку вона проходить, задається
\[\vecs{s}\left(\dfrac{2v_0 \sin 45^\circ}{g} \right)= \dfrac{v_0^2 \sin 90^\circ}{g} \,\hat{\mathbf i} = \dfrac{v_0^2}{g}\,\hat{\mathbf i} \nonumber \]
Тому діапазон для кута 45° дорівнює\(\frac{v_0^2}{g}\) одиницям.
Закони Кеплера
На початку 1600-х років Йоганнес Кеплер зміг використати дивно точні дані свого наставника Тихо Браге, щоб сформулювати свої три закони руху планет, тепер відомі як закони руху планет Кеплера. Ці закони також застосовуються до інших об'єктів Сонячної системи на орбіті навколо Сонця, таких як комети (наприклад, комета Галлея) та астероїди. Варіації цих законів застосовуються до супутників на орбіті навколо Землі.
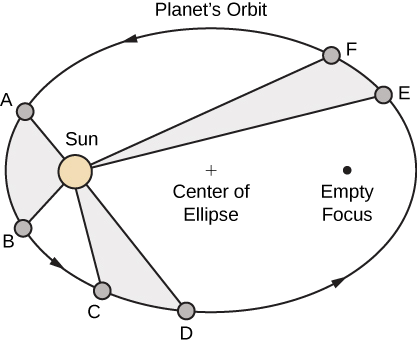
- Шляхи будь-якої планети навколо Сонця мають еліптичну форму, при цьому центр Сонця розташований в одному фокусі еліпса (закон еліпсів).
- Лінія, проведена від центру Сонця до центру планети, змітає рівні ділянки через рівні проміжки часу (закон рівних площ) (рис.\(\PageIndex{8}\)).
- Співвідношення квадратів періодів будь-яких двох планет дорівнює відношенню кубів довжин їх напіввеликих орбітальних осей (Закон Гармоній).
Третій закон Кеплера особливо корисний при використанні відповідних одиниць. Зокрема, 1 астрономічна одиниця визначається як середня відстань від Землі до Сонця, і в даний час визнана 149 597 870,700 м або, приблизно 93 000 000 миль. Тому ми пишемо 1 А.У. = 93 000 000 миль. Оскільки час, який потрібен Землі на орбіту Сонця, становить 1 рік, ми використовуємо земні роки для одиниць часу. Тоді, підставивши 1 рік на період Землі і 1 а.у. на середню відстань до Сонця, третій закон Кеплера можна записати як
\[ T_p^2=D_p^3 \nonumber \]
для будь-якої планети Сонячної системи, де\(T_P\) період цієї планети вимірюється в роках Землі і середня відстань від\(D_P\) цієї планети до Сонця, виміряна в астрономічних одиницях. Тому, якщо ми знаємо середню відстань від планети до Сонця (в астрономічних одиницях), то можна потім обчислити довжину її року (в земних роках), і навпаки.
Закони Кеплера були сформульовані на основі спостережень Браге; однак вони не були доведені формально, поки сер Ісаак Ньютон не зміг застосувати обчислення. Крім того, Ньютон зміг узагальнити третій закон Кеплера на інші орбітальні системи, такі як Місяць, що обертається навколо планети. Початковий третій закон Кеплера застосовується лише до об'єктів, що обертаються навколо Сонця.
Давайте тепер доведемо перший закон Кеплера, використовуючи обчислення векторно-значних функцій. Для початку нам потрібна система координат. Давайте розмістимо Сонце в початок системи координат і нехай векторна функція\(\vecs{r}(t)\) представляє розташування планети як функцію часу. Ньютон довів закон Кеплера, використовуючи свій другий закон руху і його закон всесвітнього тяжіння. Другий закон руху Ньютона можна записати як\(\vecs{F}=m\vecs{a}\), де\(\vecs{F}\) являє собою чисту силу, що діє на планету. Його закон всесвітнього тяжіння можна записати в формі\(\vecs{F}=−\dfrac{GmM}{||\vecs{r}||^2}\cdot \dfrac{\vecs{r}}{||\vecs{r} ||}\), яка вказує на те, що сила, що виникає в результаті гравітаційного тяжіння Сонця, вказує назад до Сонця, і має величину\(\dfrac{GmM}{||\vecs{r}||^2} \) (рис.\(\PageIndex{9}\)).
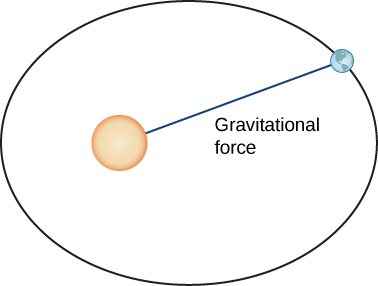
Встановлюючи ці дві сили рівні один одному, і використовуючи те\(\vecs a(t)=\vecs v′(t)\), що, отримуємо
\[ m\vecs v′(t)=−\frac{GmM}{‖\vecs r‖^2}⋅\frac{\vecs r}{‖\vecs r‖}, \nonumber \]
які можна переписати як
\[ \dfrac{d\vecs v}{dt}=−\dfrac{GM}{||\vecs r||^3}\vecs{r}. \nonumber \]
Це рівняння показує, що\(\vecs r\) вектори\(d\vecs{v}/dt\) і паралельні один одному, так\(d\vecs {v}/dt \times \vecs {r}=\vecs 0\). Далі давайте\(\vecs{r} \times \vecs{v}\) розмежовуємо щодо часу:
\[\dfrac{d}{dt}(\vecs{r}\times \vecs{v})=\dfrac{d\vecs{r}}{dt}\times \vecs v+\vecs{r} \times \dfrac{d\vecs{v}}{dt}=\vecs{v}\times \vecs{v}+\vecs{0}=\vecs{0}. \label{Eq10} \]
Це доводить, що\(\vecs{r}\times\vecs{v}\) є постійним вектором, який ми називаємо\(\vecs C\). Оскільки\(\vecs r\) і\(\vecs v\) обидва перпендикулярні\(\vecs C\) для всіх значень\(t\), вони повинні лежати в перпендикулярній площині\(\vecs C\). Тому рух планети лежить в площині.
Далі обчислюємо вираз\(d\vecs{v}/dt\times \vecs C\):
\[\dfrac{d\vecs{v}}{dt} \times \vecs{C}=−\dfrac{GM}{||\vecs{r}||^3}\vecs{r}\times (\vecs{r}\times\vecs{v})=−\dfrac{GM}{||\vecs r||^3}[(\vecs{r} \cdot \vecs{v})\vecs{r} - (\vecs{r} \cdot \vecs{r})\vecs{v}]. \label{Eq11} \]
Остання рівність у Equation\ ref {Eq10} походить від формули потрійного перехресного добутку (Вступ до векторів у просторі). Нам потрібен вираз для\(\vecs{r}\cdot \vecs{v}\). Щоб обчислити це,\(\vecs{r}\cdot \vecs{r}\) диференціюємо щодо часу:
\[ \dfrac{d}{dt}(\vecs{r}\cdot \vecs{r})=\dfrac{d\vecs{r}}{dt}\cdot \vecs{r}+\vecs{r}\cdot \dfrac{d\vecs{r}}{dt}=2\vecs{r}\cdot \dfrac{d\vecs{r}}{dt}=2\vecs{r}\cdot \vecs{v}. \label{Eq12} \]
З тих пір\(\vecs{r}\cdot\vecs{r}=||\vecs r||^2\), у нас також є
\[\dfrac{d}{dt}(\vecs{r}\cdot \vecs{r})=\dfrac{d}{dt}||\vecs{r}||^2=2||\vecs{r}|| \dfrac{d}{dt}||\vecs{r}||. \label{Eq13} \]
Поєднуючи рівняння\ ref {Eq12} і рівняння\ ref {Eq13}, отримаємо
\[\begin{align*} 2\vecs{r}\cdot \vecs{v} =2||\vecs{r}||\dfrac{d}{dt}||\vecs{r}|| \\ \vecs{r} \cdot \vecs{v} =||\vecs{r}‖\dfrac{d}{dt}||\vecs{r}||. \end{align*} \label{Eq14} \]
Підставляючи це в рівняння\ ref {Eq11} дає нам
\[\begin{align} \dfrac{d\vecs{v}}{dt} \times \vecs{C} = - \dfrac{GM}{||\vecs{r}||^3} [(\vecs{r}\cdot \vecs{v})\vecs{r} - (\vecs{r}\cdot \vecs{r})\vecs{v}] \nonumber \\ = -\dfrac{GM}{||\vecs{r}||^3}\left[ ||\vecs{r} \left(\dfrac{d}{dt} ||\vecs{r}||\right)\vecs{r} - ||\vecs{r}||^2\vecs{v} \right] \nonumber \\ = -GM\left[ \dfrac{1}{||\vecs{r}||^2}\left( \dfrac{d}{dt} ||\vecs{r}|| \right)\vecs{r} - \dfrac{1}{||\vecs{r}||}\vecs{v} \right] \nonumber \\ = GM\left[ \dfrac{\vecs{v}}{||\vecs{r}||} -\dfrac{\vecs{r}}{||\vecs{r}||^2}\left( \dfrac{d}{dt} ||\vecs{r}|| \right) \right]. \label{Eq15} \end{align} \]
Однак,
\[ \begin{align*} \dfrac{d}{dt} \dfrac{\vecs{r}}{||\vecs{r}||} = \dfrac{ \frac{d}{dt}(\vecs{r})||\vecs{r}||- \vecs{r}\frac{d}{dt}||\vecs{r}|| }{||\vecs{r}||^2} \\ = \dfrac{ \frac{d\vecs{r}}{dt} }{||\vecs{r}||} - \dfrac{\vecs{r}}{||\vecs{r}||^2}\dfrac{d}{dt}||\vecs{r} || \\ = \dfrac{\vecs{v}}{||\vecs{r}||} - \dfrac{\vecs{r}}{||\vecs{r}||^2} \dfrac{d}{dt}||\vecs{r}||. \end{align*}\]
Таким чином, рівняння\ ref {Eq15} стає
\[\dfrac{d \vecs{v}}{dt}\times \vecs{C}=GM\left( \dfrac{d}{dt}\dfrac{ \vecs{r}}{ || \vecs{r} ||} \right).\nonumber \]
Оскільки\(\vecs{C}\) це постійний вектор, ми можемо інтегрувати обидві сторони та отримати
\[ \vecs{v}\times\vecs{C} = GM \dfrac{ \vecs{r} }{|| \vecs{r} ||} + \vecs{D}, \nonumber \]
де\(\vecs D\) постійний вектор. Наша мета - вирішити для\(|| \vecs{r} ||\). Почнемо з розрахунку\( \vecs{r} \cdot ( \vecs{v}\times \vecs{C}\):
\[\vecs{r} \cdot ( \vecs{v}\times \vecs{C} =GM\dfrac{||\vecs{r}||^2}{||\vecs{r}||}+ \vecs{r}\cdot\vecs{D} =GM||\vecs{r}||+\vecs{r}\cdot \vecs{D}. \nonumber \]
Однак\( \vecs{r} \cdot ( \vecs{v}\times \vecs{C})= ( \vecs{r} \times \vecs{v})\cdot \vecs{C} \), так
\[ ( \vecs{r} \times \vecs{v})\cdot \vecs{C} =GM||\vecs{r}|| + \vecs{r}\cdot \vecs{D}.\nonumber \]
З тих пір\(\vecs{r}\times \vecs{v}=\vecs{C}\), у нас є
\[ ||\vecs{C}||^2 =GM||\vecs{r}|| +\vecs{r}\cdot \vecs{D}.\nonumber \]
Зверніть увагу на те\( \vecs{r} \cdot \vecs{D}=||\vecs{r}|| ||\vecs{D}||\cos \theta \), де\(\theta\) знаходиться кут між\(\vecs{r}\) і\(\vecs{D}\). Тому
\[ ||\vecs{C}||^2=GM||\vecs{r}||+||\vecs{r}|| ||\vecs{D}|| \cos\theta \nonumber \]
Рішення для\(||\vecs{r}||\),
\[ ||\vecs{r}|| = \dfrac{||\vecs{C}||^2 }{GM+||\vecs{D}||\cos\theta} = \dfrac{||\vecs{C}||^2}{GM}\left( \dfrac{1}{1+e\cos\theta} \right). \nonumber \]
де\(e=||\vecs{D}||/GM\). Це полярне рівняння конічного конуса з фокусом на початку, яке ми встановили як Сонце. Це гіпербола\(e>1\), якщо, парабола\(e=1\), якщо, або еліпс, якщо\(e<1\). Оскільки планети мають замкнуті орбіти, єдина можливість - еліпс. Однак на цьому етапі слід згадати, що гіперболічні комети дійсно існують. Це об'єкти, які просто проходять через Сонячну систему зі швидкістю, занадто великою, щоб потрапити в пастку на орбіту навколо Сонця. Коли вони проходять досить близько до Сонця, гравітаційне поле Сонця відхиляє траєкторію настільки, що шлях стає гіперболічним.
\(\square\)
Третій закон руху планети Кеплера може бути змінений у випадку одного об'єкта на орбіті навколо об'єкта, відмінного від Сонця, наприклад, Місяця навколо Землі. У цьому випадку третім законом Кеплера стає
\[P^2 = \dfrac{4\pi^2 a^3}{G(m+M)}, \label{Eq30} \]
де m - маса Місяця, а M - маса Землі, a являє собою довжину великої осі еліптичної орбіти, а P - період.
З огляду на, що маса Місяця становить\(7.35\times 10^{22}\) кг, маса Землі -\(5.97\times 10^{24}\) кг\(G=6.67\times 10^{−11} \text{m} / \text{kg} \cdot \text{sec}^2\), а період Місяця - 27,3 дня, знайдемо довжину великої осі орбіти Місяця навколо Землі.
Рішення
Важливо бути узгодженим з одиницями. Оскільки універсальна гравітаційна константа містить секунди в одиницях, нам також потрібно використовувати секунди для періоду Місяця:
\[27.3 \; \text{days} \times \dfrac{24 \; \text{hr}}{1 \; \text{day}} \times \dfrac{3600 \; \text{esc}}{1 \; \text{hour}} =2,358,720\; \text{sec}\nonumber \]
Підставляємо всі дані в Equation\ ref {Eq30} і вирішуємо для\(a\):
\[\begin{align*} (2,358,720sec)^2 = \dfrac{4\pi^2a^3}{\left( 6.67\times 10^{-11} \frac{m}{\text{kg}\times \text{sec}^2}\right) (7.35\times 10^{22}\text{kg} + 5.97 \times 10^{24}\text{kg})} \\ 5.563 \times 10^{12} = \dfrac{ 4\pi^2a^3}{(6.67 \times 10^{-11}\text{m}^3)(6.04 \times 10^{24})} \\ (5.563 \times 10^{12})(6.67 \times 10^{-11} \text{m}^3)(6.04 \times 10^{24}) = 4\pi^2 a^3 \\ a^3 = \dfrac{2.241 \times 10^{27}}{4\pi^2}\text{m}^3 \\ a = 3.84 \times 10^8 \text{m} \\ \approx 384,000 \,\text{km}. \end{align*}\]
Аналіз
За даними solarsystem.nasa.gov, фактична середня відстань від Місяця до Землі становить 384 400 км. Це обчислюється за допомогою відбивачів, залишених на Місяці астронавтами «Аполлона» ще в 1960-х роках.
Титан - найбільша Місяць Сатурна. Маса Титану приблизно\(1.35 \times 10^{23} kg\). Маса Сатурна становить приблизно\( 5.68 \times 10^{26}\) кг. Титану потрібно приблизно 16 днів на орбіті Сатурна. Використовуйте цю інформацію разом із загальною постійною гравітації\(G=6.67×10^{−11} \text{m}/\text{kg} \cdot \text{sec}^2\) для оцінки відстані від Титана до Сатурна.
- Підказка
-
Переконайтеся, що ваші одиниці згодні, а потім використовуйте Equation\ ref {Eq30}.
- Відповідь
-
\[a\approx 1.224 \times 10^9 \text{m}= 1,224,000 \text{km} \nonumber \]
Тепер повернемося до відкривачки глави, де обговорюється рух комети Галлея навколо Сонця. Перший закон Кеплера стверджує, що комета Галлея слідує еліптичним шляхом навколо Сонця, з Сонцем як одним фокусом еліпса. Період комети Галлея становить приблизно 76,1 року, залежно від того, наскільки тісно вона проходить повз Юпітера і Сатурна, коли проходить через зовнішню Сонячну систему. Давайте використовувати\(T=76.1\) роки. Яка середня відстань комети Галлея від Сонця?

Рішення
Використовуючи рівняння\(T^2=D^3\) с\(T=76.1\)\(D^3=5791.21\), отримаємо, так\(D\approx 17.96\) А.У. це виходить приблизно\(1.67\times 10^9\) mi.
Задати природне запитання: Які максимальні (афелії) та мінімальні (перигелії) відстані від комети Галлея до Сонця? Ексцентриситет орбіти комети Галлея дорівнює 0,967 (Джерело: http://nssdc.gsfc.nasa.gov/planetary...cometfact.html). Нагадаємо, що формула ексцентриситету еліпса така\(e=c/a\), де a - довжина великої півосі, а c - відстань від центру до будь-якого фокусу. Отже,\(0.967=c/17.96\) і\(c\approx 17.37\) А.У. віднімання цього з a дає перигелійну відстань\(p=a−c=17.96−17.37=0.59\) А.У., Згідно з даними Національного центру даних космічної науки (Джерело: http://nssdc.gsfc.nasa.gov/planetary...cometfact.html), перигелійна відстань для комети Галлея становить 0,587 А.У. для обчислення афеліонної відстані додаємо
\[ P=a+c=17.96+17.37=35.33 \; \text{A.U.} \nonumber \]
Це приблизно\(3.3\times 10^9\) милі. Середня відстань від Плутона до Сонця становить 39,5 А.У. (Джерело: http://www.oarval.org/furthest.htm), тому здавалося б, що комета Галлея залишається якраз в межах орбіти Плутона.
Як швидко гоночний автомобіль може подорожувати по круговому повороту без занесення і удару об стіну? Відповідь може залежати від декількох факторів:
- Вага автомобіля;
- Тертя між шинами і дорогою;
- Радіус кола;
- «Крутизна» повороту.
У цьому проекті ми досліджуємо це питання для гоночних автомобілів NASCAR на Bristol Motor Speedway в Теннессі. Перш ніж розглядати цей трек зокрема, ми використовуємо векторні функції для розробки математики та фізики, необхідних для відповіді на такі запитання.
Автомобіль маси\(m\) рухається з постійною кутовою швидкістю\(\omega\) навколо кругової кривої радіуса\(R\) (рис.\(\PageIndex{9}\)). Крива викривлена під кутом\(\theta\). Якщо висота автомобіля від землі дорівнює\(h\), то положення автомобіля на час\(t\) задається функцією\(\vecs r(t)=< R\cos(\omega t),R\sin(\omega t),h>\).

- Знайдіть\(\vecs{v}(t)\) швидкісну функцію автомобіля. Показати, що\(\vecs{v}\) є дотичною до кругової кривої. Це означає, що, не маючи сили тримати машину на кривій, автомобіль буде відстрілювати з нього.
- Покажіть, що швидкість автомобіля є\(\omega R\). Використовуйте це, щоб показати це\((2\pi 4)/\|\vecs{v}\|=(2\pi)/\omega \).
- Знайдіть прискорення\(\vecs{a}\). Покажіть, що цей вектор вказує на центр кола і що\(\|\vecs{a}\|=R\omega ^2\).
- Сила, необхідна для здійснення цього кругового руху, називається доцентровою силою, і позначається вона\( \vecs{F}_{cent} \). Ця сила вказує на центр кола (не до землі). Покажіть, що\(\|\vecs{F}_{cent}\|=\left(m|\vecs{v}|^2 \right)/R\).
У міру руху автомобіля навколо кривої на неї діють три сили: сила тяжіння, сила, що чиниться дорогою (ця сила перпендикулярна землі), і сила тертя (рис.\(\PageIndex{10}\)). Оскільки описуючи силу тертя, що генерується шинами і дорогою, є складним, ми використовуємо стандартне наближення для сили тертя. Припустимо, що\(\vecs{f}=\mu \vecs{N}\) для деякої позитивної\(\mu \) константи. Константа\(\mu\) називається коефіцієнтом тертя.
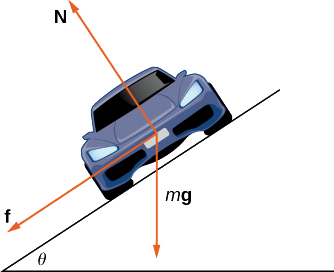
Нехай\(v_{max}\) позначимо максимальну швидкість, яку автомобіль може досягти через криву без занесення. Іншими словами,\(v_{max}\) це найшвидша швидкість, на якій автомобіль може орієнтуватися на повороті. Коли автомобіль їде з такою швидкістю, величина доцентрової сили дорівнює
\[\| \vecs{F}_{cent} \| = \dfrac{m(v_{max})^2}{R}. \nonumber \]
Наступні три питання стосуються розробки формули, яка пов'язує швидкість\(v_{max}\) з банківським кутом\(\theta\).
- Покажіть, що\(\vecs{N} \cos\theta=m\vecs g+\vecs{f} \sin\theta\). Зробіть висновок про це\(\vecs{N}=(m\vecs g)/(\cos\theta−\mu \sin\theta)\).
- Доцентрова сила - це сума сил в горизонтальному напрямку, так як доцентрова сила вказує на центр кругової кривої. Покажіть, що
\[\vecs{F}_{cent}=\vecs{N} \sin\theta+\vecs{f}\cos\theta. \nonumber \]
Зробіть висновок, що\[\vecs{F}_{cent}=\dfrac{\sin\theta+\mu \cos\theta}{cos\theta−\mu \sin\theta} m\vecs g. \nonumber \]
- Покажіть, що\((v_{\text{max}})^2=((\sin\theta+\mu\ cos\theta)/(\cos\theta−\mu \sin\theta))gR\). Зробіть висновок, що максимальна швидкість фактично не залежить від маси автомобіля.
Тепер, коли у нас є формула, що стосується максимальної швидкості автомобіля та банківського кута, ми можемо відповісти на запитання, подібні до того, що було поставлено на початку проекту.
Брістоль Motor Speedway є NASCAR шорт-трек в Брістолі, штат Теннессі. Доріжка має приблизну форму, показану на малюнку\(\PageIndex{11}\). Кожен кінець траси приблизно напівкруглий, тому, коли автомобілі роблять повороти, вони рухаються по приблизно круговій кривій. Якщо автомобіль проходить внутрішню колію і рухається по нижній частині повороту 1, автомобіль рухається півколом радіусом приблизно 211 футів з кутом нахилу 24°. Якщо автомобіль вирішує зайняти зовнішню колію і рухається по вершині повороту 1, то автомобіль їде по півколу з кутом нахилу 28°. (Доріжка має змінний кут нахилу.)

Коефіцієнт тертя для нормальної шини в сухих умовах становить приблизно 0,7. Тому припускаємо, що коефіцієнт для шини NASCAR в сухих умовах становить приблизно 0,98.
Перш ніж відповісти на наступні питання, зверніть увагу, що простіше зробити обчислення з точки зору футів і секунд, а потім конвертувати відповіді на милі на годину як завершальний крок.
- У сухих умовах, як швидко автомобіль може проїхати через нижню частину повороту без занесення?
- У сухих умовах, як швидко автомобіль може проїхати через верхню частину повороту без занесення?
- У вологих умовах коефіцієнт тертя може стати аж 0,1. Якщо це так, як швидко автомобіль може проїхати через нижню частину повороту без занесення?
- Припустимо, виміряна швидкість автомобіля, що йде по зовнішньому краю повороту, становить 105 км/год. Оцініть коефіцієнт тертя для шин автомобіля.
Ключові концепції
- Якщо\(\vecs{r}(t)\) представляє положення об'єкта в момент t, то\(\vecs{r}'(t)\) представляє швидкість і\(\vecs{r}′′(t)\) являє собою прискорення об'єкта в час t Величина вектора швидкості - швидкість.
- Вектор прискорення завжди вказує на увігнуту сторону кривої, визначеної\(\vecs{r}(t)\). Тангенціальна і нормальна складові прискорення\(a_\vecs{T}\) і\(a_\vecs{N}\) є проекціями вектора прискорення на одиничний тангенс і одиничний нормальний вектори на криву.
- Три закони руху планет Кеплера описують рух об'єктів на орбіті навколо Сонця. Його третій закон може бути змінений для опису руху об'єктів на орбіті навколо інших небесних об'єктів, а також.
- Ньютон зміг використати свій закон всесвітнього тяжіння у поєднанні зі своїм другим законом руху та числення, щоб довести три закони Кеплера.
Ключові рівняння
- Швидкість\[\vecs{v}(t)=\vecs{r}′(t) \nonumber \]
- Прискорення\[\vecs{a}(t)=\vecs{v}′(t)=\vecs{r}′′(t) \nonumber \]
- Швидкість\[v(t)=||\vecs{v}(t)||=||\vecs{r}′(t)||=\dfrac{ds}{dt} \nonumber \]
- Тангенціальна складова прискорення\[a_{\vecs{T}} =\vecs{a}\cdot \vecs{T}=\dfrac{\vecs{v}\cdot \vecs{a}}{||\vecs v||} \nonumber \]
- Нормальна складова прискорення\[a_{\vecs{N}}=\vecs{a}\cdot \vecs{N} = \dfrac{|| \vecs{v} \times \vecs{a} ||}{||\vecs{v}||} = \sqrt{||\vecs{a}||^2 - a_{\vecs{T}}} \nonumber \]
Глосарій
- вектор прискорення
- друга похідна вектора положення
- Закони Кеплера руху планет
- три закони, що регулюють рух планет, астероїдів і комет на орбіті навколо Сонця
- нормальна складова прискорення
- коефіцієнт одиничного вектора нормалі,\(\vecs N\) коли вектор прискорення записується як лінійна комбінація\(\vecs T\) і\(\vecs N\)
- рух снаряда
- рух об'єкта з початковою швидкістю, але ніякої сили, що діє на нього, крім сили тяжіння
- тангенціальна складова прискорення
- коефіцієнт одиничного тангенса вектора,\(\vecs T\) коли вектор прискорення записується як лінійна комбінація\(\vecs T\) і\(\vecs N\)
- вектор швидкості
- похідна вектора положення
Автори та атрибуція
- Template:ContribOpenStaxCalc
- Edited by Paul Seeburger
Paul Seeburger added finding point \((1, 2)\) when \(t=1\) in Example \(\PageIndex{1}\).
He also created Figure \(\PageIndex{1}\).
