13.1: Векторно-значні функції та просторові криві
- Page ID
- 61650
- Запишіть загальне рівняння векторно-значної функції в компонентній формі та одинично-векторній формі.
- Розпізнати параметричні рівняння для просторової кривої.
- Опишіть форму спіралі і запишіть її рівняння.
- Визначте межу векторної функції.
Наше дослідження векторно-значних функцій поєднує ідеї з нашого попереднього вивчення однозмінного числення з нашим описом векторів у трьох вимірах з попередньої глави. У цьому розділі ми розширюємо поняття з попередніх глав, а також розглядаємо нові ідеї щодо кривих у тривимірному просторі. Ці визначення та теореми підтримують виклад матеріалу в іншій частині цієї глави, а також в інших розділах тексту.
Визначення векторно-значної функції
Нашим першим кроком у вивченні числення векторно-значних функцій є визначення того, що саме є векторно-значною функцією. Потім ми можемо подивитися на графіки векторних функцій і побачити, як вони визначають криві як у двох, так і в трьох вимірах.
Векторно-значна функція - це функція виду
\[\vecs r(t)=f(t)\,\hat{\mathbf{i}}+g(t)\,\hat{\mathbf{j}} \; \; \text{or} \; \;\vecs r(t)=f(t)\,\hat{\mathbf{i}}+g(t)\,\hat{\mathbf{j}}+h(t)\,\hat{\mathbf{k}}, \nonumber \]
де компонентні функції\(f\)\(g\), і\(h\), є дійсними функціями параметру\(t\). Векторно-значні функції також записуються у вигляді
\[\vecs r(t)=⟨f(t),\,g(t)⟩ \; \; \text{or} \; \; \vecs r(t)=⟨f(t),\,g(t),\,h(t)⟩. \nonumber \]
В обох випадках перша форма функції визначає двовимірну векторно-значну функцію; друга форма описує тривимірну векторно-значну функцію.
Параметр\(t\) може лежати між двома дійсними числами:\(a≤t≤b\). Інша можливість полягає в тому, що значення\(t\) може взяти на себе всі дійсні числа. Нарешті, самі функції компонента можуть мати обмеження домену, які примушують обмеження на значення\(t\). Ми часто використовуємо\(t\) як параметр, тому що\(t\) може представляти час.
Для кожної з наступних векторно-значних функцій оцінюйте\(\vecs r(0)\)\(\vecs r(\frac{\pi}{2})\), і\(\vecs r(\frac{2\pi}{3})\). Чи є у будь-якої з цих функцій обмеження домену?
- \(\vecs r(t)=4\cos t\,\hat{\mathbf{i}}+3\sin t\,\hat{\mathbf{j}}\)
- \(\vecs r(t)=3\tan t\,\hat{\mathbf{i}}+4 \sec t\,\hat{\mathbf{j}}+5t\,\hat{\mathbf{k}}\)
Рішення
- Щоб обчислити кожне з значень функції, підставляємо відповідне значення\(t\) у функцію:
\ почати {вирівнювати*}\ векс r (0)\; = 4\ cos (0)\ капелюх {\ mathbf {i}} +3\ sin (0)\ капелюх {\ mathbf {j}}\\ [4pt] =4\ капелюх {\ mathbf {я}} +0\ шапка {\ mathbf {j}} =4\ капелюх {\ mathbf {j}} bf {i}}\\ [4pt]\ vecs r\ ліворуч (\ frac {\ pi} {2}\ праворуч)\; = 4\ cos\ ліворуч (\ frac {π} {2}\ праворуч)\ капелюх {\ mathbf {i}} +3\ sin\ ліворуч (\ frac {π} {2}\ праворуч)\ капелюх {\ mathbf {j}}\\ [4pt] = 0\ капелюх {\ mathbf {i}} + 3\ капелюх {\ mathbf {j}} =3\ капелюх {\ mathbf {j}}\\ [4pt]\ vecs r\ ліворуч (\ frac {2\ pi} {3}\ pi} {3}\ pi} {3\ pi} {3\ pi} {\ mathbf {i}}} +3\ sin\ ліворуч (\ frac {2π} {3}\ право)\ капелюх {\ mathbf {j}}\\ [4pt] =4\ ліворуч (−\ tfrac {1} {2}\ праворуч)\ капелюх {\ mathbf {i}} +3\ ліворуч (\ tfrac {\ sqrt {3}} {2}\ праворуч)\ капелюх {\ mathbf {j}} =−2\ капелюх {\ mathbf {i}} +\ tfrac {3\ sqrt {3}} {2}\ hat {\ mathbf {j}}\ end {вирівнювати*}
Щоб визначити, чи має ця функція якісь обмеження домену, розглянемо функції компонента окремо. Перша функція компонента є,\(f(t)=4 \cos t\) а друга функція компонента є\(g(t)=3\sin t\). Жодна з цих функцій не має обмеження домену, тому домен\(\vecs r(t)=4\cos t\,\hat{\mathbf{i}}+3 \sin t \,\hat{\mathbf{j}}\) - це всі дійсні числа. - Щоб обчислити кожне зі значень функції, підставити відповідне значення t у функцію:\[\begin{align*}\vecs r(0) \; = 3\tan(0)\hat{\mathbf{i}}+4\sec(0) \hat{\mathbf{j}}+5(0) \hat{\mathbf{k}} \\[4pt] = 0\hat{\mathbf{i}}+4j+0 \hat{\mathbf{k}}=4 \hat{\mathbf{j}} \\[4pt] \vecs r\left(\frac{\pi}{2}\right) \; = 3\tan\left(\frac{\pi}{2}\right)\hat{\mathbf{i}}+4\sec\left(\frac{\pi}{2}\right) \hat{\mathbf{j}}+5\left(\frac{\pi}{2}\right) \hat{\mathbf{k}},\,\text{which does not exist} \\[4pt] \vecs r\left(\frac{2\pi}{3}\right) \; =3\tan\left(\frac{2 \pi}{3}\right)\hat{\mathbf{i}}+4\sec\left(\frac{2\pi}{3}\right) \hat{\mathbf{j}}+5\left(\frac{2\pi}{ 3}\right) \hat{\mathbf{k}} \\[4pt] =3(−\sqrt{3})\hat{\mathbf{i}}+4(−2)\hat{\mathbf{j}}+\frac{10π}{3} \hat{\mathbf{k}} \\[4pt] =(-3\sqrt{3})\hat{\mathbf{i}}−8\hat{\mathbf{j}}+\frac{10π}{3} \hat{\mathbf{k}}\end{align*}\] Щоб визначити, чи має ця функція якісь обмеження області, розглянемо функції компонента окремо. Перша функція компонента - це\(f(t)=3\tan t\) функція другого компонента\(g(t)=4\sec t\), а функція третього компонента -\(h(t)=5t\). Перші дві функції не визначені для непарних кратних\(\frac{\pi}{2}\), тому функція не визначена для непарних кратних\(\frac{\pi}{2}\). Тому\[\text{D}_{\vecs r}=\Big\{t\,|\,t≠ \frac{(2n+1)\pi}{2}\Big\},\nonumber \] де\(n\) - будь-яке ціле число.
Для векторно-значної функції оцінюють\(\vecs r(t)=(t^2−3t) \,\hat{\mathbf{i}}+(4t+1) \,\hat{\mathbf{j}}\)\(\vecs r(0),\, \vecs r(1)\), і\(\vecs r(−4)\). Чи має ця функція обмеження по домену?
- Підказка
-
Підставляємо відповідні значення\(t\) у функцію.
- Відповідь
-
\(\vecs r(0) = \hat{\mathbf{j}},\, \vecs r(1)=−2 \hat{\mathbf{i}}+5 \hat{\mathbf{j}},\, \vecs r(−4)=28 \hat{\mathbf{i}}−15 \hat{\mathbf{j}}\)
Домен всіх\(\vecs r(t)=(t^2−3t)\hat{\mathbf{i}}+(4t+1)\hat{\mathbf{j}}\) дійсних чисел.
Приклад\(\PageIndex{1}\) ілюструє важливе поняття. Домен векторно-значної функції складається з дійсних чисел. Доменом можуть бути всі дійсні числа або підмножина дійсних чисел. Діапазон векторно-значної функції складається з векторів. Кожне дійсне число в області векторно-значної функції зіставляється або з дво- або тривимірним вектором.
Графічні векторні функції
Нагадаємо, що плоский вектор складається з двох величин: напрямку і величини. З огляду на будь-яку точку на площині (початкова точка), якщо ми рухаємося в певному напрямку на певну відстань, ми приходимо до другої точки. Це являє собою кінцеву точку вектора. Обчислюємо складові вектора, віднімаючи координати початкової точки з координат кінцевої точки.
Вектор вважається в стандартному положенні, якщо початкова точка розташована біля початку. При графіку векторної функції ми зазвичай графуємо вектори в області функції в стандартній позиції, тому що це гарантує унікальність графа. Ця угода застосовується і до графіків тривимірних векторно-значних функцій. Графік векторно-значної функції форми
\[\vecs r(t)=f(t)\, \hat{\mathbf{i}}+g(t)\,\hat{\mathbf{j}} \nonumber \]
складається з безлічі всіх точок\((f(t),\,g(t))\), а шлях, який він простежує, називається плоскою кривою. Графік векторно-значної функції форми
\[\vecs r(t)=f(t) \,\hat{\mathbf{i}}+g(t) \,\hat{\mathbf{j}}+h(t) \,\hat{\mathbf{k}} \nonumber \]
складається з безлічі всіх точок\((f(t),\,g(t),\,h(t))\), а шлях, який він простежує, називається просторовою кривою. Будь-яке зображення плоської кривої або просторової кривої з використанням векторно-значної функції називається векторною параметризацією кривої.
Кожна плоска крива і крива простору має орієнтацію, позначену стрілками, намальованими на кривій, яка показує напрямок руху вздовж кривої при\(t\) збільшенні значення параметра.
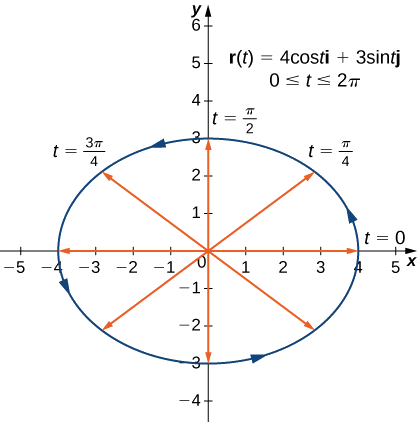
Створіть графік кожної з наступних векторно-значних функцій:
- Плоска крива представлена\(\vecs r(t)=4 \cos t \,\hat{\mathbf{i}}+3 \sin t \,\hat{\mathbf{j}}\),\(0≤t≤2\pi\)
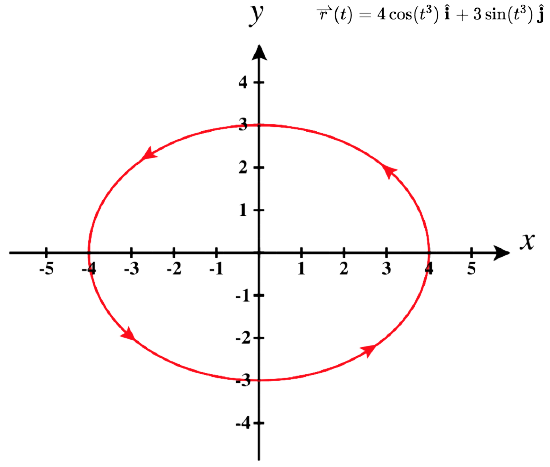
- Плоска крива представлена\(\vecs r(t)=4 \cos(t^3) \,\hat{\mathbf{i}}+3 \sin(t^3) \,\hat{\mathbf{j}}\),\(0≤t≤\sqrt[3]{2\pi}\)
- Космічна крива представлена\(\vecs r(t)=4 \cos t \,\hat{\mathbf{i}}+4 \sin t \,\hat{\mathbf{j}}+t \,\hat{\mathbf{k}}\),\(0≤t≤4\pi\)
Рішення
1. Як і на будь-якому графіку, починаємо з таблиці значень. Потім ми графуємо кожен з векторів у другому стовпці таблиці в стандартному положенні і з'єднуємо кінцеві точки кожного вектора, щоб сформувати криву (рис.\(\PageIndex{1}\)). Ця крива виявляється еліпсом з центром у початковій точці.
| \(t\) | \(\vecs r(t)\) | \(t\) | \(\vecs r(t)\) |
|---|---|---|---|
| \ (t\)» style="вертикальне вирівнювання: середина; ">\(0\) | \ (\ vecs r (t)\)» style="вертикальне вирівнювання: середина; ">\(4\hat{\mathbf{i}}\) | \ (t\)» style="вертикальне вирівнювання: середина; ">\(\pi\) | \ (\ vecs r (t)\)» style="вертикальне вирівнювання: середина; ">\(-4\hat{\mathbf{i}}\) |
| \ (t\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{\pi}{4}\) | \ (\ vecs r (t)\)» style="вертикальне вирівнювання: середина; ">\(2 \sqrt{2} \hat{\mathbf{i}} + \frac{3 \sqrt{2}}{2}\hat{\mathbf{j}}\) | \ (t\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{5\pi}{4}\) | \ (\ vecs r (t)\)» style="вертикальне вирівнювання: середина; ">\(-2 \sqrt{2} \hat{\mathbf{i}} - \frac{3 \sqrt{2}}{2}\hat{\mathbf{j}}\) |
| \ (t\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{\pi}{2}\) | \ (\ vecs r (t)\)» style="вертикальне вирівнювання: середина; ">\(\mathrm{3\hat{\mathbf{j}}}\) | \ (t\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{3\pi}{2}\) | \ (\ vecs r (t)\)» style="вертикальне вирівнювання: середина; ">\(\mathrm{-3\hat{\mathbf{j}}}\) |
| \ (t\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{3\pi}{4}\) | \ (\ vecs r (t)\)» style="вертикальне вирівнювання: середина; ">\( -2 \sqrt{2} \hat{\mathbf{i}} + \frac{3 \sqrt{2}}{2}\hat{\mathbf{j}}\) | \ (t\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{7\pi}{4}\) | \ (\ vecs r (t)\)» style="вертикальне вирівнювання: середина; ">\( 2 \sqrt{2} \hat{\mathbf{i}} - \frac{3 \sqrt{2}}{2}\hat{\mathbf{j}}\) |
| \ (t\)» style="вертикальне вирівнювання: середина; ">\(2\pi\) | \ (\ vecs r (t)\)» style="вертикальне вирівнювання: середина; ">\(4\hat{\mathbf{i}}\) | \ (t\)» style="вертикальне вирівнювання: середина; "> | \ (\ vecs r (t)\)» style="вертикальне вирівнювання: середина; "> |
2. Таблиця значень для\(\vecs r(t)=4 \cos(t^3) \,\hat{\mathbf{i}}+3 \sin(t^3) \,\hat{\mathbf{j}}\), виглядає\(0≤t≤\sqrt[3]{2\pi}\) наступним чином:
| \(t\) | \(\vecs r(t)\) | \(t\) | \(\vecs r(t)\) |
|---|---|---|---|
| \ (t\)» style="вертикальне вирівнювання: середина; ">\(0\) | \ (\ vecs r (t)\)» style="вертикальне вирівнювання: середина; ">\(\mathrm{4\hat{\mathbf{i}}}\) | \ (t\)» style="вертикальне вирівнювання: середина; ">\(\displaystyle\sqrt[3]{\pi}\) | \ (\ vecs r (t)\)» style="вертикальне вирівнювання: середина; ">\(\mathrm{-4\hat{\mathbf{i}}}\) |
| \ (t\)» style="вертикальне вирівнювання: середина; ">\(\displaystyle \sqrt[3]{\dfrac{\pi}{4}}\) | \ (\ vecs r (t)\)» style="вертикальне вирівнювання: середина; ">\(\mathrm{ 2 \sqrt{2} \hat{\mathbf{i}} + \frac{3 \sqrt{2}}{2}\hat{\mathbf{j}}}\) | \ (t\)» style="вертикальне вирівнювання: середина; ">\(\displaystyle \sqrt[3]{\dfrac{5\pi}{4}}\) | \ (\ vecs r (t)\)» style="вертикальне вирівнювання: середина; ">\(\mathrm{ -2 \sqrt{2} \hat{\mathbf{i}} - \frac{3 \sqrt{2}}{2}\hat{\mathbf{j}}}\) |
| \ (t\)» style="вертикальне вирівнювання: середина; ">\(\displaystyle \sqrt[3]{\dfrac{\pi}{2}}\) | \ (\ vecs r (t)\)» style="вертикальне вирівнювання: середина; ">\(\mathrm{3\hat{\mathbf{j}}}\) | \ (t\)» style="вертикальне вирівнювання: середина; ">\(\displaystyle \sqrt[3]{\dfrac{3\pi}{2}}\) | \ (\ vecs r (t)\)» style="вертикальне вирівнювання: середина; ">\(\mathrm{-3\hat{\mathbf{j}}}\) |
| \ (t\)» style="вертикальне вирівнювання: середина; ">\(\displaystyle \sqrt[3]{\dfrac{3\pi}{4}}\) | \ (\ vecs r (t)\)» style="вертикальне вирівнювання: середина; ">\(\mathrm{ -2 \sqrt{2} \hat{\mathbf{i}} + \frac{3 \sqrt{2}}{2}\hat{\mathbf{j}}}\) | \ (t\)» style="вертикальне вирівнювання: середина; ">\(\displaystyle \sqrt[3]{\dfrac{7\pi}{4}}\) | \ (\ vecs r (t)\)» style="вертикальне вирівнювання: середина; ">\(\mathrm{ 2 \sqrt{2} \hat{\mathbf{i}} - \frac{3 \sqrt{2}}{2}\hat{\mathbf{j}}}\) |
| \ (t\)» style="вертикальне вирівнювання: середина; ">\( \displaystyle\sqrt[3]{2\pi}\) | \ (\ vecs r (t)\)» style="вертикальне вирівнювання: середина; ">\(\mathrm{4\hat{\mathbf{i}}}\) | \ (t\)» style="вертикальне вирівнювання: середина; "> | \ (\ vecs r (t)\)» style="вертикальне вирівнювання: середина; "> |
Графік цієї кривої також є еліпсом, центрованим у початковій точці.
3. Проходимо ту ж процедуру для тривимірної векторної функції.
| \(t\) | \(\vecs r(t)\) | \(t\) | \(\vecs r(t)\) |
|---|---|---|---|
| \ (t\)» style="вертикальне вирівнювання: середина; ">\(\mathrm{0}\) | \ (\ vecs r (t)\)» style="вертикальне вирівнювання: середина; ">\(\mathrm{4\hat{\mathbf{i}}}\) | \ (t\)» style="вертикальне вирівнювання: середина; ">\(\mathrm{\pi}\) | \ (\ vecs r (t)\)» style="вертикальне вирівнювання: середина; ">\(\mathrm{-4\hat{\mathbf{i}}}+ \pi \hat{\mathbf{k}}\) |
| \ (t\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{\pi}{4}\) | \ (\ vecs r (t)\)» style="вертикальне вирівнювання: середина; ">\(\mathrm{2 \sqrt{2} \hat{\mathbf{i}} + 2\sqrt{2} \hat{\mathbf{j}} + \frac{\pi}{4} \hat{\mathbf{k}}}\) | \ (t\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{5\pi}{4}\) | \ (\ vecs r (t)\)» style="вертикальне вирівнювання: середина; ">\(\mathrm{ -2 \sqrt{2} \hat{\mathbf{i}} - 2\sqrt{2} \hat{\mathbf{j}} + \frac{5\pi}{4} \hat{\mathbf{k}}}\) |
| \ (t\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{\pi}{2}\) | \ (\ vecs r (t)\)» style="вертикальне вирівнювання: середина; ">\(\mathrm{4\hat{\mathbf{j}} +\frac{\pi}{2} \hat{\mathbf{k}}}\) | \ (t\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{3\pi}{2}\) | \ (\ vecs r (t)\)» style="вертикальне вирівнювання: середина; ">\(\mathrm{-4\hat{\mathbf{j}} +\frac{3\pi}{2} \hat{\mathbf{k}}}\) |
| \ (t\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{3\pi}{4}\) | \ (\ vecs r (t)\)» style="вертикальне вирівнювання: середина; ">\(\mathrm{ -2 \sqrt{2} \hat{\mathbf{i}} + 2\sqrt{2} \hat{\mathbf{j}} + \frac{3\pi}{4} \hat{\mathbf{k}}}\) | \ (t\)» style="вертикальне вирівнювання: середина; ">\(\dfrac{7\pi}{4}\) | \ (\ vecs r (t)\)» style="вертикальне вирівнювання: середина; ">\(\mathrm{ 2 \sqrt{2} \hat{\mathbf{i}} - 2\sqrt{2} \hat{\mathbf{j}} + \frac{7\pi}{4} \hat{\mathbf{k}}}\) |
| \ (t\)» style="вертикальне вирівнювання: середина; ">\(\mathrm{2\pi}\) | \ (\ vecs r (t)\)» style="вертикальне вирівнювання: середина; ">\(\mathrm{4\hat{\mathbf{j}} + 2\pi \hat{\mathbf{k}}}\) | \ (t\)» style="вертикальне вирівнювання: середина; "> | \ (\ vecs r (t)\)» style="вертикальне вирівнювання: середина; "> |
Значення потім повторюються самі, за винятком того, що\(\hat{\mathbf{k}}\) коефіцієнт завжди збільшується (\(\PageIndex{3}\)). Ця крива називається спіраллю. Зверніть увагу, що якщо\(\hat{\mathbf{k}}\) компонент усувається, то функція стає\(\vecs r(t)=4\cos t \hat{\mathbf{i}}+ 4\sin t \hat{\mathbf{j}}\), яка є окружністю радіуса 4 з центром у початку.

Ви можете помітити, що графіки в частинах. і б. ідентичні. Це відбувається тому, що функція, що описує криву b, є так званою репараметризацією функції, що описує криву a. Фактично, будь-яка крива має нескінченну кількість перепараметризацій; наприклад, ми можемо замінити на будь-яку\(t\) з\(2t\) трьох попередніх кривих без зміни форми крива. Інтервал, протягом\(t\) якого визначено, може змінитися, але це все. Ми повернемося до цієї ідеї пізніше в цьому розділі, коли ми вивчаємо параметризацію довжини дуги. Як уже згадувалося, назва форми кривої графіка в\(\PageIndex{3}\) - спіраль. Крива нагадує пружину, з круглим перетином дивиться вниз уздовж\(z\) -осі. Можна, щоб спіраль була еліптичною в поперечному перерізі, а також. Наприклад, векторно-значна функція\(\vecs r(t)=4 \cos t \,\hat{\mathbf{i}}+3 \sin t \,\hat{\mathbf{j}}+t \,\hat{\mathbf{k}}\) описує еліптичну спіраль. Проекція цієї спіралі в\(xy\) -площину є еліпсом. Нарешті, стрілки на графіку цієї спіралі вказують орієнтацію кривої по\(t\) ходу руху від\(0\) до\(4π\).
Створіть графік векторно-значної функції\(\vecs r(t)=(t^2−1)\hat{\mathbf{i}}+(2t−3) \hat{\mathbf{j}}\),\(0≤t≤3\).
- Підказка
-
Почніть зі створення таблиці значень, а потім графуйте вектори для кожного значення\(t\).
- Відповідь
-
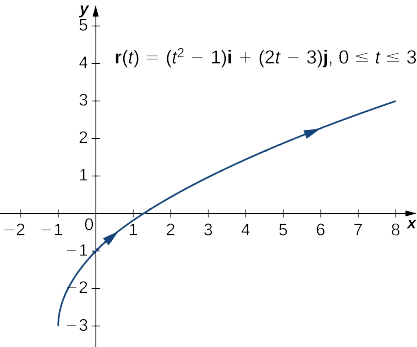
На цьому етапі ви можете помітити подібність між векторно-значними функціями та параметризованими кривими. Дійсно, з урахуванням векторно-значної функції\(\vecs r(t)=f(t)\,\hat{\mathbf{i}}+g(t)\,\hat{\mathbf{j}}\) ми можемо визначити\(x=f(t)\) і\(y=g(t)\). Якщо існує обмеження на значення\(t\) (наприклад,\(t\) обмежується інтервалом\([a,b]\) для деяких констант)\(a<b\), то це обмеження накладається на параметр. Потім графік параметризованої функції буде узгоджуватися з графіком векторно-значної функції, за винятком того, що векторно-значний граф буде представляти вектори, а не точки. Оскільки ми можемо параметризувати криву, визначену функцією\(y=f(x)\), можна також представляти довільну плоску криву векторною функцією.
Межі та неперервність векторно-значної функції
Тепер ми розглянемо межу векторної функції. Це важливо розуміти для вивчення числення векторно-значних функцій.
Векторно-значна функція\(\vecs r\) наближається до межі\(\vecs L\) як\(t\) підходи\(a\), написані
\[\lim \limits_{t \to a} \vecs r(t) = \vecs L, \nonumber \]
за умови
\[\lim \limits_{t \to a} \big\| \vecs r(t) - \vecs L \big\| = 0. \nonumber \]
Це суворе визначення межі векторно-значної функції. На практиці ми використовуємо наступну теорему:
Дозволяти\(f\)\(g\), і\(h\) бути функції\(t\). Тоді межа векторно-значної функції\(\vecs r(t)=f(t) \hat{\mathbf{i}}+g(t) \hat{\mathbf{j}}\) при наближенні t до a задається
\[\lim \limits_{t \to a} \vecs r(t) = [\lim \limits_{t \to a} f(t)] \hat{\mathbf{i}} + [\lim \limits_{t \to a} g(t)] \hat{\mathbf{j}} , \label{Th1} \]
передбачені ліміти\(\lim \limits_{t \to a} f(t)\) і\(\lim \limits_{t \to a} g(t)\) існують.
Аналогічно межа векторно-значної функції\(\vecs r(t)=f(t) \hat{\mathbf{i}}+g(t) \hat{\mathbf{j}}+h(t) \hat{\mathbf{k}}\) як\(t\) підходів\(a\) задається
\[\lim \limits_{t \to a} \vecs r(t) = [\lim \limits_{t \to a} f(t)] \hat{\mathbf{i}} + [\lim \limits_{t \to a} g(t)] \hat{\mathbf{j}} +[\lim \limits_{t \to a} h(t)] \hat{\mathbf{k}} , \label{Th2} \]
передбачені ліміти\(\lim \limits_{t \to a} f(t)\),\(\lim \limits_{t \to a} g(t)\) і\(\lim \limits_{t \to a} h(t)\) існують.
У наступному прикладі ми покажемо, як обчислити межу векторної функції.
Для кожної з наступних векторних функцій обчислити\(\lim \limits_{t \to 3}\vecs r(t)\) для
- \(\vecs r(t)=(t^2−3t+4) \hat{\mathbf{i}}+(4t+3)\hat{\mathbf{j}}\)
- \(\vecs r(t)=\frac{2t−4}{t+1}\hat{\mathbf{i}}+\frac{t}{t^2+1} \hat{\mathbf{j}}+(4t−3) \hat{\mathbf{k}}\)
Рішення
- Використовуйте Equation\ ref {Th1} і підставляйте значення\(t=3\) у два складові вирази:
\[ \begin{align*} \lim \limits_{t \to 3} \vecs r(t) \; = \lim \limits_{t \to 3} \left[(t^2−3t+4) \hat{\mathbf{i}} + (4t+3) \hat{\mathbf{j}}\right] \\[4pt] = \left[\lim \limits_{t \to 3} (t^2−3t+4)\right]\hat{\mathbf{i}}+\left[\lim \limits_{t \to 3} (4t+3)\right] \hat{\mathbf{j}} \\[4pt] = 4 \hat{\mathbf{i}}+15 \hat{\mathbf{j}} \end{align*}\]
- Використовуйте Equation\ ref {Th2} і підставляйте значення\(t=3\) у три складові вирази:
\[ \begin{align*} \lim \limits_{t \to 3} \vecs r(t) \; = \lim \limits_{t \to 3}\left(\dfrac{2t−4}{t+1}\hat{\mathbf{i}}+\dfrac{t}{t^2+1}\hat{\mathbf{j}}+(4t−3) \hat{\mathbf{k}}\right) \\[4pt] = \left[\lim \limits_{t \to 3} \left(\dfrac{2t−4}{t+1}\right)\right]\hat{\mathbf{i}}+\left[\lim \limits_{t \to 3} \left(\dfrac{t}{t^2+1}\right)\right] \hat{\mathbf{j}} +\left[\lim \limits_{t \to 3} (4t−3)\right] \hat{\mathbf{k}} \\[4pt] = \tfrac{1}{2} \hat{\mathbf{i}}+\tfrac{3}{10}\hat{\mathbf{j}}+9 \hat{\mathbf{k}} \end{align*}\]
Розрахувати\(\lim \limits_{t \to 2} \vecs r(t)\) для функції\(\vecs r(t) = \sqrt{t^2 + 3t - 1}\,\hat{\mathbf{i}}−(4t-3)\hat{\mathbf{j}}− \sin \frac{(t+1)\pi}{2}\hat{\mathbf{k}}\)
- Підказка
-
Використовуйте рівняння\ ref {Th2} з попередньої теореми.
- Відповідь
-
\[\lim \limits_{t \to 2} \vecs r(t) = 3\hat{\mathbf{i}}−5\hat{\mathbf{j}}+\hat{\mathbf{k}} \nonumber \]
Тепер, коли ми знаємо, як обчислити межу векторної функції, ми можемо визначити неперервність у точці для такої функції.
Дозволяти\(f\)\(g\), і\(h\) бути функції\(t\). Потім векторно-значна функція\(\vecs r(t)=f(t) \hat{\mathbf{i}}+g(t)\hat{\mathbf{j}}\) є безперервною в точці,\(t=a\) якщо дотримуються наступних трьох умов:
- \(\vecs r(a)\)існує
- \(\lim \limits_{t \to a} \vecs r(t)\)існує
- \(\lim \limits_{t \to a} \vecs r(t) = \vecs r(a)\)
Аналогічно, векторно-значна функція\(\vecs r(t)=f(t) \hat{\mathbf{i}}+g(t)\hat{\mathbf{j}}+h(t)\hat{\mathbf{k}}\) є неперервною в точці,\(t=a\) якщо дотримуються наступних трьох умов:
- \(\vecs r(a)\)існує
- \(\lim \limits_{t \to a} \vecs r(t)\)існує
- \(\lim \limits_{t \to a} \vecs r(t) = \vecs r(a)\)
Резюме
- Векторно-значна функція - це функція виду\(\vecs r(t)=f(t) \hat{\mathbf{i}}+ g(t) \hat{\mathbf{j}}\) або\(\vecs r(t)=f(t) \hat{\mathbf{i}}+g(t) \hat{\mathbf{j}}+h(t) \hat{\mathbf{k}}\), де функції компонента\(f\)\(g\), і\(h\) є дійсними функціями параметру\(t\).
- Графік векторнозначної функції виду\(\vecs r(t)=f(t) \hat{\mathbf{i}}+g(t) \hat{\mathbf{j}}\) називається плоскою кривою. Графік векторнозначної функції виду\(\vecs r(t)=f(t)\hat{\mathbf{i}}+g(t)\hat{\mathbf{j}}+h(t) \hat{\mathbf{k}}\) називається просторовою кривою.
- Довільну плоску криву можна зобразити векторно-значною функцією.
- Для обчислення межі векторно-значної функції обчислити межі компонентних функцій окремо.
Ключові рівняння
- Векторно-значна функція
\(\vecs r(t)=f(t) \hat{\mathbf{i}}+g(t) \hat{\mathbf{j}}\) or\(\vecs r(t)=f(t) \hat{\mathbf{i}}+g(t) \hat{\mathbf{j}}+h(t) \hat{\mathbf{k}}\), або\(\vecs r(t)=⟨f(t),g(t)⟩\) або\(\vecs r(t)=⟨f(t),g(t),h(t)⟩\) - Межа векторної функції
\(\lim \limits_{t \to a} \vecs r(t) = [\lim \limits_{t \to a} f(t)] \hat{\mathbf{i}} + [\lim \limits_{t \to a} g(t)] \hat{\mathbf{j}}\) або\(\lim \limits_{t \to a} \vecs r(t) = [\lim \limits_{t \to a} f(t)] \hat{\mathbf{i}} + [\lim \limits_{t \to a} g(t)] \hat{\mathbf{j}} + [\lim \limits_{t \to a} h(t)] \hat{\mathbf{k}}\)
Глосарій
- компонентні функції
- компонентними функціями векторно-значної функції\(\vecs r(t)=f(t)\hat{\mathbf{i}}+g(t)\hat{\mathbf{j}}\) є\(f(t)\) і\(g(t)\), а компонентними функціями векторно-значної функції\(\vecs r(t)=f(t)\hat{\mathbf{i}}+g(t)\hat{\mathbf{j}}+h(t)\hat{\mathbf{k}}\) є\(f(t)\),\(g(t)\) і\(h(t)\)
- спіраль
- тривимірна крива у формі спіралі
- межа векторно-значної функції
- векторно-значна функція\(\vecs r(t)\) має межу,\(\vecs L\) як\(t\) наближається,\(a\) якщо\(\lim \limits{t \to a} \left| \vecs r(t) - \vecs L \right| = 0\)
- плоска крива
- множина впорядкованих пар\((f(t),g(t))\) разом з їх визначальними параметричними рівняннями\(x=f(t)\) та\(y=g(t)\)
- репараметризація
- альтернативна параметризація заданої векторно-значної функції
- космічна крива
- множина впорядкованих трійок\((f(t),g(t),h(t))\) разом з їх визначальними параметричними рівняннями\(x=f(t)\),\(y=g(t)\) і\(z=h(t)\)
- векторна параметризація
- будь-яке представлення площини або просторової кривої з використанням векторної функції
- векторно-значна функція
- функція виду\(\vecs r(t)=f(t)\hat{\mathbf{i}}+g(t)\hat{\mathbf{j}}\) або\(\vecs r(t)=f(t)\hat{\mathbf{i}}+g(t)\hat{\mathbf{j}}+h(t)\hat{\mathbf{k}}\), де функціонує компонент\(f\)\(g\), і\(h\) є дійсними функціями параметру\(t\).
Дописувачі та атрибуція
- Template:ContribOpenStaxCalc
- Edited by Paul Seeburger (Monroe Community College)
