4.9: Хрестовий продукт

Результати

1. Обчислити перехресний добуток і коробковий добуток векторів в$\mathbb{R}^3$.

Нагадаємо, що крапковий добуток є одним з двох важливих добутків векторів. Другий тип добутку для векторів називається перехресним добутком. Важливо зазначити, що перехресний твір визначається лише в$\mathbb{R}^{3}.$ Спочатку ми обговорюємо геометричне значення, а потім дається опис з точки зору координат, обидва з яких важливі. Геометричний опис має важливе значення для розуміння застосувань фізики та геометрії, тоді як опис координат необхідний для обчислення перехресного добутку.

Розглянемо наступне визначення.

Визначення$\PageIndex{1}$: Right Hand System of Vectors

Три вектора,$\vec{u},\vec{v},\vec{w}$ утворюють систему правої руки, якщо коли ви витягнете пальці правої руки уздовж напрямку вектора$\vec{u}$ і закриваєте їх у напрямку$\vec{v}$, великий палець вказує приблизно в напрямку$\vec{w}$.

Приклад правші системи векторів дивіться на наступному малюнку.

Малюнок$\PageIndex{1}$

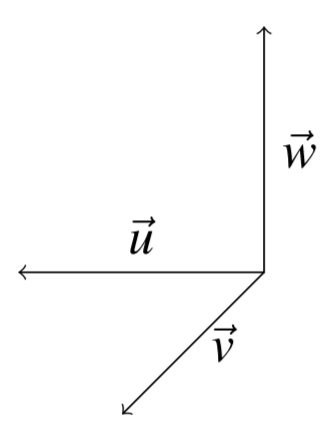
На цьому малюнку вектор$\vec{w}$ вказує вгору від площини, визначеної двома іншими векторами. Направте пальці правої руки уздовж$\vec{u}$, і зімніть їх у напрямку$\vec{v}$. Зверніть увагу, що якщо ви витягнете великий палець на правій руці, він вказує в сторону$\vec{w}$.

Ви повинні розглянути, як права система буде відрізнятися від системи лівої руки. Спробуйте використовувати ліву руку, і ви побачите, що вектор потрібно$\vec{w}$ буде вказувати в зворотному напрямку.

Зверніть увагу, що спеціальні вектори, завжди$\vec{i},\vec{j},\vec{k}$ будуть формувати праворучну систему. Якщо витягнути пальці правої руки уздовж$\vec{i}$ і зімкнути їх у напрямку$\vec{j}$, великий палець вказує в сторону$\vec{k}$.

Малюнок$\PageIndex{2}$

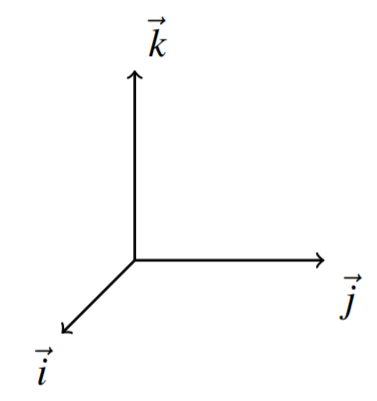
Далі наведено геометричний опис хрестового виробу. Нагадаємо, що крапковий добуток двох векторів призводить до скаляра. На відміну від цього, перехресний добуток призводить до вектора, оскільки твір дає напрямок, а також величину.

Визначення$\PageIndex{2}$: Geometric Definition of Cross Product

$\vec{u}$$\vec{v}$Дозволяти і бути два вектори в$\mathbb{R}^{3}.$ Тоді перехресний$\vec{u}\times \vec{v}$ добуток, записаний, визначається наступними двома правилами.

1. Його довжина - це $$\| \vec{u}\times \vec{v}\| =\| \vec{u}\| \| \vec{v}\| \sin \theta, \nonumber$$ місце$\theta$, де знаходиться включений кут між$\vec{u}$ і$\vec{v}$.
2. Вона перпендикулярна обох$\vec{u}$ і$\vec{v}$, тобто $$\left( \vec{u}\times \vec{v} \right) \cdot \vec{u}=0,$$ $$\left( \vec{u}\times \vec{v} \right) \cdot \vec{v}=0, \nonumber$$ і $$\vec{u},\vec{v},\vec{u}\times \vec{v} \nonumber$$ утворює систему правої руки.

Перехресний добуток спеціальних векторів виглядає$\vec{i}, \vec{j}, \vec{k}$ наступним чином. $$\begin{array}{cc} \vec{i}\times \vec{j}=\vec{k} & \vec{j}\times \vec{i}=-\vec{k} \\ \vec{k}\times \vec{i}=\vec{j} & \vec{i}\times \vec{k}=-\vec{j} \\ \vec{j}\times \vec{k}=\vec{i} & \vec{k}\times \vec{j}=-\vec{i} \end{array}\nonumber$$ З цією інформацією наступне дає координатний опис перехресного твір.

Нагадаємо, що вектор$\vec{u}= \left[ \begin{array}{ccc} u_1 & u_2 & u_3 \end{array} \right]^T$ можна записати в терміні$\vec{i}, \vec{j}, \vec{k}$ як$\vec{u}=u_{1}\vec{i}+u_{2}\vec{j}+u_{3}\vec{k}$.

Теорема$\PageIndex{1}$: Coordinate Description of Cross Product

$\vec{v}=v_{1}\vec{i}+v_{2}\vec{j}+v_{3}\vec{k}$Дозволяти$\vec{u}=u_{1}\vec{i}+u_{2}\vec{j}+u_{3}\vec{k}$ і бути двома векторами. Тоді

$$\begin{array}{c} \vec{u}\times \vec{v} =\left( u_{2}v_{3}-u_{3}v_{2}\right) \vec{i}-\left( u_{1}v_{3} - u_{3}v_{1}\right) \vec{j}+ \left( u_{1}v_{2}-u_{2}v_{1}\right) \vec{k} \label{crossprod1} \end{array}$$

Написання$\vec{u} \times \vec{v}$ звичайним способом, це дається

$$\vec{u} \times \vec{v} = \left[ \begin{array}{r} u_{2}v_{3}-u_{3}v_{2} \\ -(u_{1}v_{3}-u_{3}v_{1}) \\ u_{1}v_{2}-u_{2}v_{1} \end{array} \right]\nonumber$$

Ми зараз доводимо цю пропозицію.

Доказ

З наведеної вище таблиці і властивостей перехресного продукту перераховані, $$\begin{aligned} \vec{u} \times \vec{v} &= \left( u_{1}\vec{i}+u_{2}\vec{j}+u_{3}\vec{k}\right) \times \left( v_{1}\vec{i}+v_{2}\vec{j}+v_{3}\vec{k}\right) \\ &= u_{1}v_{2}\vec{i}\times \vec{j}+u_{1}v_{3}\vec{i}\times \vec{k}+u_{2}v_{1}\vec{j}\times \vec{i}+ u_{2}v_{3}\vec{j}\times \vec{k}+ +u_{3}v_{1}\vec{k}\times \vec{i}+u_{3}v_{2}\vec{k}\times \vec{j} \\ &=u_{1}v_{2}\vec{k}-u_{1}v_{3}\vec{j}-u_{2}v_{1}\vec{k}+u_{2}v_{3} \vec{i}+u_{3}v_{1}\vec{j}-u_{3}v_{2}\vec{i} \\ &=\left( u_{2}v_{3}-u_{3}v_{2}\right) \vec{i}+\left( u_{3}v_{1}-u_{1}v_{3}\right) \vec{j}+\left( u_{1}v_{2}-u_{2}v_{1}\right) \vec{k} \end{aligned}$$ $$\label{crossprod2}$$

Є ще один варіант$\eqref{crossprod1}$, який може бути легше запам'ятати. Ми можемо виразити перехресний добуток як визначник матриці наступним чином.

$$\vec{u}\times \vec{v} = \left\vert \begin{array}{ccc} \vec{i} & \vec{j} & \vec{k} \\ u_{1} & u_{2} & u_{3} \\ v_{1} & v_{2} & v_{3} \end{array} \right\vert \label{crossprod3}$$ Розширення детермінанта вздовж верхнього ряду дає $$\vec{i}\left( -1\right) ^{1+1}\left\vert \begin{array}{cc} u_{2} & u_{3} \\ v_{2} & v_{3} \end{array} \right\vert +\vec{j}\left( -1\right) ^{2+1}\left\vert \begin{array}{cc} u_{1} & u_{3} \\ v_{1} & v_{3} \end{array} \right\vert +\vec{k}\left( -1\right) ^{3+1}\left\vert \begin{array}{cc} u_{1} & u_{2} \\ v_{1} & v_{2} \end{array} \right\vert\nonumber$$ \

$$=\vec{i}\left\vert \begin{array}{cc} u_{2} & u_{3} \\ v_{2} & v_{3} \end{array} \right\vert -\vec{j}\left\vert \begin{array}{cc} u_{1} & u_{3} \\ v_{1} & v_{3} \end{array} \right\vert +\vec{k}\left\vert \begin{array}{cc} u_{1} & u_{2} \\ v_{1} & v_{2} \end{array} \right\vert\nonumber$$

Розширення цих детермінант призводить до $$\left( u_{2}v_{3}-u_{3}v_{2}\right) \vec{i}-\left( u_{1}v_{3}-u_{3}v_{1}\right) \vec{j}+\left( u_{1}v_{2}-u_{2}v_{1}\right) \vec{k} \nonumber$$ чого те ж саме, що і$\eqref{crossprod2}$.

Перехресне виріб задовольняє наступним властивостям.

Пропозиція$\PageIndex{1}$: Properties of the Cross Product

$\vec{u}, \vec{v}, \vec{w}$Дозволяти вектори в$\mathbb{R}^3$, і$k$ скалярний. Потім дотримуються наступні властивості перехресного виробу.

1. $\vec{u}\times \vec{v}= -\left( \vec{v}\times \vec{u}\right), \mbox{and} \; \vec{u}\times \vec{u}=\vec{0}$
2. $\left( k \vec{u}\right)\times \vec{v}= k \left( \vec{u}\times \vec{v}\right) =\vec{u}\times \left( k \vec{v}\right)$
3. $\vec{u}\times \left( \vec{v}+\vec{w}\right) =\vec{u}\times \vec{v}+\vec{u}\times \vec{w}$
4. $\left( \vec{v}+\vec{w}\right) \times \vec{u}=\vec{v} \times \vec{u}+\vec{w}\times \vec{u}$

Доказ

Формула$1.$ випливає відразу з визначення. Вектори$\vec{u}\times \vec{v}$ і$\vec{v}\times \vec{u}$ мають однакову величину,$\left\vert \vec{u}\right\vert \left\vert \vec{v}\right\vert \sin \theta ,$ а застосування правила правої руки показує, що вони мають протилежний напрямок.

Формула$2.$ доведена наступним чином. Якщо$k$ є невід'ємним скаляром, напрямок$\left( k \vec{u}\right) \times \vec{v}$ є таким же, як$\vec{u}\times \vec{v}, k \left( \vec{u}\times \vec{v}\right)$ і напрямок і$\vec{u}\times \left( k \vec{v}\right)$. Величина в$k$ рази величина$\vec{u}\times \vec{v}$ якої така ж, як і величина$k \left( \vec{u}\times \vec{v}\right)$ і$\vec{u}\times \left( k \vec{v}\right) .$ Використання цього дає рівність в$2$. У випадку, коли$k <0,$ все працює так само, крім векторів, всі вказують у зворотному напрямку, і ви повинні помножити на$\left\vert k \right\vert$ при порівнянні їх величини.

Розподільні$3.$ закони$4.$, і, набагато складніше встановити. Наразі достатньо помітити, що якщо ми знаємо, що$3.$ це правда,$4.$ слід. Таким чином, припускаючи$3.$, і використовуючи$1.$, $$\begin{aligned} \left( \vec{v}+\vec{w}\right) \times \vec{u}& =-\vec{u}\times \left( \vec{v}+\vec{w}\right) \\ & =-\left( \vec{u}\times \vec{v}+\vec{u}\times \vec{w}\right) \\ & =\vec{v}\times \vec{u}+\vec{w}\times \vec{u}\end{aligned}$$

Ми зараз розглянемо приклад того, як обчислити крос-добуток.

Приклад$\PageIndex{1}$: Find a Cross Product

Знайти$\vec{u} \times \vec{v}$ для наступних векторів

$$\vec{u} = \left[ \begin{array}{r} 1 \\ -1 \\ 2 \end{array} \right], \vec{v} = \left[ \begin{array}{r} 3 \\ -2 \\ 1 \end{array} \right]\nonumber$$

Рішення

Зауважте, що ми можемо писати$\vec{u}, \vec{v}$ в терміні спеціальних векторів$\vec{i}, \vec{j}, \vec{k}$ як

$$\begin{array}{c} \vec{u} = \vec{i}-\vec{j}+2\vec{k} \\ \vec{v} = 3\vec{i}-2\vec{j}+\vec{k} \end{array}\nonumber$$

Ми будемо використовувати рівняння, задане$\eqref{crossprod3}$ для обчислення перехресного добутку.

$$\vec{u} \times \vec{v} = \left\vert \begin{array}{rrr} \vec{i} & \vec{j} & \vec{k} \\ 1 & -1 & 2 \\ 3 & -2 & 1 \end{array} \right\vert =\left\vert \begin{array}{rr} -1 & 2 \\ -2 & 1 \end{array} \right\vert \vec{i}-\left\vert \begin{array}{rr} 1 & 2 \\ 3 & 1 \end{array} \right\vert \vec{j}+\left\vert \begin{array}{rr} 1 & -1 \\ 3 & -2 \end{array} \right\vert \vec{k}=3\vec{i}+5\vec{j}+\vec{k}\nonumber$$

Цей результат ми можемо записати звичайним способом, як $$\vec{u} \times \vec{v} = \left[ \begin{array}{r} 3 \\ 5 \\ 1 \end{array} \right]\nonumber$$

Важливим геометричним нанесенням поперечного виробу є наступне. Розмір поперечного твору$\| \vec{u}\times \vec{v}\|$, - це площа паралелограма, визначена$\vec{u}$ і$\vec{v}$, як показано на наступному малюнку.

Малюнок$\PageIndex{3}$

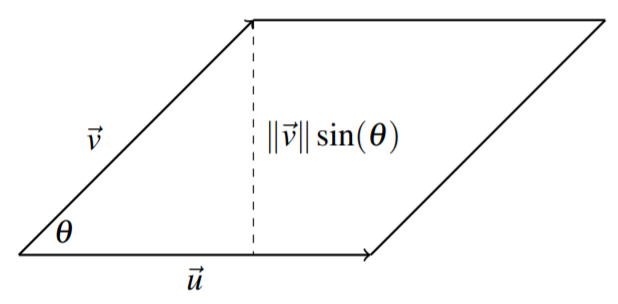
Розглянемо це поняття на наступному прикладі.

Приклад$\PageIndex{2}$: Area of a Parallelogram

Знайти площу паралелограма, визначену векторами$\vec{u}$ і$\vec{v}$ задану

$$\vec{u} = \left[ \begin{array}{r} 1 \\ -1 \\ 2 \end{array} \right], \vec{v} = \left[ \begin{array}{r} 3 \\ -2 \\ 1 \end{array} \right]\nonumber$$

Рішення

Зверніть увагу, що ці вектори такі ж, як ті, які наведені в прикладі$\PageIndex{1}$. Нагадаємо з геометричного опису перехресного добутку, що площа паралелограма є просто величиною$\vec{u} \times \vec{v}$. З прикладу$\PageIndex{1}$,$\vec{u} \times \vec{v} = 3\vec{i}+5\vec{j}+\vec{k}$. Ми також можемо написати це як

$$\vec{u} \times \vec{v} = \left[ \begin{array}{r} 3 \\ 5 \\ 1 \end{array} \right]\nonumber$$

Таким чином, площа паралелограма дорівнює

$$\| \vec{u} \times \vec{v} \| = \sqrt{(3)(3) + (5)(5) + (1)(1)} = \sqrt{9+25+1}=\sqrt{35}\nonumber$$

Ми також можемо використовувати це поняття, щоб знайти площу трикутника. Розглянемо наступний приклад.

Приклад$\PageIndex{3}$: Area of Triangle

Знайти площу трикутника, визначену точками$\left(1, 2, 3 \right) , \left( 0,2,5\right), \left( 5,1, 2 \right)$

Рішення

Цей трикутник виходить, з'єднавши три точки лініями. Вибираючи в$\left( 1,2,3\right)$ якості відправної точки, є два вектори зміщення,$\left[ \begin{array}{rrr} -1 & 0 & 2 \end{array} \right]^T$ і$\left[ \begin{array}{rrr} 4 & -1 & -1 \end{array} \right]^T$. Зверніть увагу, що якщо ми додамо будь-який з цих векторів до вектора позиції початкової точки, результатом є вектори положення двох інших точок. Тепер площа трикутника дорівнює половині площі паралелограма, визначеної$\left[ \begin{array}{rrr} -1 & 0 & 2 \end{array} \right]^T$ і Необхідний перехресний$\left[ \begin{array}{rrr} 4 & -1 & -1 \end{array} \right]^T.$ добуток задається

$$\left[ \begin{array}{r} -1 \\ 0 \\ 2 \end{array} \right] \times \left[ \begin{array}{r} 4 \\ -1 \\ -1 \end{array} \right] = \left[ \begin{array}{rrr} 2 & 7 & 1 \end{array} \right]\nonumber$$

Прийняття розміру цього вектора дає площу паралелограма, задану

$$\sqrt{(2)(2) + (7)(7) + (1)(1)} = \sqrt{4+49+1} = \sqrt{54}\nonumber$$ Звідси площа трикутника$\frac{1}{2}\sqrt{54}= \frac{3}{2}\sqrt{6}.$

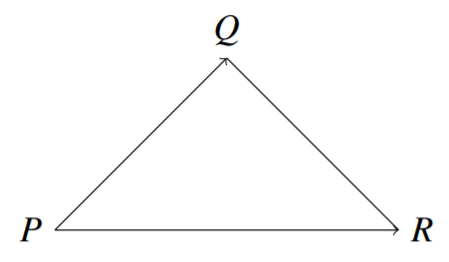
Загалом, якщо у вас три точки$\mathbb{R}^{3}, P,Q,R$, площа трикутника задається $$\frac{1}{2}\| \vec{PQ} \times \vec{PR} \|\nonumber$$

Нагадаємо, що$\vec{PQ}$ це вектор, що біжить з точки$P$ в точку$Q$.

Малюнок$\PageIndex{4}$

У наступному розділі ми досліджуємо ще одне застосування поперечного виробу.

Коробка продукту

Нагадаємо, що ми можемо використовувати перехресний добуток, щоб знайти площу паралелограма. Звідси випливає, що ми можемо використовувати перехресний твір разом з точковим добутком, щоб знайти об'єм паралелепіпеда. Почнемо з визначення.

Визначення$\PageIndex{3}$: Parallelepiped

Паралелепіпед визначається трьома векторами$\vec{u},\vec{v}$, і$\vec{w}$ складається з $$\left\{ r\vec{u}+s\vec{v}+t\vec{w}:r,s,t\in \left[ 0,1\right] \right\}\nonumber$$

Тобто, якщо вибрати три числа,$r,s,$ і$t$ кожне в$\left[ 0,1\right]$ формі,$r\vec{u}+s\vec{v}+t\vec{w}$ то збір всіх таких точок становить паралелепіпед, який визначається цими трьома векторами.

Нижче наведено приклад паралелепіпеда.

Малюнок$\PageIndex{5}$

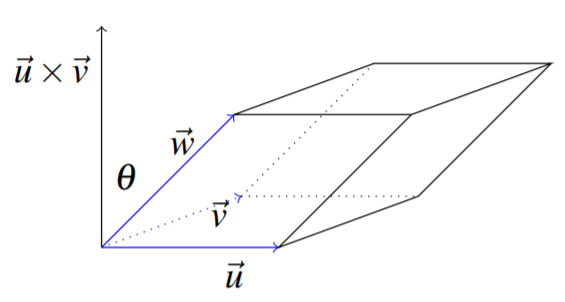
Зверніть увагу, що основою паралелепіпеда є паралелограм, що визначається векторами$\vec{u}$ і$\vec{v}$. Тому його площа дорівнює$\| \vec{u}\times \vec{v} \|$. Висота паралелепіпеда - це те,$\| \vec{w}\| \cos \theta$ де$\theta$ знаходиться кут, показаний на малюнку між$\vec{w}$ і$\vec{u}\times \vec{v}$. Обсяг цього паралелепіпеда - це площа підстави разів на висоту, яка є якраз $$\| \vec{u}\times \vec{v}\| \| \vec{w}\| \cos \theta = \left( \vec{u}\times\vec{v}\right) \cdot \vec{w}\nonumber$$ Цей вираз відомий як коробковий продукт і іноді пишеться так, як$\left[ \vec{u},\vec{v},\vec{w}\right] .$ Ви повинні розглянути, що станеться, якщо ви$\vec{v}$ поміняєте$\vec{u}$ з$\vec{w}$ або з $\vec{w}$. Ви можете побачити геометрично з малювання малюнків, що це просто вводить знак мінус. У будь-якому випадку коробковий добуток трьох векторів завжди дорівнює або об'єму паралелепіпеда, визначеному трьома векторами, або ще$-1$ раз цей об'єм.

Пропозиція$\PageIndex{2}$: The Box Product

$\vec{u}, \vec{v}, \vec{w}$Дозволяти три вектори в$\mathbb{R}^n$ які визначають паралелепіпед. Тоді обсяг паралелепіпеда - абсолютна величина коробчатого вироби, задана $$\left| \left(\vec{u}\times\vec{v}\right) \cdot \vec{w} \right|\nonumber$$

Розглянемо приклад цього поняття.

Приклад$\PageIndex{4}$: Volume of a Parallelepiped

Знайти обсяг паралелепіпеда, що визначається векторами

$$\vec{u} = \left[ \begin{array}{r} 1 \\ 2 \\ -5 \end{array} \right], \vec{v} = \left[ \begin{array}{r} 1 \\ 3 \\ -6 \end{array} \right], \vec{w} = \left[ \begin{array}{r} 3 \\ 2 \\ 3 \end{array} \right]\nonumber$$

Рішення

Відповідно до наведеного вище обговорення, виберіть будь-які два з цих векторів, візьміть перехресний добуток, а потім візьміть крапковий добуток цього з третім з цих векторів. Результатом буде або бажаний обсяг, або в$-1$ рази більший бажаний обсяг. Тому, взявши абсолютне значення результату, отримуємо обсяг.

Ми візьмемо перехресний твір$\vec{u}$ і$\vec{v}$. Це дається

$$\vec{u} \times \vec{v} = \left[ \begin{array}{r} 1 \\ 2 \\ -5 \end{array} \right] \times \left[ \begin{array}{r} 1 \\ 3 \\ -6 \end{array} \right]\nonumber$$ $$=\left\vert \begin{array}{rrr} \vec{i} & \vec{j} & \vec{k} \\ 1 & 2 & -5 \\ 1 & 3 & -6 \end{array} \right\vert = 3\vec{i}+\vec{j}+\vec{k} = \left[ \begin{array}{r} 3 \\ 1 \\ 1 \end{array} \right]\nonumber$$

Тепер візьмемо крапковий добуток цього вектора$\vec{w}$, з яким виходить $$\begin{aligned} (\vec{u} \times \vec{v}) \cdot \vec{w} &= \left[ \begin{array}{r} 3 \\ 1 \\ 1 \end{array} \right] \cdot \left[ \begin{array}{r} 3 \\ 2 \\ 3 \end{array} \right] \\ &=\left( 3\vec{i}+\vec{j}+\vec{k}\right) \cdot \left( 3\vec{i}+2\vec{j}+3\vec{k}\right) \\ &=9+2+3 \\ &=14\end{aligned}$$

Це показує обсяг цього паралелепіпеда в 14 кубічних одиниць.

Існує фундаментальне спостереження, яке походить безпосередньо з геометричних визначень перехресного добутку та точкового добутку.

Пропозиція$\PageIndex{3}$: Order of the Product

Дозволяти$\vec{u},\vec{v}$, і$\vec{w}$ бути вектори. Тоді$\left( \vec{u}\times \vec{v}\right) \cdot \vec{w}=\vec{u}\cdot \left( \vec{v}\times \vec{w} \right) .$

Доказ

Це випливає із спостереження, що або$\left( \vec{u}\times \vec{v}\right) \cdot \vec{w}$$\vec{u}\cdot \left( \vec{v}\times \vec{w}\right)$ обидва надають об'єм паралелепіпеда, або вони обидва дають в$-1$ рази більше обсягу.

Нагадаємо, що ми можемо виразити перехресний добуток як детермінанту тієї чи іншої матриці. Виходить, що те ж саме можна зробити і для коробчатого вироби. Припустимо, у вас є три вектори,$\vec{u}=\left[ \begin{array}{rrr} a & b & c \end{array} \right]^T ,\vec{v}=\left[ \begin{array}{rrr} d & e & f \end{array} \right]^T ,$ а$\vec{w}=\left[ \begin{array}{rrr} g & h & i \end{array} \right]^T .$ потім$\vec{u}\cdot \left(\vec{v}\times \vec{w}\right)$ коробковий добуток задається наступним. $$\begin{aligned} \vec{u}\cdot \left(\vec{v}\times \vec{w}\right) &= \left[ \begin{array}{r} a \\ b \\ c \end{array} \right] \cdot \left| \begin{array}{rrr} \vec{i} & \vec{j} & \vec{k} \\ d & e & f \\ g & h & i \end{array} \right| \\ &=a\left| \begin{array}{rr} e & f \\ h & i \end{array} \right| -b\left| \begin{array}{rr} d & f \\ g & i \end{array} \right| +c\left| \begin{array}{rr} d & e \\ g & h \end{array} \right| \\ &= \det \left[ \begin{array}{rrr} a & b & c \\ d & e & f \\ g & h & i \end{array} \right] \end{aligned}$$

Щоб взяти коробковий добуток, ви можете просто взяти детермінант матриці, яка призводить, дозволяючи рядкам бути складовими заданих векторів в тому порядку, в якому вони відбуваються в коробковому добутку.

Це випливає безпосередньо з визначення перехресного добутку, наведеного вище, і того, як ми розширюємо детермінанти. Таким чином, обсяг паралелепіпеда, що визначається векторами,$\vec{u},\vec{v},\vec{w}$ є всього лише абсолютним значенням вищевказаного детермінанта.