12.1: Вектори в площині

Last updated
Save as PDF

Page ID: 61592

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Цілі навчання

Опишіть плоский вектор, використовуючи правильні позначення.
Виконуйте основні векторні операції (скалярне множення, додавання, віднімання).
Висловіть вектор у вигляді компонента.
Поясніть формулу величини вектора.
Висловіть вектор через одиничні вектори.
Наведіть два приклади векторних величин.

При описі руху літака в польоті важливо повідомити дві частини інформації: напрямок, в якому рухається літак і швидкість літака. При вимірюванні такої сили, як тяга двигунів літака, важливо описати не тільки силу цієї сили, але і напрямок, в якому вона застосовується. Деякі величини, такі як або сила, визначаються як розміром (також називається величиною), так і напрямком. Величина, яка має величину і напрямок, називається вектором. У підручниках вектори часто позначаються жирними літерами, такими як$\mathbf{v}$. Оскільки важко писати чітким жирним шрифтом, коли ми пишемо вектори від руки, ми також включимо стрілку або гарпун над літерою, що представляє вектор. Щоб зробити вектори зрозумілішими в цьому підручнику (і посилити спосіб їх написання вручну), ми, як правило, будемо використовувати стрілки або гарпуни над жирними (або курсивними) літерами для представлення векторів, даючи нам$\vec v$ або$\vecs{v}$. Зауважте, що деякі цифри все одно використовуватимуть лише напівжирні літери для позначення векторів.

Визначення: Вектор

Вектор - це величина, яка має як величину, так і напрямок.

Векторне представлення

Вектор в площині представлений спрямованим відрізком лінії (стрілкою). Кінцеві точки відрізка називаються початковою точкою і кінцевою точкою вектора. Стрілка від початкової точки до кінцевої точки вказує напрямок вектора. Довжина відрізка лінії представляє його величину. Використовуємо позначення$\|\vecs{v}\|$ для позначення величини вектора$\vecs{v}$. Вектор з однаковою початковою і кінцевою точкою називається нульовим вектором, позначається$\vecs{0}$. Нульовий вектор є єдиним вектором без напрямку, і за умовністю можна вважати, що має будь-який напрямок, зручний для задачі під рукою.

Вектори з однаковою величиною і напрямком називаються еквівалентними векторами. Ми розглядаємо еквівалентні вектори як рівні, навіть якщо вони мають різні початкові точки. Таким чином, якщо$\vecs{v}$ і$\vecs{w}$ еквівалентні, пишемо

\[\vecs{v}=\vecs{w}. \nonumber \]

Визначення: Еквівалентні вектори

Вектори, як кажуть, є еквівалентними векторами, якщо вони мають однакову величину і напрямок.

Стрілки на малюнку$\PageIndex{1 (b)}$ рівнозначні. Кожна стрілка має однакову довжину і напрямок. Тісно пов'язаним поняттям є ідея паралельних векторів. Кажуть, що два вектори паралельні, якщо вони мають однакові або протилежні напрямки. Розглянемо цю ідею більш детально далі в розділі. Вектор визначається його величиною і напрямком, незалежно від того, де знаходиться його початкова точка.

Ця цифра має два зображення. Перший позначається як «a» і має відрізок лінії, що представляє вектор v. Відрізок лінії починається в початковій точці і йде до кінцевої точки. У кінцевій точці є наконечник стрілки. Друге зображення позначено «b» і являє собою п'ять векторів, кожен з яких позначений v sub 1, v sub 2, v sub 3, v sub 4, v sub 5. Всі вони спрямовані в одному напрямку і мають однакову довжину. — Рисунок$\PageIndex{1}$: (а) Вектор представлений спрямованим відрізком лінії від початкової точки до кінцевої точки. (b) Вектори$\vecs{v}_1$ через$\vecs{v}_5$ еквівалентні.

Використання жирних, малих літер для іменування векторів є загальним поданням у друку, але є альтернативні позначення. При написанні імені вектора від руки, наприклад, простіше накидати стрілку над змінною, ніж показати це вектор:$\vec{v}$. Коли вектор має початкову точку$P$ та кінцеву точку$Q$, позначення$\vecd{PQ}$ корисне, оскільки воно вказує напрямок та розташування вектора.

Приклад$\PageIndex{1}$: Sketching Vectors

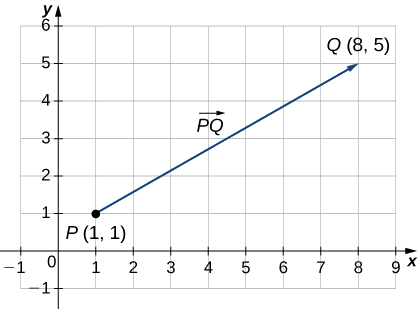
Намалюйте вектор на площині від початкової точки$P(1,1)$ до кінцевої точки$Q(8,5)$.

Рішення

Див$\PageIndex{2}$. Малюнок. Тому що вектор йде від точки$P$ до точки$Q$, ми називаємо його$\vecd{PQ}$.

Ця цифра є графіком першого квадранта. Існує відрізок лінії, що починається у впорядкованої пари (1, 1). Також цей пункт має маркування «П.» Відрізок лінії закінчується на впорядкованій парі (8, 5) і маркується «Q.» Відрізок лінії має маркування «PQ». — Малюнок$\PageIndex{2}$: Вектор з початковою точкою$(1,1)$ та кінцевою точкою$(8,5)$ називається$\vecd{PQ}$.

Вправа$\PageIndex{1}$

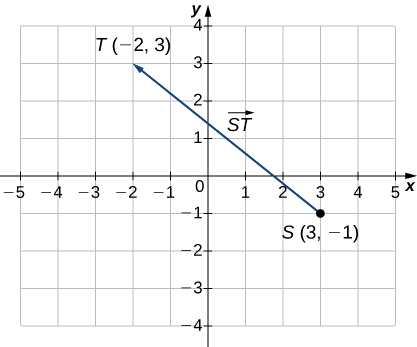
Намалюйте вектор$S$,$\vecd{ST}$ де точка$(3,−1)$ і$T$ точка$(−2,3).$

Підказка: Перша точка, вказана в назві вектора, є початковою точкою вектора.

Відповідь: $Ця цифра являє собою графік системи координат. Існує відрізок лінії, що починається у впорядкованої пари (3, -1). Також цей пункт має маркування «S.» Відрізок лінії закінчується на впорядкованій парі (-2, 3) і маркується «Т». У точці «T» є стрілка, що представляє вектор. Відрізок лінії маркується «ST.»$

Поєднання векторів

Вектори мають багато реальних застосувань, включаючи ситуації, пов'язані з силою або швидкістю. Наприклад, розглянемо сили, що діють на човні, що перетинає річку. Мотор човна генерує силу в одному напрямку, а протягом річки генерує силу в іншому напрямку. Обидві сили є векторами. Ми повинні враховувати як величину, так і напрямок кожної сили, якщо хочемо знати, куди піде човен.

Другий приклад, який включає вектори є захисник кидає футбол. Квотербек не кидати м'яч паралельно землі; замість цього, він спрямований вгору в повітря. Швидкість його кидка може бути представлена вектором. Якщо ми знаємо, наскільки сильно він кидає м'яч (величина - в даному випадку швидкість) і кут (напрямок), ми можемо сказати, як далеко м'яч пройде вниз по полю.

Справжнє число часто називають скалярним в математиці і фізиці. На відміну від векторів, скаляри, як правило, вважають, що мають лише величину, але не напрямок. Множення вектора на скаляр змінює величину вектора. Це називається скалярним множенням. Зверніть увагу, що зміна величини вектора не вказує на зміну його напрямку. Наприклад, вітер, що дме з півночі на південь, може збільшуватися або зменшуватися, зберігаючи свій напрямок з півночі на південь.

Визначення: Скалярне множення

$k\vecs{v}$Добуток вектора$\vecs{v}$ і скаляра$k$ - це вектор з величиною, яка в$|k|$ рази перевищує величину$\vecs{v}$, і з напрямком, який збігається з напрямком$\vecs{v}$ if$k>0$, і протилежним напрямку$\vecs{v}$ if$k<0$. Це називається скалярним множенням. Якщо$k=0$ або$\vecs{v}=\vecs{0}$, то$k\vecs{v}=\vecs{0}.$

Як і слід було очікувати, якщо$k=−1$, ми позначимо продукт$k\vecs{v}$ як

\[k\vecs{v}=(−1)\vecs{v}=−\vecs{v}. \nonumber \]

Зверніть увагу, що$−\vecs{v}$ має таку ж величину$\vecs{v}$, що і, але має зворотний напрямок (рис.$\PageIndex{3}$).

Ця графіка має 4 цифри. Перший малюнок являє собою вектор з написом «v.» Друга цифра є вектором в два рази довшою за перший вектор і має позначку «2 v.» Третя цифра вдвічі менше першої і має маркування «1/2 v.» Четверта фігура є вектором у зворотному напрямку, як і перша. Він позначений як «-v.» — Рисунок$\PageIndex{3}$: (a) Вихідний вектор$ \vecs{v}$ має$n$ одиниці довжини. (b) Довжина$2 \vecs{v}$ дорівнює$2n$ одиницям. (c) Довжина$n/2$ одиниць.$ \vecs{v}/2$ (d) вектори$\vecs{v}$$−\vecs{v}$ мають однакову довжину, але протилежні напрямки.

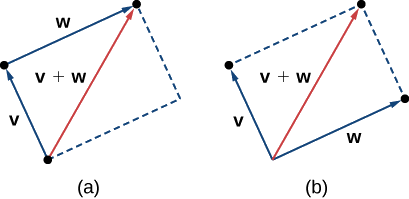
Ще одна операція, яку ми можемо виконати над векторами, полягає в тому, щоб скласти їх разом у векторному додаванні, але оскільки кожен вектор може мати свій напрямок, процес відрізняється від додавання двох чисел. Найпоширенішим графічним методом додавання двох векторів є розміщення початкової точки другого вектора в кінцевій точці першого, як на малюнку$\PageIndex{4 (a)}$. Щоб зрозуміти, чому це має сенс, припустимо, наприклад, що обидва вектори представляють зміщення. Якщо об'єкт рухається спочатку від початкової точки до кінцевої точки вектора$\vecs{v}$, потім від початкової точки до кінцевої точки вектора$\vecs{w}$, загальне зміщення таке ж, як якби об'єкт здійснив лише один рух від початкової точки до кінцевої точки вектора $\vecs{v}+\vecs{w}$. Зі зрозумілих причин такий підхід називається методом трикутника. Зверніть увагу, що якби ми переключили порядок, так що це$\vecs{w}$ був наш перший вектор і$\vecs{v}$ був наш другий вектор, ми б опинилися в тому ж місці. (Знову див$\PageIndex{4 (a)}$. Рис.) Таким чином,

\[ \vecs{v}+ \vecs{w}= \vecs{w}+ \vecs{v}. \nonumber \]

Другий метод додавання векторів називається методом паралелограма. За допомогою цього методу ми розміщуємо два вектори так, щоб вони мали однакову початкову точку, а потім малюємо паралелограм з векторами як дві сусідні сторони, як на малюнку$\PageIndex{4 (b)}$. Довжина діагоналі паралелограма - це сума. Порівнюючи$\PageIndex{4 (b)}$ Figure і Figure$\PageIndex{4 (a)}$, ми бачимо, що отримуємо однакову відповідь, використовуючи будь-який метод. Вектор$ \vecs{v}+ \vecs{w}$ називається векторною сумою.

Визначення: Векторне додавання

Сума двох векторів$\vecs{v}$ і$\vecs{w}$ може бути побудована графічно, розмістивши початкову точку$\vecs{w}$ в кінцевій точці$\vecs{v}$. Потім, векторна сума$\vecs{v}+\vecs{w}$, - це вектор з початковою точкою, яка збігається з початковою точкою$\vecs{v}$ і має кінцеву точку, яка збігається з кінцевою точкою$\vecs{w}$. Ця операція відома як векторне додавання.

Це зображення має дві фігури. Перший має два вектори, v і w з однаковою початковою точкою. Паралелограм утворюється шляхом накреслення ламаних ліній, паралельних двом векторам. Від тієї ж початкової точки до протилежного кута проводиться діагональна лінія. Він має маркування «v + w». Другий має два вектори, v і w. Вектор v починається в кінцевій точці вектора w. Паралелограм утворюється шляхом замальовування ламаних ліній, паралельних двом векторам. Діагональна лінія проводиться від тієї ж початкової точки, що і вектор w, до протилежного кута. Він має маркування «v + w». — Рисунок$\PageIndex{4}$: (а) При додаванні векторів методом трикутника початковою точкою$\vecs{w}$ є кінцева точка$\vecs{v}$. (б) При додаванні векторів методом паралелограма вектори$\vecs{v}$ і$\vecs{w}$ мають однакову початкову точку.

Тут також доречно обговорити векторне віднімання. Визначаємо$\vecs{v}−\vecs{w}$ як$\vecs{v}+(−\vecs{w})=\vecs{v}+(−1)\vecs{w}$. Вектор$\vecs{v}−\vecs{w}$ називається різницею векторів. Графічно вектор$\vecs{v}−\vecs{w}$ зображується шляхом малювання вектора від кінцевої точки$\vecs{w}$ до кінцевої точки$\vecs{v}$ (рис.$\PageIndex{5}$).

Це зображення має дві фігури. Перша цифра має два вектори, один з яких позначений «v», а інший з позначкою «w». Обидва вектори мають однакову початкову точку. Третій вектор малюється між кінцевими точками v і w і позначається як «v — w». Друга цифра має два вектори, один з яких позначений «v», а інший з позначкою «-w». Вектор «-w» має свою початкову точку в кінцевій точці «v.» Паралелограм створюється з ламаними лініями, де «v» - діагональ, а «w» - верхня сторона. — Малюнок$\PageIndex{5}$: (а) Різниця векторів$\vecs{v}−\vecs{w}$ зображується шляхом малювання вектора від кінцевої точки$\vecs{w}$ до кінцевої точки$\vecs{v}$. (b) Вектор$\vecs{v}−\vecs{w}$ еквівалентний вектору$\vecs{v}+(−\vecs{w})$.

На$\PageIndex{4 (a)}$ малюнку початковою точкою$\vecs{v}+\vecs{w}$ є початкова точка$\vecs{v}$. Кінцева точка$\vecs{v}+\vecs{w}$ є кінцевою точкою$\vecs{w}$. Ці три вектори утворюють сторони трикутника. Звідси випливає, що довжина будь-якої однієї сторони менше суми довжин інших сторін. Отже, у нас є

\[\|\vecs{v}+\vecs{w}\|≤\|\vecs{v}\|+\|\vecs{w}\|. \nonumber \]

Це більш широко відомо як нерівність трикутника. Однак є один випадок, коли результуючий вектор$\vecs{u}+\vecs{v}$ має таку ж величину, як і сума величин$\vecs{u}$ і$\vecs{v}$. Це відбувається тільки тоді, коли$\vecs{u}$ і$\vecs{v}$ мають однаковий напрямок.

Приклад$\PageIndex{2}$: Combining Vectors

Враховуючи вектори$\vecs{v}$ і$\vecs{w}$ показані на малюнку$\PageIndex{6}$, намалюйте вектори

$3\vecs{w}$
$\vecs{v}+\vecs{w}$
$2\vecs{v}−\vecs{w}$

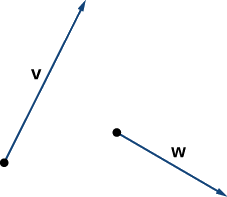
Ця цифра має два вектори. Це вектор v і вектор w, вони не пов'язані між собою. — Малюнок$\PageIndex{6}$: Вектори$\vecs{v}$ і$\vecs{w}$ лежать в одній площині.

Рішення

a Вектор$3\vecs{w}$ має той самий напрямок, що і$\vecs{w}$; він втричі довший, ніж$\vecs{w}$.

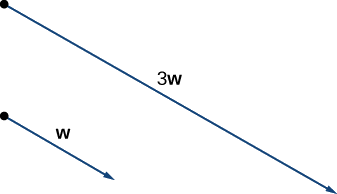
$Ця цифра має два вектори. Перший має маркування «w». Другий паралельний «w» і має маркування «3w». Це в три рази довше, ніж w в одному напрямку.$

Вектор$3\vecs{w}$ має такий же напрямок, як$\vecs{w}$ і в три рази довше.

б Використовуйте будь-який метод додавання, щоб знайти$\vecs{v}+\vecs{w}$.

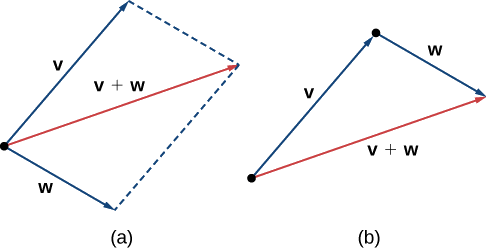
Це зображення має дві фігури. Перший має два вектори, позначені «v» і «w». Вони обидва мають однакову початкову точку. Намальовано третій вектор з написом «v + w». Це діагональ паралелограма, утворена наявністю сторін, паралельних векторам v і w. Друга фігура являє собою трикутник, утворений наявністю вектора v з одного боку і вектора w, прилеглого до v. Кінцева точка v є початковою точкою w. Третя сторона позначена як «v + w». — Малюнок$\PageIndex{7}$: Щоб знайти$\vecs{v}+\vecs{w}$, вирівняйте вектори в їх початкових точках або помістіть початкову точку одного вектора в кінцевій точці іншого. (а) Вектор$\vecs{v}+\vecs{w}$ - діагональ паралелограма зі сторонами$\vecs{v}$ і$\vecs{w}$. (b) Вектор$\vecs{v}+\vecs{w}$ - це третя сторона трикутника, утвореного з$\vecs{w}$ розміщеними в кінцевій точці$\vecs{v}$.

c Щоб знайти$2\vecs{v}−\vecs{w}$, ми можемо спочатку переписати вираз як$2\vecs{v}+(−\vecs{w})$. Потім ми можемо намалювати вектор$−\vecs{w}$, а потім додати його до вектора$2\vecs{v}$.

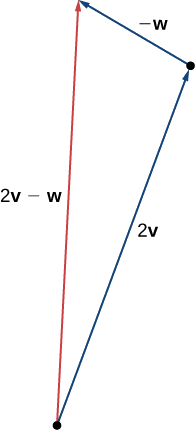
Ця фігура являє собою трикутник, утворений наявністю вектора 2v з одного боку і вектора -w, прилеглого до 2v. Кінцева точка 2v - початкова точка -w. Третя сторона має маркування «2v - w». — Малюнок$\PageIndex{8}$: Щоб знайти$2\vecs{v}−\vecs{w}$, просто додайте$2\vecs{v}+(−\vecs{w})$.

Вправа$\PageIndex{2}$

Використовуючи вектори$\vecs{v}$ та$\vecs{w}$ з$\PageIndex{2}$ Example, намалюйте вектор$2\vecs{w}−\vecs{v}$.

Підказка: Перший ескіз векторів$2\vecs{w}$ і$−\vecs{v}$.

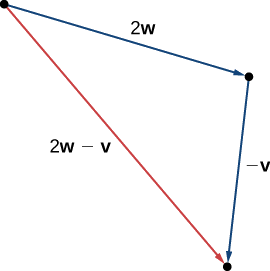
Відповідь: $Ця фігура являє собою трикутник, утворений наявністю вектора 2w з одного боку і вектора -v, прилеглого до 2w. Кінцева точка 2w є початковою точкою -v. Третя сторона має маркування «2w — v.»$

Векторні компоненти

Працювати з векторами в площині простіше, коли ми працюємо в системі координат. Коли початкові точки та кінцеві точки векторів задані в декартових координатах, обчислення стають прямими.

Приклад$\PageIndex{3}$: Comparing Vectors

Є$\vecs{v}$ і$\vecs{w}$ еквівалентні вектори?

а.

$\vecs{v}$має початкову точку$(3,2)$ та кінцеву точку$(7,2)$
$\vecs{w}$має початкову точку$(1,−4)$ та кінцеву точку$(1,0)$

б.

$\vecs{v}$має початкову точку$(0,0)$ та кінцеву точку$(1,1)$
$\vecs{w}$має початкову точку$(−2,2)$ та кінцеву точку$(−1,3)$

Рішення

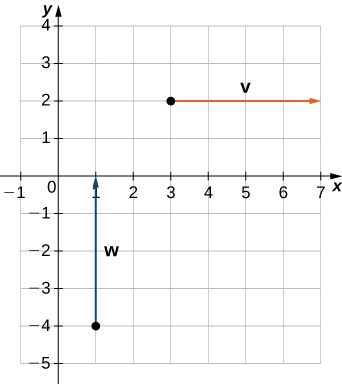
а Вектори - це кожна$4$ одиниця довжини, але вони орієнтовані в різні боки. Так$\vecs{v}$ і не$\vecs{w}$ рівнозначні (рис.$\PageIndex{9}$).

Ця фігура являє собою декартову систему координат з двома векторами. Перший вектор з позначкою «v» має початкову точку в (3, 2) і кінцеву точку (7, 2). Вона паралельна осі х. Другий вектор позначений «w» і має початкову точку (1, -4) і кінцеву точку (1, 0). Він паралельний осі y. — Малюнок$\PageIndex{9}$: Ці вектори не є еквівалентними.

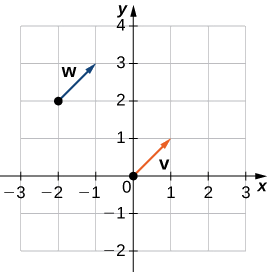
б Виходячи з малюнка$\PageIndex{10}$, і використовуючи трохи геометрії, зрозуміло, що ці вектори мають однакову довжину і однаковий напрямок, тому$\vecs{v}$ і$\vecs{w}$ еквівалентні.

Ця фігура являє собою декартову систему координат з двома векторами. Перший вектор з міткою «v» має початкову точку (0, 0) та кінцеву точку (1, 1). Другий вектор позначений «w» і має початкову точку (-2, 2) і кінцеву точку (-1, 3). — Малюнок$\PageIndex{10}$: Ці вектори еквівалентні.

Вправа$\PageIndex{3}$

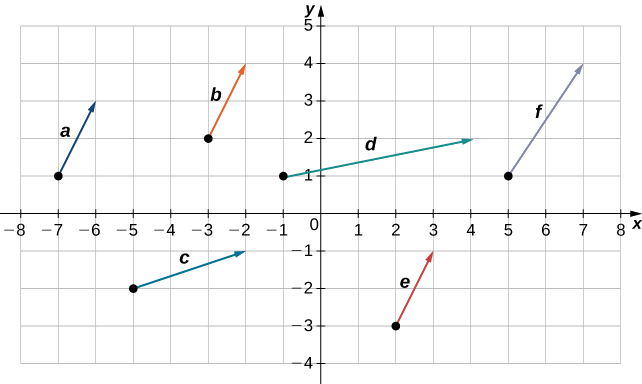
Які з наступних векторів еквівалентні?

$Ця фігура являє собою систему координат з 6 векторами, кожен з яких позначений від a до f. Три вектори «a», «b» і «e» мають однакову довжину і спрямовані в одному напрямку.$

Підказка: Еквівалентні вектори мають однакову величину і однаковий напрямок.

Відповідь: Вектори$\vecs{a}, \vecs{b}$, і$\vecs{e}$ еквівалентні.

Ми бачили, як побудувати вектор, коли нам дають початкову точку та кінцеву точку. Однак, оскільки вектор може бути розміщений в будь-якому місці площини, може бути простіше виконати обчислення з вектором, коли його початкова точка збігається з початковою точкою. Вектор з початковою точкою в початковій точці ми називаємо вектором стандартної позиції. Оскільки початкова точка будь-якого вектора в стандартному положенні, як відомо$(0,0)$, ми можемо описати вектор, дивлячись на координати його кінцевої точки. Таким чином, якщо вектор$\vecs{v}$ має свою початкову точку на початку та кінцеву точку,$(x,y),$ ми запишемо вектор у вигляді компонента як

\[\vecs{v}=⟨x,y⟩. \nonumber \]

Коли вектор записується у вигляді компонента, подібного до цього, скаляри x і y називаються складовими$\vecs{v}$.

Визначення: Векторні компоненти

Вектор з початковою точкою$(0,0)$ та кінцевою точкою$(x,y)$ можна записати у вигляді компонента як

\[\vecs{v}=⟨x,y⟩. \nonumber \]

Скаляри$x$ і$y$ називаються складовими$\vecs{v}$.

Нагадаємо, що вектори називаються малими літерами жирним шрифтом або шляхом малювання стрілки над їх назвою. Ми також дізналися, що ми можемо назвати вектор за його складовою формою, з координатами його кінцевої точки в кутових дужках. Однак при написанні складової форми вектора важливо розрізняти$⟨x,y⟩$ і$(x,y)$. Перша впорядкована пара використовує кутові дужки для опису вектора, тоді як друга використовує дужки для опису точки в площині. Початкова точка$⟨x,y⟩$ є$(0,0)$; кінцева точка$⟨x,y⟩$ є$(x,y)$.

Коли у нас вектор ще не знаходиться в стандартному положенні, ми можемо визначити його складову форму одним з двох способів. Ми можемо використовувати геометричний підхід, при якому ми накидаємо вектор в координатній площині, а потім ескізуємо еквівалентний вектор стандартного положення. Крім того, ми можемо знайти його алгебраїчно, використовуючи координати початкової точки та кінцевої точки. Щоб знайти його алгебраїчно, ми віднімаємо$x$ -координату початкової точки з$x$ -координати кінцевої точки, щоб отримати$x$ -компонент, і віднімаємо$y$ -координату початкової точки з$y$ -координати кінцевої точки, щоб отримати$y$ -компонентний.

Правило: Компонентна форма вектора

$\vecs{v}$Дозволяти вектор з початковою точкою$(x_i,y_i)$ та кінцевою точкою$(x_t,y_t)$. Тоді ми можемо висловити$\vecs{v}$ в складовій формі як$\vecs{v}=⟨x_t−x_i,y_t−y_i⟩$.

Приклад$\PageIndex{4}$: Expressing Vectors in Component Form

Експрес-вектор$\vecs{v}$ з початковою точкою$(−3,4)$ та кінцевою точкою$(1,2)$ у вигляді компонента.

Рішення:

a. геометричні

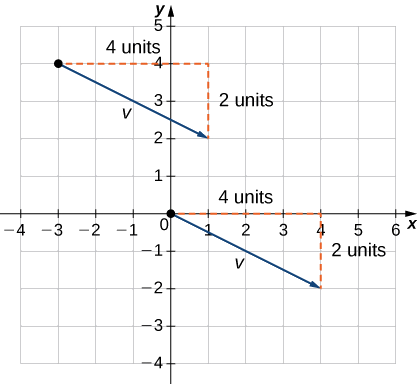
1. Намалюйте вектор в координатній площині (рис.$\PageIndex{11}$).

2. Кінцева точка - 4 одиниці вправо і 2 одиниці вниз від початкової точки.

3. Знайдіть точку, яка становить 4 одиниці праворуч і 2 одиниці вниз від початку.

4. У стандартному положенні цей вектор має початкову точку$(0,0)$ та кінцеву точку$(4,−2)$:

$\vecs{v}=⟨4,−2⟩.$

Ця цифра є системою координат. На графіку є два вектори. Перший вектор має початкову точку на початку та кінцеву точку на (4, -2). Горизонтальна відстань від початкової до кінцевої точки для вектора позначається як «4 одиниці». Відстань по вертикалі від початкової до кінцевої точки маркується як «2 одиниці». Другий вектор має початкову точку в (-3, 4) і кінцеву точку в (1, 2). Горизонтальна відстань від початкової до кінцевої точки для вектора позначається як «4 одиниці». Відстань по вертикалі від початкової до кінцевої точки маркується як «2 одиниці». — Малюнок$\PageIndex{11}$: Ці вектори еквівалентні.

б. алгебраїчна

У першому рішенні ми використовували ескіз вектора, щоб побачити, що кінцева точка лежить на 4 одиницях праворуч. Ми можемо досягти цього алгебраїчно, знайшовши різницю в$x$ -координатах:

$x_t−x_i=1−(−3)=4.$

Аналогічно різниця$y$ -координат показує вертикальну довжину вектора.

$y_t−y_i=2−4=−2.$

Отже, в складовій формі,

$\vecs{v}=⟨x_t−x_i,y_t−y_i⟩=⟨1−(−3),2−4⟩=⟨4,−2⟩.$

Вправа$\PageIndex{4}$

Вектор$\vecs{w}$ має початкову точку$(−4,−5)$ та кінцеву точку$(−1,2)$. Експрес$\vecs{w}$ в складовій формі.

Підказка: Ви можете використовувати геометричний або алгебраїчний метод.

Відповідь: $⟨3,7⟩$

Щоб знайти величину вектора, обчислюємо відстань між його початковою точкою та кінцевою точкою. Величина вектора$\vecs{v}=⟨x,y⟩$ позначається$\|\vecs{v}\|,$ або$|\vecs{v}|$, і може бути обчислена за формулою

\[\|\vecs{v}\|=\sqrt{x^2+y^2}. \nonumber \]

Зауважте, що оскільки цей вектор записаний у вигляді компонента, він еквівалентний вектору в стандартному положенні, з початковою точкою в початковій та кінцевій точці$(x,y)$. Таким чином, досить обчислити величину вектора в стандартному положенні. Використовуючи формулу відстані для обчислення відстані між початковою точкою$(0,0)$ та кінцевою точкою$(x,y)$, ми маємо

\[\|\vecs{v}\|=\sqrt{(x−0)^2+(y−0)^2}=\sqrt{x^2+y^2}. \nonumber \]

Виходячи з цієї формули, зрозуміло, що для будь-якого вектора$\vecs{v}, \|\vecs{v}\|≥0,$ і$\|\vecs{v}\|=0$ якщо і тільки якщо$\vecs{v}=\vecs{0}$.

Величина вектора також може бути виведена за допомогою теореми Піфагора, як на наступному малюнку.

Ця фігура являє собою прямокутний трикутник. Обидві сторони позначені як «x» та «y». Гіпотенуза представлена у вигляді вектора і позначена «квадратний корінь (x^2 + y^2)». — Малюнок$\PageIndex{12}$: Якщо ви використовуєте компоненти вектора для визначення прямокутного трикутника, величина вектора дорівнює довжині гіпотенузи трикутника.

Визначено скалярне множення та векторне додавання геометрично. Експресія векторів у компонентній формі дозволяє нам виконувати ці самі операції алгебраїчно.

Визначення: Скалярне множення та додавання векторів

$\vecs{v}=⟨x_1,y_1⟩$$\vecs{w}=⟨x_2,y_2⟩$Дозволяти і бути вектори, і нехай$k$ бути скалярним.

Скалярне множення:\[k\vecs{v}=⟨kx_1,ky_1⟩ \nonumber \]
Векторне додавання:\[\vecs{v}+\vecs{w}=⟨x_1,y_1⟩+⟨x_2,y_2⟩=⟨x_1+x_2,y_1+y_2⟩ \nonumber \]

Приклад$\PageIndex{5}$: Performing Operations in Component Form

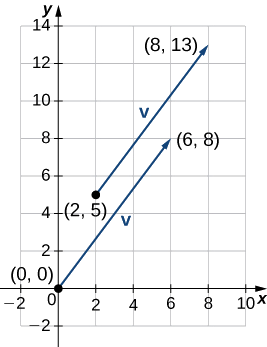
$\vecs{v}$Дозволяти вектор з початкової точки$(2,5)$ і кінцевої точки$(8,13)$, і нехай$\vecs{w}=⟨−2,4⟩$.

$\vecs{v}$Висловіть у складовій формі і знайдіть$\|\vecs{v}\|$. Потім, використовуючи алгебру, знайдіть
$\vecs{v}+\vecs{w}$,
$3\vecs{v}$, і
$\vecs{v}−2\vecs{w}$.

Рішення

а. щоб помістити початкову точку$\vecs{v}$ на початку, ми повинні перевести вектор на 2 одиниці вліво і 5 одиниць вниз (рис.$\PageIndex{13}$). Використовуючи алгебраїчний метод, ми можемо висловити$\vecs{v}$ як$\vecs{v}=⟨8−2,13−5⟩=⟨6,8⟩$:

$\|\vecs{v}\|=\sqrt{6^2+8^2}=\sqrt{36+64}=\sqrt{100}=10$.

Ця цифра є першим квадрантом системи координат. Він має два вектори. Перший вектор має початкову точку в (2, 5) і кінцеву точку (8, 13). Другий вектор має початкову точку на початку та кінцеву точку в (6, 8). — Малюнок$\PageIndex{13}$: У складовій формі,$\vecs{v}=⟨6,8⟩$.

b. щоб знайти$\vecs{v}+\vecs{w}$, додайте$x$ -компоненти та$y$ -компоненти окремо:

$\vecs{v}+\vecs{w}=⟨6,8⟩+⟨−2,4⟩=⟨4,12⟩.$

с. щоб знайти$3\vecs{v}$,$\vecs{v}$ помножте на скаляр$k=3$:

$3\vecs{v}=3⋅⟨6,8⟩=⟨3⋅6,3⋅8⟩=⟨18,24⟩.$

d. знайти$\vecs{v}−2\vecs{w}$, знайти$−2\vecs{w}$ і додати його в$\vecs{v}:$

$\vecs{v}−2\vecs{w}=⟨6,8⟩−2⋅⟨−2,4⟩=⟨6,8⟩+⟨4,−8⟩=⟨10,0⟩.$

Вправа$\PageIndex{5A}$

Дозволяти$\vecs{a}=⟨7,1⟩$ і$\vecs{b}$ нехай вектор з початковою точкою$(3,2)$ і кінцевою точкою$(−1,−1).$

Знайти$\|\vecs{a}\|$.
Експрес$\vecs{b}$ в складовій формі.
Знайти$3\vecs{a}−4\vecs{b}.$

Підказка: Використовуйте теорему Піфагора, щоб знайти$\|\vecs{a}\|$. Щоб знайти$3\vecs{a}−4\vecs{b}$, почніть з знаходження скалярних кратних$3\vecs{a}$ і$−4\vecs{b}$.

Відповідь: $\|\vecs{a}\|=5\sqrt{2},$
Відповідь б: $\vecs{b}=⟨−4,−3⟩,$
Відповідь c: $3\vecs{a}−4\vecs{b}=⟨37,15⟩$

Тепер, коли ми встановили основні правила векторної арифметики, ми можемо констатувати властивості векторних операцій. Ми доведемо два цих властивості. Інші можуть бути доведені подібним чином.

Властивості векторних операцій

Дозволяти$\vecs{u}, \, \vecs{v}$, і$\vecs{w}$ бути вектори в площині. $s$Дозволяти$r$ і бути скалярами.

Комутативне майно\[\vecs{u}+\vecs{v}=\vecs{v}+\vecs{u} \label{commutative} \]
Асоціативна властивість\[(\vecs{u}+\vecs{v})+\vecs{w}=\vecs{u}+(\vecs{v}+\vecs{w}) \nonumber \]
Властивість адитивної ідентичності\[\vecs{u}+\vecs{0}=\vecs{u} \nonumber \]
Адитивна зворотна властивість\[\vecs{u}+(−\vecs{u})=\vecs{0} \nonumber \]
Асоціативність скалярного множення\[r(s\vecs{u})=(rs)\vecs{u} \nonumber \]
Розподільна власність\[(r+s)\vecs{u}=r\vecs{u}+s\vecs{u} \label{Distributive} \]
Розподільна власність\[r(\vecs{u}+\vecs{v})=r\vecs{u}+r\vecs{v} \nonumber \]
Ідентичність і нульові властивості\[1\vecs{u}=\vecs{u}, \, 0\vecs{u}=\vecs{0} \nonumber \]

Доказ Комутативного майна

Дозвольте$\vecs{u}=⟨x_1,y_1⟩$ і$\vecs{v}=⟨x_2,y_2⟩.$ застосовуйте комутативне властивість для дійсних чисел:

\[ \begin{align*} \vecs{u}+\vecs{v} =⟨x_1+x_2,y_1+y_2⟩ \\[4pt] = ⟨x_2+x_1,y_2+y_1⟩ \\[4pt] = \vecs{v}+\vecs{u}. \end{align*}\]

□

Доказ розподільної власності

Застосовуємо розподільну властивість для дійсних чисел:

\[ \begin{align*} r(\vecs{u}+\vecs{v}) =r⋅⟨x_1+x_2,y_1+y_2⟩ \\[4pt] =⟨r(x_1+x_2),r(y_1+y_2)⟩ \\[4pt] = ⟨rx_1+rx_2,ry_1+ry_2⟩ \\[4pt] = ⟨rx_1,ry_1⟩+⟨rx_2,ry_2⟩ \\[4pt] = r\vecs{u}+r\vecs{v}. \end{align*}\]

□

Вправа$\PageIndex{5B}$

Доведіть адитивну обернену властивість.

Підказка: Використовуйте складову форму векторів.

Ми знайшли складові вектора за його початковою та кінцевою точками. У деяких випадках ми можемо мати лише величину та напрямок вектора, а не точки. Для цих векторів ми можемо визначити горизонтальну і вертикальну складові за допомогою тригонометрії (рис.$\PageIndex{14}$).

Ця фігура являє собою прямокутний трикутник. Є кут, позначений тета. Обидві сторони позначені «величиною v разів косинус тета» і «величина v разів синус тета». Гіпотенуза має маркування «величина v.» — Малюнок$\PageIndex{14}$: Компоненти вектора утворюють катети прямокутного трикутника, причому вектор - гіпотенуза.

Розглянемо кут,$θ$ утворений вектором$\vecs{v}$ і позитивною$x$ -віссю. З трикутника ми бачимо, що$\vecs{v}$ складові вектора$⟨\|\vecs{v}\| \cos{θ}, \, \|\vecs{v}\| \sin {θ}⟩$. Тому, враховуючи кут і величину вектора, ми можемо використовувати косинус і синус кута, щоб знайти складові вектора.

Приклад$\PageIndex{6}$: Finding the Component Form of a Vector Using Trigonometry

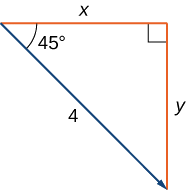
Знайти складову форму вектора з величиною 4, яка утворює кут$−45°$ з$x$ віссю -.

Рішення

$x$Дозволити і$y$ представляти складові вектора (рис.$\PageIndex{15}$). Потім$x=4 \cos(−45°)=2 \sqrt{2}$ і$y=4 \sin(−45°)=−2\sqrt{2}$. Компонентною формою вектора є$⟨2\sqrt{2},−2\sqrt{2}⟩$.

Ця фігура являє собою прямокутний трикутник. Обидві сторони позначені як «x» та «y». Гіпотенуза має маркування «4». Є також кут з написом «45 градусів». Гіпотенуза представлена у вигляді вектора. — Малюнок$\PageIndex{15}$: Використовуйте тригонометричні коефіцієнти,$x=\|\vecs{v}\| \cos θ$ а *$y=\|\vecs{v}\| \sin θ,$*для ідентифікації складових вектора.

Вправа$\PageIndex{6}$

Знайти складову форму вектора$\vecs{v}$ з величиною 10, яка утворює кут з$120°$ додатною$x$ - віссю.

Підказка: $x=\|\vecs{v}\| \cos θ$і$y=\|\vecs{v}\| \sin θ$
Відповідь: $\vecs v=⟨−5,5\sqrt{3}⟩$

Одиниця Вектори

Одиничний вектор - це вектор з величиною$1$. Для будь-якого ненульового вектора ми можемо використовувати скалярне множення$\vecs{v}$, щоб знайти одиничний вектор$\vecs{u}$, який має той самий напрямок, що і$\vecs{v}$. Для цього множимо вектор на зворотну його величині:

\[\vecs{u}=\dfrac{1}{\|\vecs{v}\|} \vecs{v}. \nonumber \]

Нагадаємо, що коли ми визначили скалярне множення, ми зазначили, що$\|k\vecs{v}\| =|k|⋅\|\vecs{v}\| $. Бо$\vecs{u}=\dfrac{1}{\|\vecs{v}\| }\vecs{v}$, з цього випливає$\|\vecs{u}\| =\dfrac{1}{\|\vecs{v}\| }(\|\vecs{v}\| )=1$. Ми говоримо, що$\vecs{u}$ це одиничний вектор в напрямку$\vecs{v}$ (рис.$\PageIndex{16}$). Процес використання скалярного множення для знаходження одиничного вектора із заданим напрямком називається нормалізацією.

Це зображення має дві фігури. Перший - вектор з написом «v.» Друга фігура являє собою вектор в тому ж напрямку з написом «u». Цей вектор має довжину 1 одиницю. — Малюнок$\PageIndex{16}$: Вектор$\vecs{v}$ і пов'язаний з ним одиничний вектор$\vecs{u}=\dfrac{1}{\|\vecs{v}\|}\vecs{v}$. У цьому випадку$\|\vecs{v}\|>1.$

Приклад$\PageIndex{7}$: Finding a Unit Vector

Нехай$\vecs{v}=⟨1,2⟩$.

Знайдіть одиничний вектор з тим же напрямком, що і$\vecs{v}$.
Знайдіть вектор$\vecs{w}$ з таким же напрямком, як$\vecs{v}$ такий, що$\|\vecs{w}\|=7$.

Рішення:

а. спочатку знайдіть величину$\vecs{v}$, потім розділіть складові$\vecs{v}$ на величину:

\[\|\vecs{v}\|=\sqrt{1^2+2^2}=\sqrt{1+4}=\sqrt{5} \nonumber \]

\[\vecs{u}=\dfrac{1}{\|\vecs{v}\|}\vecs{v}=\dfrac{1}{\sqrt{5}}⟨1,2⟩=⟨\dfrac{1}{\sqrt{5}},\dfrac{2}{\sqrt{5}}⟩ \nonumber. \nonumber \]

б. вектор$\vecs{u}$ знаходиться в тому ж напрямку, що$\vecs{v}$ і$\|\vecs{u}\|=1$. Використовуйте скалярне множення, щоб збільшити довжину$\vecs{u}$ без зміни напрямку:

\[\vecs{w}=7\vecs{u}=7⟨\dfrac{1}{\sqrt{5}},\dfrac{2}{\sqrt{5}}⟩=⟨\dfrac{7}{\sqrt{5}},\dfrac{14}{\sqrt{5}}⟩ \nonumber. \nonumber \]

Вправа$\PageIndex{7}$

Нехай$\vecs{v}=⟨9,2⟩$. Знайти вектор з величиною$5$ в протилежному напрямку як$\vecs{v}$.

Підказка: Спочатку знайдіть одиничний вектор в тому ж напрямку, що і$\vecs{v}$.
Відповідь: $⟨−\dfrac{45}{\sqrt{85}},−\dfrac{10}{\sqrt{85}}⟩$

Ми бачили, наскільки зручно може бути написання вектора в компонентному вигляді. Іноді, правда, зручніше писати вектор у вигляді суми горизонтального вектора і вертикального вектора. Щоб зробити це простіше, давайте розглянемо стандартні одиничні вектори. Стандартними одиничними векторами є вектори$\hat{\mathbf i}=⟨1,0⟩$ і$\hat{\mathbf j}=⟨0,1⟩$ (рис.$\PageIndex{17}$).

Ця цифра має осі x та y системи координат у першому квадранті. На осі x є вектор з міткою «i», який дорівнює <1,0 — Малюнок$\PageIndex{17}$: Стандартні одиничні вектори$\hat{\mathbf i}$ і$\hat{\mathbf j}$.

Застосовуючи властивості векторів, можна висловити будь-який вектор через$\hat{\mathbf i}$ і$\hat{\mathbf j}$ в тому, що ми називаємо лінійною комбінацією:

\[\vecs{v}=⟨x,y⟩=⟨x,0⟩+⟨0,y⟩=x⟨1,0⟩+y⟨0,1⟩=x\hat{\mathbf i}+y\hat{\mathbf j}. \nonumber \]

Таким чином,$\vecs{v}$ це сума горизонтального вектора з величиною$x$, і вертикального вектора з величиною$y$, як на малюнку$\PageIndex{18}$.

Ця фігура являє собою прямокутний трикутник. Горизонтальна сторона має маркування «xi». Вертикальна сторона має маркування «yj». Гіпотенуза являє собою вектор з міткою «v.» — Малюнок$\PageIndex{18}$: Вектор$\vecs{v}$ є сумою$x\hat{\mathbf i}$ і$y\hat{\mathbf j}$.

Приклад$\PageIndex{8}$: Using Standard Unit Vectors

Висловіть вектор$\vecs{w}=⟨3,−4⟩$ через стандартні одиничні вектори.
Вектор$\vecs{u}$ - це одиничний вектор, який утворює кут$60°$ з додатною$x$ -віссю. Використовуйте стандартні одиничні вектори для опису$\vecs{u}$.

Рішення:

a. розв'язати вектор$\vecs{w}$ у вектор з нульовим$y$ -компонентом і вектор з нульовим$x$ -компонентом:

\[\vecs{w}=⟨3,−4⟩=3 \hat{\mathbf i}−4 \hat{\mathbf j}. \nonumber \]

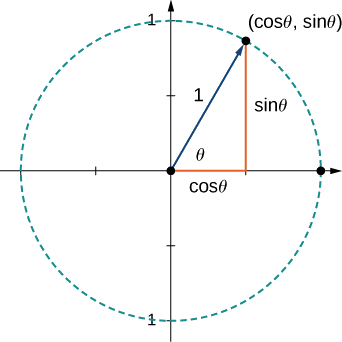
б. оскільки$\vecs{u}$ є одиничним вектором, кінцева точка лежить на одиничному колі, коли вектор розміщений в стандартному положенні (рис.$\PageIndex{19}$).

\[ \begin{align*} \vecs{u} =⟨\cos 60°,\sin 60°⟩ \\[4pt] =⟨\dfrac{1}{2},\dfrac{\sqrt{3}}{2}⟩ \\[4pt] = \dfrac{1}{2} \hat{\mathbf i}+\dfrac{\sqrt{3}}{2} \hat{\mathbf j}. \end{align*}\]

Ця цифра являє собою одиничну окружність. Це коло, зосереджене на початку. Він має вектор з початковою точкою на початку та кінцевою точкою на колі. Кінцева точка маркується (cos (theta), sin (theta)). Довжина вектора дорівнює 1 одиниці. Існує також прямокутний трикутник, утворений вектором як гіпотенуза. Горизонтальна сторона позначена «cos (theta)», а вертикальна сторона - «sin (theta)». — Малюнок$\PageIndex{19}$: Кінцева точка$\vecs{u}$ лежить на одиничному колі$(\cos θ, \sin θ)$.

Вправа$\PageIndex{8}$

Дозволяти$\vecs{a}=⟨16,−11⟩$ і нехай$\vecs{b}$ бути одиничний вектор, який утворює кут$225°$ з позитивним$x$ -вісь. Експрес$\vecs{a}$ і$\vecs{b}$ в терміні стандартних одиничних векторів.

Підказка: Використовуйте синус і косинус, щоб знайти компоненти$\vecs{b}$.
Відповідь: $\vecs{a}=16 \hat{\mathbf i}−11 \hat{\mathbf j}, \quad \vecs{b}=−\dfrac{\sqrt{2}}{2} \hat{\mathbf i}−\dfrac{\sqrt{2}}{2} \hat{\mathbf j}$

Застосування векторів

Оскільки вектори мають як напрямок, так і величину, вони є цінними інструментами для вирішення проблем, пов'язаних з такими додатками, як рух і сила. Згадаймо приклад човна і приклад захисника, який ми описали раніше. Тут ми детально розглянемо два інших приклади.

Приклад$\PageIndex{9A}$: Finding Resultant Force

Машина Джейн застрягла в бруді. Ліза і Джед приїжджають у вантажівці, щоб допомогти витягнути її. Вони прикріплюють один кінець буксирного ременя до передньої частини автомобіля, а інший кінець - до причіпного пристрою вантажівки, і вантажівка починає тягнути. Тим часом Джейн і Джед сідають за машину і штовхають. Вантажівка генерує горизонтальну силу 300 фунтів на автомобіль. Джейн і Джед штовхають під невеликим кутом вгору і генерують силу 150 фунтів на автомобіль. Ці сили можуть бути представлені векторами, як показано на малюнку$\PageIndex{20}$. Кут між цими векторами дорівнює 15°. Знайдіть результуючу силу (суму вектора) і дайте її величину до найближчої десятої частини фунта і кута її напрямку від позитивної$x$ -осі.

Це зображення є видом збоку автомобіля. З передньої частини автомобіля є горизонтальний вектор з написом «300 фунтів». Також з передньої частини автомобіля є ще один вектор з написом «150 фунтів». Кут між двома векторами становить 15 градусів. — Малюнок$\PageIndex{20}$: Дві сили, що діють на автомобіль в різні боки.

Рішення

Щоб знайти ефект об'єднання двох сил, додайте їх репрезентативні вектори. По-перше, висловіть кожен вектор в складовій формі або через стандартні одиничні вектори. Для цього найпростіше, якщо вирівняти один з векторів з позитивною$x$ -віссю. Тоді горизонтальний вектор має початкову точку$(0,0)$ та кінцеву точку$(300,0)$. Вона може виражатися як$⟨300,0⟩$ або$300 \hat{\mathbf i}$.

Другий вектор має величину$150$ і робить кут$15°$ з першим, тому ми можемо висловити його як$⟨150 \cos(15°),150 \sin(15°)⟩,$ або$150 \cos(15°)\hat{\mathbf i}+150 \sin(15°)\hat{\mathbf j}$. Тоді сума векторів, або результуючий вектор, є$\vecs{r}=⟨300,0⟩+⟨150 \cos(15°),150 \sin(15°)⟩,$ і ми маємо

\[\|\vecs{r}\|=\sqrt{(300+150 \cos(15°))^2+(150 \sin(15°))^2}≈446.6. \nonumber \]

Кут,$θ$ зроблений$\vecs{r}$ і позитивний$x$ -вісь має$\tan θ=\dfrac{150 \sin 15°}{(300+150\cos 15°)}≈0.09$, так$θ≈ \tan^{−1}(0.09)≈5°$, що означає, що результуюча сила$\vecs{r}$ має кут$5°$ вище горизонтальної осі.

Приклад$\PageIndex{9B}$: Finding Resultant Velocity

Літак летить через захід зі швидкістю повітря$425$ миль/год. Вітер дме з північного сходу на$40$ милі/год. Яка наземна швидкість літака? Що таке підшипник літака?

Рішення

Почнемо з ескізу описаної ситуації (рис.$\PageIndex{21}$).

Ця цифра є зображенням літака. Виходимо з передньої частини літака два вектори. Перший вектор має маркування «425», а другий вектор - «40». Кут між векторами дорівнює 45 градусів. — Малюнок$\PageIndex{21}$: Спочатку літак рухається через захід. Вітер з північного сходу, тому дме на південний захід. Кут між курсом площини і вітром дорівнює$45°$. (Малюнок не намальований в масштабі.)

Налаштуйте ескіз так, щоб початкові точки векторів лежали біля початку. Потім вектор швидкості площини є$\vecs{p}=−425\hat{\mathbf i}$. Вектор, що описує вітер, робить кут з$225°$ додатною$x$ -віссю:

\[\vecs{w}=⟨40 \cos(225°),40 \sin(225°)⟩=⟨−\dfrac{40}{\sqrt{2}},−\dfrac{40}{\sqrt{2}}⟩=−\dfrac{40}{\sqrt{2}}\hat{\mathbf i}−\dfrac{40}{\sqrt{2}}\hat{\mathbf j}. \nonumber \]

Коли швидкість повітря і вітер діють разом на площині, ми можемо додати їх вектори, щоб знайти результуючу силу:

\[\vecs{p}+\vecs{w}=−425\hat{\mathbf i}+(−\dfrac{40}{\sqrt{2}}\hat{\mathbf i}−\dfrac{40}{\sqrt{2}}\hat{\mathbf j})=(−425−\dfrac{40}{\sqrt{2}})\hat{\mathbf i}−\dfrac{40}{\sqrt{2}}\hat{\mathbf j}. \nonumber \]

Величина результуючого вектора показує вплив вітру на наземну швидкість літака:

$\|\vecs{p}+\vecs{w}\|=\sqrt{(−425−\dfrac{40}{\sqrt{2}})^2+(−\dfrac{40}{\sqrt{2}})^2}≈454.17$миль/год

В результаті вітру літак рухається приблизно зі швидкістю$454$ миль/год щодо землі.

Щоб визначити підшипник літака, хочемо знайти напрямок вектора$\vecs{p}+\vecs{w}$:

$\tan θ=\dfrac{−\dfrac{40}{\sqrt{2}}}{(−425−\dfrac{40}{\sqrt{2}})}≈0.06$

$θ≈3.57°$.

Загальний напрямок літака знаходиться на$3.57°$ південь від заходу.

Вправа$\PageIndex{9}$

Літак летить через північ зі швидкістю польоту$550$ миль/год. Вітер дме з північного заходу на$50$ милі/год. Яка наземна швидкість літака?

Підказка: Намалюйте вектори з однаковою початковою точкою і знайдіть їх суму.
Відповідь: Приблизно$516$ миль/год

Ключові поняття

Вектори використовуються для представлення величин, які мають як величину, так і напрямок.
Ми можемо додати вектори за допомогою методу паралелограма або методу трикутника, щоб знайти суму. Ми можемо помножити вектор на скаляр, щоб змінити його довжину або дати йому протилежний напрямок.
Віднімання векторів визначено в терміні додавання негативу вектора.
Вектор записується у вигляді компонента як$\vecs{v}=⟨x,y⟩$.
Величина вектора скалярна:$‖\vecs{v}‖=\sqrt{x^2+y^2}$.
Одиничний вектор$\vecs{u}$ має величину$1$ і його можна знайти шляхом ділення вектора на його величину:$\vecs{u}=\dfrac{1}{‖\vecs{v}‖}\vecs{v}$. Стандартними одиничними векторами є$\hat{\mathbf i}=⟨1,0⟩$ і$\hat{\mathbf j}=⟨0,1⟩$. Вектор$\vecs{v}=⟨x,y⟩$ може бути виражений через стандартні одиничні вектори як$\vecs{v}=x\hat{\mathbf i}+y\hat{\mathbf j}$.
Вектори часто використовуються у фізиці та техніці для представлення сил та швидкостей, серед інших величин.

Глосарій

складова: скаляр, який описує вертикальний або горизонтальний напрямок вектора

еквівалентні вектори: вектори, які мають однакову величину і однаковий напрямок

початкова точка: початкова точка вектора

величина: довжина вектора

нормалізація: використовуючи скалярне множення, щоб знайти одиничний вектор із заданим напрямком

метод паралелограма: метод знаходження суми двох векторів; розташувати вектори так, щоб вони поділяли одну і ту ж початкову точку; вектори потім утворюють дві сусідні сторони паралелограма; сума векторів - діагональ цього паралелограма

скалярний: дійсне число

скалярне множення: векторна операція, яка визначає добуток скаляра і вектора

вектор стандартного положення: вектор з початковою точкою$(0,0)$

стандартні одиничні вектори: одиничні вектори по осях координат:$\hat{\mathbf i}=⟨1,0⟩,\, \hat{\mathbf j}=⟨0,1⟩$

термінальна точка: кінцева точка вектора

нерівність трикутника: довжина будь-якої сторони трикутника менше суми довжин двох інших сторін

метод трикутника: метод знаходження суми двох векторів; розташуйте вектори так, що кінцева точка одного вектора є початковою точкою іншого; ці вектори потім утворюють дві сторони трикутника; сума векторів - вектор, який утворює третю сторону; початкова точка суми - початкова точка першої вектор; кінцева точка суми - кінцева точка другого вектора

одиниця вектор: вектор з величиною$1$

вектор: математичний об'єкт, який має як величину, так і напрямок

векторне додавання: векторна операція, яка визначає суму двох векторів

векторна різниця: різниця$\vecs{v}−\vecs{w}$ векторів визначається як$\vecs{v}+(−\vecs{w})=\vecs{v}+(−1)\vecs{w}$

векторна сума: сума двох векторів,$\vecs{v}$ і$\vecs{w}$, може бути побудована графічно, розмістивши початкову точку$\vecs{w}$ в кінцевій точці$\vecs{v}$; тоді векторна сума$\vecs{v}+\vecs{w}$ є вектор з початковою точкою, яка збігається з початковою точкою$\vecs{v}$, і з кінцевою точкою що збігається з кінцевою точкою$\vecs{w}$

нульовий вектор: вектор як з початковою точкою, так і кінцевою точкою$(0,0)$

Визначення: Еквівалентні вектори

Приклад\(\PageIndex{1}\): Sketching Vectors

Вправа\(\PageIndex{1}\)

Визначення: Скалярне множення

Визначення: Векторне додавання

Приклад\(\PageIndex{2}\): Combining Vectors

Вправа\(\PageIndex{2}\)

Приклад\(\PageIndex{3}\): Comparing Vectors

Вправа\(\PageIndex{3}\)

Визначення: Векторні компоненти

Правило: Компонентна форма вектора

Приклад\(\PageIndex{4}\): Expressing Vectors in Component Form

Вправа\(\PageIndex{4}\)

Визначення: Скалярне множення та додавання векторів

Приклад\(\PageIndex{5}\): Performing Operations in Component Form

Вправа\(\PageIndex{5A}\)

Властивості векторних операцій

Доказ Комутативного майна

Доказ розподільної власності

Вправа\(\PageIndex{5B}\)

Приклад\(\PageIndex{6}\): Finding the Component Form of a Vector Using Trigonometry

Вправа\(\PageIndex{6}\)

Приклад\(\PageIndex{7}\): Finding a Unit Vector

Вправа\(\PageIndex{7}\)

Приклад\(\PageIndex{8}\): Using Standard Unit Vectors

Вправа\(\PageIndex{8}\)

Приклад\(\PageIndex{9A}\): Finding Resultant Force

Приклад\(\PageIndex{9B}\): Finding Resultant Velocity

Вправа\(\PageIndex{9}\)