10.4: Робота з серією Тейлора
- Page ID
- 61553
- Напишіть терміни біноміального ряду.
- Розпізнайте розширення серії Тейлора загальних функцій.
- Розпізнайте та застосовуйте методи, щоб знайти серію Тейлора для функції.
- Використовуйте ряд Тейлора для вирішення диференціальних рівнянь.
- Використовуйте ряди Тейлора для оцінки неелементарних інтегралів.
У попередньому розділі ми визначили ряд Тейлора і показали, як знайти ряд Тейлора для декількох спільних функцій шляхом явного обчислення коефіцієнтів поліномів Тейлора. У цьому розділі ми показуємо, як використовувати ці серії Тейлора для отримання серії Тейлора для інших функцій. Потім ми представляємо два загальних застосування силових рядів. Спочатку ми покажемо, як силові ряди можуть бути використані для розв'язання диференціальних рівнянь. По-друге, показано, як степеневі ряди можуть бути використані для оцінки інтегралів, коли антипохідне цілого не може бути виражено термінами елементарних функцій. В одному прикладі ми розглянемо\(\displaystyle \int e^{−x^2}dx,\) інтеграл, який часто виникає в теорії ймовірностей.
Біноміальна серія
Наша перша мета в цьому розділі - визначити ряд Маклорена для функції\( f(x)=(1+x)^r\) для всіх дійсних чисел\( r\). Серія Маклорена для цієї функції відома як біноміальний ряд. Почнемо з розгляду найпростішого випадку:\( r\) це невід'ємне ціле число. Нагадаємо, що, для\( r=0,\,1,\,2,\,3,\,4,\;f(x)=(1+x)^r\) можна записати як
\[\begin{align*} f(x) &=(1+x)^0=1, \\[4pt] f(x) &=(1+x)^1=1+x, \\[4pt] f(x) &=(1+x)^2=1+2x+x^2, \\[4pt] f(x) &=(1+x)^3=1+3x+3x^2+x^3 \\[4pt] f(x) &=(1+x)^4=1+4x+6x^2+4x^3+x^4. \end{align*}\]
Вирази з правого боку відомі як біноміальні розширення, а коефіцієнти відомі як біноміальні коефіцієнти. Більш загально, для будь-якого\( r\) невід'ємного цілого числа біноміальний коефіцієнт\( x^n\) у біноміальному розширенні\( (1+x)^r\) задається
\[\binom{r}{n}=\dfrac{r!}{n!(r−n)!}\label{eq6.6} \]
і
\ [\ почати {вирівняти} f (x) &= (1+x) ^r\ nonumber\\ [5pt]
&=\ біном {r} {0} +\ біном {r} {1} x+\ binom {r} {2} x^2+\ binom {r} {3} x^3++\ binom {r} {r-1} x^2+ r−1} +\ біном {r} {r} x^r\ nonumber\\ [5pt]
&=\ сума {n=0} ^r\ binom {r} {n} x^n.\ мітка {eq6.7}\ кінець {вирівнювання}\]
Наприклад, використовуючи цю формулу для\( r=5\), ми бачимо, що
\[ \begin{align*} f(x) &=(1+x)^5 \\[4pt] &=\binom{5}{0}1+\binom{5}{1}x+\binom{5}{2}x^2+\binom{5}{3}x^3+\binom{5}{4}x^4+\binom{5}{5}x^5 \\[4pt] &=\dfrac{5!}{0!5!}1+\dfrac{5!}{1!4!}x+\dfrac{5!}{2!3!}x^2+\dfrac{5!}{3!2!}x^3+\dfrac{5!}{4!1!}x^4+\dfrac{5!}{5!0!}x^5 \\[4pt] &=1+5x+10x^2+10x^3+5x^4+x^5. \end{align*}\]
Розглянемо тепер випадок, коли показник\(r.\)
будь-яке дійсне число, не обов'язково невід'ємне ціле число. Якщо не\(r\) є невід'ємним цілим числом, то\(f(x)=(1+x)^r\) не можна записати як скінченний многочлен. Однак ми можемо знайти серію потужності для\(f\). Зокрема, ми шукаємо серію Maclaurin для\(f\). Для цього знаходимо похідні\(f\) і оцінюємо їх за адресою\(x=0\).
\[ \begin{align*} f(x) &=(1+x)^r & f(0) &=1 \\[4pt] f′(x) &=r(1+x)^{r−1} & f'(0) &=r \\[4pt] f''(x) &=r(r−1)(1+x)^{r−2} & f''(0) &=r(r−1) \\[4pt] f'''(x) &=r(r−1)(r−2)(1+x)^{r−3} & f'''(0) &=r(r−1)(r−2) \\[4pt] f^{(n)}(x) &=r(r−1)(r−2)⋯(r−n+1)(1+x)^{r−n} & f^{(n)}(0) &=r(r−1)(r−2)⋯(r−n+1) \end{align*}\]
Зроблено висновок, що коефіцієнти в біноміальному ряду задаються
\[\dfrac{f^{(n)}(0)}{n!}=\dfrac{r(r−1)(r−2)⋯(r−n+1)}{n!}.\label{eq6.8} \]
Відзначимо,\(r\) що якщо невід'ємне ціле число,\( f^{(r+1)}\) то\((r+1)^{\text{st}}\) похідна - нульова функція, а ряд закінчується. Крім того, якщо\( r\) невід'ємне ціле число, то Equation\ ref {eq6.8} для коефіцієнтів узгоджується з Equation\ ref {eq6.6} для коефіцієнтів, а формула для біноміального ряду узгоджується з Equation\ ref {eq6.7} для скінченного біноміального розширення. Якщо говорити більш загально, для позначення біноміальних коефіцієнтів для будь-якого дійсного числа\( r\) визначимо
\[\binom{r}{n}=\dfrac{(r−1)(r−2)⋯(r−n+1)}{n!}. \nonumber \]
За допомогою цього позначення ми можемо записати біноміальний ряд для\( (1+x)^r\) як
\[\sum_{n=0}^∞\binom{r}{n}x^n=1+rx+\dfrac{r(r−1)}{2!}x^2+⋯+\dfrac{r(r−1)⋯(r−n+1)}{n!}x^n+⋯. \label{bin1} \]
Тепер потрібно визначити інтервал збіжності для біноміального ряду Equation\ ref {bin1}. Наносимо тест співвідношення. Отже, ми вважаємо
\[\begin{align*} \dfrac{|a_{n+1}|}{|a_n|} &=\dfrac{|r(r−1)(r−2)⋯(r−n)|x||^{n+1}}{(n+1)!}⋅\dfrac{n}{|r(r−1)(r−2)⋯(r−n+1)||x|^n} \\[4pt] &=\dfrac{|r−n||x|}{|n+1|} \end{align*}\].
Так як
\[\lim_{n→∞}\dfrac{|a_{n+1}|}{|a_n|}=|x|<1 \nonumber \]
якщо і тільки якщо\( |x|<1\), робимо висновок, що інтервал збіжності для біноміального ряду дорівнює\( (−1,1)\). Поведінка на кінцевих точках залежить від\( r\). Можна показати, що для\( r≥0\) ряду сходиться в обох кінцевих точках; бо\( −1<r<0\), серія сходиться в\( x=1\) і розходиться в\( x=−1\); і для\( r<−1\), серія розходиться в обох кінцевих точках. Біноміальний ряд дійсно сходиться\( (1+x)^r\) в\( (−1,1)\) для всіх дійсних чисел\( r\), але довести цей факт, показуючи, що залишок\( R_n(x)→0\) важко.
Для будь-якого дійсного числа ряд\( r\) Маклорена для\( f(x)=(1+x)^r\) є біноміальним рядом. Він сходиться до\( f\) for\( |x|<1\), і ми пишемо
\[(1+x)^r=\sum_{n=0}^∞\binom{r}{n}x^n=1+rx+\dfrac{r(r−1)}{2!}x^2+⋯+r\dfrac{(r−1)⋯(r−n+1)}{n!}x^n+⋯ \nonumber \]
для\( |x|<1\).
Ми можемо використовувати це визначення, щоб знайти біноміальний ряд для\( f(x)=\sqrt{1+x}\) і використовувати ряд для наближення\( \sqrt{1.5}\).
- Знайдіть біноміальний ряд для\( f(x)=\sqrt{1+x}\).
- Використовуйте многочлен Маклорена третього порядку\( p_3(x)\) для оцінки\( \sqrt{1.5}\). Використовуйте теорему Тейлора, щоб зв'язати помилку. Використовуйте утиліту графіків для порівняння графіків\( f\) і\( p_3\).
Рішення
а. тут\( r=\dfrac{1}{2}\). Використовуючи визначення для біноміального ряду, отримаємо
\ (\ стиль відображення\ qquad\ почати {вирівнювати*}\ sqrt {1+x} &=1+\ dfrac {1} {2} x+\ dfrac {(1/2) (−1/2)} {2!} x^2+\ dfrac {(1/2) (−1/2) (−3/2)} {3!} x^3+\\ [5pt]
&=1+\ dfrac {1} {2} x−\ dfrac {1} {2!} \ dfrac {1} {2^2} x^2+\ dfrac {1} {3!} \ dfrac {1⋅3} {2^3} x^3−+\ dfrac {(−1) ^ {n+1}} {n!} \ dfrac {1⋅3⋅5( 2n−3)} {2^n} x^n+\\ [5pt]
&=1+\ sum_ {n=1} ^∞\ dfrac {(−1) ^ {n+1}} {n!} \ dfrac {1⋅3⋅5( 2n−3)} {2^n} x^n.\ end {align*}\)
b. з результату в частині a. поліном Маклорена третього порядку дорівнює
\( p_3(x)=1+\dfrac{1}{2}x−\dfrac{1}{8}x^2+\dfrac{1}{16}x^3\).
Тому,
\( \sqrt{1.5}=\sqrt{1+0.5}≈1+\dfrac{1}{2}(0.5)−\dfrac{1}{8}(0.5)^2+\dfrac{1}{16}(0.5)^3≈1.2266.\)
З теореми Тейлора помилка задовольняє
\( R_3(0.5)=\dfrac{f^{(4)}(c)}{4!}(0.5)^4\)
для деяких\( c\) між\( 0\) і\( 0.5\). Так як\( f^{(4)}(x)=−\dfrac{15}{2^4(1+x)^{7/2}}\), і максимальне значення\( ∣f^{(4)}(x)∣\) на інтервалі\( (0,0.5)\) відбувається в\( x=0\), ми маємо
\( |R_3(0.5)|≤\dfrac{15}{4!2^4}(0.5)^4≈0.00244.\)
Функція та многочлен Маклорена\( p_3\) зображені на малюнку\(\PageIndex{1}\).
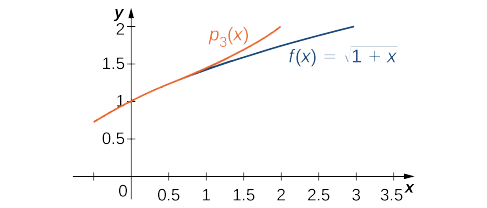
Знайдіть біноміальний ряд для\( f(x)=\dfrac{1}{(1+x)^2}\).
- Підказка
-
Використовуйте визначення біноміальних рядів для\( r=−2\).
- Відповідь
-
\(\displaystyle \sum_{n=0}^∞(−1)^n(n+1)x^n\)
Загальні функції, виражені як серія Тейлора
На цьому етапі ми вивели ряд Маклорена для експоненціальних, тригонометричних та логарифмічних функцій, а також функцій виду\( f(x)=(1+x)^r\). У\(\PageIndex{1}\) табл підсумовуємо результати цих рядів. Зауважимо, що збіжність ряду Маклорена для\( f(x)=\ln(1+x)\) кінцевої точки\( x=1\) та ряду Маклорена для\( f(x)=\tan^{−1}x\) в кінцевих точках\( x=1\) і\( x=−1\) спирається на більш просунуту теорему, ніж ми представляємо тут. (Зверніться до теореми Абеля для обговорення цього більш технічного моменту.)
| Функція | Серія Маклорен | Інтервал збіжності |
|---|---|---|
| \( f(x)=\dfrac{1}{1−x}\) | \(\displaystyle \sum_{n=0}^∞x^n\) | \( −1<x<1\) |
| \( f(x)=e^x\) | \(\displaystyle \sum_{n=0}^∞\dfrac{x^n}{n!}\) | \( −∞<x<∞\) |
| \( f(x)=\sin x\) | \(\displaystyle \sum_{n=0}^∞(−1)^n\dfrac{x^{2n+1}}{(2n+1)!}\) | \( −∞<x<∞\) |
| \( f(x)=\cos x\) | \(\displaystyle \sum_{n=0}^∞(−1)^n\dfrac{x^{2n}}{(2n)!}\) | \( −∞<x<∞\) |
| \( f(x)=\ln(1+x)\) | \(\displaystyle \sum_{n=0}^∞(−1)^{n+1}\dfrac{x^n}{n}\) | \( −1<x<1\) |
| \( f(x)=\tan^{−1}x\) | \(\displaystyle \sum_{n=0}^∞(−1)^n\dfrac{x^{2n+1}}{2n+1}\) | \( −1<x<1\) |
| \( f(x)=(1+x)^r\) | \(\displaystyle \sum_{n=0}^∞\binom{r}{n}x^n\) | \( −1<x<1\) |
Раніше в розділі ми показали, як можна поєднувати силові ряди для створення нових силових рядів. Тут ми використовуємо ці властивості в поєднанні з серією Маклорена в таблиці\(\PageIndex{1}\), щоб створити ряд Маклорена для інших функцій.
Знайдіть ряд Маклорена кожної з наступних функцій, скориставшись однією з рядів, зазначених у табл\(\PageIndex{1}\).
- \( f(x)=\cos\sqrt{x}\)
- \( f(x)=\sinh x\)
Рішення
а Використовуючи серію Маклорена,\( \cos x\) ми знаходимо, що серія\( \cos\sqrt{x}\) Маклорена для дається
\(\displaystyle \sum_{n=0}^∞\dfrac{(−1)^n(\sqrt{x})^{2n}}{(2n)!}=\sum_{n=0}^∞\dfrac{(−1)^nx^n}{(2n)!}=1−\dfrac{x}{2!}+\dfrac{x^2}{4!}−\dfrac{x^3}{6!}+\dfrac{x^4}{8!}−⋯.\)
Цей ряд сходиться до\( \cos\sqrt{x}\) для всіх\( x\) в області\( \cos\sqrt{x}\); тобто для всіх\( x≥0\).
б. для пошуку серії Маклорена\( \sinh x,\) ми використовуємо той факт, що
\( \sinh x=\dfrac{e^x−e^{−x}}{2}.\)
Використовуючи ряд Маклорена для\( e^x\), ми бачимо, що\(n^{\text{th}}\) термін у серії Маклорена для\(\sinh x\) дається
\( \dfrac{x^n}{n!}−\dfrac{(−x)^n}{n!}.\)
Для\( n\) парних цей термін дорівнює нулю. Для\( n\) непарних цей термін є\( \dfrac{2x^n}{n!}\). Тому серія Maclaurin for\(\sinh x\) має лише умови непарного порядку і дається
\(\displaystyle \sum_{n=0}^∞\dfrac{x^{2n+1}}{(2n+1)!}=x+\dfrac{x^3}{3!}+\dfrac{x^5}{5!}+⋯.\)
Знайдіть серію Маклорена для\( \sin(x^2).\)
- Підказка
-
Використовуйте серію Maclaurin для\( \sin x.\)
- Відповідь
-
\(\displaystyle \sum_{n=0}^∞\dfrac{(−1)^nx^{4n+2}}{(2n+1)!}\)
Ми також показали раніше в цьому розділі, як силові ряди можна диференціювати термін за терміном для створення нового силового ряду. У прикладі\(\PageIndex{3}\) ми розмежовуємо біноміальні ряди для\( \sqrt{1+x}\) терміну за терміном, щоб знайти біноміальний ряд для\( \dfrac{1}{\sqrt{1+x}}\). Зауважте, що ми могли б побудувати біноміальний ряд для\( \dfrac{1}{\sqrt{1+x}}\) безпосередньо з визначення, але диференціювання біноміальних рядів для\( \sqrt{1+x}\) є простішим обчисленням.
Використовуйте біноміальний ряд for,\( \sqrt{1+x}\) щоб знайти біноміальний ряд для\( \dfrac{1}{\sqrt{1+x}}\).
Рішення
Дві функції пов'язані
\( \dfrac{d}{dx}\sqrt{1+x}=\dfrac{1}{2\sqrt{1+x}}\),
тому біноміальний ряд для\( \dfrac{1}{\sqrt{1+x}}\) задається
\(\displaystyle \dfrac{1}{\sqrt{1+x}}=2\dfrac{d}{dx}\sqrt{1+x}=1+\sum_{n=1}^∞\dfrac{(−1)^n}{n!}\dfrac{1⋅3⋅5⋯(2n−1)}{2^n}x^n.\)
Знайдіть біноміальний ряд для\( f(x)=\dfrac{1}{(1+x)^{3/2}}\)
- Підказка
-
Диференціювати серію для\( \dfrac{1}{\sqrt{1+x}}\)
- Відповідь
-
\(\displaystyle \sum_{n=1}^∞\dfrac{(−1)^n}{n!}\dfrac{1⋅3⋅5⋯(2n−1)}{2^n}x^n\)
У цьому прикладі ми диференціювали відомий ряд Тейлора для побудови ряду Тейлора для іншої функції. Здатність диференціювати степеневі ряди за терміном робить їх потужним інструментом для розв'язання диференціальних рівнянь. Зараз ми покажемо, як це досягається.
Розв'язування диференціальних рівнянь з степен
Розглянемо диференціальне рівняння
\[y′(x)=y.\nonumber \]
Нагадаємо, що це роздільне рівняння першого порядку і його рішення є\(y=Ce^x\). Це рівняння легко вирішується за допомогою методів, розглянутих раніше в тексті. Однак для більшості диференціальних рівнянь ми ще не маємо аналітичних інструментів для їх вирішення. Силові ряди є надзвичайно корисним інструментом для вирішення багатьох типів диференціальних рівнянь. У цій техніці шукаємо рішення форми\(\displaystyle y=\sum_{n=0}^∞c_nx^n\) і визначаємо, які коефіцієнти повинні бути. У наступному прикладі ми розглянемо початково-вартісну задачу, яка передбачає\(y′=y\) ілюстрацію методики.
Використовуйте серію потужності для вирішення проблеми початкового значення\(y′=y,\quad y(0)=3.\)
Рішення
Припустимо, що існує рішення силового ряду
\(\displaystyle y(x)=\sum_{n=0}^∞c_nx^n=c_0+c_1x+c_2x^2+c_3x^3+c_4x^4+⋯.\)
Диференціюючи цей термін ряду за терміном, отримаємо
\( y′=c_1+2c_2x+3c_3x^2+4c_4x^3+⋯.\)
Якщо\(y\) задовольняє диференціальне рівняння, то
\( c_0+c_1x+c_2x^2+c_3x^3+⋯=c_1+2c_2x+3c_3x^2+4c_3x^3+⋯.\)
Використовуючи унікальність уявлень степеневих рядів, ми знаємо, що ці ряди можуть бути рівними тільки в тому випадку, якщо їх коефіцієнти рівні. Тому,
\( c_0=c_1,\)
\( c_1=2c_2,\)
\( c_2=3c_3,\)
\( c_3=4c_4,\)
⋮
Використання початкової умови,\( y(0)=3\) поєднаної з представленням степеневого ряду
\( y(x)=c_0+c_1x+c_2x^2+c_3x^3+⋯\),
ми знаходимо, що\( c_0=3\). Тепер ми готові вирішити для решти коефіцієнтів. Використовуючи те\( c_0=3\), що, ми маємо
\ [\ почати {вирівнювати*} c_1&=c_0=3=\ dfrac {3} {1!} ,\\ [5pt]
c_2&=\ dfrac {c_1} {2} =\ dfrac {3} {2} =\ dfrac {3} {2!} ,\\ [5pt]
c_3&=\ dfrac {c_2} {3} =\ dfrac {3} {3⋅2} =\ dfrac {3} {3!} ,\\ [5pt]
c_4&=\ dfrac {c_3} {4} =\ dfrac {3} {4⋅3⋅2} =\ dfrac {3} {4!}. \ end {вирівнювати*}\]
Тому,
\[y=3\left[1+\dfrac{1}{1!}x+\dfrac{1}{2!}x^2+\dfrac{1}{3!}x^3\dfrac{1}{4!}x^4+⋯\right]=3\sum_{n=0}^∞\dfrac{x^n}{n!}.\nonumber \]
Ви можете розпізнати
\[\sum_{n=0}^∞\dfrac{x^n}{n!}\nonumber \]
як серіал Тейлора для\( e^x\). Тому рішення є\( y=3e^x\).
Використовуйте серію живлення для вирішення\( y′=2y,\quad y(0)=5.\)
- Підказка
-
Рівняння для перших кількох коефіцієнтів\( c_n\) задовольнять\( c_0=2c_1,\,c_1=2⋅2c_2,\,c_2=2⋅3c_3,\,….\) Загалом, для всіх\( n≥0,\;c_n=2(n+1)C_{n+1}\).
- Відповідь
-
\( y=5e^{2x}\)
Зараз ми розглянемо приклад із застосуванням диференціального рівняння, яке ми не можемо вирішити за допомогою раніше розглянутих методів. Це диференціальне рівняння
\[y′−xy=0\nonumber \]
відомий як рівняння Ейрі. Він має багато застосувань у математичній фізиці, таких як моделювання дифракції світла. Тут ми покажемо, як вирішити це за допомогою силових рядів.
Використовуйте серію потужності для вирішення\(y''−xy=0\) з початковими умовами\( y(0)=a\) та\( y'(0)=b.\)
Рішення
Шукаємо рішення форми
\[y=\sum_{n=0}^∞c_nx^n=c_0+c_1x+c_2x^2+c_3x^3+c_4x^4+⋯\nonumber \]
Диференціюючи цей термін функції за терміном, отримаємо
\ [\ почати {align*} y′&=c_1+2c_2x+3c_3x^2+4c_4x^3+,\\ [4pt]
y"&=2⋅1c_2+3⋅2c_3x+4⋅3c_3c_4x_4x^2+. \ end {вирівнювати*}\]
Якщо рівняння\(y\) задовольняє\( y''=xy\), то
\( 2⋅1c_2+3⋅2c_3x+4⋅3c_4x^2+⋯=x(c_0+c_1x+c_2x^2+c_3x^3+⋯).\)
Використовуючи [посилання] на єдиність уявлень степеневих рядів, ми знаємо, що коефіцієнти одного ступеня повинні бути рівними. Тому,
\( 2⋅1c_2=0,\)
\( 3⋅2c_3=c_0,\)
\( 4⋅3c_4=c_1,\)
\( 5⋅4c_5=c_2,\)
⋮
У загальному плані, для\( n≥3\), у нас є\( n⋅(n−1)c_n=c_{n−3}\). По суті, всі коефіцієнти можна записати в терміні\( c_0\) і\( c_1\). Щоб переконатися в цьому, спочатку зауважте, що\( c_2=0\). Тоді
\( c_3=\dfrac{c_0}{3⋅2}\),
\( c_4=\dfrac{c_1}{4⋅3}\).
Бо\( c_5,\,c_6,\,c_7\), ми бачимо, що
\ [\ почати {вирівнювати*} c_5&=\ dfrac {c_2} {5⋅4} =0,\\ [5pt]
c_6&=\ dfrac {c_3} {6⋅5} =\ dfrac {c_0} {6⋅5⋅3⋅2},\\ [5pt] c_7&=\ dfrac {c_0} {6⋅5⋅3},\\ [5pt]
c_7&=\ dfrac {c_0} {6⋅5⋅3}} {7⋅6} =\ dfrac {c_1} {7⋅6⋅4⋅3}. \ end {вирівнювати*}\]
Тому послідовне розв'язання диференціального рівняння задається
\( y=c_0+c_1x+0⋅x^2+\dfrac{c_0}{3⋅2}x^3+\dfrac{c_1}{4⋅3}x^4+0⋅x^5+\dfrac{c_0}{6⋅5⋅3⋅2}x^6+\dfrac{c_1}{7⋅6⋅4⋅3}x^7+⋯.\)
Початкова умова\( y(0)=a\) має на увазі\( c_0=a\). Диференціюючи цей термін ряду за терміном і використовуючи той факт\( y′(0)=b\), що, ми робимо висновок, що\( c_1=b\).
Тому розв'язання цієї початково-значущової задачі є
\( y=a\left(1+\dfrac{x^3}{3⋅2}+\dfrac{x}{6⋅5⋅3⋅2}+⋯\right)+b\left(x+\dfrac{x^4}{4⋅3}+\dfrac{x^7}{7⋅6⋅4⋅3}+⋯\right).\)
Використовуйте силові ряди для вирішення\( y''+x^2y=0\) з початковою умовою\( y(0)=a\) і\( y′(0)=b\).
- Підказка
-
Коефіцієнти задовольняють\( c_0=a,\,c_1=b,\,c_2=0,\,c_3=0,\) і за\( n≥4,\; n(n−1)c_n=−c_{n−4}\).
- Відповідь
-
\(y=a\left(1−\dfrac{x^4}{3⋅4}+\dfrac{x^8}{3⋅4⋅7⋅8}−⋯\right)+b\left(x−\dfrac{x^5}{4⋅5}+\dfrac{x^9}{4⋅5⋅8⋅9}−⋯\right)\)
Оцінка неелементарних інтегралів
Розв'язування диференціальних рівнянь є одним із поширених застосувань степеневих Тепер перейдемо до другого додатка. Показано, як степеневі ряди можуть бути використані для оцінки інтегралів за участю функцій, антипохідні яких неможливо виразити за допомогою елементарних функцій.
Один інтеграл, який часто виникає в додатках теорії ймовірностей, - це\(\displaystyle \int e^{−x^2}\,dx.\) На жаль, антипохідне цілісного не\( e^{−x^2}\) є елементарною функцією. Під елементарною функцією ми маємо на увазі функцію, яку можна записати за допомогою скінченного числа алгебраїчних комбінацій або композицій експоненціальних, логарифмічних, тригонометричних або степеневих функцій. Зауважимо, що термін «елементарна функція» не є синонімом нескладної функції. Наприклад, функція\( f(x)=\sqrt{x^2−3x}+e^{x^3}−\sin(5x+4)\) є елементарною функцією, хоча і не особливо простий на вигляд функцією. Будь-інтеграл форми,\(\displaystyle \int f(x)\,dx\) де\( f\) антипохідне не можна записати як елементарну функцію, вважається неелементарним інтегралом.
неелементарні інтеграли не можуть бути оцінені за допомогою основних методів інтеграції, розглянутих раніше. Одним із способів оцінки таких інтегралів є вираження integrand як степеневого ряду та інтеграції термін за терміном. Ми демонструємо цю техніку, розглядаючи\(\displaystyle \int e^{−x^2}\,dx.\)
- Експрес\(\displaystyle \int e^{−x^2}dx\) як нескінченний ряд.
- \(\displaystyle \int ^1_0e^{−x^2}dx\)Оцініть в межах помилки\( 0.01\).
Рішення
а. серія Маклорена для\( e^{−x^2}\) дається
\ [\ begin {вирівнювати*} e^ {−x^2} &=\ sum_ {n=0} ^∞\ dfrac {(−x^2) ^n} {n!} \\ [5pt]
&=1−x^2+\ dfrac {x^4} {2!} −\ dfrac {x^6} {3!} ++ (−1) ^n\ dfrac {x^ {2n}} {n!} +\\ [5pt]
&=\ сума_ {n=0} ^∞ (−1) ^n\ dfrac {x^ {2n}} {n!}. \ end {вирівнювати*}\]
Тому,
\ [\ begin {align*}\ int e^ {−x^2}\, dx&=\ int\ ліворуч (1−x^2+\ dfrac {x^4} {2!} −\ dfrac {x^6} {3!} ++ (−1) ^n\ dfrac {x^ {2n}} {n!} +\ праворуч)\, dx\\ [5pt]
&=C+x−\ dfrac {x^3} {3} +\ dfrac {x^5} {5.2!} −\ dfrac {x^7} {7.3!} ++ (−1) ^n\ dfrac {x^ {2n+1}} {(2n+1) n!} +. \ end {вирівнювати*}\]
b Використовуючи результат з частини a. ми маємо
\[ \int ^1_0e^{−x^2}\,dx=1−\dfrac{1}{3}+\dfrac{1}{10}−\dfrac{1}{42}+\dfrac{1}{216}−⋯.\nonumber \]
Сума перших чотирьох членів приблизно\( 0.74\). За допомогою тесту змінного ряду ця оцінка точна з точністю до похибки менше\( \dfrac{1}{216}≈0.0046296<0.01.\)
Експрес\(\displaystyle \int \cos\sqrt{x}\,dx\) як нескінченний ряд. \(\displaystyle \int ^1_0\cos\sqrt{x}\,dx\)Оцініть в межах помилки\( 0.01\).
- Підказка
-
Скористайтеся серіями, знайденими в\(\PageIndex{6}\) Прикладі.
- Відповідь
-
\(\displaystyle C+\sum_{n=1}^∞(−1)^{n+1}\dfrac{x^n}{n(2n−2)!}\)Певний інтеграл знаходиться приблизно\( 0.514\) в межах похибки\( 0.01\).
Як уже згадувалося вище, інтеграл\(\displaystyle \int e^{−x^2}\,dx\) виникає часто в теорії ймовірностей. Зокрема, він використовується при вивченні наборів даних, які зазвичай розподіляються, тобто значення даних лежать під кривою у формі дзвона. Наприклад, якщо набір значень даних нормально розподіляється із середнім\( μ\) і стандартним відхиленням\( σ\), то ймовірність того, що випадково вибране значення лежить між\( x=a\) і\( x=b\) задається
\[\dfrac{1}{σ\sqrt{2π}}\int ^b_ae^{−(x−μ)^2/(2σ^2)}\,dx.\label{probeq} \]
(Див\(\PageIndex{2}\). Рис.)
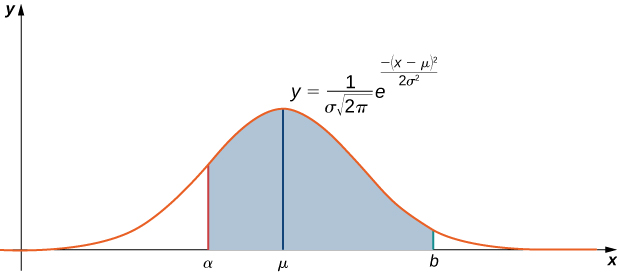
Щоб спростити цей інтеграл, ми, як правило, дозволяють\( z=\dfrac{x−μ}{σ}\). Ця величина\(z\) відома як\(z\) оцінка значення даних. З цим спрощенням інтегральне рівняння\ ref {probeq} стає
\[\dfrac{1}{\sqrt{2π}}\int ^{(b−μ)/σ}_{(a−μ)/σ}e^{−z^2/2}\,dz. \nonumber \]
У прикладі ми покажемо\(\PageIndex{7}\), як ми можемо використовувати цей інтеграл при обчисленні ймовірностей.
Припустимо, набір стандартизованих тестових балів зазвичай розподіляється із середнім\( μ=100\) і стандартним відхиленням\( σ=50\). Використовуйте Equation\ ref {probeq} та перші шість членів ряду Маклорена,\( e^{−x^2/2}\) щоб наблизити ймовірність того, що випадково вибраний тестовий бал знаходиться між\( x=100\) і\( x=200\). Використовуйте тест чергування рядів, щоб визначити, наскільки точним є ваше наближення.
Рішення
Оскільки\( μ=100,σ=50,\) і ми намагаємося визначити площу під кривою від\( a=100\) до\( b=200\), інтегральне рівняння\ ref {probeq} стає
\[ \dfrac{1}{\sqrt{2π}}\int ^2_0e^{−z^2/2}\,dz.\nonumber \]
Серія Маклорена для\( e^{−x^2/2}\) дається
\ [\ begin {align*} e^ {−x^2/2} &=\ sum_ {n=0} ^∞\ dfrac {\ ліворуч (−\ dfrac {x^2} {2}\ праворуч) ^n} {n!} \\ [5pt]
&=1−\ dfrac {x^2} {2^1⋅1!} +\ dfrac {x^4} {2^2⋅2!} −\ dfrac {x^6} {2^3⋅3!} ++ (−1) ^n\ dfrac {x^ {2n}} {2^n⋅n}! +\\ [5pt]
&=\ сума_ {n=0} ^∞ (−1) ^n\ dfrac {x^ {2n}} {2^n⋅n!}. \ end {вирівнювати*}\]
Тому,
\ [\ почати {вирівнювати*}\ dfrac {1} {\ sqrt {2π}}\ int e^ {−z^2/2}\, дз&=\ dfrac {1} {\ sqrt {2π}}\ int\ ліворуч (1−\ dfrac {z^2} {2^1⋅1!} +\ dfrac {z^4} {2^2⋅2!} −\ dfrac {z^6} {2^3⋅3!} ++ (−1) ^n\ dfrac {z^ {2n}} {2^n⋅n!} +\ праворуч) дз\\ [5пт]
&=\ dfrac {1} {\ sqrt {2π}}\ ліворуч (C+Z −\ dfrac {z^3} {3⋅2^1⋅1!} +\ dfrac {z^5} {5⋅2^2⋅2!} −\ dfrac {z^7} {7⋅2^3⋅3!} ++ (−1) ^n\ dfrac {z^ {2n+1}} {(2n+1) 2^n⋅n!} +\ праворуч)\ end {align*}\]
\[\dfrac{1}{\sqrt{2π}}\int ^2_0e^{−z^2/2}\,dz=\dfrac{1}{\sqrt{2π}}\left(2−\dfrac{8}{6}+\dfrac{32}{40}−\dfrac{128}{336}+\dfrac{512}{3456}−\dfrac{2^{11}}{11⋅2^5⋅5!}+⋯\right)\nonumber \]
Використовуючи перші п'ять членів, оцінюємо, що ймовірність становить приблизно 0,4922. За допомогою тесту на чергування рядів ми бачимо, що ця оцінка точна в межах
\[ \dfrac{1}{\sqrt{2π}}\dfrac{2^{13}}{13⋅2^6⋅6!}≈0.00546.\nonumber \]
Аналіз
Якщо ви знайомі з теорією ймовірностей, ви можете знати, що ймовірність того, що значення даних знаходиться в межах двох стандартних відхилень від середнього, приблизно.\( 95\%.\) Тут ми розрахували ймовірність того, що значення даних знаходиться між середнім і двома стандартними відхиленнями вище середнього, тому оцінка повинна бути навколо\( 47.5\%\). Кошторис в поєднанні з прив'язаною по точності потрапляє в цей діапазон.
Використовуйте перші п'ять термінів серії Маклорена для оцінки ймовірності\( e^{−x^2/2}\) того, що випадково обраний тестовий бал знаходиться між\( 100\) і\( 150\). Використовуйте тест чергуються рядів, щоб визначити точність цієї оцінки.
- Підказка
-
Оцініть,\(\displaystyle \int ^1_0e^{−z^2/2}\,dz\) використовуючи перші п'ять термінів серії Маклорен для\( e^{−z^2/2}\).
- Відповідь
-
Оцінка приблизно\( 0.3414.\) Ця оцінка точна з точністю до\( 0.0000094.\)
Ще одне застосування, при якому виникає неелементарний інтеграл, передбачає період маятника. Інтеграл - це
\[\int ^{π/2}_0\dfrac{dθ}{\sqrt{1−k^2\sin^2θ}}\nonumber \].
Інтеграл цієї форми відомий як еліптичний інтеграл першого роду. Еліптичні інтеграли спочатку виникли при спробі обчислити довжину дуги еліпса. Зараз ми покажемо, як використовувати силові ряди, щоб наблизити цей інтеграл.
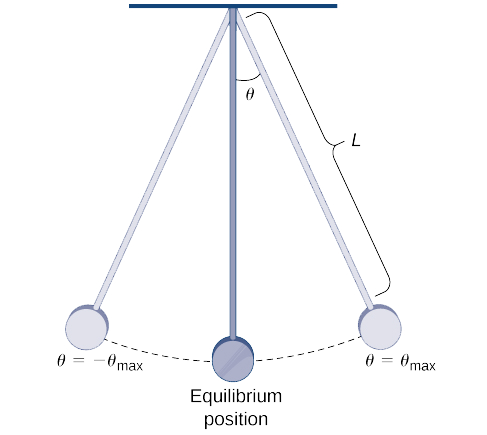
Період маятника - це час, необхідний для маятника, щоб зробити один повний поворот назад і вперед. Для маятника з довжиною\( L\), що робить максимальний кут\( θ_{max}\) з вертикаллю, його період\( T\) задається
\[ T=4\sqrt{\dfrac{L}{g}}\int ^{π/2}_0\dfrac{dθ}{\sqrt{1−k^2\sin^2θ}}\nonumber \]
де\( g\) - прискорення за рахунок сили тяжіння і\( k=\sin\left(\dfrac{θ_{max}}{2}\right)\) (див. Рис.\(\PageIndex{3}\)). (Відзначимо, що дана формула для періоду виникає з нелінеаризованої моделі маятника. У деяких випадках для спрощення використовується лінеаризована модель і\(\sin θ\) наближається по\( θ\).)
Використовуйте біноміальний ряд
\[ \dfrac{1}{\sqrt{1+x}}=1+\sum_{n=1}^∞\dfrac{(−1)^n}{n!}\dfrac{1⋅3⋅5⋯(2n−1)}{2^n}x^n\nonumber \]
оцінити період дії цього маятника. Зокрема, приблизний період маятника, якщо
- ви використовуєте лише перший термін у біноміальному ряді, і
- ви використовуєте перші два члени в біноміальному ряду.
Рішення
Ми використовуємо біноміальний ряд, замінюючи x на\( −k^2\sin^2θ.\) Тоді ми можемо записати період як
\[ T=4\sqrt{\dfrac{L}{g}}\int ^{π/2}_0\left(1+\dfrac{1}{2}k^2\sin^2θ+\dfrac{1⋅3}{2!2^2}k^4\sin^4θ+⋯\right)\,dθ.\nonumber \]
a Використовуючи лише перший термін у integrand, оцінка першого порядку
\[ T≈4\sqrt{\dfrac{L}{g}}\int ^{π/2}_0\,dθ=2π\sqrt{\dfrac{L}{g}}.\nonumber \]
Якщо\( θ_{max}\) маленька,\( k=\sin\left(\dfrac{θ_{max}}{2}\right)\) то маленька. Ми стверджуємо,\( k\) що коли мало, це хороша оцінка. Щоб обґрунтувати це твердження, розглянемо
\[ \int ^{π/2}_0\left(1+\frac{1}{2}k^2\sin^2θ+\dfrac{1⋅3}{2!2^2}k^4\sin^4θ+⋯\right)\,dθ.\nonumber \]
Так як\( |\sin x|≤1\), цей інтеграл обмежений
\[ \int ^{π/2}_0\left(\dfrac{1}{2}k^2+\dfrac{1.3}{2!2^2}k^4+⋯\right)\,dθ\;<\;\dfrac{π}{2}\left(\dfrac{1}{2}k^2+\dfrac{1⋅3}{2!2^2}k^4+⋯\right).\nonumber \]
Крім того, можна показати, що кожен коефіцієнт з правого боку менше, ніж\( 1\) і, отже, що цей вираз обмежений
\( \dfrac{πk^2}{2}(1+k^2+k^4+⋯)=\dfrac{πk^2}{2}⋅\dfrac{1}{1−k^2}\),
який невеликий для\( k\) малого.
б Для більших значень\( θ_{max}\), ми можемо наблизити,\( T\) використовуючи більше термінів в integrand. Використовуючи перші два члени в інтегралі, ми приходимо до оцінки
\[ T≈4\sqrt{\frac{L}{g}}\int ^{π/2}_0\left(1+\dfrac{1}{2}k^2\sin^2θ\right)\,dθ=2π\sqrt{\dfrac{L}{g}}\left(1+\dfrac{k^2}{4}\right).\nonumber \]
Застосування серії Тейлора в цьому розділі покликані підкреслити їх важливість. Загалом, ряди Тейлора корисні тим, що дозволяють нам представляти відомі функції за допомогою поліномів, тим самим надаючи нам інструмент для наближення значень функцій та оцінки складних інтегралів. Крім того, вони дозволяють визначити нові функції як ряди степенів, тим самим надаючи нам потужний інструмент для розв'язання диференціальних рівнянь.
Ключові поняття
- Біноміальний ряд - це серія Маклорена для\( f(x)=(1+x)^r\). Він сходиться для\( |x|<1\).
- Серія Тейлора для функцій часто може бути виведена алгебраїчними операціями з відомим рядом Тейлора або шляхом диференціації або інтеграції відомого ряду Тейлора.
- Силові ряди можуть бути використані для вирішення диференціальних рівнянь.
- Ряди Тейлора можуть бути використані для наближення інтегралів, які не можуть бути оцінені іншими засобами.
Глосарій
- біноміальний ряд
- серія Maclaurin для\( f(x)=(1+x)^r\); це дається\(\displaystyle (1+x)^r=\sum_{n=0}^∞\binom{r}{n}x^n=1+rx+\dfrac{r(r−1)}{2!}x^2+⋯+\dfrac{r(r−1)⋯(r−n+1)}{n!}x^n+⋯\) для\( |x|<1\)
- неелементарний інтеграл
- інтеграл, для якого антипохідне цілого не може бути виражено як елементарна функція
