10.1: Серія живлення та функції

Last updated
Save as PDF

Page ID: 61527

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Цілі навчання

Визначте силові ряди та наведіть їх приклади.
Визначте радіус збіжності та інтервал збіжності степеневого ряду.
Використовуйте силовий ряд для представлення функції.

Силовий ряд - це тип серії з термінами, що включають змінну. Більш конкретно, якщо змінна є$x$, то всі терміни ряду мають на увазі повноваження$x$. Як результат, степеневий ряд можна розглядати як нескінченний многочлен. Силові ряди використовуються для представлення загальних функцій, а також для визначення нових функцій. У цьому розділі ми визначаємо ряди потужності та покажемо, як визначити, коли силовий ряд сходиться і коли він розходиться. Ми також покажемо, як представляти певні функції за допомогою силових рядів.

Форма силового ряду

Серія форми

\[\sum_{n=0}^∞c_nx^n=c_0+c_1x+c_2x^2+\ldots , \nonumber \]

де$x$ змінна, а$c_n$ коефіцієнти - константи, відомий як силовий ряд. Серіал

\[1+x+x^2+\ldots =\sum_{n=0}^∞x^n \nonumber \]

є прикладом силового ряду. Оскільки цей ряд є геометричним рядом із співвідношенням$r=|x|$, ми знаємо, що він сходиться, якщо$|x|<1$ і розходиться, якщо$|x|≥1.$

Визначення$\PageIndex{1}$: Power Series

Серія форми

\[\sum_{n=0}^∞c_nx^n=c_0+c_1x+c_2x^2+\ldots \nonumber \]

це силовий ряд, зосереджений на серії$x=0.$ A форми

\[\sum_{n=0}^∞c_n(x−a)^n=c_0+c_1(x−a)+c_2(x−a)^2+\ldots \nonumber \]

це силовий ряд, зосереджений на$x=a$.

Щоб зробити це визначення точним, ми обумовимо, що$x^0=1$ і$(x−a)^0=1$ навіть коли$x=0$ і$x=a$, відповідно.

Серіал

\[\sum_{n=0}^∞\dfrac{x^n}{n!}=1+x+\dfrac{x^2}{2!}+\dfrac{x^3}{3!}+\ldots \nonumber \]

\[\sum_{n=0}^∞n!x^n=1+x+2!x^2+3!x^3+\ldots \nonumber \]

обидва силові ряди зосереджені$x=0.$ на серії

\[\sum_{n=0}^∞\dfrac{(x−2)^n}{(n+1)3^n}=1+\dfrac{x−2}{2⋅3}+\dfrac{(x−2)^2}{3⋅3^2}+\dfrac{(x−2)^3}{4⋅3^3}+\ldots \nonumber \]

це силовий ряд, зосереджений на$x=2$.

Конвергенція силового ряду

Оскільки терміни в ряді степенів включають змінну$x$, ряд може сходитися для певних значень$x$ і розходитися для інших значень$x$. Для степеневого ряду$x=a$, зосередженого на, значення ряду at$x=a$ задається за допомогою$c_0$. Тому силовий ряд завжди сходиться в його центрі. Деякі силові ряди сходяться тільки при такому значенні$x$. Більшість силових рядів, однак, сходяться для більш ніж одного значення$x$. У цьому випадку степеневий ряд або сходиться для всіх дійсних чисел,$x$ або сходиться для всіх$x$ у скінченному інтервалі. Наприклад, геометричний ряд$\displaystyle \sum_{n=0}^∞x^n$ сходиться для всіх$x$ в інтервалі$(−1,1)$, але розходиться для всіх$x$ поза цим інтервалом. Зараз ми підсумовуємо ці три можливості для загального енергетичного ряду.

Примітка$\PageIndex{1}$: Convergence of a Power Series

Розглянемо силовий ряд$\displaystyle \sum_{n=0}^∞c_n(x−a)^n.$ ряд задовольняє саме одному з наступних властивостей:

Серія сходиться на$x=a$ і розходиться для всіх$x≠a.$
Ряд сходиться для всіх дійсних чисел$x$.
Існує дійсне число$R>0$ таке, що ряд сходиться якщо$|x−a|<R$ і розходиться якщо$|x−a|>R$. При значеннях$x$, де |x−a|=R, ряд може сходитися або розходитися.

Доказ

Припустимо, що силовий ряд зосереджений на$a=0$. (Для серії, зосередженої на значенні, відмінному від нуля, результат випливає, дозволяючи$y=x−a$ та враховуючи ряд

\[ \sum_{n=1}^∞c_ny^n. \nonumber \]

Треба спочатку довести наступний факт:

Якщо існує дійсне число$d≠0$ таке, що$\displaystyle \sum_{n=0}^∞c_nd^n$ сходиться, то ряд$\displaystyle \sum_{n=0}^∞c_nx^n$ сходиться абсолютно для всіх$x$ таких, що$|x|<|d|.$

Оскільки$\displaystyle \sum_{n=0}^∞c_nd^n$ сходиться, то$c_nd^n→0$ n-ий термін був$n→∞$. Тому існує ціле число$N$ таке, що$|c_nd^n|≤1$ для всіх$n≥N.$ Writing

\[|c_nx^n|=|c_nd^n| \left|\dfrac{x}{d}\right|^n, \nonumber \]

робимо висновок, що для всіх N≥n

\[|c_nx^n|≤\left|\dfrac{x}{d}\right|^n. \nonumber \]

Серіал

\[\sum_{n=N}^∞\left|\dfrac{x}{d}\right|^n \nonumber \]

це геометричний ряд, який сходиться, якщо$|\dfrac{x}{d}|<1.$ Тому, шляхом тесту порівняння, ми робимо висновок, що$\displaystyle \sum_{n=N}^∞c_nx^n$ також сходиться для$|x|<|d|$. Оскільки ми можемо додати скінченну кількість членів до збіжному ряду, ми робимо висновок, що$\displaystyle \sum_{n=0}^∞c_nx^n$ сходиться для$|x|<|d|.$

За допомогою цього результату ми тепер можемо довести теорему. Розглянемо серію

\[\sum_{n=0}^∞a_nx^n \nonumber \]

і нехай$S$ буде набір дійсних чисел, для яких серія сходиться. Припустимо, що набір$S={0}.$ Тоді серія потрапляє під випадок i.

Припустимо, що$S$ множина - це сукупність всіх дійсних чисел. Потім ряд потрапляє під випадок ii. Припустимо, що$S≠{0}$ і не$S$ є безліччю дійсних чисел. Тоді існує дійсне число$x*≠0$ таке, що ряд не сходиться. Таким чином, серія не може сходитися ні для одного$x$ такого, що$|x|>|x*|$. Тому множина$S$ повинна бути обмеженою множиною, а значить, вона повинна мати найменшу верхню межу. (Цей факт випливає з найменш верхньої межі властивості для дійсних чисел, який виходить за рамки цього тексту і висвітлюється в реальних курсах аналізу.) Назвіть цю найменшу верхню межу$R$. З тих пір$S≠{0}$, число$R>0$. Тому ряд сходиться для всіх$x$ таких, що$|x|<R,$ і ряд потрапляє в case iii.

□

Якщо ряд$\displaystyle \sum_{n=0}^∞c_n(x−a)^n$ потрапляє в випадок iii. Note, то ряд сходиться для всіх$x$ таких, що$|x−a|<R$ для деяких$R>0$, і розходиться для всіх$x$ таких що$|x−a|>R$. Ряд може сходитися або розходитися при значеннях$x$ де$|x−a|=R$. Набір значень,$x$ для яких$\displaystyle \sum_{n=0}^∞c_n(x−a)^n$ сходиться ряд, відомий як інтервал збіжності. Так як ряд розходиться для всіх значень$x$ де$|x−a|>R$, довжина інтервалу дорівнює$2R$, а значить, радіус інтервалу дорівнює$R$. Значення$R$ називається радіусом збіжності. Наприклад, оскільки ряд$\displaystyle \sum_{n=0}^∞x^n$ сходиться для всіх значень$x$ в інтервалі$(−1,1)$ і розходиться для всіх значень$x$ таким чином$|x|≥1$, інтервал збіжності цього ряду дорівнює$(−1,1)$. Так як довжина інтервалу дорівнює$2$, радіус збіжності дорівнює$1$.

Визначення: радіус збіжності

Розглянемо силові ряди$\displaystyle \sum_{n=0}^∞c_n(x−a)^n$. Безліч дійсних чисел$x$, де сходиться ряд, є інтервалом збіжності. Якщо існує дійсне число,$R>0$ таке, що ряд сходиться для$|x−a|<R$ і розходиться для$|x−a|>R,$ тоді$R$ радіус збіжності. Якщо ряд сходиться тільки на$x=a$, ми говоримо радіус збіжності є$R=0$. Якщо ряд сходиться для всіх дійсних чисел$x$, ми говоримо, що радіус збіжності дорівнює$R=∞$ (рис.$\PageIndex{1}$).

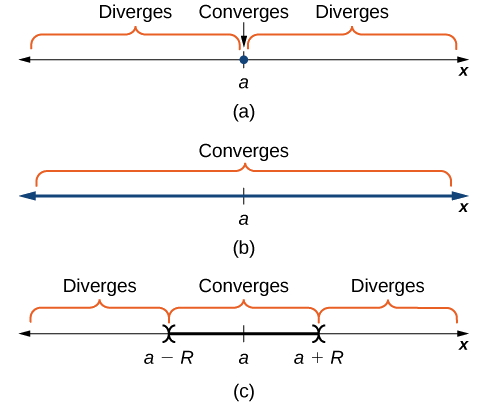
Ця цифра має три числові лінії, кожна з яких позначена x. Посередині кожної цифрової лінії знаходиться точка з позначкою a. Перша цифра має «розходиться» по всій лінії ліворуч від a і «розходиться» над лінією праворуч від a. У самій точці a вона позначена як «сходиться». Другий числовий рядок має «сходиться», позначені для всього рядка. Третя цифра має точки з позначками A-r, a та A+r. Ліворуч від A-r числовий рядок позначено «розходиться». Між A-r і A+r числовий рядок позначений «сходиться», а праворуч від A+r числовий рядок позначено «розходиться». — Рисунок$\PageIndex{1}$: Для послідовного$\displaystyle \sum_{n=0}^∞c_n(x−a)^n$ графіка (а) показує радіус збіжності в$R=0$, графік (b) показує радіус збіжності в$R=∞$, а графік (c) показує радіус збіжності в$R$. Для графа (c) зауважимо, що ряди можуть сходитися або не сходитися в кінцевих точках$x=a+R$ і$x=a−R$.

Щоб визначити інтервал збіжності для степеневого ряду, ми зазвичай застосовуємо тест коефіцієнта. У прикладі$\PageIndex{1}$ ми показуємо три різні можливості, проілюстровані на малюнку$\PageIndex{1}$.

Приклад$\PageIndex{1}$: Finding the Interval and Radius of Convergence

Для кожного з наступних рядів знайдіть інтервал і радіус збіжності.

$\displaystyle \sum_{n=0}^∞\dfrac{x^n}{n!}$
$\displaystyle \sum_{n=0}^∞n!x^n$
$\displaystyle \sum_{n=0}^∞\dfrac{(x−2)^n}{(n+1)3^n}$

Рішення

а. щоб перевірити на збіжність, застосуйте тест коефіцієнта. У нас є

\ [\ почати {вирівнювати*} ρ &=\ lim_ {n→∞}\ ліворуч |\ dfrac {\ dfrac {x^ {n+1}} {(n+1)!}} {\ dfrac {x^n} {n!}} \ праворуч |\\ [4pt]
&=\ lim_ {n → ∞}\ ліворуч |\ dfrac {x^ {n+1}} {(n+1)!} ⋅\ фрак {n!} {x^n}\ праворуч |\\ [4pt]
&=\ lim_ {n → ∞}\ ліворуч |\ dfrac {x^ {n+1}} {(n+1) ⋅n!} ⋅\ фрак {n!} {x^n}\ праворуч |\\ [4pt]
&=\ lim_ {n → ∞}\ ліворуч |\ dfrac {x} {n+1}\ праворуч |\\ [4pt]
&=|x|\ lim_ {n →∞}\ dfrac {1} {n+1}\\ [4pt]
&=0<1\ кінець {вирівня*}\]

для всіх значень$x$. Тому ряд сходиться для всіх дійсних чисел$x$. Інтервал збіжності дорівнює,$(−∞,∞)$ а радіус збіжності дорівнює$R=∞.$

б Нанесіть тест на співвідношення. Бо$x≠0$, ми бачимо, що

\ [\ почати {вирівнювати*} ρ &=\ lim_ {n→∞}\ ліворуч |\ dfrac {(n+1)! x^ {n+1}} {n! x^n}\ праворуч |\\ [4пт]
&=\ lim_ {n→∞} | (n+1) x |\\ [4pt]
&=|x|\ lim_ {n→∞} (n+1)\\ [4pt]
&=∞. \ end {вирівнювати*}\]

Тому серія розходиться у всіх$x≠0$. Так як ряд по центру$x=0$, він повинен сходитися там, тому ряд сходиться тільки для$x≠0$. Інтервал збіжності - одиничне значення,$x=0$ а радіус збіжності -$R=0$.

c Для того, щоб застосувати тест співвідношення, розглянемо

\ [\ почати {вирівнювати*} ρ &=\ lim_ {n→∞}\ ліво|\ dfrac {\ dfrac {(x−2) ^ {n+1}} {(n+2) 3^ {n+1}} {\ dfrac {(x−2) ^n} {(n+1) 3^n}}\ право|\\ [4пт]
&=\ lim _ {n→∞}\ ліворуч |\ dfrac {(x−2) ^ {n+1}} {(n+2) 3^ {n+1}} ⋅\ dfrac {(n+1) 3^n} {(x−2) ^n}\ праворуч |\\ [4pt]
&=\ lim_ {n→∞}\ ліво|\ dfrac {(x−2) (n+1)} {3 (n+2)}\ праворуч |\\ [4 pt]
&=\ dfrac {|x−2|} {3}. \ end {вирівнювати*}\]

Співвідношення$ρ<1$ if$|x−2|<3$. Так як$|x−2|<3$ має$−3<x−2<3,$ на увазі, що ряд сходиться абсолютно якщо$−1<x<5$. Співвідношення$ρ>1$ if$|x−2|>3$. Тому ряд розходиться, якщо$x<−1$ або$x>5$. Тест на співвідношення є непереконливим, якщо$ρ=1$. Співвідношення$ρ=1$ якщо і тільки якщо$x=−1$ або$x=5$. Нам потрібно перевірити ці значення$x$ окремо. Для$x=−1$, серія дається

\[ \sum_{n=0}^∞\dfrac{(−1)^n}{n+1}=1−\dfrac{1}{2}+\dfrac{1}{3}−\dfrac{1}{4}+\ldots . \nonumber \]

Так як це змінний гармонійний ряд, то він сходиться. Таким чином, ряд сходиться при$x=−1$. Для$x=5$, серія дається

\[ \sum_{n=0}^∞\dfrac{1}{n+1}=1+\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+\ldots . \nonumber \]

Це гармонійний ряд, який розходиться. Тому силовий ряд розходиться на$x=5$. Зроблено висновок, що інтервал збіжності дорівнює$[−1,5)$ і радіус збіжності дорівнює$R=3$.

Вправа$\PageIndex{1}$

Знайти інтервал і радіус збіжності для ряду

\[ \sum_{n=1}^∞\dfrac{x^n}{\sqrt{n}}. \nonumber \]

Підказка: Застосуйте тест співвідношення, щоб перевірити абсолютну збіжність.

Відповідь: Інтервал збіжності -$[−1,1).$ Радіус збіжності дорівнює$R=1.$

Представлення функцій як енергетичних рядів

Можливість представляти функцію за допомогою «нескінченного многочлена» є потужним інструментом. Поліноміальні функції - це найпростіші функції для аналізу, оскільки вони включають лише основні арифметичні операції додавання, віднімання, множення та ділення. Якщо ми можемо представити складну функцію нескінченним многочленом, ми можемо використовувати поліноміальне подання для її диференціації або інтеграції. Крім того, ми можемо використовувати усічений варіант поліноміального виразу для наближення значень функції. Отже, питання в тому, коли ми можемо представляти функцію силовим рядом?

Розглянемо ще раз геометричні ряди

\[1+x+x^2+x^3+\ldots =\sum_{n=0}^∞x^n. \nonumber \]

Нагадаємо, що геометричний ряд

\[a+ar+ar^2+ar^3+\ldots \nonumber \]

сходиться, якщо і тільки якщо$|r|<1.$ У цьому випадку він сходиться до$\dfrac{a}{1−r}$. Тому якщо$|x|<1$, ряд в прикладі$\PageIndex{1}$ сходиться до$\dfrac{1}{1−x}$ і пишемо

\[1+x+x^2+x^3+\ldots =\dfrac{1}{1−x} for|x|<1. \nonumber \]

В результаті ми можемо представляти функцію$f(x)=\dfrac{1}{1−x}$ силовим рядом

\[1+x+x^2+x^3+\ldots when|x|<1. \nonumber \]

Тепер ми покажемо графічно, як цей ряд забезпечує уявлення для функції,$f(x)=\dfrac{1}{1−x}$ порівнюючи графік$f$ з графіками декількох часткових сум цього нескінченного ряду.

Приклад$\PageIndex{2}$: Graphing a Function and Partial Sums of its Power Series

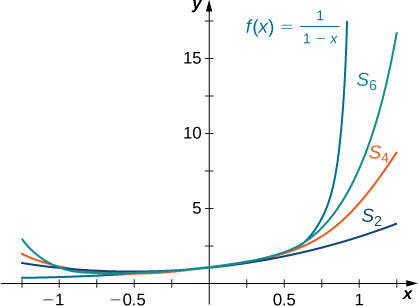
Намалюйте графік$f(x)=\dfrac{1}{1−x}$ і графіки відповідних часткових сум$ \displaystyle S_N(x)=\sum_{n=0}^Nx^n$ для$N=2,4,6$ інтервалу$(−1,1)$. Коментуйте наближення$S_N$ у міру$N$ збільшення.

Рішення

З графіка на малюнку ви бачите, що зі$N$ збільшенням$S_N$ стає кращим наближенням для$f(x)=\dfrac{1}{1−x}$ для$x$ в інтервалі$(−1,1)$.

Ця цифра є графіком y = 1/ (1-x), який є зростаючою кривою з вертикальною асимптотою на 1. Також на цьому графіку наведено три часткові суми функції, S sub 6, S sub 4 та S sub 2. Ці криві, по порядку, поступово стають більш плоскі. — Рисунок$\PageIndex{2}$: Графік показує функцію та три її наближення частковими сумами степеневого ряду.

Вправа$\PageIndex{2}$

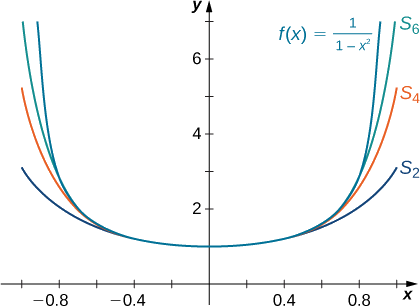
Намалюйте графік$f(x)=\dfrac{1}{1−x^2}$ та відповідні часткові суми$\displaystyle S_N(x)=\sum_{n=0}^Nx^{2n}$ для$N=2,4,6$ на інтервалі$(−1,1).$

Підказка: $S_N(x)=1+x^2+\ldots +x^{2N}=\dfrac{1−x^{2(N+1)}}{1−x^2}$

Відповідь: $Ця цифра є графіком y = 1/ (1-x^2), який являє собою криву, увігнуту вгору, симетричну щодо осі y. Також на цьому графіку наведено три часткові суми функції, S sub 6, S sub 4 та S sub 2. Ці криві, по порядку, поступово стають більш плоскі.$

Далі ми розглянемо функції, що містять вираз, подібний до суми геометричного ряду, і показуємо, як представляти ці функції за допомогою степеневих рядів.

Приклад$\PageIndex{3}$: Representing a Function with a Power Series

Використовуйте силовий ряд, щоб представити кожну з наступних функцій$f$. Знайти інтервал збіжності.

$f(x)=\dfrac{1}{1+x^3}$
$f(x)=\dfrac{x^2}{4−x^2}$

Рішення

a Ви повинні розпізнати цю функцію$f$ як суму геометричного ряду, тому що

\[ \dfrac{1}{1+x^3}=\dfrac{1}{1−(−x^3)}. \nonumber \]

Використовуючи той факт, що, for$|r|<1,\dfrac{a}{1−r}$ - сума геометричного ряду

\[ \sum_{n=0}^∞ar^n=a+ar+ar^2+\ldots , \nonumber \]

ми бачимо, що для$|−x^3|<1,$

\[ \begin{align*} \dfrac{1}{1+x^3} =\dfrac{1}{1−(−x^3)} \\[4pt] =\sum_{n=0}^∞(−x^3)^n \\[4pt] =1−x^3+x^6−x^9+\ldots . \end{align*}\]

Оскільки цей ряд сходиться якщо і тільки якщо$|−x^3|<1$, інтервал збіжності є$(−1,1)$, і ми маємо

\[ \dfrac{1}{1+x^3}=1−x^3+x^6−x^9+\ldots for|x|<1.\nonumber \]

б Ця функція не є точною формою суми геометричного ряду. Однак за допомогою невеликої алгебраїчної маніпуляції ми можемо віднести f до геометричного ряду. Факторингом 4 з двох членів в знаменнику отримаємо

\[ \begin{align*} \dfrac{x^2}{4−x^2} =\dfrac{x^2}{4(\dfrac{1−x^2}{4})}\\[4pt] =\dfrac{x^2}{4(1−(\dfrac{x}{2})^2)}.\end{align*}\]

Тому ми маємо

\ [\ почати {вирівнювати*}\ dfrac {x^2} {4−x^2} &=\ dfrac {x^2} {4 (1 − (\ dfrac {x} {2}) ^2) ^2)}\\ [4pt]
&=\ dfrac {\ dfrac {x^2} {4}} {1− (\ dfrac {x} {2}) ^2}\\ [4pt]
&=\ сума_ {n=0} ^∞\ dfrac {x^2} {4} (\ dfrac {x} {2}) ^ {2n}. \ end {вирівнювати*}\]

Ряд сходиться до тих пір, поки$|(\dfrac{x}{2})^2|<1$ (зверніть увагу, що коли$|(\dfrac{x}{2})^2|=1$ ряд не сходиться). Вирішуючи цю нерівність, робимо висновок, що інтервал збіжності дорівнює$(−2,2)$ і

\ [\ почати {вирівнювати*}\ dfrac {x^2} {4−x^2} &=\ сума {n=0} ^∞\ dfrac {x^ {2n+2}} {4^ {n+1}}\ [4pt]
&=\ dfrac {x^2} {4} +\ dfrac {x^4} {4^2} +\ dfrac {x^6} {4^3} +\ ldots\ кінець {align*}\]

для$|x|<2.$

Вправа$\PageIndex{3}$

Уявіть функцію$f(x)=\dfrac{x^3}{2−x}$ за допомогою степеневого ряду і знайдіть інтервал збіжності.

Підказка: Перепишіть f в форму$f(x)=\dfrac{g(x)}{1−h(x)}$ для деяких функцій$g$ і$h$.

Відповідь: $\displaystyle \sum_{n=0}^∞\dfrac{x^{n+3}}{2^{n+1}}$з інтервалом сходження$(−2,2)$

В інших розділах цієї глави ми покажемо способи отримання уявлень рядів потужності для багатьох інших функцій, а також як ми можемо використовувати ці уявлення для оцінки, диференціації та інтеграції різних функцій.

Ключові поняття

Для силового ряду, зосередженого на$x=a$, утримується одна з наступних трьох властивостей:
- i. силовий ряд сходиться тільки при$x=a$. В даному випадку скажемо, що радіус збіжності є$R=0$.
- II. Силовий ряд сходиться для всіх дійсних чисел$x$. В даному випадку скажемо, що радіус збіжності є$R=∞$.
- III. Існує дійсне число R таке, що ряд сходиться для$|x−a|<R$ і розходиться для$|x−a|>R$. При цьому радіус збіжності дорівнює$R.$
Якщо силовий ряд сходиться на скінченному інтервалі, ряд може сходитися або не сходитися в кінцевих точках.
Тест коефіцієнта часто може бути використаний для визначення радіуса збіжності.
Геометричний ряд$\displaystyle \sum_{n=0}^∞x^n=\dfrac{1}{1−x}$ для$|x|<1$ дозволяє нам представляти певні функції за допомогою геометричних рядів.

Ключові рівняння

Потужність серії в центрі$x=0$

\[ \sum_{n=0}^∞c_nx^n=c_0+c_1x+c_2x^2+\ldots n\nonumber \]

Потужність серії в центрі$x=a$

\[ \sum_{n=0}^∞c_n(x−a)^n=c_0+c_1(x−a)+c_2(x−a)^2+\ldots \nonumber \]

Глосарій

інтервал зближення: множина дійсних чисел,$x$ для яких зближується степеневий ряд

силовий ряд: серія форми$\displaystyle \sum_{n=0}^∞c_nx^n$ - це силовий ряд з центром$x=0$; серія форми$\displaystyle \sum_{n=0}^∞c_n(x−a)^n$ є силовий ряд, зосереджений на$x=a$

радіус збіжності: якщо існує дійсне число$R>0$ таке, що енергетичний ряд з центром$x=a$ сходиться для$|x−a|<R$ і розходиться для$|x−a|>R$, то$R$ є радіусом збіжності; якщо ряди потужності сходяться тільки в$x=a$, радіус збіжності є$R=0$; якщо потужність ряд сходиться для всіх дійсних чисел$x$, радіус збіжності дорівнює$R=∞$

Визначення\(\PageIndex{1}\): Power Series

Примітка\(\PageIndex{1}\): Convergence of a Power Series

Доказ

Визначення: радіус збіжності

Приклад\(\PageIndex{1}\): Finding the Interval and Radius of Convergence

Вправа\(\PageIndex{1}\)

Приклад\(\PageIndex{2}\): Graphing a Function and Partial Sums of its Power Series

Вправа\(\PageIndex{2}\)

Приклад\(\PageIndex{3}\): Representing a Function with a Power Series

Вправа\(\PageIndex{3}\)