4.2: Лінійні наближення та диференціали

Цілі навчання

• Опишіть лінійне наближення до функції в точці.
• Запишіть лінеаризацію заданої функції.
• Намалюйте графік, який ілюструє використання диференціалів для наближення зміни кількості.
• Обчисліть відносну похибку і процентну похибку за допомогою диференціального наближення.

Ми щойно бачили, як похідні дозволяють нам порівнювати пов'язані величини, які змінюються з часом. У цьому розділі ми розглянемо ще одне застосування похідних: можливість наближення функцій локально лінійними функціями. Лінійні функції є найпростішими функціями, з якими працювати, тому вони забезпечують корисний інструмент для наближення значень функцій. Крім того, ідеї, представлені в цьому розділі, узагальнюються пізніше в тексті, коли ми вивчаємо, як наблизити функції поліномами вищого ступеня Вступ до степенних рядів і функцій.

Лінійне наближення функції в точці

Розглянемо функцію$f$, яка диференціюється в точці$x=a$. Нагадаємо, що дотична пряма до графіка$f$ at$a$ задається рівнянням

$$y=f(a)+f'(a)(x−a). \nonumber$$

Наприклад, розглянемо функцію за$f(x)=\frac{1}{x}$ адресою$a=2$. Оскільки$f$ диференціюється при$x=2$ і$f'(x)=−\frac{1}{x^2}$, ми бачимо, що$f'(2)=−\frac{1}{4}$. Тому дотична пряма до графіка$f$ at$a=2$ задається рівнянням

$$y=\frac{1}{2}−\frac{1}{4}(x−2). \nonumber$$

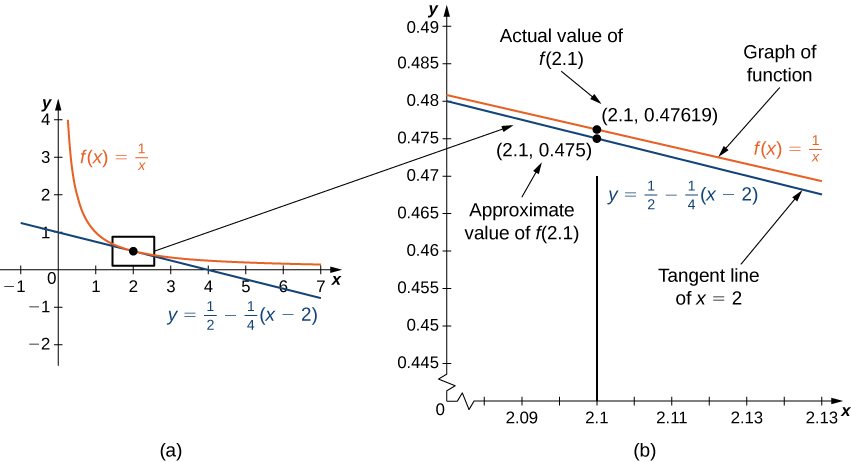
На малюнку$\PageIndex{1a}$ показаний графік$f(x)=\frac{1}{x}$ разом з дотичною лінією до$f$ at$x=2$. Зауважте$2$, що для$x$ ближнього, графік дотичної прямої близький до графіка$f$. В результаті ми можемо використовувати рівняння дотичної прямої$f(x)$ для$x$ наближення$2$. Наприклад, якщо$x=2.1$,$y$ значення відповідної точки на дотичній прямій дорівнює

$$y=\frac{1}{2}−\frac{1}{4}(2.1−2)=0.475. \nonumber$$

Фактичне значення$f(2.1)$ задається

$$f(2.1)=\frac{1}{2.1}≈0.47619. \nonumber$$

Тому дотична лінія дає нам досить хороше наближення$f(2.1)$ (рис.$\PageIndex{1b}$). Однак зауважте, що для значень$x$$2$ далеких від рівняння дотичної прямої не дає нам хорошого наближення. Наприклад, if$x=10$,$y$ -значення відповідної точки на дотичній прямій дорівнює

$$y=\frac{1}{2}−\frac{1}{4}(10−2)=\frac{1}{2}−2=−1.5, \nonumber$$

тоді як значення функції at$x=10$ дорівнює$f(10)=0.1.$

Рисунок$\PageIndex{1}$: (a) Дотична лінія до$f(x)=1/x$ at$x=2$ забезпечує хороше наближення до$f$ for$x$ near$2$. (б) В$x=2.1$, значення$y$ на дотичній лінії до$f(x)=1/x$ є$0.475$. Фактичне значення$f(2.1)$ є$1/2.1$, яке приблизно$0.47619$.

Загалом, для диференційовної функції$f$ рівняння дотичної прямої до$f$ at$x=a$ може бути використано$f(x)$ для$x$ наближення$a$. Тому ми можемо написати

$f(x)≈f(a)+f'(a)(x−a)$для$x$ ближнього$a$.

Викликаємо лінійну функцію

$$L(x)=f(a)+f'(a)(x−a) \label{linearapprox}$$

лінійне наближення, або дотичне наближення прямої,$f$ at$x=a$. Ця функція також$L$ відома як лінеаризація$f$ at$x=a.$

Щоб показати, наскільки корисним може бути лінійне наближення, ми розглянемо, як знайти лінійне наближення для$f(x)=\sqrt{x}$ at$x=9.$

Приклад$\PageIndex{1}$: Linear Approximation of $\sqrt{x}$

Знайдіть лінійне наближення$f(x)=\sqrt{x}$ at$x=9$ і використовуйте наближення для оцінки$\sqrt{9.1}$.

Рішення

Оскільки ми шукаємо лінійне наближення при$x=9,$ використанні Equation\ ref {linearapx}, ми знаємо, що лінійне наближення задається

$$L(x)=f(9)+f'(9)(x−9). \nonumber$$

Нам потрібно знайти$f(9)$ і$f'(9).$

$f(x)=\sqrt{x}⇒f(9)=\sqrt{9}=3$

$f'(x)=\frac{1}{2\sqrt{x}}⇒f'(9)=\frac{1}{2\sqrt{9}}=\frac{1}{6}$

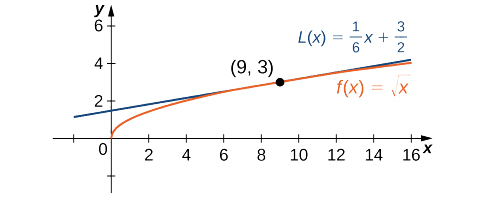
Тому лінійне наближення задається малюнком$\PageIndex{2}$.

$$L(x)=3+\frac{1}{6}(x−9) \nonumber$$

Використовуючи лінійне наближення, ми можемо оцінити,$\sqrt{9.1}$ написавши

$$\sqrt{9.1}=f(9.1)≈L(9.1)=3+\frac{1}{6}(9.1−9)≈3.0167. \nonumber$$

Рисунок$\PageIndex{2}$: Локальне лінійне наближення до$f(x)=\sqrt{x}$ at$x=9$ забезпечує наближення до$f$ for$x$ near$9$.

Аналіз

За допомогою калькулятора значення$\sqrt{9.1}$ до чотирьох знаків після коми дорівнює$3.0166$. Значення, задане лінійним наближенням$3.0167$, дуже близьке до значення, отриманого за допомогою калькулятора, тому виявляється, що використання цього лінійного наближення є хорошим способом оцінки$\sqrt{x}$, принаймні для x поблизу$9$. У той же час, може здатися дивним використовувати лінійне наближення, коли ми можемо просто натиснути кілька кнопок на калькуляторі для оцінки$\sqrt{9.1}$. Однак як оцінює калькулятор$\sqrt{9.1}$? Калькулятор використовує наближення! Насправді калькулятори та комп'ютери весь час використовують наближення для оцінки математичних виразів; вони просто використовують наближення більш високого ступеня.

Вправа$\PageIndex{1}$

Знайти локальне лінійне наближення до$f(x)=\sqrt[3]{x}$ at$x=8$. Використовуйте його для наближення$\sqrt[3]{8.1}$ до п'яти знаків після коми.

Підказка

$L(x)=f(a)+f'(a)(x−a)$

Відповідь

$L(x)=2+\frac{1}{12}(x−8);$$2.00833$

Приклад$\PageIndex{2}$: Linear Approximation of $\sin x$

Знайдіть лінійне наближення$f(x)=\sin x$ at$x=\frac{π}{3}$ і використовуйте його для наближення$\sin(62°).$

Рішення

Спочатку зауважимо, що оскільки$\frac{π}{3}$ rad еквівалентний$60°$, використання лінійного наближення при$x=π/3$ здається розумним. Лінійне наближення задається

$L(x)=f(\frac{π}{3})+f'(\frac{π}{3})(x−\frac{π}{3}).$

Ми бачимо, що

$f(x)=\sin x ⇒f(\frac{π}{3})=\sin(\frac{π}{3})=\frac{\sqrt{3}}{2}$

$f'(x)=\cos x ⇒f'(\frac{π}{3})=\cos(\frac{π}{3})=\frac{1}{2}$

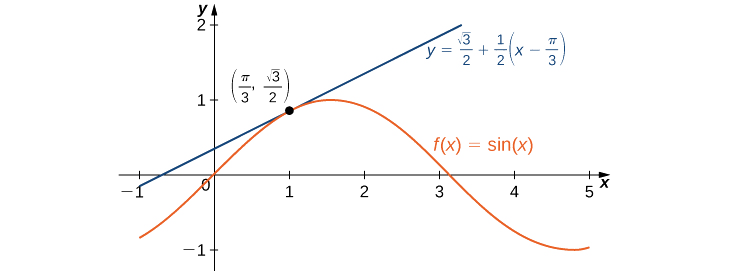
Тому лінійне наближення$f$ at$x=π/3$ задається малюнком$\PageIndex{3}$.

$L(x)=\frac{\sqrt{3}}{2}+\frac{1}{2}(x−\frac{π}{3})$

Щоб оцінити$\sin(62°)$ використання$L$, ми повинні спочатку$62°$ перетворити на радіани. У нас є$62°=\frac{62π}{180}$ радіани, тому оцінка для$\sin(62°)$ дається

$\sin(62°)=f(\frac{62π}{180})≈L(\frac{62π}{180})=\frac{\sqrt{3}}{2}+\frac{1}{2}(\frac{62π}{180}−\frac{π}{3})=\frac{\sqrt{3}}{2}+\frac{1}{2}(\frac{2π}{180})=\frac{\sqrt{3}}{2}+\frac{π}{180}≈0.88348.$

Рисунок$\PageIndex{3}$: Лінійне наближення до$f(x)=\sin x$ at$x=π/3$ забезпечує наближення до$\sin x$ for$x$ near$π/3.$

Вправа$\PageIndex{2}$

Знайти лінійне наближення для$f(x)=\cos x$ at$x=\frac{π}{2}.$

Підказка

$L(x)=f(a)+f'(a)(x−a)$

Відповідь

$L(x)=−x+\frac{π}{2}$

Лінійні наближення можуть бути використані при оцінці коренів і повноважень. У наступному прикладі ми знаходимо лінійне наближення для$f(x)=(1+x)^n$ at$x=0$, яке може бути використано для оцінки коренів і степеней для дійсних чисел поблизу$1$. Та ж ідея може бути поширена на функцію форми$f(x)=(m+x)^n$ для оцінки коренів і повноважень поблизу іншого числа$m$.

Приклад$\PageIndex{3}$: Approximating Roots and Powers

Знайти лінійне наближення$f(x)=(1+x)^n$ at$x=0$. Використовуйте це наближення для оцінки$(1.01)^3.$

Рішення

Лінійне наближення при$x=0$ задається

$L(x)=f(0)+f'(0)(x−0).$

Тому що

$f(x)=(1+x)^n⇒f(0)=1$

$f'(x)=n(1+x)^{n−1}⇒f'(0)=n,$

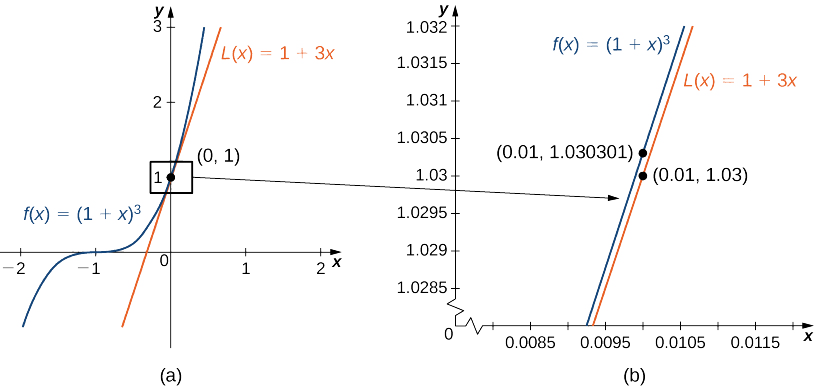
лінійне наближення задається малюнком$\PageIndex{4a}$.

$L(x)=1+n(x−0)=1+nx$

Ми можемо наблизити$(1.01)^3$, оцінивши$L(0.01)$, коли$n=3$. Ми робимо висновок, що

$(1.01)^3=f(1.01)≈L(1.01)=1+3(0.01)=1.03.$

Малюнок$\PageIndex{4}$: (а) Лінійне наближення$f(x)$ at$x=0$ є$L(x)$. (б) Фактичне значення$1.01^3$ є$1.030301$. Лінійне наближення$f(x)$ at$x=0$$1.01^3$ оцінок бути$1.03$.

Вправа$\PageIndex{3}$

Знайдіть лінійне наближення$f(x)=(1+x)^4$ at$x=0$ без використання результату з попереднього прикладу.

Підказка

$f'(x)=4(1+x)^3$

Відповідь

$L(x)=1+4x$

Диференціали

Ми бачили, що лінійні наближення можуть бути використані для оцінки значень функцій. Вони також можуть бути використані для оцінки суми зміни значення функції в результаті невеликої зміни вхідних даних. Щоб обговорити це більш формально, ми визначимо пов'язане поняття: диференціали. Диференціали надають нам спосіб оцінки суми, яку функція змінює внаслідок невеликої зміни вхідних значень.

Коли ми вперше розглянули похідні, ми використовували позначення Лейбніца$dy/dx$ для представлення$y$ похідної щодо$x$. Хоча ми використовували вирази$dy$ і$dx$ в цьому позначенні, вони не мали сенсу самостійно. Тут ми бачимо сенс до виразів$dy$ і$dx$. Припустимо$y=f(x)$, це диференційована функція. $dx$Дозволяти бути незалежною змінною, якій може бути присвоєно будь-яке ненульове дійсне число, і визначити залежну змінну$dy$

$$dy=f'(x)\,dx. \label{diffeq}$$

Важливо зауважити, що$dy$ є функцією обох$x$ і$dx$. Вирази$dy$ і$dx$ називаються диференціалами. Ми можемо розділити обидві сторони рівняння\ ref {diffeq}$dx,$, на яке дає

$$\frac{dy}{dx}=f'(x). \label{inteq}$$

Це звичне нам вираз для позначення похідної. Рівняння\ ref {inteq} відоме як диференціальна форма рівняння\ ref {diffeq}.

Приклад$\PageIndex{4}$: Computing Differentials

Для кожної з наступних функцій знайдіть$dy$ і оцініть, коли$x=3$ і$dx=0.1.$

1. $y=x^2+2x$
2. $y=\cos x$

Рішення

Ключовим кроком є обчислення похідної. Коли ми маємо це, ми можемо отримати$dy$ безпосередньо.

а Оскільки$f(x)=x^2+2x,$ ми знаємо$f'(x)=2x+2$, і тому

$dy=(2x+2)\,dx.$

Коли$x=3$ і$dx=0.1,$

$dy=(2⋅3+2)(0.1)=0.8.$

б. так як$f(x)=\cos x , f'(x)=−\sin(x).$ це дає нам

$dy=−\sin x \,dx.$

Коли$x=3$ і$dx=0.1,$

$dy=−\sin(3)(0.1)=−0.1\sin(3).$

Вправа$\PageIndex{4}$

Для$y=e^{x^2}$, знайдіть$dy$.

Підказка

$dy=f'(x)\,dx$

Відповідь

$dy=2xe^{x^2}dx$

Тепер ми підключаємо диференціали до лінійних наближень. Диференціали можуть бути використані для оцінки зміни значення функції в результаті невеликої зміни вхідних значень. Розглянемо функцію$f$, яка диференційована в точці$a$. Припустимо, що вхід$x$ змінюється на невелику суму. Нас цікавить, наскільки$y$ змінюється вихід. Якщо$x$ змінюється від$a$ до$a+dx$, то зміна в$x$ є$dx$ (також позначається$Δx$), а зміна в$y$ задається

$$Δy=f(a+dx)−f(a). \nonumber$$

Однак замість того$y$, щоб обчислювати точну зміну, часто простіше наблизити зміну за$y$ допомогою лінійного наближення. Для$x$ ближнього$a, f(x)$ можна наблизити лінійним наближенням (Equation\ ref {linearaprox})

$$L(x)=f(a)+f'(a)(x−a). \nonumber$$

Тому якщо$dx$ мало,

$$f(a+dx)≈L(a+dx)=f(a)+f'(a)(a+dx−a). \nonumber$$

Тобто,

$$f(a+dx)−f(a)≈L(a+dx)−f(a)=f'(a)\,dx. \nonumber$$

Іншими словами, фактична зміна функції$f$ якщо$x$ збільшується від$a$ до приблизно$a+dx$ дорівнює різниці між$L(a+dx)$ і$f(a)$, де$L(x)$ - лінійне наближення$f$ at$a$. За визначенням$L(x)$, ця різниця дорівнює$f'(a)\,dx$. Підсумовуючи,

$$Δy=f(a+dx)−f(a)≈L(a+dx)−f(a)=f'(a)\,dx=dy. \nonumber$$

Тому ми можемо використовувати диференціал$dy=f'(a)\,dx$ для наближення зміни,$y$ якщо$x$ збільшується від$x=a$ до$x=a+dx$. Ми можемо побачити це на наступному графіку.

Малюнок$\PageIndex{5}$: Диференціал$dy=f'(a)\,dx$ використовується для наближення фактичної зміни,$y$ якщо$x$ збільшується від$a$ до$a+dx$.

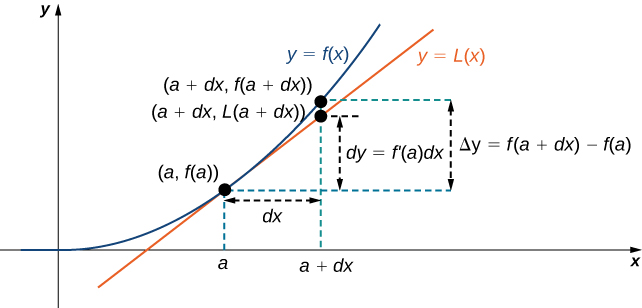
Тепер ми розглянемо, як використовувати диференціали для наближення зміни значення функції, що виникає в результаті невеликої зміни значення вхідних даних. Зверніть увагу, що розрахунок з диференціалами набагато простіше, ніж обчислення фактичних значень функцій, і результат дуже близький до того, що ми отримали б при більш точному обчисленні.

Приклад$\PageIndex{5}$: Approximating Change with Differentials

Дозвольте$y=x^2+2x.$$Δy$ обчислювати і$dy$ при$x=3$ якщо$dx=0.1.$

Рішення

Фактична зміна,$y$ якщо$x$ змінюється від$x=3$ до$x=3.1$, задається

$Δy=f(3.1)−f(3)=[(3.1)^2+2(3.1)]−[3^2+2(3)]=0.81.$

Орієнтовна зміна в$y$ наведено шляхом$dy=f'(3)\,dx$. Так як у$f'(x)=2x+2,$ нас

$dy=f'(3)\,dx=(2(3)+2)(0.1)=0.8.$

Вправа$\PageIndex{5}$

Для$y=x^2+2x,$ знахідки$Δy$ і$dy$$x=3$ при$dx=0.2.$

Підказка

$dy=f'(3)\,dx, \;Δy=f(3.2)−f(3)$

Відповідь

$dy=1.6, \; Δy=1.64$

Обчислення суми похибки

Будь-який тип вимірювання схильний до певної величини похибки. У багатьох додатках певні величини розраховуються на основі вимірювань. Наприклад, площа кола обчислюється шляхом вимірювання радіуса кола. Похибка вимірювання радіуса призводить до помилки в обчислюваному значенні площі. Тут ми розглянемо цей тип помилок і вивчимо, як диференціали можуть бути використані для оцінки помилки.

Розглянемо функцію$f$ з входом, яка є виміряною величиною. Припустимо, точне значення вимірюваної величини є$a$, але виміряне значення є$a+dx$. Ми говоримо, що похибка вимірювання є$dx$ (або$Δx$). В результаті виникає помилка в розрахунковій кількості$f(x)$. Цей тип помилки відомий як поширена помилка і задається

$$Δy=f(a+dx)−f(a). \nonumber$$

Оскільки всі вимірювання схильні до певної міри похибки, ми не знаємо точного значення вимірюваної величини, тому ми не можемо точно обчислити поширену похибку. Однак, враховуючи оцінку точності вимірювання, ми можемо використовувати диференціали для наближення поширеної похибки.$Δy.$ Зокрема, якщо$f$ це диференційовна функція в$a$, поширена похибка дорівнює

$$Δy≈dy=f'(a)\,dx. \nonumber$$

На жаль, ми не знаємо точної величини$a.$ Однак ми можемо використовувати виміряну величину$a+dx,$ і оцінити

$$Δy≈dy≈f'(a+dx)\,dx. \nonumber$$

У наступному прикладі ми розглянемо, як диференціали можуть бути використані для оцінки похибки обчислення обсягу коробки, якщо припустити, що вимірювання довжини сторони проводиться з певною точністю.

Приклад$\PageIndex{6}$: Volume of a Cube

Припустимо, довжина сторони куба вимірюється в$5$ см з точністю до$0.1$ см.

1. Використовуйте диференціали для оцінки похибки в обчисленому обсязі куба.
2. Обчисліть об'єм куба, якщо довжина сторони дорівнює (i)$4.9$ см і (ii)$5.1$ см, щоб порівняти оцінену похибку з фактичною потенційною похибкою.

Рішення

а Вимірювання довжини сторони є точним з точністю до$±0.1$ см. Тому,

$−0.1≤dx≤0.1.$

Обсяг куба задається$V=x^3$, що призводить до

$dV=3x^2dx.$

Використовуючи виміряну довжину сторони$5$ см, ми можемо оцінити, що

$−3(5)^2(0.1)≤dV≤3(5)^2(0.1).$

Тому,

$−7.5≤dV≤7.5.$

б. якщо довжина сторони фактично дорівнює$4.9$ см, то обсяг куба дорівнює

$V(4.9)=(4.9)^3=117.649\text{cm}^3.$

Якщо довжина сторони фактично дорівнює$5.1$ см, то обсяг куба дорівнює

$V(5.1)=(5.1)^3=132.651\text{cm}^3.$

Тому фактичний обсяг куба знаходиться між$117.649$ і$132.651$. Оскільки довжина сторони вимірюється рівною 5 см, обчислений об'єм$V(5)=5^3=125.$ Отже, похибка в обчислюваному обсязі дорівнює

$117.649−125≤ΔV≤132.651−125.$

Тобто,

$−7.351≤ΔV≤7.651.$

Ми бачимо, що$dV$ розрахункова похибка відносно близька до фактичної потенційної помилки в обчислюваному томі.

Вправа$\PageIndex{6}$

Оцініть похибку в обчисленому обсязі куба, якщо довжина сторони вимірюється в$6$ см з точністю до$0.2$ см.

Підказка

$dV=3x^2dx$

Відповідь

Вимірювання обсягу є точним в межах$21.6\,\text{cm}^3$.

Похибка вимірювання$dx\ (=Δx)$ та поширена похибка$Δy$ - абсолютні похибки. Нас, як правило, цікавить розмір похибки щодо розміру вимірюваної або обчислюваної кількості. З огляду на абсолютну$Δq$ похибку для певної величини, ми визначаємо відносну похибку як$\frac{Δq}{q}$, де$q$ - фактичне значення величини. Похибка у відсотках - відносна похибка, виражена у відсотках. Наприклад, якщо ми вимірюємо висоту сходів, щоб бути$63$ в. коли фактична висота знаходиться$62$ в., абсолютна похибка становить 1 дюйм. але відносна похибка є$\frac{1}{62}=0.016$, або$1.6\%$. Для порівняння, якщо ми вимірюємо ширину шматка картону, щоб бути$8.25$ в. коли фактична ширина$8$ в., наша абсолютна похибка знаходиться$\frac{1}{4}$ в., тоді як відносна похибка$\frac{0.25}{8}=\frac{1}{32}$, або$3.1\%.$ Отже, процентна похибка при вимірюванні картону більше, навіть хоча$0.25$ в. менше, ніж$1$ в.

Приклад$\PageIndex{7}$: Relative and Percentage Error

Астронавт за допомогою камери вимірює радіус Землі як$4000$ mi з похибкою$±80$ mi. Давайте використаємо диференціали для оцінки відносної та процентної похибки використання цього вимірювання радіуса для обчислення об'єму Землі, припускаючи, що планета є ідеальною сферою.

Рішення: Якщо вимірювання радіуса є точним в межах,$±80,$ ми маємо

$−80≤dr≤80.$

Оскільки обсяг сфери задається у$V=(\frac{4}{3})πr^3,$ нас є

$dV=4πr^2dr.$

Використовуючи виміряний радіус$4000$ mi, ми можемо оцінити

$−4π(4000)^2(80)≤dV≤4π(4000)^2(80).$

Щоб оцінити відносну похибку, розглянемо$\dfrac{dV}{V}$. Оскільки ми не знаємо точного значення обсягу$V$, використовуйте виміряний радіус$r=4000$ mi для оцінки$V$. Отримуємо$V≈(\frac{4}{3})π(4000)^3$. Тому відносна похибка задовольняє

$\frac{−4π(4000)^2(80)}{4π(4000)^3/3}≤\dfrac{dV}{V}≤\frac{4π(4000)^2(80)}{4π(4000)^3/3},$

що спрощує

$−0.06≤\dfrac{dV}{V}≤0.06.$

Відносна похибка є,$0.06$ а процентна похибка дорівнює$6\%$.

Вправа$\PageIndex{7}$

Визначте процентну похибку, якщо радіус Землі вимірюється$3950$ як mi з похибкою$±100$ mi.

Підказка

Використовуйте те, що$dV=4πr^2dr$ для пошуку$dV/V$.

Відповідь

$7.6\%$

Ключові концепції

• Диференційовна функція$y=f(x)$ може бути$a$ апроксимована за допомогою лінійної функції

$L(x)=f(a)+f'(a)(x−a).$

• Для функції$y=f(x)$, якщо$x$ змінюється з$a$ на$a+dx$, то

$dy=f'(x)\,dx$

є наближенням для зміни в$y$. Фактична зміна в$y$ є

$Δy=f(a+dx)−f(a).$

• Похибка вимірювання$dx$ може привести до помилки в розрахованій кількості$f(x)$. Похибка в обчислюваній кількості відома як поширена помилка. Розповсюджену помилку можна оцінити за

$dy≈f'(x)\,dx.$

• Для оцінки відносної похибки конкретної величини$q$ ми оцінюємо$\frac{Δq}{q}$.

Ключові рівняння

• Лінійне наближення

$L(x)=f(a)+f'(a)(x−a)$

• Диференціал

$dy=f'(x)\,dx$

Глосарій

диференціальний

диференціал$dx$ - це незалежна змінна, якій може бути присвоєно будь-яке ненульове дійсне число; диференціал$dy$ визначається як$dy=f'(x)\,dx$

диференціальна форма

задана$y=f'(x),$ диференційовна функція рівняння$dy=f'(x)\,dx$ є диференціальною формою похідної по$y$ відношенню до$x$

лінійне наближення

лінійна функція$L(x)=f(a)+f'(a)(x−a)$ - лінійне наближення$f$ at$x=a$

відсоток помилки

відносна похибка виражена у відсотках

поширена помилка

похибка, яка призводить до обчисленої кількості, що$f(x)$ виникає внаслідок похибки вимірювання$dx$

відносна помилка

задана абсолютна похибка$Δq$ для певної величини,$\frac{Δq}{q}$ є відносною похибкою.

наближення дотичної лінії (лінеаризація)

оскільки лінійне наближення$f$ at$x=a$ визначається за допомогою рівняння дотичної прямої, лінійне наближення$f$ at$x=a$ також відоме як наближення дотичної прямої до$f$ at$x=a$