7.4: Часткові дроби

Цілі навчання

• Інтегрувати раціональну функцію за допомогою методу часткових дробів.
• Розпізнавати прості лінійні фактори в раціональній функції.
• Розпізнавати повторювані лінійні фактори в раціональній функції.
• Розпізнавати квадратичні фактори в раціональній функції.

Ми бачили деякі методи, які дозволяють інтегрувати конкретні раціональні функції. Наприклад, ми знаємо, що

$$\int \dfrac{du}{u}=\ln |u|+C \nonumber$$

і

$$\int \dfrac{du}{u^2+a^2}=\dfrac{1}{a}\tan^{−1} \left(\dfrac{u}{a}\right)+C.\nonumber$$

Однак у нас ще немає техніки, яка дозволяє нам вирішувати довільні коефіцієнти цього типу. Таким чином, не відразу очевидно, як йти про оцінку

$$\int \dfrac{3x}{x^2−x−2}\,dx.\nonumber$$

Однак ми знаємо з раніше розробленого матеріалу, що

$$\int \left(\dfrac{1}{x+1}+\dfrac{2}{x−2}\right)\,dx=\ln |x+1|+2\ln |x−2|+C.\nonumber$$

Насправді, отримавши спільний знаменник, ми бачимо, що

$$\dfrac{1}{x+1}+\dfrac{2}{x−2}=\dfrac{3x}{x^2−x−2}.\nonumber$$

Отже,

$$\int \dfrac{3x}{x^2−x−2}\,dx=\int \left(\dfrac{1}{x+1}+\dfrac{2}{x−2}\right)\,dx.\nonumber$$

У цьому розділі розглянуто метод розкладання часткового дробу, який дозволяє розкласти раціональні функції на суми простих, легкоінтегрованих раціональних функцій. Використовуючи цей метод, ми можемо переписати такий вираз, як:

$$\dfrac{3x}{x^2−x−2}\nonumber$$

як такий вираз, як

$$\dfrac{1}{x+1}+\dfrac{2}{x−2}.\nonumber$$

Ключем до методу розкладання часткового дробу є можливість передбачити форму, яку прийме розкладання раціональної функції. Як ми побачимо, ця форма одночасно передбачувана і сильно залежить від факторизації знаменника раціональної функції. Також вкрай важливо мати на увазі, що часткове розкладання дробів може бути застосовано до раціональної функції$\dfrac{P(x)}{Q(x)}$ тільки в тому випадку, якщо$deg(P(x))<deg(Q(x))$. У разі коли$deg(P(x))≥deg(Q(x))$, ми повинні спочатку виконати довгий поділ, щоб переписати частку$\dfrac{P(x)}{Q(x)}$ в форму$A(x)+\dfrac{R(x)}{Q(x)}$, де$deg(R(x))<deg(Q(x))$. Потім ми робимо розкладання часткового дробу на$\dfrac{R(x)}{Q(x)}$. Наступний приклад, хоча і не вимагає розкладання часткового дробу, ілюструє наш підхід до інтегралів раціональних функцій виду$\int \dfrac{P(x)}{Q(x)}\,dx$, де$deg(P(x))≥deg(Q(x)).$

Приклад$\PageIndex{1}$: Integrating $\displaystyle \int \frac{P(x)}{Q(x)}\,dx$, where $deg(P(x))≥deg(Q(x))$

Оцінити

$$\int \dfrac{x^2+3x+5}{x+1}\,dx. \nonumber$$

Рішення

Так як$deg(x^2+3x+5)≥deg(x+1),$ ми виконуємо довгий поділ, щоб отримати

$$\dfrac{x^2+3x+5}{x+1}=x+2+\dfrac{3}{x+1}. \nonumber$$

Таким чином,

$$\int \dfrac{x^2+3x+5}{x+1}\,dx=\int \left(x+2+\dfrac{3}{x+1}\right)\,dx=\dfrac{1}{2}x^2+2x+3\ln |x+1|+C. \nonumber$$

Відвідайте цей веб-сайт для огляду довгого поділу поліномів.

Вправа$\PageIndex{1}$

Оцінити

$$\int \dfrac{x−3}{x+2}\,dx. \nonumber$$

Підказка

Використовуйте довге ділення для отримання$\dfrac{x−3}{x+2}=1−\dfrac{5}{x+2}. \nonumber$

Відповідь

$$x−5\ln |x+2|+C \nonumber$$

Щоб інтегрувати$\displaystyle \int \dfrac{P(x)}{Q(x)}\,dx$, де$deg(P(x))<deg(Q(x))$, ми повинні почати з факторингу$Q(x)$.

Неповторювані лінійні фактори

Якщо$Q(x)$ можна врахувати як$(a_1x+b_1)(a_2x+b_2)…(a_nx+b_n)$, де кожен лінійний фактор відрізняється, то можна знайти константи, що$A_1,A_2,…A_n$ задовольняють

$$\dfrac{P(x)}{Q(x)}=\dfrac{A_1}{a_1x+b_1}+\dfrac{A_2}{a_2x+b_2}+⋯+\dfrac{A_n}{a_nx+b_n}. \label{eq:7.4.1}$$

Доказ того, що такі константи існують, виходить за рамки цього курсу.

У наступному прикладі ми бачимо, як використовувати часткові дроби для інтеграції раціональної функції цього типу.

Приклад$\PageIndex{2}$: Partial Fractions with Nonrepeated Linear Factors

Оцінити$\displaystyle \int \dfrac{3x+2}{x^3−x^2−2x}\,dx.$

Рішення

Так як$deg(3x+2)<deg(x^3−x^2−2x)$, ми починаємо з факторингу знаменника$\dfrac{3x+2}{x^3−x^2−2x}$. Ми можемо це бачити$x^3−x^2−2x=x(x−2)(x+1)$. Таким чином, існують константи$A$$B$, і$C$ задовольняють Equation\ ref {eq:7.4.1} такі, що

$$\dfrac{3x+2}{x(x−2)(x+1)}=\dfrac{A}{x}+\dfrac{B}{x−2}+\dfrac{C}{x+1}. \nonumber$$

Тепер ми повинні знайти ці константи. Для цього ми починаємо з отримання спільного знаменника праворуч. Таким чином,

$$\dfrac{3x+2}{x(x−2)(x+1)}=\dfrac{A(x−2)(x+1)+Bx(x+1)+Cx(x−2)}{x(x−2)(x+1)}. \nonumber$$

Тепер встановлюємо чисельники рівні один одному, отримуючи

$$3x+2=A(x−2)(x+1)+Bx(x+1)+Cx(x−2).\label{Ex2Numerator}$$

Є дві різні стратегії знаходження коефіцієнтів$A$$B$, і$C$. Ми називаємо їх методом прирівнювання коефіцієнтів і методом стратегічного заміщення.

Стратегія перша: метод прирівнювання коефіцієнтів

Перепишіть рівняння$\ref{Ex2Numerator}$ у вигляді

$$3x+2=(A+B+C)x^2+(−A+B−2C)x+(−2A). \nonumber$$

Рівнянні коефіцієнти виробляють систему рівнянь

$$\begin{align*} A+B+C &=0 \\[4pt] −A+B−2C &= 3 \\[4pt] −2A &=2. \end{align*}$$

Щоб вирішити цю систему, ми спочатку спостерігаємо, що$−2A=2⇒A=−1.$ підстановка цього значення в перші два рівняння дає нам систему

$B+C=1$

$B−2C=2$.

Множення другого рівняння на$−1$ і додавання отриманого рівняння до першого дає

$−3C=1,$

що, в свою чергу, означає, що$C=−\dfrac{1}{3}$. Підстановка цього значення в рівняння$B+C=1$ дає результат$B=\dfrac{4}{3}$. Таким чином, рішення цих рівнянь дає$A=−1, B=\dfrac{4}{3}$, і$C=−\dfrac{1}{3}$.

Важливо зазначити, що система, вироблена цим методом, є послідовною тоді і лише тоді, коли ми правильно налаштували розкладання. Якщо система непослідовна, є помилка в нашому розкладанні.

Стратегія друга: метод стратегічного заміщення

Метод стратегічного заміщення заснований на припущенні, що ми правильно налаштували декомпозицію. Якщо розкладання налаштовано правильно, то повинні бути значення$A, B,$ і$C$ які задовольняють Рівняння$\ref{Ex2Numerator}$ для всіх значень$x$. Тобто це рівняння має бути вірним для будь-якого значення, яке$x$ ми дбаємо підставити в нього. Тому, вибираючи значення$x$ ретельно і підставляючи їх у рівняння, ми можемо знайти$A, B$, причому$C$ легко. Наприклад, якщо підставити$x=0$, рівняння зводиться до$2=A(−2)(1)$. Рішення для$A$ врожайності$A=−1$. Далі, підставляючи$x=2$, рівняння зводиться до$8=B(2)(3)$ або еквівалентно$B=4/3$. Останній, підставляємо$x=−1$ в рівняння і отримуємо$−1=C(−1)(−3).$ Розв'язування, ми маємо$C=−\dfrac{1}{3}$.

Важливо мати на увазі, що якщо ми спробуємо використовувати цей метод з розкладанням, яке було налаштовано неправильно, ми все одно можемо знайти значення для констант, але ці константи безглузді. Якщо ми вирішимо використовувати метод стратегічної заміщення, то непогано перевірити результат шляхом рекомбінування термінів алгебраїчно.

Тепер, коли у нас є значення$A, B,$ і$C,$ ми перепишемо оригінальний інтеграл:

$$\int \dfrac{3x+2}{x^3−x^2−2x}\,dx=\int \left(−\dfrac{1}{x}+\dfrac{4}{3}⋅\dfrac{1}{x−2}−\dfrac{1}{3}⋅\dfrac{1}{x+1}\right)\,dx. \nonumber$$

Оцінка інтеграла дає нам

$$\int \dfrac{3x+2}{x^3−x^2−2x}\,dx=−\ln |x|+\dfrac{4}{3}\ln |x−2|−\dfrac{1}{3}\ln |x+1|+C. \nonumber$$

У наступному прикладі ми інтегруємо раціональну функцію, в якій ступінь чисельника не менше ступеня знаменника.

Приклад$\PageIndex{3}$: Dividing before Applying Partial Fractions

Оцінити$\displaystyle \int \dfrac{x^2+3x+1}{x^2−4}\,dx.$

Рішення

Так як$deg(x^2+3x+1)≥deg(x^2−4),$ ми повинні виконувати довгий ділення многочленів. Це призводить до

$$\dfrac{x^2+3x+1}{x^2−4}=1+\dfrac{3x+5}{x^2−4} \nonumber$$

Далі виконуємо розкладання часткового дробу далі$\dfrac{3x+5}{x^2−4}=\dfrac{3x+5}{(x+2)(x−2)}$. У нас є

$$\dfrac{3x+5}{(x−2)(x+2)}=\dfrac{A}{x−2}+\dfrac{B}{x+2}. \nonumber$$

Таким чином,

$$3x+5=A(x+2)+B(x−2). \nonumber$$

Вирішуючи для$A$ і$B$ використовуючи будь-який метод, отримуємо$A=11/4$ і$B=1/4.$

Переписуючи оригінальний інтеграл, у нас є

$$\int \dfrac{x^2+3x+1}{x^2−4}\,dx=\int \left(1+\dfrac{11}{4}⋅\dfrac{1}{x−2}+\dfrac{1}{4}⋅\dfrac{1}{x+2}\right)\,dx. \nonumber$$

Оцінка інтеграла виробляє

$$\int \dfrac{x^2+3x+1}{x^2−4}\,dx=x+\dfrac{11}{4}\ln |x−2|+\dfrac{1}{4}\ln |x+2|+C. \nonumber$$

Як ми бачимо в наступному прикладі, можливо, можна застосувати техніку розкладання часткового дробу до нераціональної функції. Хитрість полягає в перетворенні нераціональної функції в раціональну функцію за допомогою підстановки.

Приклад$\PageIndex{4}$: Applying Partial Fractions after a Substitution

Оцінити$\displaystyle \int \dfrac{\cos x}{\sin^2x−\sin x}\,dx.$

Рішення

Давайте почнемо з дозволу$u=\sin x.$ Отже,$du=\cos x\,dx.$ Після внесення цих замін, у нас є

$$\int \dfrac{\cos x}{\sin^2x−\sin x}\,dx=\int \dfrac{du}{u^2−u}=\int \dfrac{du}{u(u−1)}. \nonumber$$

Застосування розкладання часткової фракції до$\dfrac{1}{u(u−1)}$ дає$\dfrac{1}{u(u−1)}=−\dfrac{1}{u}+\dfrac{1}{u−1}.$

Таким чином,

$$\int \dfrac{\cos x}{\sin^2x−\sin x}\,dx=−\ln |u|+\ln |u−1|+C=−\ln |\sin x|+\ln |\sin x−1|+C. \nonumber$$

Вправа$\PageIndex{2}$

Оцінити$\displaystyle \int \dfrac{x+1}{(x+3)(x−2)}\,dx.$

Підказка

$$\dfrac{x+1}{(x+3)(x−2)}=\dfrac{A}{x+3}+\dfrac{B}{x−2} \nonumber$$

Відповідь

$$\dfrac{2}{5}\ln |x+3|+\dfrac{3}{5}\ln |x−2|+C \nonumber$$

Повторні лінійні фактори

Для деяких застосувань нам потрібно інтегрувати раціональні вирази, які мають знаменники з повторюваними лінійними факторами - тобто раціональні функції з принаймні одним$n$ коефіцієнтом виду,$(ax+b)^n,$ де додатне ціле число більше або дорівнює$2$. Якщо знаменник містить повторюваний лінійний множник$(ax+b)^n$, то розкладання повинно містити

$$\dfrac{A_1}{ax+b}+\dfrac{A_2}{(ax+b)^2}+⋯+\dfrac{A_n}{(ax+b)^n}. \label{eq:7.4.2}$$

Як ми бачимо в нашому наступному прикладі, базова методика, яка використовується для розв'язування коефіцієнтів, однакова, але для визначення чисельників часткових дробів потрібно більше алгебри.

Приклад$\PageIndex{5}$: Partial Fractions with Repeated Linear Factors

Оцінити$\displaystyle \int \dfrac{x−2}{(2x−1)^2(x−1)}\,dx.$

Рішення

У нас є$deg(x−2)<deg((2x−1)^2(x−1)),$, щоб ми могли приступити до розкладання. Оскільки$(2x−1)^2$ є повторюваним лінійним коефіцієнтом, включають

$$\dfrac{A}{2x−1}+\dfrac{B}{(2x−1)^2} \nonumber$$

в розкладанні в Рівнянні\ ref {eq:7.4.2}. Таким чином,

$$\dfrac{x−2}{(2x−1)^2(x−1)}=\dfrac{A}{2x−1}+\dfrac{B}{(2x−1)^2}+\dfrac{C}{x−1}. \nonumber$$

Отримавши спільний знаменник і прирівнявши чисельники, маємо

$$x−2=A(2x−1)(x−1)+B(x−1)+C(2x−1)^2. \label{Ex5Numerator}$$

Потім ми використовуємо метод прирівнювання коефіцієнтів, щоб знайти значення$A, B,$ і$C$.

$$x−2=(2A+4C)x^2+(−3A+B−4C)x+(A−B+C). \nonumber$$

Прирівнюючі коефіцієнти прибутковості$2A+4C=0$$−3A+B−4C=1$,, і$A−B+C=−2$. Рішення цієї системи дає$A=2, B=3,$ і$C=−1.$

Як варіант, можна використовувати метод стратегічного заміщення. У цьому випадку підставляючи$x=1$ і$x=1/2$ в Рівняння$\ref{Ex5Numerator}$ легко виробляє значення$B=3$ і$C=−1$. На даний момент може здатися, що у нас закінчився хороший вибір$x$, однак, оскільки у нас вже є значення для$B$ і$C$, ми можемо замінити ці значення та вибрати будь-яке значення для раніше$x$ не використовуваного. Значення$x=0$ - непоганий варіант. У цьому випадку отримуємо рівняння$−2=A(−1)(−1)+3(−1)+(−1)(−1)^2$ або, що еквівалентно,$A=2.$

Тепер, коли у нас є значення для$A, B,$ і$C$, ми переписуємо початковий інтеграл і оцінюємо його:

\ [\ begin {align*}\ int\ dfrac {x−2} {(2x−1) ^2 (x−1)}\, dx &=\ int\ ліворуч (\ dfrac {2} {2x−1} +\ dfrac {3} {(2x−1) ^2} −\ dfrac {1} {x−1}\ праворуч)\ dx\ [4pt]
&=\ ln |2x−1|−\ dfrac {3} {2 (2x−1)}} −\ ln |x−1|+c.\ end {align*}\]

Вправа$\PageIndex{3}$

Налаштування розкладання часткового дробу для

$$\int \dfrac{x+2}{(x+3)^3(x−4)^2}\,dx. \nonumber$$

(Не вирішуйте для коефіцієнтів або не завершуйте інтеграцію.)

Підказка

Використовуйте метод вирішення проблем Приклад$\PageIndex{5}$ для керівництва.

Відповідь

$$\dfrac{x+2}{(x+3)^3(x−4)^2}=\dfrac{A}{x+3}+\dfrac{B}{(x+3)^2}+\dfrac{C}{(x+3)^3}+\dfrac{D}{(x−4)}+\dfrac{E}{(x−4)^2} \nonumber$$

Загальний метод

Тепер, коли ми починаємо отримувати уявлення про те, як працює техніка розкладання часткових дробів, давайте окреслимо основний метод у наступній стратегії вирішення проблем.

Стратегія розв'язання задач: декомпозиція часткового дробу

Щоб розкласти раціональну функцію$P(x)/Q(x)$, скористайтеся наступними кроками:

1. Переконайтеся, що$deg(P(x))<deg(Q(x)).$ Якщо ні, виконайте довгий поділ многочленів.
2. Фактор$Q(x)$ у добуток лінійних і незведених квадратичних факторів. Незведена квадратика - це квадратика, яка не має реальних нулів.
3. Якщо припустити$deg(P(x))<deg(Q(x)$, що фактори$Q(x)$ визначають форму розкладання$P(x)/Q(x).$
   1. Якщо$Q(x)$ можна врахувати як$(a_1x+b_1)(a_2x+b_2)…(a_nx+b_n)$, де кожен лінійний фактор відрізняється, то можна знайти константи, що$A_1,A_2,...A_n$ задовольняють $$\dfrac{P(x)}{Q(x)}=\dfrac{A_1}{a_1x+b_1}+\dfrac{A_2}{a_2x+b_2}+⋯+\dfrac{A_n}{a_nx+b_n}. \nonumber$$
   2. Якщо$Q(x)$ містить повторюваний лінійний коефіцієнт$(ax+b)^n$, то розкладання повинно містити $$\dfrac{A_1}{ax+b}+\dfrac{A_2}{(ax+b)^2}+⋯+\dfrac{A_n}{(ax+b)^n}. \nonumber$$
   3. Для кожного нескорочуваного квадратичного фактора,$ax^2+bx+c$ який$Q(x)$ містить, розкладання повинно включати $$\dfrac{Ax+B}{ax^2+bx+c}. \nonumber$$
   4. Для кожного повторюваного нескорочуваного квадратичного$(ax^2+bx+c)^n,$ фактора розкладання повинно включати $$\dfrac{A_1x+B_1}{ax^2+bx+c}+\dfrac{A_2x+B_2}{(ax^2+bx+c)^2}+⋯+\dfrac{A_nx+B_n}{(ax^2+bx+c)^n}. \nonumber$$
   5. Після того як відповідне розкладання визначено, вирішуйте для констант.
   6. Останній, перепишіть інтеграл в його розкладеному вигляді і оцініть його за допомогою раніше розроблених методик або формул інтеграції.

Прості квадратичні фактори

Тепер давайте розглянемо інтеграцію раціонального виразу, в якому знаменник містить нескорочуваний квадратичний множник. Нагадаємо, що квадратичне$ax^2+bx+c$ є незвідним, якщо не$ax^2+bx+c=0$ має реальних нулів - тобто якщо$b^2−4ac<0.$

Приклад$\PageIndex{6}$: Rational Expressions with an Irreducible Quadratic Factor

Оцінити

$$\int \dfrac{2x−3}{x^3+x}\,dx.\nonumber$$

Рішення

Так як$deg(2x−3)<deg(x^3+x),$ множник знаменник і приступаємо до часткового дробу розкладання. Так як$x^3+x=x(x^2+1)$ містить нескорочуваний квадратичний фактор$x^2+1$, включають$\dfrac{Ax+B}{x^2+1}$ як частину розкладання, разом з$\dfrac{C}{x}$ для лінійного члена$x$. Таким чином, розкладання має вигляд

$$\dfrac{2x−3}{x(x^2+1)}=\dfrac{Ax+B}{x^2+1}+\dfrac{C}{x}.\nonumber$$

Отримавши спільний знаменник і прирівнявши чисельники, отримаємо рівняння

$$2x−3=(Ax+B)x+C(x^2+1).\nonumber$$

Рішення для$A,B,$ і$C,$ ми отримуємо$A=3, B=2,$ і$C=−3.$

Таким чином,

$$\dfrac{2x−3}{x^3+x}=\dfrac{3x+2}{x^2+1}−\dfrac{3}{x}.\nonumber$$

Підставивши назад в інтеграл, отримуємо

\ [\ почати {вирівнювати*}\ int\ dfrac {2x−3} {x^3+x}\, дх &=\ int\ ліворуч (\ dfrac {3x+2} {x^2+1}} {x}\ праворуч)\, dx\ nonumber\\ [4pt]
&=3\ int\ dfrac {x} {x^2) +1}\, dx+2\ int\ dfrac {1} {x^2+1}\, dx−3\ int\ dfrac {1} {x}\, dx &\ текст {Розділити інтеграл}\\ [4pt]
&=\ dfrac {3} {2}\ ln x^2 +1+2\ tan^ {−1} x−3\ ln |x|+c. &\ text {Оцінити кожен інтеграл}\ end {align*}\]

Примітка: Ми можемо переписати$\ln ∣x^2+1∣=\ln (x^2+1)$, якщо ми хочемо зробити це, оскільки$x^2+1>0.$

Приклад$\PageIndex{7}$: Partial Fractions with an Irreducible Quadratic Factor

Оцінити$\displaystyle \int \dfrac{\,dx}{x^3−8}.$

Рішення: Ми можемо почати з факторингу$x^3−8=(x−2)(x^2+2x+4).$ Ми бачимо, що квадратичний коефіцієнт$x^2+2x+4$ є незменшеним, оскільки$2^2−4(1)(4)=−12<0.$ Використовуючи декомпозицію, описану в стратегії розв'язання задач, ми отримуємо

$$\dfrac{1}{(x−2)(x^2+2x+4)}=\dfrac{A}{x−2}+\dfrac{Bx+C}{x^2+2x+4}. \nonumber$$

Після отримання спільного знаменника і прирівнювання чисельників, це стає

$$1=A(x^2+2x+4)+(Bx+C)(x−2). \nonumber$$

Застосовуючи будь-який метод, отримуємо$A=\dfrac{1}{12},B=−\dfrac{1}{12},$ і$C=−\dfrac{1}{3}.$

Рерайтинг у$\int \dfrac{\,dx}{x^3−8},$ нас

$$\int \dfrac{\,dx}{x^3−8}=\dfrac{1}{12}\int \dfrac{1}{x−2}\,dx−\dfrac{1}{12}\int \dfrac{x+4}{x^2+2x+4}\,dx. \nonumber$$

Ми бачимо, що

$$\int \dfrac{1}{x−2}\,dx=\ln |x−2|+C,\nonumber$$

проте

$$\int \dfrac{x+4}{x^2+2x+4}\,dx \nonumber$$

вимагає трохи більше зусиль. Давайте почнемо з завершення квадрата,$x^2+2x+4$ щоб отримати

$$x^2+2x+4=(x+1)^2+3. \nonumber$$

Допускаючи$u=x+1$ і, отже,$du=\,dx,$ ми бачимо, що

\ [\ begin {align*}\ int\ dfrac {x+4} {x^2+2x+4}\, dx &=\ int\ dfrac {x+4} {(x+1) ^2+3}\, dx &\ text {завершити квадрат на знаменнику}\\ [4pt]
&=\ int\ dfrac {u+3} {u^2+3}\ du &\ текст {Заміна} u=x+1,\, x = u−1,\ текст {і} du = dx\\ [4pt]
&=\ int\ dfrac {u} {u^2+3 } du+\ int\ dfrac {3} {u^2+3} ду &\ текст {Розділити чисельник окремо}\\ [4pt]
&=\ dfrac {1} {2}\ ln u^2+3+\ dfrac {3} {\ sqrt {3}}\ tan^ {−1}\ dfrac {u} {\ sqrt {3}} +C & &\ text {Оцінити кожен інтеграл}\\ [4pt]
&=\ dfrac {1} {2}\ ln x^2+2x+4+\ sqrt {3}\ tan^ {−1}\ ліворуч (\ dfrac {x+1} {\ sqrt {3}}\ праворуч) +C & &\ text {Перепишіть з точки зору} x\ text {і спростити}\ end {align*}\]

Підставляючи назад в оригінальний інтеграл і спрощення дає

$$\int \dfrac{ \,dx}{x^3−8}=\dfrac{1}{12}\ln |x−2|−\dfrac{1}{24}\ln |x^2+2x+4|−\dfrac{\sqrt{3}}{12}\tan^{−1}\left(\dfrac{x+1}{\sqrt{3}}\right)+C. \nonumber$$

Тут знову ж таки, ми можемо скинути абсолютне значення, якщо ми хочемо зробити це, так як$x^2+2x+4>0$ для всіх$x$.

Приклад$\PageIndex{8}$: Finding a Volume

Знайдіть об'єм твердого тіла обертання, отриманого обертанням області, укладеної графіком$f(x)=\dfrac{x^2}{(x^2+1)^2}$ і осі x$[0,1]$ -над інтервалом навколо осі y.

Рішення

Почнемо з ескізу області, яку потрібно обернути (див. Малюнок$\PageIndex{1}$). З ескізу ми бачимо, що метод оболонки - хороший вибір для вирішення цієї проблеми.

Малюнок$\PageIndex{1}$: Ми можемо використовувати метод оболонки, щоб знайти обсяг обертання, отриманий обертанням області, показаної навколо$y$ -осі.

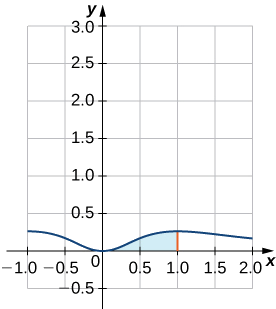
Обсяг задається

$$V=2π\int ^1_0x⋅\dfrac{x^2}{(x^2+1)^2}\,dx=2π\int ^1_0\dfrac{x^3}{(x^2+1)^2}\,dx. \nonumber$$

Так як можна$deg((x^2+1)^2)=4>3=deg(x^3),$ приступати до розкладання часткового дробу. Зверніть увагу, що$(x^2+1)^2$ це повторювана нескорочувана квадратика. Використовуючи декомпозицію, описану в стратегії розв'язання задач, отримаємо

$$\dfrac{x^3}{(x^2+1)^2}=\dfrac{Ax+B}{x^2+1}+\dfrac{Cx+D}{(x^2+1)^2}. \nonumber$$

Знаходження спільного знаменника і прирівнювання чисельників дає

$$x^3=(Ax+B)(x^2+1)+Cx+D. \nonumber$$

Вирішуючи, отримуємо$A=1, B=0, C=−1,$ і$D=0.$ підставляючи назад в інтеграл, ми маємо

$$V=2π\int _0^1\dfrac{x^3}{(x^2+1)^2}\,dx=2π\int _0^1\left(\dfrac{x}{x^2+1}−\dfrac{x}{(x^2+1)^2}\right)\,dx=2π\left(\dfrac{1}{2}\ln (x^2+1)+\dfrac{1}{2}⋅\dfrac{1}{x^2+1}\right)\Big|^1_0=π\left(\ln 2−\tfrac{1}{2}\right). \nonumber$$

Вправа$\PageIndex{4}$

Налаштування розкладання часткового дробу для $$\int \dfrac{x^2+3x+1}{(x+2)(x−3)^2(x^2+4)^2}\,dx. \nonumber$$

Підказка

Використовуйте стратегію вирішення проблем.

Відповідь

$$\dfrac{x^2+3x+1}{(x+2)(x−3)^2(x^2+4)^2}=\dfrac{A}{x+2}+\dfrac{B}{x−3}+\dfrac{C}{(x−3)^2}+\dfrac{Dx+E}{x^2+4}+\dfrac{Fx+G}{(x^2+4)^2} \nonumber$$

Ключові концепції

• Декомпозиція часткового дробу - це техніка, яка використовується для розбиття раціональної функції на суму простих раціональних функцій, які можуть бути інтегровані за допомогою раніше вивчених методів.
• Застосовуючи розкладання часткового дробу, ми повинні переконатися, що ступінь чисельника менше ступеня знаменника. Якщо ні, то нам потрібно виконати довгий ділення перед спробою розкладання часткового дробу.
• Форма, яку приймає розкладання, залежить від типу факторів в знаменнику. Типи факторів включають неповторювані лінійні фактори, повторювані лінійні фактори, неповторювані нескорочувані квадратичні фактори та повторювані незведені квадратичні фактори.

Глосарій

розкладання часткової фракції

метод, який використовується для розбиття раціональної функції на суму простих раціональних функцій