1.5: Експоненціальні та логарифмічні функції
- Page ID
- 62323
- Визначте форму експоненціальної функції.
- Поясніть різницю між графіками\(x^{b}\) і\(b^{x}\).
- Визнати значимість числа\(e\).
- Визначте форму логарифмічної функції.
- Поясніть зв'язок між експоненціальною та логарифмічною функціями.
- Опишіть, як обчислити логарифм до іншої основи.
- Визначте гіперболічні функції, їх графіки та основні ідентичності.
У цьому розділі ми розглянемо експоненціальні та логарифмічні функції. Ми використовуємо властивості цих функцій для розв'язання рівнянь за участю експоненціальних або логарифмічних термінів, вивчаємо значення і важливість числа\(e\). Також визначено гіперболічні та обернені гіперболічні функції, які включають комбінації експоненціальних та логарифмічних функцій. (Зауважте, що ми наводимо альтернативні визначення експоненціальних та логарифмічних функцій у розділі Програми інтеграцій та доведено, що функції мають однакові властивості з будь-яким визначенням.)
Експоненціальні функції
Експоненціальні функції виникають у багатьох додатках. Одним з поширених прикладів є зростання чисельності населення. Наприклад, якщо популяція починається з\(P_0\) особин, а потім зростає річними темпами\(2\%\), її популяція через 1 рік становить
\[P(1)=P_0+0.02P_0=P_0(1+0.02)=P_0(1.02).\nonumber \]
Його населення після 2 років становить
\[P(2)=P(1)+0.02P(1)=P(1)(1.02)=P_0(1.02)^2.\nonumber \]
Взагалі його популяція через\(t\) роки становить
\[P(t)=P_0(1.02)^t,\nonumber \]
яка є експоненціальною функцією. Більш загально, будь-яка функція виду\(f(x)=b^x\), де\(b>0\)\(b≠1\), є експоненціальною функцією з базовою\(b\) та експонентою\(x.\) Експоненціальні функції мають постійні основи та змінні показники. Зауважте, що функція виду\(f(x)=x^b\) для деякої константи не\(b\) є експоненціальною функцією, а силовою функцією.
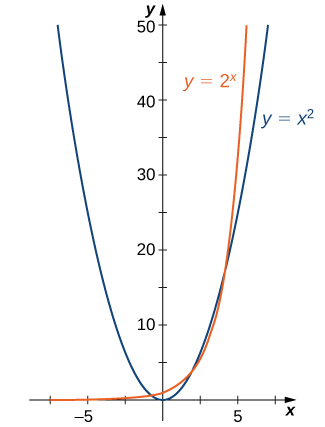
Щоб побачити різницю між експоненціальною функцією і силовою функцією, ми порівняємо функції\(y=x^2\) і\(y=2^x\). У таблиці ми бачимо\(\PageIndex{1}\), що обидва\(2^x\) і\(x^2\) наближаються до нескінченності як\(x→∞\). Врешті-решт, однак,\(2^x\) стає більшим, ніж\(x^2\) і росте швидше\(x→∞\). У зворотному напрямку, як\(x→−∞\)\(x^2→∞\), тоді як\(2^x→0\). Лінія\(y=0\) являє собою горизонтальну асимптоту для\(y=2^x\).
| \(x\) | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|---|---|---|
| \(x^2\) | 9 | 4 | 1 | 0 | 1 | 4 | 9 | 16 | 25 | 36 |
| \(2^x\) | 1/8 | 1/4 | 1/2 | 1 | 2 | 4 | 8 | 16 | 32 | 64 |
На малюнку\(\PageIndex{1}\) ми графуємо обидва\(y=x^2\) і\(y=2^x\) показуємо, чим відрізняються графіки.
Оцінка експоненціальних функцій
Нагадаємо властивості показників: Якщо\(x\) натуральне число, то визначаємо\(b^x=b⋅b⋯b\) (з\(x\) множниками\(b\)). Якщо\(x\) від'ємне ціле число, то\(x=−y\) для деякого позитивного цілого числа\(y\), і ми визначаємо\(b^x=b^{−y}=1/b^y\). Крім того,\(b^0\) визначається бути\(1\). Якщо\(x\) є раціональним числом, то\(x=p/q\), де\(p\) і\(q\) є цілими числами і\(b^x=b^{p/q}=\sqrt[q]{b^p}\). Наприклад,\(9^{3/2}=\sqrt{9^3}=\left(\sqrt{9}\right)^3=27\). Однак як\(b^x\) визначається, чи\(x\) є ірраціональним числом? Наприклад, що ми маємо на увазі\(2^{\sqrt{2}}\)? Це занадто складне питання, щоб ми могли повністю відповісти прямо зараз; однак, ми можемо зробити наближення.
| \(x\) | 1.4 | 1.41 | 1.414 | 1.4142 | 1.41421 | 1.414213 |
|---|---|---|---|---|---|---|
| \(2^x\) | 2.639 | 2.65737 | 2.66475 | 2.665119 | 2.665138 | 2.665143 |
У таблиці\(\PageIndex{2}\) наведено деякі раціональні числа\(\sqrt{2}\), що наближаються, а також\(x\) наведені значення\(2^x\) для кожного раціонального числа. Ми стверджуємо, що якщо ми вибираємо раціональні числа\(x\) все ближче і ближче до\(\sqrt{2}\), значення\(2^x\) стають все ближче і ближче до якогось числа\(L\). Ми визначаємо, що число\(L\) буде\(2^{\sqrt{2}}\).
Припустимо, певна популяція бактерій, як відомо, подвоюється в розмірі\(4\) щогодини. Якщо культура починається з\(1000\) бактерій, кількість бактерій після\(4\) години становить\(n(4)=1000⋅2\). Кількість бактерій в\(8\) неробочий час становить\(n(8)=n(4)⋅2=1000⋅2^2\). Загалом, кількість бактерій після\(4m\) години становить\(n(4m)=1000⋅2^m\). Відпускаючи\(t=4m\), ми бачимо, що кількість бактерій після t годин є\(n(t)=1000⋅2^{t/4}\). Знайдіть кількість бактерій після\(6\) годин,\(10\) годин та\(24\) годин.
Рішення
Кількість бактерій через 6 годин дається
\[n(6)=1000⋅2^{6/4}≈2828\, \text{bacteria}. \nonumber \]
Кількість бактерій в\(10\) неробочий час задається
\[n(10)=1000⋅2^{10/4}≈5657\, \text{bacteria}. \nonumber \]
Кількість бактерій в\(24\) неробочий час дають\(n(24)=1000⋅2^6=64,000\) бактерії.
З огляду на експоненціальну функцію\(f(x)=100⋅3^{x/2}\), оцінюють\(f(4)\) і\(f(10)\).
- Відповідь
-
\(f(4)=900\)
\(f(10)=24,300\).
Графічні експоненціальні функції
Для будь-якої бази\(b>0\) експоненціальна функція\(f(x)=b^x\) визначається для всіх дійсних чисел\(x\) і\(b^x>0\).\(b≠1\) Тому домен\(f(x)=b^x\) is\((−∞,∞)\) і діапазон є\((0,∞)\). Для графіка\(b^x\), відзначимо\(b>1\), що для,\(b^x\) збільшується на\((−∞,∞)\) і\(b^x→∞\) як\(x→∞\), тоді\(b^x→0\) як як\(x→−∞\). З іншого боку, якщо\(0<b<1\),\(f(x)=b^x\) зменшується на\((−∞,∞)\) і\(b^x→0\) як\(x→∞\) тоді,\(b^x→∞\) як\(x→−∞\) (рис.\(\PageIndex{2}\)).
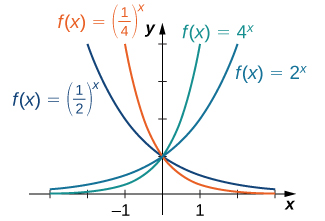
Зауважимо, що експоненціальні функції задовольняють загальним законам показників. Щоб нагадати вам про ці закони, ми визначимо їх як правила.
Для будь-яких констант\(a>0\)\(b>0\), і для всіх\(x\) і\(y,\)
- \[b^x⋅b^y=b^{x+y} \nonumber \]
- \[\dfrac{b^x}{b^y}=b^{x−y} \nonumber \]
- \[(b^x)^y=b^{xy} \nonumber \]
- \[(ab)^x=a^xb^x \nonumber \]
- \[\dfrac{a^x}{b^x}=\left(\dfrac{a}{b}\right)^x \nonumber \]
Використовуйте закони показників, щоб спростити кожне з наступних виразів.
- \(\dfrac{(2x^{2/3})^3}{(4x^{−1/3})^2}\)
- \(\dfrac{(x^3y^{−1})^2}{(xy^2)^{−2}}\)
Рішення
a. ми можемо спростити наступним чином:
\[\dfrac{(2x^{2/3})^3}{(4x^{−1/3})^2}=\dfrac{2^3(x^{2/3})^3}{4^2(x^{−1/3})^2}= \dfrac{8x^2}{16x^{−2/3}} =\dfrac{x^2x^{2/3}}{2}=\dfrac{x^{8/3}}{2}. \nonumber \]
б. ми можемо спростити наступним чином:
\[\dfrac{(x^3y^{−1})^2}{(xy^2)^{−2}}=\dfrac{(x^3)^2(y^{−1})^2}{x^{−2}(y^2)^{−2}}=\dfrac{x^6y^{−2}}{x^{−2}y^{−4}} =x^6x^2y^{−2}y^4=x^8y^2. \nonumber \]
Використовуйте закони експонентів для спрощення\(\dfrac{6x^{−3}y^2}{12x^{−4}y^5}\).
- Підказка
-
\(x^a/x^b=x^{a-b}\)
- Відповідь
-
\(x/(2y^3)\)
Число е
Особливий тип експоненціальної функції часто з'являється в реальних додатках. Для його опису розглянемо наступний приклад експоненціального зростання, який виникає внаслідок нарощування відсотків на ощадному рахунку. Припустимо, людина вкладає\(P\) долари на ощадний рахунок з річною процентною ставкою\(r\), що ускладнюється щорічно. Сума грошей після 1 року
\(A(1)=P+rP=P(1+r)\).
Сума грошей через\(2\) роки становить
\(A(2)=A(1)+rA(1)=P(1+r)+rP(1+r)=P(1+r)^2\).
Більш загально, сума через\(t\) роки становить
\(A(t)=P(1+r)^t\).
Якщо гроші складаються 2 рази на рік, сума грошей після півроку становить
\(A\left(\dfrac{1}{2}\right)=P+\left(\dfrac{r}{2}\right)P=P\left(1+\left(\dfrac{r}{2}\right)\right)\).
Сума грошей за\(1\) роком становить
\(A(1)=A\left(\dfrac{1}{2}\right)+\left(\dfrac{r}{2}\right)A \left(\dfrac{1}{2}\right)=P\left(1+\dfrac{r}{2}\right)+\dfrac{r}{2}\left(\left(P(1+\dfrac{r}{2}\right)\right)=P\left(1+\dfrac{r}{2}\right)^2.\)
Через\(t\) роки сума грошей на рахунку становить
\(A(t)=P\left(1+\dfrac{r}{2}\right)^{2t}\).
Більш загально, якщо гроші складаються\(n\) раз на рік, сума грошей на рахунку через\(t\) роки дається функцією
\(A(t)=P\left(1+\dfrac{r}{n}\right)^{nt}.\)
Що відбувається як\(n→∞?\) Щоб відповісти на це питання, давайте\(m=n/r\) і пишемо
\(\left(1+\dfrac{r}{n}\right)^{nt}=\left(1+\dfrac{1}{m}\right)^{mrt},\)
і вивчити поведінку\((1+1/m)^m\) as\(m→∞\), використовуючи таблицю значень (Таблиця\(\PageIndex{3}\)).
| \(m\) | 10 | 100 | 1000 | 10 000 | 100 000 | 1 000 000 |
|---|---|---|---|---|---|---|
| \(\left(1+\dfrac{1}{m}\right)^m\) | 2.5937 | 2.7048 | 2.71692 | 2.71815 | 2.718268 | 2.718280 |
Дивлячись на цю таблицю, виявляється, що\((1+1/m)^m\) наближається число між\(2.7\) і\(2.8\) як\(m→∞\). Насправді,\((1+1/m)^m\) наближається до деякого числа, як\(m→∞\). Дзвонимо за цим номером\(e\). До шести знаків після коми точності
\[e≈2.718282. \nonumber \]
Лист вперше\(e\) був використаний для представлення цього числа швейцарським математиком Леонардом Ейлером протягом 1720-х років. Хоча Ейлер не виявив числа, він показав багато важливих зв'язків між\(e\) і логарифмічними функціями. Ми все ще використовуємо позначення\(e\) сьогодні, щоб вшанувати роботу Ейлера, оскільки вона з'являється у багатьох областях математики і тому, що ми можемо використовувати її у багатьох практичних застосуваннях.
Повертаючись до нашого прикладу ощадного рахунку, можна зробити висновок, що якщо людина ставить\(P\) долари на рахунок під річну процентну ставку\(r\), що посилюється безперервно, то\(A(t)=Pe^{rt}\). Ця функція може бути знайома. Оскільки функції за участю бази\(e\) виникають часто в додатках, ми називаємо функцію\(f(x)=e^x\) природною експоненціальною функцією. Не тільки ця функція цікава через визначення числа\(e\), але і, як обговорювалося далі, її графік має важливу властивість.
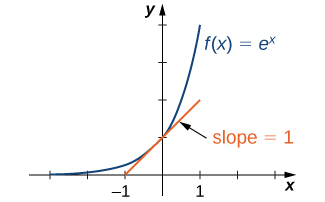
З тих пір\(e>1\), як ми знаємо\(f(x) = e^x\), збільшується на\((−∞,∞)\). На малюнку\(\PageIndex{3}\) ми показуємо графік\(f(x)=e^x\) разом з дотичною лінією до графіка\(f\) at\(x=0\). Ми даємо точне визначення дотичної лінії в наступному розділі; але, неофіційно, ми говоримо, що дотична лінія до графіка\(f\) at\(x=a\) - це лінія, яка проходить через точку\((a,f(a))\) і має такий же «нахил», що і\(f\) в цій точці. Функція\(f(x)=e^x\) є єдиною\(b^x\) експоненціальною функцією з дотичною лінією при\(x=0\) цьому має нахил\(1.\) Як ми бачимо пізніше в тексті, маючи цю властивість робить природну експоненціальну функцію найпростішою експоненціальною функцією для використання у багатьох випадках.
Припустимо,\($500\) вкладається в рахунок за річною процентною ставкою\(r=5.5\%\), що складається безперервно.
- Нехай\(t\) позначають кількість років після початкових вкладень і\(A(t)\) позначають суму грошей на рахунку в момент часу\(t\). Знайдіть формулу для\(A(t)\).
- Знайти суму грошей на рахунку через\(10\) роки і після\(20\) років.
Рішення
а Якщо\(P\) долари інвестуються в рахунок за річною процентною ставкою\(r\), що складається безперервно, то\(A(t)=Pe^{rt}\). Ось\(P=$500\) і\(r=0.055\). Тому,\(A(t)=500e^{0.055t}\).
б. через\(10\) роки сума грошей на рахунку дорівнює
\(A(10)=500e^{0.055⋅10}=500e^{0.55}≈$866.63\).
Через\(20\) роки сума грошей на рахунку становить
\(A(20)=500e^{0.055⋅20}=500e^{1.1}≈$1,502.08\).
Якщо\($750\) вкладається в рахунок під річну процентну ставку\(4\%\), що складається безперервно, знайдіть формулу для суми грошей на рахунку через\(t\) роки. Знайти суму грошей через\(30\) роки.
- Підказка
-
\(A(t)=Pe^{rt}\)
- Відповідь
-
\(A(t)=750e^{0.04t}\). Через\(30\) роки буде приблизно\($2,490.09\).
Логарифмічні функції
Використовуючи наше розуміння експоненціальних функцій, ми можемо обговорити їх зворотні, які є логарифмічними функціями. Вони стануть в нагоді, коли нам потрібно розглянути будь-яке явище, яке змінюється в широкому діапазоні значень, наприклад, шкала рН в хімії або децибел в рівнях звуку.
Експоненціальна функція\(f(x)=b^x\) один до одного, з доменом\((−∞,∞)\) і діапазоном\((0,∞)\). Тому він має обернену функцію, звану логарифмічною функцією з основою\(b\). Для будь-якого\(b>0,\, b≠1\) логарифмічна функція з базою\(b\), позначається\(\log_b\), має область\((0,∞)\) і діапазон\((−∞,∞)\), і задовольняє
\[\log_b(x)=y \nonumber \]
якщо і тільки якщо\(b^y=x\).
Наприклад,
\[\log_2(8)=3\nonumber \]
так як\(2^3=8\),
\[\log_{10}\left(\dfrac{1}{100}\right)=−2 \nonumber \]
так як\(10^{−2}=\dfrac{1}{10^2}=\dfrac{1}{100}\),
\[\log_b(1)=0 \nonumber \]
так як\(b^0=1\) для будь-якої бази\(b>0\).
Крім того, оскільки\(y=\log_b(x)\) і\(y=b^x\) є зворотними функціями,
\[\log_b(b^x)=x \nonumber \]
і
\[b^{\log_b(x)}=x. \nonumber \]
Найбільш часто використовуваною логарифмічною функцією є функція\(\log_e\). Оскільки ця функція використовує натуральне в\(e\) якості своєї основи, її називають натуральним логарифмом. Тут ми використовуємо позначення\(\ln (x)\) або\(\ln x\) для позначення\(\log_e(x)\). Наприклад,
\[ \begin{align*} \ln (e) &=\log_e(e)=1 \\[4pt] \ln (e^3) &=\log_e(e^3)=3 \\[4pt] \ln (1) &=\log_e(1)=0. \end{align*}\]
Так як функції\(f(x)=e^x\) і\(g(x)=\ln (x)\) є оберненнями один одного,
\(\ln (e^x)=x\)і\(e^{\ln x}=x\),
і їх графіки симетричні щодо лінії\(y=x\) (рис.\(\PageIndex{4}\)).
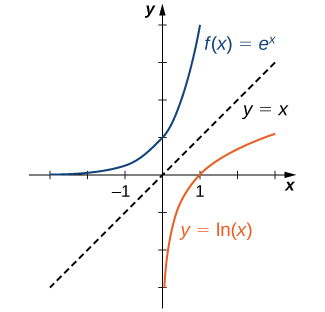
Загалом, для будь-якої бази\(b>0\) функція\(g(x)=\log_b(x)\) симетрична щодо лінії\(y=x\) з функцією\(f(x)=b^x\).\(b≠1\) Використовуючи цей факт і графіки експоненціальних функцій, ми графуємо функції\(\log_b\) для декількох значень\(b>1\) (рис.\(\PageIndex{5}\)).
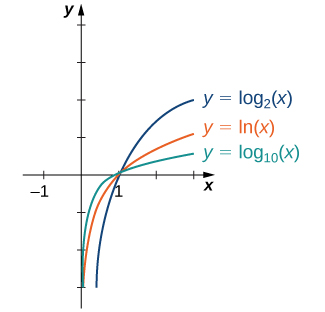
Перш ніж розв'язувати деякі рівняння, що включають експоненціальні та логарифмічні функції, розглянемо основні властивості логарифмів.
Якщо\(a,\,b,\,c>0,\,b≠1\), і\(r\) є будь-яким дійсним числом, то
- Властивість продукту
\[\log_b(ac)=\log_b(a)+\log_b(c) \label{productprop} \]
- Часткове майно
\[\log_b \left(\dfrac{a}{c} \right)=\log_b(a)−\log_b(c) \label{quotientprop} \]
- Власне майно
\[\log_b(a^r)=r\log_b(a) \label{powerprop} \]
Вирішіть кожне з наступних рівнянь для\(x\).
- \(5^x=2\)
- \(e^x+6e^{−x}=5\)
Рішення
а Застосовуючи функцію натурального логарифма до обох сторін рівняння, ми маємо
\(\ln 5^x=\ln 2\).
Використовуючи властивість power логарифмів,
\(x\ln 5=\ln 2.\)
Тому,
\[x= \dfrac{\ln 2}{\ln 5}. \nonumber \]
б. множивши обидві сторони рівняння на\(e^x\), приходимо до рівняння
\(e^{2x}+6=5e^x\).
Переписування цього рівняння як
\(e^{2x}−5e^x+6=0\),
потім ми можемо переписати його як квадратне рівняння в\(e^x\):
\((e^x)^2−5(e^x)+6=0.\)
Тепер ми можемо вирішити квадратне рівняння. Факторинг цього рівняння отримаємо
\((e^x−3)(e^x−2)=0.\)
Тому рішення задовольняють\(e^x=3\) і\(e^x=2\). Прийняття натурального логарифму обох сторін дає нам рішення\(x=\ln 3,\ln 2\).
Вирішити
\[e^{2x}/(3+e^{2x})=1/2. \nonumber \]
- Підказка
-
Спочатку розв'яжіть рівняння для\(e^{2x}\)
- Відповідь
-
\(x=\dfrac{\ln 3}{2}\).
Вирішіть кожне з наступних рівнянь для\(x\).
- \(\ln \left(\dfrac{1}{x}\right)=4\)
- \(\log_{10}\sqrt{x}+\log_{10}x=2\)
- \(\ln (2x)−3\ln (x^2)=0\)
Рішення
а. за визначенням функції натурального логарифма,
\(\ln \left(\dfrac{1}{x} \right)=4\)
- якщо і тільки якщо\(e^4=\dfrac{1}{x}\).
Тому рішення є\(x=1/e^4\).
b Використовуючи добуток (Equation\ ref {productprop}) і потужність (Equation\ ref {powerprop}) властивостей логарифмічних функцій, перепишіть ліву частину рівняння як
\[\begin{align*} \log_{10}\sqrt{x} + \log_{10}x &= \log_{10} x \sqrt{x} \\[4pt] &= \log_{10}x^{3/2} \\[4pt] &= \dfrac{3}{2}\log_{10}x. \end{align*}\]
Тому рівняння можна переписати як
\(\dfrac{3}{2}\log_{10}x=2\)
або
\(\log_{10}x=\dfrac{4}{3}\).
Рішення є\(x=10^{4/3}=10\sqrt[3]{10}\).
c Використовуючи властивість power (Equation\ ref {powerprop}) логарифмічних функцій, ми можемо переписати рівняння як\(\ln (2x)−\ln (x^6)=0\).
Використовуючи часткову властивість (Equation\ ref {quotientprop}), це стає
\(\ln \left(\dfrac{2}{x^5}\right)=0\)
Тому\(2/x^5=1\), що має на увазі\(x=\sqrt[5]{2}\). Потім слід перевірити наявність сторонніх рішень.
Вирішити\(\ln (x^3)−4\ln (x)=1\).
- Підказка
-
Спочатку використовуйте властивість power, потім використовуйте властивість добутку логарифмів.
- Відповідь
-
\(x=\dfrac{1}{e}\)
При оцінці логарифмічної функції калькулятором ви, можливо, помітили, що єдиними варіантами є\(\log_{10}\) або\(\log\), званий загальним логарифмом, або\(\ln\), який є натуральним логарифмом. Однак експоненціальні функції та логарифмові функції можуть бути виражені через будь-яку бажану базу\(b\). Якщо вам потрібно скористатися калькулятором для оцінки виразу з іншою базою, ви можете спочатку застосувати формули зміни основи. Використовуючи цю зміну бази, ми зазвичай пишемо задану експоненціальну або логарифмічну функцію з точки зору натуральної експоненціальної та натуральної логарифмічної функцій.
Нехай\(a>0,\,b>0\), і\(a≠1,\,b≠1\).
1. \(a^x=b^{x \log_ba}\)для будь-якого дійсного числа\(x\).
Якщо\(b=e\), це рівняння зводиться до\(a^x=e^{x \log_ea}=e^{x \ln a}\).
2. \(\log_ax=\dfrac{\log_bx}{\log_ba}\)для будь-якого дійсного числа\(x>0\).
Якщо\(b=e\), це рівняння зводиться до\(\log_ax=\dfrac{\ln x}{\ln a}\).
Для першої зміни базової формули ми починаємо з використання властивості power логарифмічних функцій. Ми знаємо, що для будь-якої бази\(b>0,\, b≠1\),\(\log_b(a^x)=x \log_ba\). Тому,
\(b^{\log_b(a^x)}\)=\(b^{x \log_ba}\).
Крім того, ми знаємо, що\(b^x\) і\(\log_b(x)\) є зворотними функціями. Тому,
\(b^{\log_b(a^x)}=a^x\).
Поєднуючи ці останні дві рівності, робимо висновок, що\(a^x=b^{x \log_ba}\).
Щоб довести другу властивість, покажемо, що
\((\log_ba)⋅(\log_ax)=\log_bx.\)
Нехай\(u=\log_ba,v=\log_ax\), і\(w=\log_bx\). Ми це покажемо\(u⋅v=w\). За визначенням логарифмічних функцій ми знаємо\(b^u=a,\, a^v=x\), що, і\(b^w=x\). З попередніх рівнянь ми бачимо, що
\(b^{uv}=(b^u)^v=a^v=x=b^w.\)
Тому,\(b^{uv}=b^w\). Оскільки експоненціальні функції є один до одного, можна зробити висновок, що\(u⋅v=w\).
\(\square\)
Використовуйте обчислювальну утиліту для оцінки\(\log_37\) за формулою зміни основи, представленої раніше.
Рішення
Використовуйте друге рівняння з\(a=3\) і\(b=e\):\(\log_37=\dfrac{\ln 7}{\ln 3}≈1.77124\).
Використовуйте формулу зміни бази та обчислювальну корисність для оцінки\(\log_46\).
- Підказка
-
Скористайтеся зміною бази, щоб переписати цей вираз через вирази, що включають функцію натурального логарифма.
- Відповідь
-
\(\log_46 = \dfrac{\ln 6}{\ln 4} \approx 1.29248\)
У 1935 році Чарльз Ріхтер розробив шкалу (тепер відома як шкала Ріхтера) для вимірювання магнітуди землетрусу. Шкала являє собою логарифмічну шкалу база-10, і її можна описати наступним чином: Розглянемо один землетрус магнітудою\(R_1\) за шкалою Ріхтера і другий землетрус з магнітудою\(R_2\) за шкалою Ріхтера. Припустимо\(R_1>R_2\), що означає землетрус магнітудою\(R_1\) сильніше, але наскільки він сильніший за інший землетрус?

Спосіб вимірювання інтенсивності землетрусу полягає у використанні сейсмографа для вимірювання амплітуди хвиль землетрусу. Якщо\(A_1\) амплітуда, виміряна для першого землетрусу, і\(A_2\) є амплітудою, виміряною для другого землетрусу, то амплітуди і величини двох землетрусів задовольняють наступному рівнянню:
\(R_1−R_2=\log_{10}\left(\dfrac{A1}{A2}\right)\).
Розглянемо землетрус, який вимірює 8 за шкалою Ріхтера і землетрус, який вимірює 7 за шкалою Ріхтера. Потім,
\(8−7=\log_{10}\left(\dfrac{A1}{A2}\right)\).
Тому,
\(\log_{10}\left(\dfrac{A1}{A2}\right)=1\),
що має на увазі\(A_1/A_2=10\) або\(A_1=10A_2\). \(A_1\)Оскільки в 10 разів більше\(A_2\), ми говоримо, що перший землетрус в 10 разів інтенсивніше другого землетрусу. З іншого боку, якщо один землетрус вимірює 8 за шкалою Ріхтера, а інший вимірює 6, то відносна інтенсивність двох землетрусів задовольняє рівнянню.
\(\log_{10}\left(\dfrac{A1}{A2}\right)=8−6=2\).
Отже,\(A_1=100A_2\) .Тобто перший землетрус в 100 разів інтенсивніше другого.
Як ми можемо використовувати логарифмічні функції для порівняння відносної тяжкості землетрусу магнітудою 9 магнітудою в Японії в 2011 році з землетрусом магнітудою 7,3 на Гаїті в 2010 році?
Рішення
Щоб порівняти землетруси в Японії та Гаїті, ми можемо використовувати рівняння, представлене раніше:
\(9−7.3=\log_{10}\left(\dfrac{A1}{A2}\right)\).
Тому і робимо висновок\(A_1/A_2=10^{1.7}\), що землетрус в Японії був приблизно в 50 разів інтенсивніше, ніж землетрус на Гаїті.
Порівняйте відносну тяжкість\(8.4\) землетрусу магнітудою з магнітудою\(7.4\) землетрусу.
- Підказка
-
\(R_1−R_2=\log_{10}(A1/A2)\).
- Відповідь
-
\(8.4\)Землетрус магнітудою приблизно\(10\) в рази важкий, ніж\(7.4\) землетрус магнітудою.
Гіперболічні функції
Гіперболічні функції визначаються з точки зору певних комбінацій\(e^x\) і\(e^{−x}\). Ці функції виникають природно в різних інженерно-фізичних додатках, включаючи вивчення водних хвиль і коливань пружних мембран. Іншим поширеним використанням гіперболічної функції є подання висячого ланцюга або кабелю, також відомого як контактний зв'язок (рис.\(\PageIndex{7}\)). Якщо ввести систему координат так, щоб нижня точка ланцюга лежала уздовж\(y\) -осі, ми можемо описати висоту ланцюга в терміні гіперболічної функції. Спочатку визначаємо гіперболічні функції.

Гіперболічний косинус
\(\cosh x=\dfrac{e^x+e^{−x}}{2}\)
гіперболічний синус
\(\sinh x=\dfrac{e^x−e^{−x}}{2}\)
Гіперболічний тангенс
\(\tanh x=\dfrac{\sinh x}{\cosh x}=\dfrac{e^x−e^{−x}}{e^x+e^{−x}}\)
Гіперболічний косеканс
\(\operatorname{csch}x=\dfrac{1}{\sinh x}=\dfrac{2}{e^x−e^{−x}}\)
Гіперболічний секантний
\(\operatorname{sech}x=\dfrac{1}{\cosh x}=\dfrac{2}{e^x+e^{−x}}\)
Гіперболічний котангенс
\(\coth x=\dfrac{\cosh x}{\sinh x}=\dfrac{e^x+e^{−x}}{e^x−e^{−x}}\)
Назва\(\cosh\) римується з «гош», тоді як назва\(\sinh\) вимовляється «cinch». \(\operatorname{Tanh}, \,\operatorname{sech}, \, \operatorname{csch},\)і\(\coth\) вимовляються «танч», «мова», «комова» і «котанч» відповідно.
Використовуючи визначення\(\cosh(x)\) і принципи фізики, можна показати, що висота висить ланцюга, така як та, яка на малюнку\(\PageIndex{8}\), може бути описана функцією\(h(x)=a\cosh(x/a) + c\) для певних констант\(a\) і\(c\).
Але чому ці функції називаються гіперболічними функціями? Щоб відповісти на це питання, розглянемо кількість\(\cosh^2 t − \sinh^2 t\). Використовуючи визначення\(\cosh\) і\(\sinh\), ми бачимо, що
\[\cosh^2 t − \sinh^2 t=\dfrac{e^{2t}+2+e^{−2t}}{4}−\dfrac{e^{2t}−2+e^{−2t}}{4}=1. \nonumber \]
Ця ідентичність є аналогом тригонометричної ідентичності\(\cos^2 t + \sin^2 t=1\). Тут при заданому\(t\) значенні точка\((x,y)=(\cosh t,\,\sinh t)\) лежить на одиниці гіперболи\(x^2−y^2=1\) (рис.\(\PageIndex{8}\)).
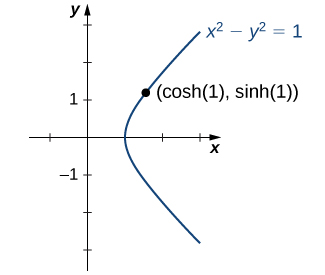
Графіки гіперболічних функцій
Для графіка\(\cosh x\) і\(\sinh x\), ми використовуємо той факт, що обидві функції підходять\((1/2)e^x\) як\(x→∞\), так\(e^{−x}→0\) як як\(x→∞\). Як\(x→−∞,\cosh x\) підходи\(1/2e^{−x}\), тоді як\(\sinh x\) підходи\(−1/2e^{−x}\). Тому, використовуючи графіки\(1/2e^x,1/2e^{−x}\), і в\(−1/2e^{−x}\) якості орієнтирів, графуємо\(\cosh x\) і\(\sinh x\). Для\(\tanh x\) графування ми використовуємо той факт\(\tanh(0)=0\), що,\(−1<\tanh(x)<1\) для всіх\(x\),\(\tanh x→1\) як\(x→∞\), і\(\tanh x→−1\) як\(x→−∞\). Графіки інших трьох гіперболічних функцій можуть бути намальовані за допомогою графіків\(\cosh x\)\(\sinh x\), і\(\tanh x\) (рис.\(\PageIndex{9}\)).
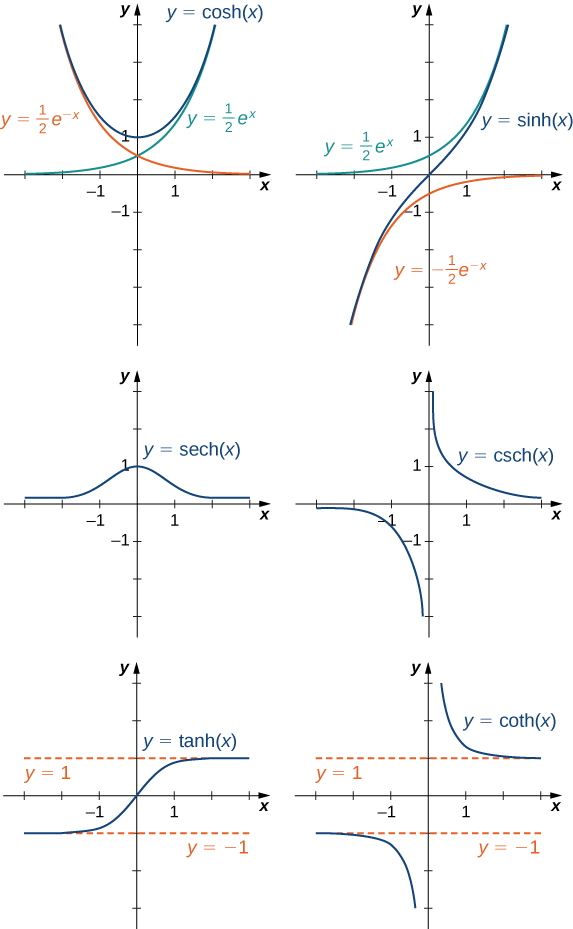
Ідентичності за участю гіперболічних функцій
Ідентичність\(\cosh^2 t−\sinh^2 t = 1\), показана на малюнку\(\PageIndex{8}\), є однією з декількох тотожностей, що включають гіперболічні функції, деякі з яких перераховані далі. Перші чотири властивості легко випливають з визначень гіперболічного синуса та гіперболічного косинуса. За винятком деяких відмінностей у знаках, більшість цих властивостей аналогічні ідентичностям для тригонометричних функцій.
- \(\cosh(−x)=\cosh x\)
- \(\sinh(−x)=−\sinh x\)
- \(\cosh x+\sinh x=e^x\)
- \(\cosh x−\sinh x=e^{−x}\)
- \(\cosh^2 x−\sinh^2 x=1\)
- \(1−\tanh^2 x=\operatorname{sech}^2 x\)
- \(\coth^2 x −1=\operatorname{csch}^2 x\)
- \(\sinh(x±y)=\sinh x \cosh y ± \cosh x \sinh y\)
- \(\cosh(x±y)=\cosh x \cosh y ± \sinh x \sinh y\)
- Спростити\(\sinh(5\ln x)\).
- Якщо\(\sinh x=3/4\), знайти значення інших п'яти гіперболічних функцій.
Рішення:
a. використовуючи визначення\(\sinh\) функції, пишемо
\(\sinh(5\ln x)=\dfrac{e^{5\ln x}−e^{−5\ln x}}{2}=\dfrac{e^{\ln (x^5)}−e^{\ln (x^{−5})}}{2}=\dfrac{x^5−x^{−5}}{2}.\)
b Використовуючи ідентичність\(\cosh^2 x − \sinh^2 x=1\), ми бачимо, що
\(\cosh^2 x=1+\left(\frac{3}{4}\right)^2=\dfrac{25}{16}.\)
Так як\(\cosh x≥1\) для всіх\(x\) ми повинні мати\(\cosh x=5/4\). Потім, використовуючи визначення для інших гіперболічних функцій, робимо висновок, що\(\tanh x=3/5,\operatorname{csch}x=4/3,\operatorname{sech}x=4/5\), і\(\coth x=5/3\).
Спростити\(\cosh(2\ln x)\).
- Підказка
-
Використовують визначення\(\cosh\) функції та степеневу властивість функцій логарифма.
- Відповідь
-
\((x^2+x^{−2})/2\)
Обернені гіперболічні функції
З графіків гіперболічних функцій ми бачимо, що всі вони один до одного крім\(\cosh x\) і\(\operatorname{sech}x\). Якщо обмежити області цих двох функцій інтервалом,\([0,∞),\) то всі гіперболічні функції є один до одного, і ми можемо визначити зворотні гіперболічні функції. Оскільки самі гіперболічні функції включають експоненціальні функції, обернені гіперболічні функції включають логарифмічні функції.
\ [\ почати {align*} &\ sinh^ {−1} x =\ ім'я оператора {arcsing} x=\ n\ ліворуч (x+\ sqrt {x^2+1}\ праворуч) &\ cosh^ {−1} x =\ ім'я оператора {arccosh} x =\ ln\ ліворуч (x+\ sqrt {x^2−1}\ праворуч)\ [4pt]
&\ tanh^ {−1} x=\ ім'я оператора {арктан} x =\ dfrac {1} {2}\ ln\ ліворуч (\ dfrac {1+x} {1−x}\ праворуч) &\ coth^ {−1} x =\ ім'я оператора {arccot} x =\ frac {1} {2}\ ln\ ліворуч (\ dfrac {x+1} {x−1}\ праворуч)\\ [4pt]
&\ ім'я оператора {sech} ^ {−1} x=\ ім'я оператора {arcsech} x =\ ln\ ліворуч (\ dfrac {1+\ sqrt {1x−^2}} {x}\ праворуч) &\ ім'я оператора {csch} ^ {−1} x =\ ім'я оператора {arcscch} x =\ ln\ ліворуч (\ dfrac {1} {x} +\ dfrac {\ sqrt {1+x^2}} {|x|}\ праворуч)\ кінець { вирівнювати*}\]
Давайте розглянемо, як вивести перше рівняння. Інші слідують аналогічно. Припустимо\(y=\sinh^{−1}x\). Потім,\(x=\sinh y\) і, за визначенням гіперболічної синусоїдальної функції,\(x=\dfrac{e^y−e^{−y}}{2}\). Тому,
\(e^y−2x−e^{−y}=0.\)
Помноживши це рівняння на\(e^y\), отримаємо
\(e^{2y}−2xe^y−1=0\).
Це можна вирішити як квадратне рівняння, з розв'язком
\(e^y=\dfrac{2x±\sqrt{4x^2+4}}{2}=x±\sqrt{x^2+1}\).
Так як\(e^y>0\), єдиним рішенням є той, що має позитивний знак. Застосовуючи натуральний логарифм до обох сторін рівняння, робимо висновок, що
\(y=\ln (x+\sqrt{x^2+1}).\)
Оцінити кожне з наведених нижче виразів.
\(\sinh^{−1}(2)\)
\(\tanh^{−1}(1/4)\)
Рішення:
\[\sinh^{−1}(2)=\ln (2+\sqrt{2^2+1})=\ln (2+\sqrt{5})≈1.4436\nonumber \]
\[\tanh^{−1}(1/4)=\frac{1}{2}\ln \left(\dfrac{1+1/4}{1−1/4}\right)=\frac{1}{2}\ln \left(\dfrac{5/4}{3/4}\right)=\frac{1}{2}\ln \left(\dfrac{5}{3}\right)≈0.2554\nonumber \]
Оцініть\(\tanh^{−1}(1/2)\).
- Підказка
-
Скористайтеся визначенням\(\tanh^{−1}x\) і спрощуйте.
- Відповідь
-
\(\dfrac{1}{2}\ln (3)≈0.5493\).
Ключові поняття
- Експоненціальна функція\(y=b^x\) збільшується if\(b>1\) і зменшується if\(0<b<1\). Його домен є\((−∞,∞)\) і його діапазон є\((0,∞)\).
- Логарифмічна функція\(y=\log_b(x)\) є оберненою\(y=b^x\). Його домен є,\((0,∞)\) а його діапазон\((−∞,∞).\)
- Природна експоненціальна функція є,\(y=e^x\) а природна логарифмічна функція дорівнює\(y=\ln x=\log_ex.\)
- З огляду на експоненціальну функцію або логарифмічну функцію в базі\(a\), ми можемо зробити зміну бази, щоб перетворити цю функцію в будь-яку базу\(b>0\),\(b≠1.\) Ми зазвичай перетворюємо на базу\(e\).
- Гіперболічні функції включають комбінації експоненціальних функцій\(e^x\) і в\(e^{−x}.\) результаті обернені гіперболічні функції включають природний логарифм.
Глосарій
- база
- число\(b\) в експоненціальній функції\(f(x)=b^x\) та логарифмічна функція\(f(x)=\log_bx\)
- показник
- значення\(x\) у виразі\(b^x\)
- гіперболічні функції
- функції позначаються\(\sinh,\,\cosh,\,\operatorname{tanh},\,\operatorname{csch},\,\operatorname{sech},\) і\(\coth\), які передбачають певні комбінації\(e^x\) і\(e^{−x}\)
- обернені гіперболічні функції
- зворотні гіперболічні функції де\(\cosh\) і\( \operatorname{sech}\) обмежені доменом\([0,∞)\); кожна з цих функцій може бути виражена через склад натуральної логарифмової функції та алгебраїчної функції
- природна експоненціальна функція
- функція\(f(x)=e^x\)
- натуральний логарифм
- функція\(\ln x=\log_ex\)
- число е
- як\(m\) стає більше, кількість\((1+(1/m)^m\) наближається до деякого дійсного числа; ми визначаємо, що дійсне число буде\(e;\)\(e\) значенням приблизно\(2.718282\)
