1.4: Зворотні функції
- Page ID
- 62340
- Визначте умови, коли функція має зворотну.
- Використовуйте тест горизонтальної лінії, щоб розпізнати, коли функція є один до одного.
- Знайти обернену задану функцію.
- Намалюйте графік оберненої функції.
- Оцініть обернені тригонометричні функції.
Зворотна функція змінює операцію, виконану певною функцією. Іншими словами, що б функція не робила, обернена функція скасовує її. У цьому розділі формально визначимо обернену функцію та визначимо необхідні умови існування оберненої функції. Розглянуто, як знайти обернену функцію та вивчаємо зв'язок між графом функції та графом її оберненої. Потім ми застосовуємо ці ідеї для визначення та обговорення властивостей обернених тригонометричних функцій.
Існування оберненої функції
Почнемо з прикладу. Враховуючи функцію\(f\) та вихід\(y=f(x)\), ми часто зацікавлені в тому, щоб знайти, яке значення або значення\(x\) були\(y\) зіставлені\(f\). Для прикладу розглянемо функцію\(f(x)=x^3+4\). Оскільки будь-який вихід\(y=x^3+4\), ми можемо вирішити це рівняння для\(x\) того, щоб знайти, що вхід є\(x=\sqrt[3]{y−4}\). Це рівняння визначає\(x\) як функцію\(y\). Позначивши цю функцію як\(f^{−1}\), так і пишемо\(x=f^{−1}(y)=\sqrt[3]{y−4}\), ми бачимо, що для будь-якої\(x\) в області\(f,f^{−1}\)\(f(x))=f^{−1}(x^3+4)=x\). Таким чином, ця нова функція\(f^{−1}\), «скасувала» те, що зробила оригінальна функція\(f\). Функція з цією властивістю називається оберненою функцією початкової функції.
Враховуючи функцію\(f\) з доменом\(D\) та діапазоном\(R\), її обернена функція (якщо вона існує) є функцією\(f^{−1}\) з доменом\(R\) та діапазоном\(D\) таких, що\(f^{−1}(y)=x\) якщо і тільки якщо\(f(x)=y\). Іншими словами, для функції\(f\) та її зворотного\(f^{−1}\),
\[f^{−1}(f(x))=x \nonumber \]
для всіх\(x\) в\(D\) і
\[f(f^{−1}(y))=y \nonumber \]
для всіх\(y\) в\(R\).
Зверніть увагу, що\(f^{−1}\) читається як «\(f\)зворотний». Тут не\(−1\) використовується як показник, тому
\[f^{−1}(x)≠ \dfrac{1}{f(x)}. \nonumber \]
\(\PageIndex{1}\)На малюнку показано взаємозв'язок між доменом і діапазоном,\(f\) а також доменом і діапазоном\(f^{−1}\).
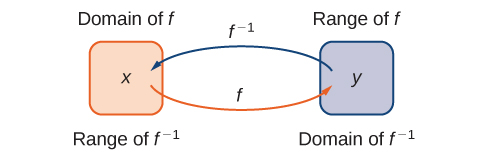
Нагадаємо, що функція має рівно один вихід для кожного входу. Тому, щоб визначити обернену функцію, нам потрібно зіставляти кожен вхід точно на один вихід. Для прикладу спробуємо знайти обернену функцію для\(f(x)=x^2\). Вирішуючи рівняння\(y=x^2\) для\(x\), приходимо до рівняння\(x=±\sqrt{y}\). Це рівняння не описується\(x\) як функція,\(y\) тому що існує два рішення цього рівняння для кожного\(y>0\). Проблема з спробою знайти обернену функцію для\(f(x)=x^2\) полягає в тому, що два входи надсилаються на один і той же вихід для кожного виходу\(y>0\). \(f(x)=x^3+4\)Розглянута раніше функція не мала цієї проблеми. Для цієї функції кожен вхід був відправлений на інший вихід. Функція, яка надсилає кожен вхід на інший вихід, називається функцією один до одного.
Ми говоримо, що функція\(f\) є один до одного функція, якщо\(f(x_1)≠f(x_2)\) коли\(x_1≠x_2\).
Один із способів визначити, чи є функція один до одного, - це дивлячись на її графік. Якщо функція один-на-один, то на один і той же вихід не можна надсилати два входи. Тому, якщо ми намалюємо горизонтальну лінію в будь-якому місці\(xy\) -площині, згідно з тестом горизонтальної лінії, вона не може перетинати графік більше одного разу. Відзначимо, що тест горизонтальної лінії відрізняється від тесту вертикальної лінії. Тест вертикальної лінії визначає, чи є графік графіком функції. Тест горизонтальної лінії визначає, чи є функція один-на-один (рис.\(\PageIndex{2}\)).
Функція\(f\) є один до одного тоді і тільки тоді, коли кожна горизонтальна лінія перетинає графік\(f\) не більше одного разу.
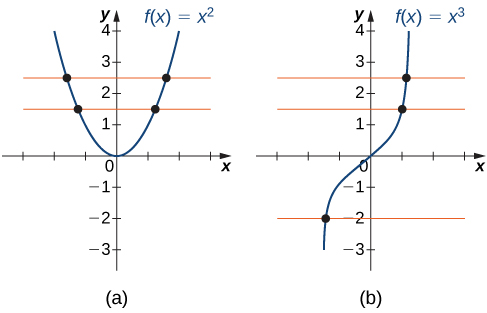
Для кожної з наступних функцій використовуйте тест горизонтальної лінії, щоб визначити, чи є він один до одного.
а)
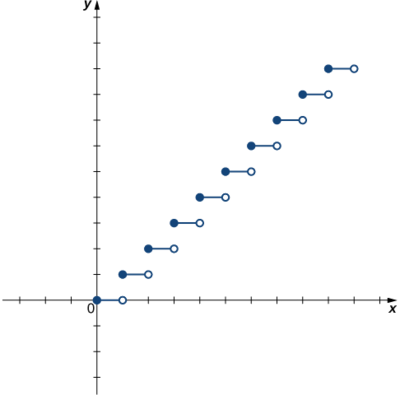
б)
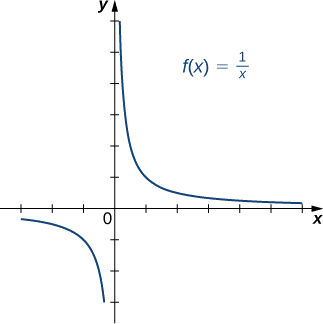
Рішення
а) Оскільки горизонтальна лінія\(y=n\) для будь-якого цілого числа\(n≥0\) перетинає графік більше одного разу, ця функція не є один-до-одному.
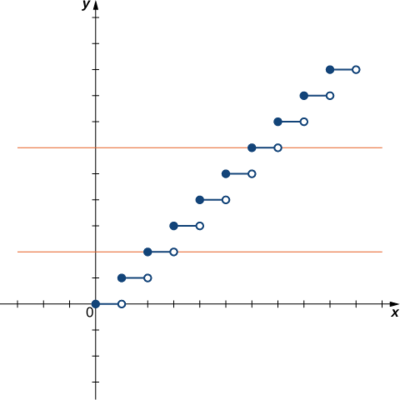
б) Оскільки кожна горизонтальна лінія перетинає графік один раз (максимум), ця функція є один до одного.
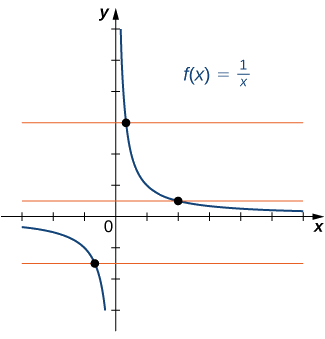
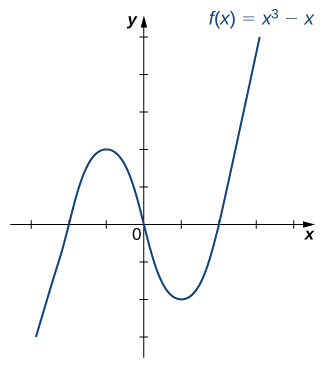
Чи є функція\(f\) графіком на наступному зображенні один до одного?
- Рішення
-
Використовуйте тест горизонтальної лінії.
- Відповідь
-
Ні
Пошук оберненої функції
Тепер ми можемо розглянути функції один-на-один і показати, як знайти їх зворотні. Нагадаємо, що функція відображає елементи\(f\) в області двох елементів в діапазоні\(f\). Зворотна функція відображає кожен елемент з діапазону\(f\) назад до відповідного елемента з області\(f\). Тому, щоб знайти обернену функцію один-до-одному\(f\), задану будь-яку\(y\) в діапазоні\(f\), нам потрібно визначити, яка\(x\) в області\(f\) задовольняє\(f(x)=y\). Так як\(f\) один до одного, існує рівно одне таке значення\(x\). Ми можемо знайти це значення,\(x\) вирішивши рівняння\(f(x)=y\) для\(x\). Роблячи це, ми можемо записати\(x\) як функцію,\(y\) де область цієї функції є діапазоном,\(f\) а діапазон цієї нової функції є областю\(f\). Отже, ця функція обернена\(f\), і ми пишемо\(x=f^{−1}(y)\). Оскільки ми зазвичай використовуємо змінну\(x\) для позначення незалежної змінної і y для позначення залежної змінної, ми часто обмінюємося ролями\(x\) і\(y\), і писати\(y=f^{−1}(x)\). Представлення зворотної функції таким чином також корисно пізніше, коли ми графуємо функцію\(f\) та її зворотну\(f^{−1}\) на тих же осях.
- Розв'яжіть рівняння\(y=f(x)\) для\(x\).
- Поміняйте змінні\(x\)\(y\) і запишіть\(y=f^{−1}(x)\).
Знайти обернену для функції\(f(x)=3x−4.\) State область та діапазон оберненої функції. Переконайтеся, що\(f^{−1}(f(x))=x.\)
Рішення
Дотримуйтесь кроків, викладених у стратегії.
Крок 1. Якщо\(y=3x−4,\) тоді\(3x=y+4\) і\(x=\frac{1}{3}y+\frac{4}{3}.\)
Крок 2. Перепишіть як\(y=\frac{1}{3}x+\frac{4}{3}\) і\(y=f^{−1}(x)\) нехай\(f^{−1}(x)=\frac{1}{3}x+\frac{4}{3}\). Тому.
Оскільки домен\(f\) є\((−∞,∞)\), діапазон\(f^{−1}\) є\((−∞,∞)\). Оскільки діапазон\(f\) є\((−∞,∞)\), домен\(f^{−1}\) є\((−∞,∞)\).
Ви можете переконатися, що\(f^{−1}(f(x))=x\) написавши
\(f^{−1}(f(x))=f^{−1}(3x−4)=\frac{1}{3}(3x−4)+\frac{4}{3}=x−\frac{4}{3}+\frac{4}{3}=x.\)
Зауважте, що for\(f^{−1}(x)\) бути оберненою\(f(x)\), як\(f^{−1}(f(x))=x\) і\(f(f^{−1}(x))=x\) для всіх\(x\) в області внутрішньої функції.
Знайдіть обернену функцію\(f(x)=3x/(x−2)\). Вкажіть область та діапазон оберненої функції.
- Підказка
-
Використовувати стратегію вирішення проблем для пошуку обернених функцій.
- Відповідь
-
\(f^{−1}(x)=\dfrac{2x}{x−3}\). Домен\(f^{−1}\) is\(\{x\,|\,x≠3\}\). В асортименті\(f^{−1}\) є\(\{y\,|\,y≠2\}\).
Графік обернених функцій
Розглянемо зв'язок між графіком функції\(f\) і графіком її оберненої. Розглянемо графік,\(f\) показаний на малюнку,\(\PageIndex{3}\) і точку\((a,b)\) на графіку. З тих пір\(b=f(a)\)\(f^{−1}(b)=a\). Тому, коли ми\(f^{−1}\) графуємо, точка\((b,a)\) знаходиться на графіку. В результаті граф\(f^{−1}\) являє собою відображення графіка\(f\) близько прямої\(y=x\).
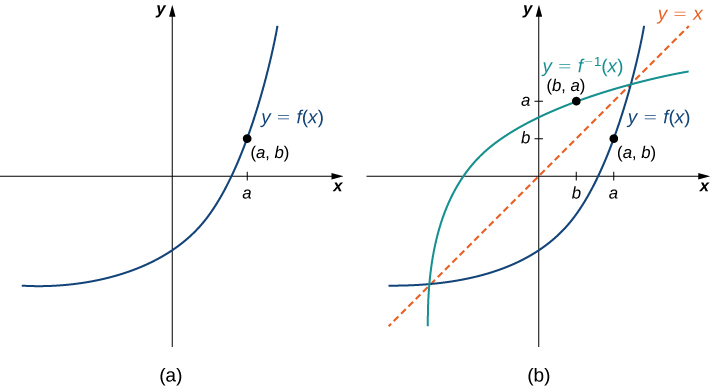
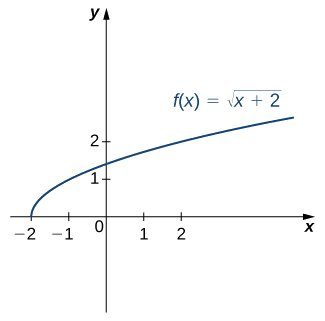
Для графіка на\(f\) наступному зображенні намалюйте графік,\(f^{−1}\) накидаючи лінію\(y=x\) та використовуючи симетрію. Визначте домен і діапазон\(f^{−1}\).
Рішення
Відобразіть графік навколо прямої\(y=x\). Домен\(f^{−1}\) is\([0,∞)\). В асортименті\(f^{−1}\) є\([−2,∞)\). Використовуючи попередню стратегію пошуку обернених функцій, ми можемо перевірити, чи є зворотна функція\(f^{−1}(x)=x^2−2\), як показано на графіку.
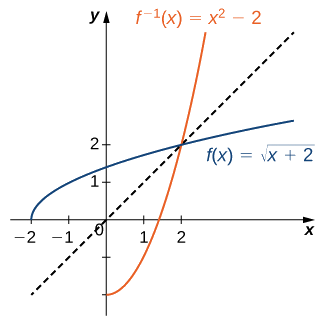
Намалюйте графік\(f(x)=2x+3\) та графік його зворотного за допомогою властивості симетрії обернених функцій.
- Підказка
-
Графіки симетричні щодо прямої\(y=x\)
- Відповідь
-
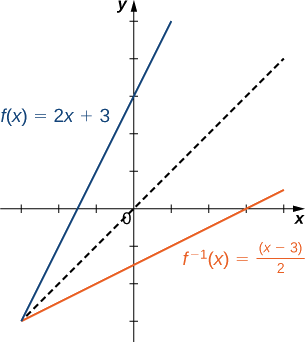
Обмеження доменів
Як ми бачили,\(f(x)=x^2\) не має зворотної функції, оскільки вона не є один-на-один. Однак ми можемо вибрати підмножину домену\(f\) такої, щоб функція була один-на-один. Ця підмножина називається обмеженим доменом. Обмежуючи домен\(f\), ми можемо визначити нову функцію,\(g\) таку, що домен\(g\) є обмеженим доменом\(f\) і\(g(x)=f(x)\) для всіх\(x\) у домені\(g\). Тоді ми можемо визначити обернену функцію для\(g\) цього домену. Наприклад, оскільки\(f(x)=x^2\) є один до одного на інтервалі\([0,∞)\), ми можемо визначити нову функцію,\(g\) таку, що домен\(g\) є\([0,∞)\) і\(g(x)=x^2\) для всіх\(x\) у своїй області. Оскільки\(g\) є функцією один до одного, вона має обернену функцію, задану формулою\(g^{−1}(x)=\sqrt{x}\). З іншого боку, функція також\(f(x)=x^2\) є один-на-один на домені\((−∞,0]\). Тому ми могли б також визначити нову функцію,\(h\) таку, що домен\(h\) є\((−∞,0]\) і\(h(x)=x^2\) для всіх\(x\) в області\(h\). Тоді\(h\) є функцією один до одного і також повинен мати зворотну. Його зворотний задається формулою\(h^{−1}(x)=−\sqrt{x}\) (рис.\(\PageIndex{4}\)).
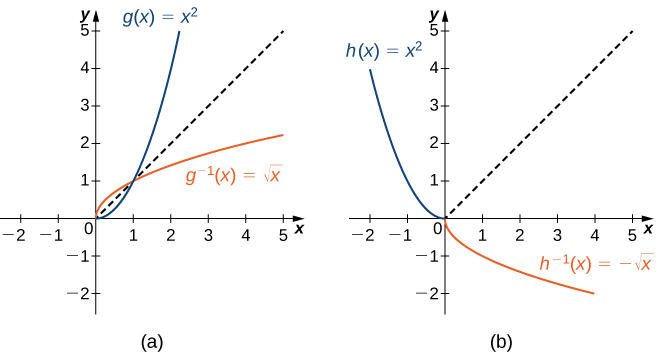
Розглянемо функцію\(f(x)=(x+1)^2\).
- Намалюйте графік\(f\) і використовуйте тест горизонтальної лінії, щоб показати, що\(f\) це не один до одного.
- Показати, що\(f\) це один-на-один на обмежений домен\([−1,∞)\). Визначте домен і діапазон для зворотного\(f\) на цьому обмеженому домені і знайдіть формулу для\(f^{−1}\).
Рішення
а) Графік\(f\) - це графік\(y=x^2\) зсунутої лівої\(1\) одиниці. Так як існує горизонтальна лінія, що\(f\) перетинає графік більше одного разу, не один до одного.
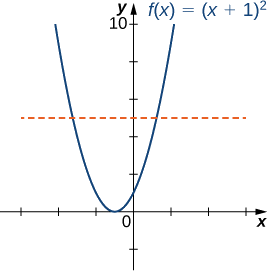
б) На інтервалі\([−1,∞),\;f\) один до одного.
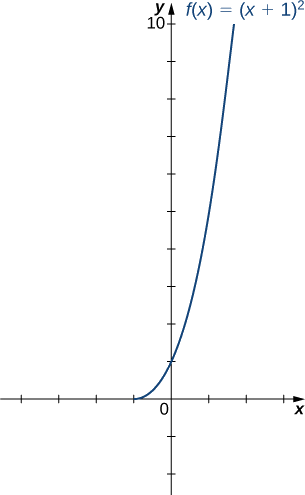
Домен і діапазон\(f^{−1}\) задаються діапазоном і\(f\) доменом відповідно. Таким чином, домен\(f^{−1}\) is\([0,∞)\) і діапазон\(f^{−1}\) is\([−1,∞)\). Щоб знайти формулу для\(f^{−1}\), розв'яжіть рівняння\(y=(x+1)^2\) для\(x.\) If\(y=(x+1)^2\), то\(x=−1±\sqrt{y}\). Так як ми обмежуємо домен інтервалом де\(x≥−1\), нам потрібно\(±\sqrt{y}≥0\). Тому,\(x=−1+\sqrt{y}\). \(x\)Поміняючись і\(y\), пишемо\(y=−1+\sqrt{x}\) і робимо висновок, що\(f^{−1}(x)=−1+\sqrt{x}\).
Розглянемо\(f(x)=1/x^2\) обмеження домену\((−∞,0)\). Переконайтеся, що\(f\) це один до одного на цьому домені. Визначте область і діапазон зворотного\(f\) і знайдіть формулу для\(f^{−1}\).
- Підказка
-
Домен і діапазон\(f^{−1}\) задаються діапазоном і\(f\) доменом відповідно. Знайти\(f^{−1}\), вирішувати\(y=1/x^2\) за\(x\).
- Відповідь
-
Домен\(f^{−1}\) is\((0,∞)\). В асортименті\(f^{−1}\) є\((−∞,0)\). Обернена функція задається формулою\(f^{−1}(x)=−1/\sqrt{x}\).
Обернені тригонометричні функції
Шість основних тригонометричних функцій є періодичними, і тому вони не є один-на-один. Однак, якщо ми обмежимо область тригонометричної функції інтервалом, де вона одна до одного, ми можемо визначити її зворотну. Розглянемо функцію синуса. Функція синуса є один до одного на нескінченній кількості інтервалів, але стандартна угода полягає в обмеженні домену інтервалом\(\left[−\frac{π}{2},\frac{π}{2}\right]\). Таким чином, ми визначаємо функцію зворотного синуса на області\([−1,1]\) таким чином, що для будь-якого\(x\) в інтервалі функція зворотного синуса говорить нам\([−1,1]\), який кут\(θ\) в інтервалі\(\left[−\frac{π}{2},\frac{π}{2}\right]\) задовольняє\(\sin θ=x\). Аналогічно, ми можемо обмежити області інших тригонометричних функцій для визначення обернених тригонометричних функцій, які є функціями, які говорять нам, який кут в певному інтервалі має задане тригонометричне значення.
Функція зворотного синуса, що позначається\(\sin^{−1}\) або\(\arcsin\), і функція зворотного косинуса, що позначається\(\cos^{−1}\) або\(\arccos\), визначаються в області\(D=\{x|−1≤x≤1\}\) наступним чином:
\(\sin^{−1}(x)=y\)
- якщо і тільки якщо\(\sin(y)=x\) і\(−\frac{π}{2}≤y≤\frac{π}{2}\);
\(\cos^{−1}(x)=y\)
- якщо і тільки якщо\(\cos(y)=x\) і\(0≤y≤π\).
Обернена тангенсна функція, що позначається\(\tan^{−1}\) або\(\arctan\), і обернена функція котангенса, що позначається\(\cot^{−1}\) або\(\operatorname{arccot}\), визначаються в області\(D=\{x|−∞<x<∞\}\) наступним чином:
\(\tan^{−1}(x)=y\)
- якщо і тільки якщо\(\tan(y)=x\) і\(−\frac{π}{2}<y<\frac{π}{2}\);
\(\cot^{−1}(x)=y\)
- якщо і тільки якщо\(\cot(y)=x\) і\(0<y<π\).
Зворотна косекансна функція, позначена\(\csc^{−1}\) або\(\operatorname{arccsc}\), і зворотна секантна функція, що позначається\(\sec^{−1}\) або\(\operatorname{arcsec}\), визначаються в області\(D=\{x\,|\,|x|≥1\}\) наступним чином:
\(\csc^{−1}(x)=y\)
- якщо і тільки якщо\(\csc(y)=x\) і\(−\frac{π}{2}≤y≤\frac{π}{2}, \, y≠0\);
\(\sec^{−1}(x)=y\)
- якщо і тільки якщо\(\sec(y)=x\) і\(0≤y≤π, \, y≠π/2\).
Для побудови графіків обернених тригонометричних функцій ми використовуємо графіки тригонометричних функцій, обмежених доменами, визначеними раніше, і відображаємо графіки про пряму\(y=x\) (рис.\(\PageIndex{5}\)).
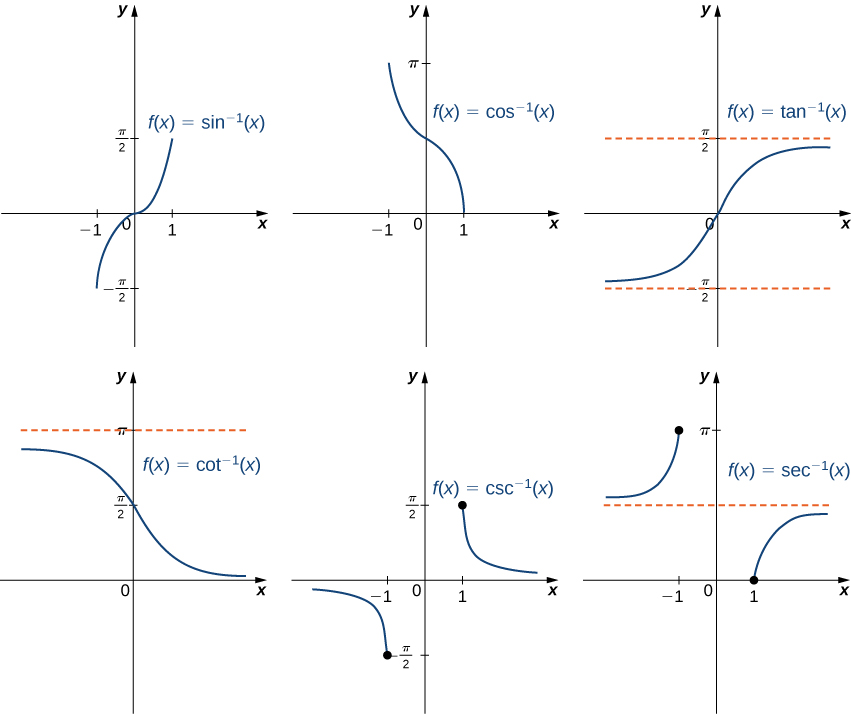
При оцінці оберненої тригонометричної функції виходом є кут. Наприклад, щоб оцінити\(\cos^{−1}\left(\frac{1}{2}\right)\), нам потрібно знайти\(θ\) такий кут, який\(\cos θ=\frac{1}{2}\). Зрозуміло, що багато кутів мають цю властивість. Однак, з огляду на визначення\(\cos^{−1}\), нам потрібен кут,\(θ\) який не тільки вирішує це рівняння, але і лежить в інтервалі\([0,π]\). Ми робимо висновок, що\(\cos^{−1}\left(\frac{1}{2}\right)=\frac{π}{3}\).
Розглянемо тепер склад тригонометричної функції і її зворотний. Наприклад, розглянемо два вирази\(\sin\left(\sin^{−1}\left(\frac{\sqrt{2}}{2}\right)\right)\) і\(\sin^{−1}(\sin(π)).\)
Для першого спрощуємо наступним чином:
\[\sin\left(\sin^{−1}\left(\frac{\sqrt{2}}{2}\right)\right)=\sin\left(\frac{π}{4}\right)=\frac{\sqrt{2}}{2}.\nonumber \]
Для другого у нас є
\[\sin^{−1}(\sin(π))=\sin^{−1}(0)=0.\nonumber \]
Зворотна функція повинна «скасувати» вихідну функцію, так чому б не\(\sin^{−1}(\sin(π))=π?\) Згадуючи наше визначення обернених функцій, функція\(f\) та її зворотна\(f^{−1}\) задовольняють умовам\(f(f^{−1}(y))=y\) для всіх\(y\) у області\(f^{−1}\) і\(f^{−1}(f(x))=x\) для всіх\(x\) в домен\(f\), так що тут сталося? Проблема полягає в тому, що функція зворотного синуса є оберненою функцією обмеженого синуса, визначеної в області\(\left[−\frac{π}{2},\frac{π}{2}\right]\).\(\sin^{−1}\) Тому, бо\(x\) в інтервалі\([−\frac{π}{2},\frac{π}{2}]\), це правда, що\(\sin^{−1}(\sin x)=x\). Однак для значень\(x\) поза цим інтервалом рівняння не\(\sin^{−1}(\sin x)\) тримається, хоча і визначено для всіх дійсних чисел\(x\).
А як щодо\(\sin(\sin^{−1}y)?\) Чи є у цього подібна проблема? Відповідь - ні. Оскільки область of\(\sin^{−1}\) є інтервалом\([−1,1]\), то робимо висновок, що\(\sin\left(\sin^{−1}y\right)=y\) якщо\(−1≤y≤1\) і вираз не визначено для інших значень\(y\). Підводячи підсумок,
\(\sin(\sin^{−1}y)=y\)якщо\(−1≤y≤1\)
і
\(\sin^{−1}(\sin x)=x\)якщо\(−\frac{π}{2}≤x≤\frac{π}{2}.\)
Аналогічно, для функції косинуса,
\(\cos(\cos^{−1}y)=y\)якщо\(−1≤y≤1\)
і
\(\cos^{−1}(\cos x)=x\)якщо\(0≤x≤π.\)
Подібні властивості тримаються і для інших тригонометричних функцій і їх зворотних.
Оцінити кожне з наведених нижче виразів.
- \(\sin^{−1}\left(−\frac{\sqrt{3}}{2}\right)\)
- \(\tan\left(\tan^{−1}\left(−\frac{1}{\sqrt{3}}\right)\right)\)
- \(\cos^{−1}\left(\cos\left(\frac{5π}{4}\right)\right)\)
- \(\sin^{−1}\left(\cos\left(\frac{2π}{3}\right)\right)\)
Рішення
- Оцінка\(\sin^{−1}(−\sqrt{3}/2)\) еквівалентна знаходженню\(θ\) такого кута, що\(\sin θ=−\sqrt{3}/2\) і\(−π/2≤θ≤π/2\). Кут\(θ=−π/3\) задовольняє цим двом умовам. Тому,\(\sin^{−1}(−\sqrt{3}/2)=−π/3\).
- Для початку скористаємося тим, що\(\tan^{−1}(−1/\sqrt{3})=−π/6.\) Тоді\(\tan(-π/6)=−1/\sqrt{3}\). Тому,\(\tan(\tan^{−1}(−1/\sqrt{3}))=−1/\sqrt{3}\).
- Для оцінки\(\cos^{−1}(\cos(5π/4))\) спочатку використовуйте той факт, що\(\cos(5π/4)=−\sqrt{2}/2\). Потім нам потрібно знайти кут\(θ\) такий, що\(\cos(θ)=−\sqrt{2}/2\) і\(0≤θ≤π\). Так як\(3π/4\) задовольняє обидва ці умови, ми маємо\(\cos^{-1}(\cos(5π/4))=\cos^{−1}(−\sqrt{2}/2))=3π/4\).
- Так як\(\cos(2π/3)=−1/2\), нам потрібно оцінювати\(\sin^{−1}(−1/2)\). Тобто нам потрібно знайти кут\(θ\) такий, що\(\sin(θ)=−1/2\) і\(−π/2≤θ≤π/2\). Оскільки\(−π/6\) задовольняє обом цим умовам, можна зробити висновок, що\(\sin^{−1}(\cos(2π/3))=\sin^{−1}(−1/2)=−π/6.\)
У багатьох областях науки, техніки та математики корисно знати максимальне значення, яке функція може отримати, навіть якщо ми не знаємо її точного значення в даний момент. Наприклад, якщо у нас є функція, що описує міцність балки даху, ми хотіли б знати максимальну вагу, яку може підтримувати балка, не порушуючи. Якщо у нас є функція, яка описує швидкість поїзда, ми хотіли б знати його максимальну швидкість, перш ніж він зіскочить з рейок. Безпечна конструкція часто залежить від знання максимальних значень.
Цей проект описує простий приклад функції з максимальним значенням, яке залежить від двох коефіцієнтів рівняння. Ми побачимо, що максимальні значення можуть залежати від декількох факторів, відмінних від незалежної змінної\(x\).
1. Розглянемо графік на малюнку\(\PageIndex{6}\) функції\(y=\sin x+\cos x.\) Опишіть її загальну форму. Це періодично? Звідки ти знаєш?
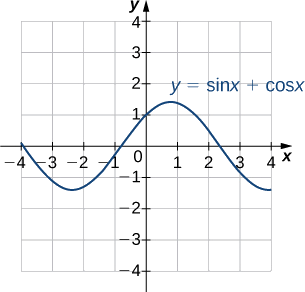
Використовуючи графічний калькулятор або інший графічний пристрій, оцініть\(x\) - і\(y\) -значення максимальної точки для графіка (перша така точка де\(x > 0\)). Може бути корисним висловити\(x\) значення -value як кратне\(π.\)
2. Тепер розглянемо інші графіки виду\(y=A\sin x+B\cos x\) для різних значень\(A\) і\(B.\) Намалюйте графік коли\(A = 2\) і\(B = 1,\) і знайдіть\(x\) - і\(y\) -значення для максимальної точки. (Не забудьте висловити\(x\) -value як кратне\(π\), якщо це можливо.) Він рухався?
3. Повторіть для\(A = 1, \,B = 2.\) Чи є якесь відношення до того, що ви знайшли в частині (2)?
4. Заповніть наступну таблицю, додавши кілька варіантів для\(A\) та\(B:\)
| \(A\) | \(B\) | \(x\) | \(y\) | \(A\) | \(B\) | \(x\) | \(y\) |
|---|---|---|---|---|---|---|---|
| \ (A\)» style="вертикальне вирівнювання: середина; "> 0 | \ (B\)» style="вертикальне вирівнювання: середина; "> 1 | \ (x\)» style="вертикальне вирівнювання: середина; "> | \ (y\)» style="вертикальне вирівнювання: середина; "> | \ (A\)» style="вертикальне вирівнювання: середина; "> 3 | \ (B\)» style="вертикальне вирівнювання: середина; "> 4 | \ (x\)» style="вертикальне вирівнювання: середина; "> | \ (y\)» style="вертикальне вирівнювання: середина; "> |
| \ (A\)» style="вертикальне вирівнювання: середина; "> 1 | \ (B\)» style="вертикальне вирівнювання: середина; "> 0 | \ (x\)» style="вертикальне вирівнювання: середина; "> | \ (y\)» style="вертикальне вирівнювання: середина; "> | \ (A\)» style="вертикальне вирівнювання: середина; "> 4 | \ (B\)» style="вертикальне вирівнювання: середина; "> 3 | \ (x\)» style="вертикальне вирівнювання: середина; "> | \ (y\)» style="вертикальне вирівнювання: середина; "> |
| \ (A\)» style="вертикальне вирівнювання: середина; "> 1 | \ (B\)» style="вертикальне вирівнювання: середина; "> 1 | \ (x\)» style="вертикальне вирівнювання: середина; "> | \ (y\)» style="вертикальне вирівнювання: середина; "> | \ (A\)» style="вертикальне вирівнювання: середина; ">\(\sqrt{3}\) | \ (B\)» style="вертикальне вирівнювання: середина; "> 1 | \ (x\)» style="вертикальне вирівнювання: середина; "> | \ (y\)» style="вертикальне вирівнювання: середина; "> |
| \ (A\)» style="вертикальне вирівнювання: середина; "> 1 | \ (B\)» style="вертикальне вирівнювання: середина; "> 2 | \ (x\)» style="вертикальне вирівнювання: середина; "> | \ (y\)» style="вертикальне вирівнювання: середина; "> | \ (A\)» style="вертикальне вирівнювання: середина; "> 1 | \ (B\)» style="вертикальне вирівнювання: середина; ">\(\sqrt{3}\) | \ (x\)» style="вертикальне вирівнювання: середина; "> | \ (y\)» style="вертикальне вирівнювання: середина; "> |
| \ (A\)» style="вертикальне вирівнювання: середина; "> 2 | \ (B\)» style="вертикальне вирівнювання: середина; "> 1 | \ (x\)» style="вертикальне вирівнювання: середина; "> | \ (y\)» style="вертикальне вирівнювання: середина; "> | \ (A\)» style="вертикальне вирівнювання: середина; "> 12 | \ (B\)» style="вертикальне вирівнювання: середина; "> 5 | \ (x\)» style="вертикальне вирівнювання: середина; "> | \ (y\)» style="вертикальне вирівнювання: середина; "> |
| \ (A\)» style="вертикальне вирівнювання: середина; "> 2 | \ (B\)» style="вертикальне вирівнювання: середина; "> 2 | \ (x\)» style="вертикальне вирівнювання: середина; "> | \ (y\)» style="вертикальне вирівнювання: середина; "> | \ (A\)» style="вертикальне вирівнювання: середина; "> 5 | \ (B\)» style="вертикальне вирівнювання: середина; "> 12 | \ (x\)» style="вертикальне вирівнювання: середина; "> | \ (y\)» style="вертикальне вирівнювання: середина; "> |
5. Спробуйте розібратися з формулою для\(y\) -значень.
6. Формула для\(x\) -значень трохи складніше. Найбільш корисними моментами з таблиці є\((1,1),\, (1,\sqrt{3}),\, (\sqrt{3},1).\) (Підказка: Розглянемо зворотні тригонометричні функції.)
7. Якщо ви знайшли формули для частин (5) і (6), покажіть, що вони працюють разом. Тобто, замініть знайдену формулу\(x\) -value\(y=A\sin x+B\cos x\) і спростіть її, щоб прийти до знайденої вами формули\(y\) -value.
Ключові поняття
- Щоб функція мала зворотну функцію, функція повинна бути один до одного. Враховуючи графік функції, ми можемо визначити, чи є функція один-на-один за допомогою тесту горизонтальної лінії.
- Якщо функція не один до одного, ми можемо обмежити домен меншим доменом, де функція один до одного, а потім визначити зворотну функцію на меншому домені.
- Для функції\(f\) та її зворотного\(f^{−1},\, f(f^{−1}(x))=x\) для всіх\(x\) у області\(f^{−1}\) та\(f^{−1}(f(x))=x\) для всіх\(x\) у області\(f\).
- Оскільки тригонометричні функції є періодичними, нам потрібно обмежити їх області для визначення обернених тригонометричних функцій.
- Графік функції\(f\) та її обернений\(f^{−1}\) симетричні щодо прямої\(y=x.\)
Ключові рівняння
- обернена функція
\(f^{−1}(f(x))=x\)для всіх\(x\)\(D,\) і\(f(f^{−1}(y))=y\) для всіх\(y\) в\(R\).
Глосарій
- тест горизонтальної лінії
- функція\(f\) один до одного тоді і лише тоді, коли кожна горизонтальна лінія перетинає графік\(f\), щонайбільше, одного разу
- обернена функція
- для функції\(f\) обернена функція\(f^{−1}\) задовольняє,\(f^{−1}(y)=x\) якщо\(f(x)=y\)
- обернені тригонометричні функції
- обернення тригонометричних функцій визначено на обмежених доменах, де вони є функціями один до одного
- функція один-на-один
- функція\(f\) один до одного, якщо\(f(x_1)≠f(x_2)\) якщо\(x_1≠x_2\)
- обмежений домен
- підмножина області функції\(f\)
