11.1: Векторно-значні функції

Ми дуже добре знайомі з реальними ціннісними функціями, тобто функціями, виходом яких є дійсне число. У цьому розділі представлені векторно-значні функції - функції, виходом яких є вектор.

Визначення$\PageIndex{1}$: Vector-Valued Functions

Векторно-значна функція - це функція виду

$$\vecs r(t) = \langle\, f(t),g(t)\,\rangle$$

або

$$\vecs r(t) = \langle \,f(t),g(t),h(t)\,\rangle,$$

де$f$,$g$ і$h$ є реальними ціннісними функціями.

Домен$\vecs r$ - це сукупність всіх значень,$t$ для яких$\vecs r(t)$ визначено. Діапазон$\vecs r$ - це набір всіх можливих вихідних векторів$\vecs r(t)$.

Оцінювання та графічне зображення векторно-значних функцій

Оцінювання векторної функції за певним значенням$t$ є простим; просто оцініть кожну компонентну функцію при цьому значенні$t$. Наприклад, якщо$\vecs r(t) = \langle t^2,t^2+t-1\rangle$, то$\vecs r(-2) = \langle 4,1\rangle$. Ми можемо накидати цей вектор, як це робиться на малюнку$\PageIndex{1a}$. Графік багато векторів є громіздким, хоча, тому, як правило, ми не ескіз весь вектор, а тільки кінцева точка. Графік векторно-значної функції - це множина всіх кінцевих точок$\vecs r(t)$, де початкова точка кожного вектора завжди є початковою точкою. На малюнку$\PageIndex{1b}$ ми накидаємо графік$\vecs r$; ми можемо вказати окремі точки на графіку з їх відповідним вектором, як показано на малюнку.

Малюнок$\PageIndex{1}$: Ескіз графіка векторно-значної функції.

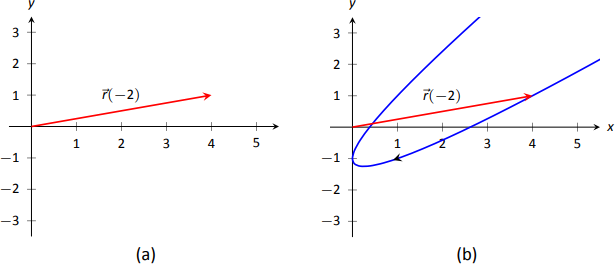
Векторно-значні функції тісно пов'язані з параметричними рівняннями графів. Хоча в обох методах ми будуємо точки$\big(x(t), y(t)\big)$ або$\big(x(t),y(t),z(t)\big)$ створюємо графік, у контексті векторних функцій кожна така точка представляє вектор. Наслідки цього будуть більш повно реалізовані в наступному розділі, оскільки ми застосовуємо ідеї обчислення до цих функцій.

Приклад$\PageIndex{1}$: Graphing vector-valued functions

Графік$\vecs r(t) = \langle t^3-t, \dfrac{1}{t^2+1}\rangle$, для$-2\leq t\leq 2$. Ескіз$\vecs r(-1)$ і$\vecs r(2)$.

Рішення

Почнемо з складання таблиці$x$ і$y$ значень$t$, як показано на малюнку$\PageIndex{1a}$. Побудова цих точок дає вказівку на те, як виглядає графік. На$\PageIndex{1b}$ малюнку вказуємо ці точки і накидаємо повний графік. Також виділяємо$\vecs r(-1)$ і$\vecs r(2)$ на графіку.

Малюнок$\PageIndex{2}$: Ескіз векторної функції Прикладу 11.1.1

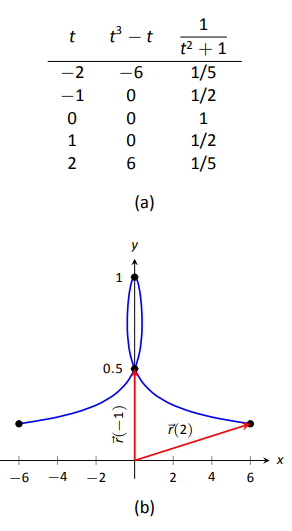
Приклад$\PageIndex{2}$: Graphing vector-valued functions.

Графік$\vecs r(t) = \langle \cos t,\sin t,t\rangle$ для$0\leq t\leq 4\pi$.

Рішення

Ми можемо знову намітити точки, але ретельний розгляд цієї функції дуже показово. Миттєво ігноруючи третій компонент, ми бачимо, що$x$ і$y$ компоненти простежують коло радіуса 1 з центром у початковій точці. Помітивши, що$z$ складова є$t$, ми бачимо, що коли графік накручується навколо$z$ -осі, він також збільшується з постійною швидкістю в позитивному$z$ напрямку, утворюючи спіраль. Це зображено на малюнку$\PageIndex{3}$. На графіку$\vecs r(7\pi/4)\approx (0.707,-0.707,5.498)$ виділено, щоб допомогти нам зрозуміти графік.

Малюнок$\PageIndex{3}$: Перегляд векторної функції та її похідної в одній точці.

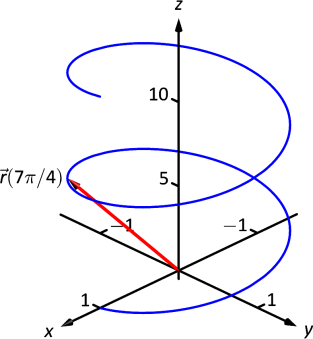
Алгебра векторно-значних функцій

Визначення$\PageIndex{2}$: Operations on Vector-Valued Functions

$\vecs r_1(t)=\langle f_1(t),g_1(t)\rangle$$\vecs r_2(t)=\langle f_2(t),g_2(t)\rangle$Дозволяти і бути векторні функції в$\mathbb{R}^2$ і нехай$c$ бути скалярним. Потім:

1. $\vecs r_1(t) \pm \vecs r_2(t) = \langle\, f_1(t)\pm f_2(t),g_1(t)\pm g_2(t)\,\rangle$.
2. $c\vecs r_1(t) = \langle\, cf_1(t),cg_1(t)\,\rangle$.

Аналогічне визначення має і векторно-значні функції в$\mathbb{R}^3$.

Це визначення стверджує, що ми додаємо, віднімаємо та масштабуємо векторно-значні функції покомпонентно. Поєднання векторно-значних функцій таким способом може бути дуже корисним (а також створювати цікаві графіки).

Приклад$\PageIndex{3}$: Adding and scaling vector-valued functions.

Нехай$\vecs r_1(t) = \langle\,0.2t,0.3t\,\rangle$,$\vecs r_2(t) = \langle\,\cos t,\sin t\,\rangle$ і$\vecs r(t) = \vecs r_1(t)+\vecs r_2(t)$. Графік$\vecs r_1(t)$$\vecs r_2(t)$,$\vecs r(t)$ і$5\vecs r(t)$ далі$-10\leq t\leq10$.

Рішення

Ми можемо графувати$\vecs r_1$ і$\vecs r_2$ легко, будуючи точки (або просто використовуючи технологію). Давайте подумаємо над кожним на мить, щоб краще зрозуміти, як працюють векторні функції.

Ми можемо переписати$\vecs r_1(t) = \langle\, 0.2t,0.3t\,\rangle$ як$\vecs r_1(t) = t\langle 0.2,0.3\rangle$. Тобто функція$\vecs r_1$ масштабує вектор$\langle 0.2,0.3\rangle$ по$t$. Це масштабування вектора створює лінію у напрямку$\langle 0.2,0.3\rangle$.

Ми знайомі з$\vecs r_2(t) = \langle\, \cos t,\sin t\,\rangle$; він простежує коло, по центру в початковій точці, радіусу 1. Малюнок$\PageIndex{4a}$ графіків$\vecs r_1(t)$ і$\vecs r_2(t)$.

Додавання$\vecs r_1(t)$ до$\vecs r_2(t)$ виробляє$\vecs r(t) = \langle\,\cos t + 0.2t,\sin t+0.3t\,\rangle$, графічно показано на малюнку$\PageIndex{4b}$. Лінійний рух лінії поєднується з колом для створення петель, які рухаються в напрямку$\langle 0.2,0.3\rangle$. (Ми закликаємо читача$\vecs r_1(t)$ експериментувати$\langle 2t,3t\rangle$, змінюючи на тощо, і спостерігати за ефектами на петлі.)

Малюнок$\PageIndex{4}$: Графік функцій у прикладі$\PageIndex{3}$

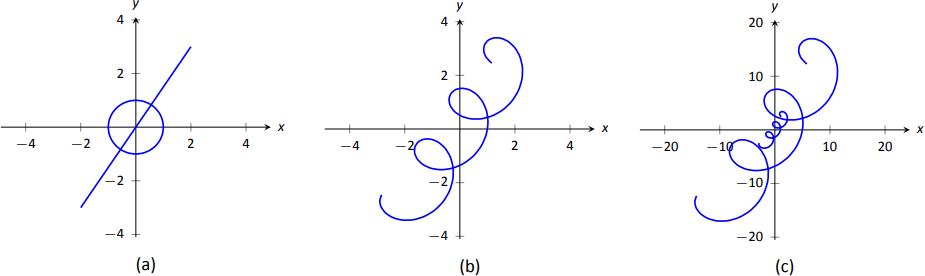
Множення$\vecs r(t)$ на 5 масштабує функцію на 5, виробляючи$5\vecs r(t) = \langle 5\cos t+1,5\sin t+1.5\rangle$, яка зображена на малюнку$\PageIndex{4c}$ разом з$\vecs r(t)$. Нова функція «в 5 разів більше», ніж$\vecs r(t)$. Зверніть увагу, як графік$5\vecs r(t)$ in (c) виглядає ідентичним графіку$\vecs r(t)$ in$(b)$. Це пов'язано з тим, що$x$ і$y$ межі сюжету в рівно в$(c)$ 5 разів більше, ніж межі в (б).

Приклад$\PageIndex{4}$: Adding and scaling vector-valued functions.

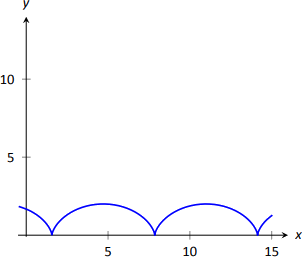
Циклоїда - це графік, промальований точкою$p$ на коченому колі, як показано на малюнку$\PageIndex{5}$. Знайдіть рівняння, що описує циклоїду, де коло має радіус 1.

Малюнок$\PageIndex{5}$: Відстеження циклоїда.

Рішення

Ця проблема не дуже складна, якщо підійти до неї розумно. Почнемо з того, що$\vecs p(t)$ дозволимо описати положення точки$p$ на колі, де коло центрується біля початку і обертається тільки за годинниковою стрілкою (тобто не котиться). Це відносно просто, враховуючи наш попередній досвід роботи з параметричними рівняннями;$\vecs p(t) = \langle \cos t, -\sin t\rangle$.

Тепер ми хочемо, щоб коло згорнувся. Ми представляємо це, дозволяючи$\vecs c(t)$ представляти розташування центру кола. Повинно бути зрозуміло, що$y$ складова$\vecs c(t)$ повинна бути 1; центр кола завжди буде дорівнює 1, якщо він котиться по горизонтальній поверхні.

$x$Компонент$\vecs c(t)$ є лінійною функцією$t$:$f(t) = mt$ для деяких скалярних$m$. Коли$t=0$,$f(t) = 0$ (коло починається з центру на$y$ -осі). Коли$t=2\pi$, коло зробив один повний оборот, пройшовши відстань, рівну його окружності, яка теж є$2\pi$. Це дає нам точку на нашій лінії$f(t) = mt$, точку$(2\pi, 2\pi)$. Повинно бути зрозуміло, що$m=1$ і$f(t) = t$. Отже$\vecs c(t) = \langle t, 1\rangle$.

Тепер об'єднаємо$\vecs p$ і$\vecs c$ разом сформуємо рівняння циклоїди:

$$\vecs r(t) = \vecs p(t) + \vecs c(t) = \langle \cos t+ t,-\sin t+1\rangle, \nonumber$$

який зображений на малюнку$\PageIndex{6}$.

Малюнок$\PageIndex{6}$: Циклоїд у прикладі$\PageIndex{4}$.

Водотоннажність

Векторно-значна функція часто$\vecs r(t)$ використовується для опису положення рухомого об'єкта в часі$t$. В$t=t_0$, об'єкт знаходиться в$\vecs r(t_0)$; в$t=t_1$, об'єкт знаходиться в$\vecs r(t_1)$. Знаючи локації$\vecs r(t_0)$ і$\vecs r(t_1)$ не вказуючи на шлях, пройдений між ними, але часто ми дбаємо лише про різницю локацій$\vecs r(t_1)-\vecs r(t_0)$, зміщення.

Визначення$\PageIndex{3}$: Displacement

$\vecs r(t)$Дозволяти бути векторної функції і нехай$t_0<t_1$ бути значення в області. $\vecs d$Зсув$\vecs r$, від$t=t_0$ до$t=t_1$, є $$\vecs d=\vecs r(t_1)-\vecs r(t_0).$$

Коли вектор зміщення малюється з початковою точкою в$\vecs r(t_0)$, його кінцева точка є$\vecs r(t_1)$. Ми думаємо про це як вектор, який вказує від початкової позиції до кінцевої позиції.

Приклад$\PageIndex{5}$: Finding and graphing displacement vectors

Нехай$\vecs r(t) = \langle \cos (\dfrac{\pi}{2}t),\sin (\dfrac{\pi}2 t)\rangle$. Графік$\vecs r(t)$ далі$-1\leq t\leq 1$, і знайдіть зсув$\vecs r(t)$ на цьому інтервалі.

Рішення

Функція$\vecs r(t)$ простежує одиничне коло, хоча і з іншою швидкістю, ніж «звичайна»$\langle \cos t,\sin t\rangle$ параметризація. На$t_0=-1$, у нас є$\vecs r(t_0) = \langle 0,-1\rangle$; в$t_1=1$, у нас є$\vecs r(t_1) = \langle 0,1\rangle$. Зсув$\vecs r(t)$ на, таким$[-1,1]$ чином,

$$\vecs d = \langle 0,1\rangle - \langle 0,-1\rangle = \langle 0,2\rangle. \nonumber$$

Малюнок$\PageIndex{7}$: Графік зсуву функції позиції у прикладі$\PageIndex{5}$.

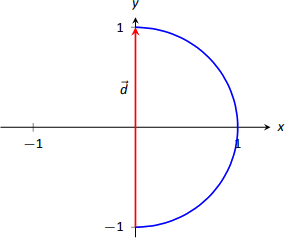
Графік включення$\vecs r(t)$$[-1,1]$ наведено на малюнку$\PageIndex{7}$ разом з вектором зміщення$\vecs d$ на цьому інтервалі.

Вимірювання переміщення змушує нас розглядати пов'язані, але дуже різні поняття. Враховуючи напівкруглий шлях, який$\PageIndex{5}$ взяв об'єкт у прикладі, ми можемо швидко перевірити, що об'єкт закінчився на відстані 2 одиниці від свого початкового розташування. Тобто ми можемо обчислити$\norm{d} = 2$. Однак вимірювання відстані від початкової точки відрізняється від вимірювання пройденої відстані. Будучи півколом, ми можемо виміряти пройдену цим об'єктом відстань як$\pi\approx 3.14$ одиниці. Знання відстані від початкової точки дозволяє обчислити середню швидкість зміни.

Визначення$\PageIndex{4}$: Average Rate of Change

$\vecs r(t)$Дозволяти векторно-значна функція, де кожна з її складових функцій є безперервною на своїй області, і нехай$t_0<t_1$. Середня швидкість зміни$\vecs r(t)$ включення$[t_0,t_1]$ становить

$$\text{average rate of change} = \dfrac{\vecs r(t_1) - \vecs r(t_0)}{t_1-t_0}.$$

Приклад$\PageIndex{6}$: Average rate of change

Нехай$\vecs r(t) = \langle \cos(\dfrac{\pi}2t),\sin(\dfrac{\pi}2t)\rangle$ як у прикладі 11.1.5. Знайти середню швидкість зміни$\vecs r(t)$ включення$[-1,1]$ і включення$[-1,5]$.

Рішення

Ми обчислили в прикладі$\PageIndex{5}$, що зміщення$\vecs r(t)$ на$[-1,1]$ було$\vecs d = \langle 0,2\rangle$. Таким чином, середня швидкість зміни$\vecs r(t)$ на$[-1,1]$ становить:

$$\dfrac{\vecs r(1) -\vecs r(-1)}{1-(-1)} = \dfrac{\langle 0,2\rangle}{2} = \langle 0,1\rangle. \nonumber$$

Ми інтерпретуємо це так: об'єкт йшов напівкруглим шляхом, тобто він рухався вправо, потім перемістився назад вліво, при цьому піднімаючись повільно, потім швидко, потім знову повільно. В середньому, однак, він прогресував прямо вгору з постійною швидкістю$\langle 0,1\rangle$ в одиницю часу.

Ми швидко бачимо, що зміщення на$[-1,5]$ таке ж, як і на$[-1,1]$, так$\vecs d = \langle 0,2\rangle$. Середня швидкість зміни різна, хоча:

$$\dfrac{\vecs r(5)-\vecs r(-1)}{5-(-1)} = \dfrac{\langle 0,2\rangle}{6} = \langle 0,1/3\rangle. \nonumber$$

Оскільки «3 рази більше часу» знадобилося, щоб прибути в одне і те ж місце, ця середня швидкість зміни$1/3$ на$[-1,5]$ є середньою швидкістю зміни на$[-1,1]$.

Ми розглядали середні темпи змін у розділах 1.1 та 2.1, вивчаючи межі та похідні. Те саме і тут; у наступному розділі ми застосовуємо поняття числення до векторних функцій, оскільки знаходимо межі, похідні та інтеграли. Розуміння середньої швидкості змін дасть нам розуміння похідної; переміщення дає нам одне застосування інтеграції.

Автори та атрибуція

• Template:ContribApexCalc