9.4: Вступ до полярних координат

Last updated
Save as PDF

Page ID: 60839

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Ми, як правило, знайомі з ідеєю графічних кривих шляхом відношення$x$ -values до$y$ -values через функцію$f$. Тобто, ми встановлюємо$y=f(x)$, і будуємо багато пар точок,$(x,y)$ щоб отримати гарне уявлення про те, як виглядає крива. Цей метод корисний, але має обмеження, не останнє з яких полягає в тому, що криві, які «провалюють тест вертикальної лінії», не можуть бути побудовані графіками без використання декількох функцій.

Попередні два розділи ввели і вивчали новий спосіб побудови точок у$x,y$ -площині. Використовуючи параметричні рівняння,$x$ і$y$ значення обчислюються незалежно, а потім будуються разом. Цей метод дозволяє нам графікувати надзвичайний діапазон кривих. Цей розділ представляє ще один спосіб побудови точок на площині: використання полярних координат.

Полярні координати

Почніть з точки$O$ в площині, яка називається полюсом (ми завжди будемо ідентифікувати цю точку з початком). Від полюса намалюйте промінь, званий початковим променем (цей промінь ми завжди будемо малювати горизонтально, ототожнюючи його з позитивною$x$ -віссю). Точка$P$ в площині визначається відстанню,$r$ яке$P$ знаходиться від$O$, і кутом,$\theta$ утвореним між початковим променем і відрізком$\overline{OP}$ (вимірюється проти годинникової стрілки). Записуємо відстань і кут як впорядковану пару$(r,\theta)$. Щоб уникнути плутанини з прямокутними координатами, позначимо полярні координати буквою$P$, як в$P(r,\theta)$. Це проілюстровано на рис$\PageIndex{1}$.

9.36.ПНГ — Малюнок$\PageIndex{1}$: Ілюстрація полярних координат.

Практика зробить цей процес більш зрозумілим.

Приклад$\PageIndex{1}$: Plotting Polar Coordinates

Побудуйте наступні полярні координати:

\[A = P(1,\pi/4)\quad B=P(1.5,\pi)\quad C = P(2,-\pi/3)\quad D = P(-1,\pi/4)\]

Рішення

Малюнок$\PageIndex{2}$: Побудова полярних точок у прикладі 9.4.1

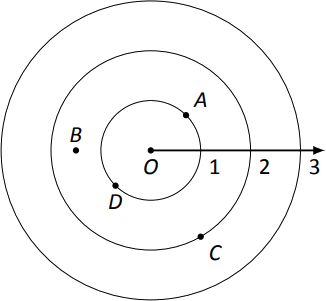
Щоб допомогти у малюванні, внизу цієї сторінки передбачена полярна сітка. Щоб розмістити точку$A$, вийдіть на 1 одиницю вздовж початкового променя (поклавши вас на внутрішнє коло, показане на сітці), потім поверніть$\pi/4$ радіани проти годинникової стрілки (або$45^\circ$). По черзі спочатку можна розглянути обертання: подумайте про промінь$O$, від якого утворюється кут$\pi/4$ з початковим променем, потім висуньте 1 одиницю уздовж цього променя (знову розміщуючи вас на внутрішньому колі сітки).

Для побудови сюжету$B$ вийдіть$1.5$ одиниці вздовж початкового променя і обертайте$\pi$ радіани ($180^\circ$).

Для побудови$C$ графіка вийдіть 2 одиниці вздовж початкового променя, а потім обертайте$\pi/3$ радіани за годинниковою стрілкою, оскільки заданий кут є негативним.

Для побудови сюжету$D$ рухайтеся вздовж початкового променя одиниць — іншими словами, «назад вгору» на 1 одиницю, потім обертайте проти годинникової стрілки на$\pi/4$.$-1$ Результати наведені на рис$\PageIndex{2}$.

Розглянемо наступні два моменти:$A = P(1,\pi)$ і$B = P(-1,0)$. Щоб знайти$A$, вийдіть з 1 одиниці на початковому промені, а потім обертайте$\pi$ радіани; щоб знайти$B$, вийти$-1$ одиниць на початковому промені і не обертати. Слід бачити, що$A$ і$B$ розташовані в одній точці в площині. Ми також можемо розглянути$C=P(1,3\pi)$, або$D = P(1,-\pi)$; всі чотири з цих точок мають одне і те ж місце розташування.

Ця здатність ідентифікувати точку на площині з множинними полярними координатами є одночасно і «благословенням», і «прокляттям». Ми побачимо, що це корисно, оскільки ми можемо побудувати красиві функції, які перетинаються (так само, як ми бачили з параметричними функціями). Нещасливою частиною цього є те, що буває важко визначити, коли це станеться. Ми розглянемо це докладніше пізніше в цьому розділі.

Полярний до прямокутний Перетворення

Корисно розпізнати як прямокутні (або декартові) координати точки на площині, так і її полярні координати. $\PageIndex{3}$На малюнку показана точка$P$ в площині з прямокутними координатами$(x,y)$ і полярними координатами$P(r,\theta)$. Використовуючи тригонометрію, ми можемо зробити ідентичності, наведені в наступній Ключовій ідеї.

9.38 ПНГ — Малюнок$\PageIndex{3}$: Перетворення між прямокутними та полярними координатами.

KEY IDEA 40 Перетворення між прямокутними та полярними координатами

З урахуванням полярної точки$P(r,\theta)$ прямокутні координати визначаються

\[x=r\cos \theta\qquad y=r\sin \theta.\]

З огляду на прямокутні координати$(x,y)$, полярні координати визначаються

\[ r^2=x^2+y^2\qquad \tan \theta = \frac yx.\]

Приклад$\PageIndex{2}$: Converting Between Polar and Rectangular Coordinates

Перетворіть полярні$P(-1,5\pi/4)$ координати$P(2,2\pi/3)$ та прямокутні координати.
Перетворіть прямокутні координати$(1,2)$ та$(-1,1)$ полярні координати.

(а) Починаємо з$P(2,2\pi/3)$. Використовуючи Key Idea 40, ми маємо\[x= 2\cos (2\pi/3) = -1\qquad y = 2\sin (2\pi/3) = \sqrt{3}.\] Так прямокутні координати є$(-1,\sqrt{3}) \approx (-1,1.732)$.

(b) Полярна точка$P(-1,5\pi/4)$ перетворюється на прямокутну за допомогою:\[x=-1\cos (5\pi/4) = \sqrt{2}/2\qquad y= -1\sin (5\pi/4) = \sqrt{2}/2.\]

Отже, прямокутні координати є$(\sqrt{2}/2,\sqrt{2}/2) \approx (0.707,0.707)$.

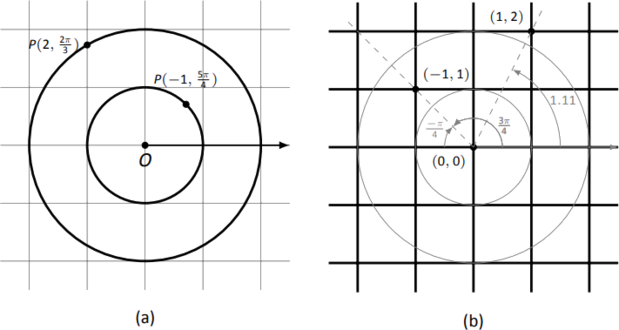
Ці точки побудовані на малюнку$\PageIndex{4}$ (а). Прямокутна система координат намальована злегка під полярною системою координат, щоб можна було побачити зв'язок між ними.
(а) Щоб перетворити прямокутну точку$(1,2)$ в полярні координати, ми використовуємо Ключову ідею для формування наступних двох рівнянь:
\[1^2+2^2 = r^2 \qquad \tan \theta = \frac{2}{1}.\] Перше рівняння говорить нам про це$r=\sqrt{5}$. Використовуючи обернену тангенсну функцію, ми знаходимо\[\tan \theta = 2 \quad \Rightarrow \quad \theta = \tan^{-1} 2 \approx 1.11\approx 63.43^\circ.\] This полярні координати$(1,2)$ є$P(\sqrt{5},1.11)$.

(b) Для перетворення в$(-1,1)$ полярні координати ми формуємо рівняння\[(-1)^2+1^2=r^2 \qquad \tan \theta = \frac{1}{-1}.\]

Таким чином$r=\sqrt{2}$. Ми повинні бути обережними в обчисленні$\theta$: використовуючи обернену функцію дотичної, ми маємо\[\tan\theta = -1 \quad \Rightarrow \quad \theta = \tan^{-1}(-1) = -\pi/4 = -45^\circ.\]

Це не той кут, який ми хочемо. Діапазон$\tan^{-1}x$ є$(-\pi/2,\pi/2)$; тобто повертає кути, які лежать в$1^\text{st}$ і$4^\text{th}$ квадрантах. Щоб знайти місця в$2^\text{nd}$ і$3^\text{rd}$ квадрантах, додайте$\pi$ до результату$\tan^{-1}x$. Так$\pi+(-\pi/4)$ ставить кут на$3\pi/4$. Таким чином, полярна точка є$P(\sqrt{2},3\pi/4)$.

Альтернативним методом є використання кута,$\theta$ заданого арктангенсом, але зміна знака$r$. Таким чином, ми могли б також посилатися$(-1,1)$ як\\$P(-\sqrt{2},-\pi/4)$.

Ці точки нанесені на малюнку$\PageIndex{4}$ (б). Полярна система намальована злегка під прямокутною сіткою з променями, щоб продемонструвати використовувані кути.

Малюнок$\PageIndex{4}$: Побудова прямокутних та полярних точок у прикладі 9.4.2

Полярні функції та полярні графіки

Визначення нової системи координат дозволяє нам створити новий вид функції, полярну функцію. Прямокутні координати добре піддавалися створенню функцій, які пов'язані$y$,$x$ і, наприклад,$y=x^2.$ Полярні координати дозволяють нам створювати функції, які стосуються$r$ і$\theta$. Зазвичай ці функції виглядають$r=f(\theta)$, хоча ми можемо створювати функції форми$\theta = f(r)$. Наступні приклади знайомлять нас з цим поняттям.

Приклад$\PageIndex{3}$: Introduction to Graphing Polar Functions

Опишіть графіки наступних полярних функцій.

$r = 1.5$
$\theta = \pi/4 $

Рішення

Рівняння$r=1.5$ описує всі точки, які знаходяться в 1,5 одиниці від полюса; оскільки кут не заданий,$\theta$ допустимий будь-який. Всі точки 1,5 одиниці від полюса описує коло радіусом 1,5.

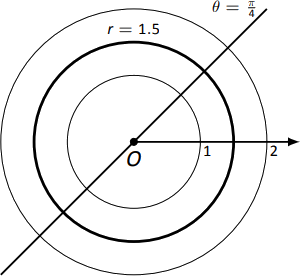
Ми можемо розглянути прямокутний еквівалент цього рівняння; використовуючи$r^2=x^2+y^2$, ми бачимо$1.5^2=x^2+y^2$, що, яке ми визнаємо рівнянням кола з центром$(0,0)$ з радіусом 1.5. Це намальовано на малюнку$\PageIndex{5}$.
Рівняння$\theta = \pi/4$ описує всі точки таким чином, що лінія через них і полюс складають кут$\pi/4$ з початковим променем. Оскільки радіус не$r$ заданий, він може бути будь-яким значенням (навіть негативним). Таким чином$\theta = \pi/4$ описується лінія через полюс, який робить кут$\pi/4 = 45^\circ$ з початковим променем.

Можна знову розглянути прямокутний еквівалент цього рівняння. Об'єднати$\tan \theta =y/x$ і$\theta =\pi/4$:\[\tan \pi/4 = y/x \quad \Rightarrow x\tan \pi/4 = y \quad \Rightarrow y = x.\] Цей графік також побудовано на малюнку$\PageIndex{5}$.

Малюнок$\PageIndex{5}$: Побудова стандартних полярних ділянок.

Основні прямокутні рівняння утворюють$x=h$ і$y=k$ створюють вертикальні і горизонтальні лінії відповідно; основні полярні рівняння$r= h$$\theta =\alpha$ створюють кола і лінії через полюс відповідно. За допомогою цього в якості основи ми можемо створити більш складні полярні функції форми$r=f(\theta)$. Вхід - кут; вихід - довжина, наскільки далеко в напрямку кута вийти.

Ми накидаємо ці функції так само, як накидаємо прямокутні та параметричні функції: ми будуємо багато точок і «з'єднуємо точки» з кривими. Ми демонструємо це в наступному прикладі.

Приклад$\PageIndex{4}$: Sketching Polar Functions

Намалюйте$r=1+\cos \theta$ полярну функцію$[0,2\pi]$, намалювавши точки.

Рішення

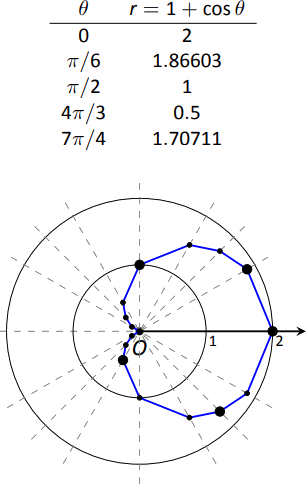
Поширеним питанням під час ескізу кривих шляхом побудови точок є «Які точки слід будувати?» З прямокутними рівняннями ми часто вибираємо «легкі» значення - цілі числа, а потім додаємо більше, якщо потрібно. При побудові полярних рівнянь починайте з «загальних» кутів — кратних$\pi/6$ і$\pi/4$. Рисунок$\PageIndex{6}$ дає таблицю з декількох значень$\theta$ in$[0,\pi]$.

Розглянемо точку,$P(0,2)$ визначену першим рядком таблиці. Кут дорівнює 0 радіанів - ми не обертаємося від початкового променя - тоді ми виходимо 2 одиниці від полюса. Коли$\theta=\pi/6$,$r = 1.866$ (власне, це так$1+\sqrt{3}/2$); так обертаються на$\pi/6$ радіани і виходять 1.866 одиниць.

На показаному графіку використовується більше точок, пов'язаних прямими лініями. (Точки на графіку, які відповідають точкам у таблиці, позначаються більшими крапками.) Такий ескіз, швидше за все, досить хороший, щоб дати уявлення про те, як виглядає графік.

Малюнок$\PageIndex{6}$: Графік полярної функції в прикладі 9.4.4 шляхом побудови точок.

Технологічна примітка

Побудова функцій таким чином може бути стомлюючим, як це було з прямокутними функціями. Для отримання дуже точних графіків технологія є відмінним помічником. Більшість графічних калькуляторів можуть будувати полярні функції; у меню встановіть режим побудови на щось на зразок$\texttt{polar}$ або$\texttt{POL}$, залежно від свого калькулятора. Як і при побудові параметричних функцій, «вікно» перегляду більше не визначає$x$ -значення, які будуються, тому потрібно надати додаткову інформацію. Часто з «віконними» настройками виступають налаштування початкових і кінцевих$\theta$ значень (часто називаються$\theta_{\text{min}}$ і$\theta_{\text{max}}$), а також$\theta_{\text{step}}$ — тобто на те, наскільки далеко один від одного розставлені$\theta$ значення. Чим менше$\theta_{\text{step}}$ значення, тим точніше графік (що також збільшує час побудови графіка). Використовуючи технологію, ми намалювали полярну функцію$r=1+\cos \theta$ з прикладу 9.4.4 на рис$\PageIndex{7}$.

Рисунок$\PageIndex{7}$: Використання технології для графіка полярної функції.

Приклад$\PageIndex{5}$: Sketching Polar Functions

Намалюйте$r=\cos (2\theta)$ полярну функцію$[0,2\pi]$, намалювавши точки.

Рішення

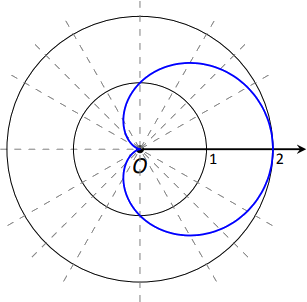
Починаємо з складання таблиці$\cos (2\theta)$ оцінюваних під загальними кутами$\theta$, як показано на малюнку$\PageIndex{8}$. Ці точки потім малюються на малюнку$\PageIndex{9}$ (а). Цей конкретний графік «рухається» навколо зовсім небагато, і можна легко забути, які точки повинні бути пов'язані один з одним. Щоб допомогти нам у цьому, ми пронумерували кожну точку в таблиці і на графіку.

Малюнок$\PageIndex{8}$: Таблиці точок для побудови полярної кривої.

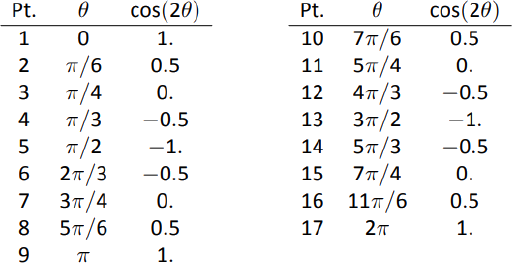
Використовуючи більше точок (і допомогу технології) можна зробити більш плавний графік, як показано на малюнку$\PageIndex{9}$ (b). Ця ділянка є прикладом кривої троянди.

Малюнок$\PageIndex{9}$: Полярні ділянки з прикладу 9.4.5

Іноді бажано посилатися на графік за допомогою полярного рівняння, а в інших випадках - прямокутним рівнянням. Тому необхідно вміти конвертувати між полярними та прямокутними функціями, що ми практикуємо в наступному прикладі. Ми будемо часто використовувати ідентичності, знайдені в Key Idea 40.

Приклад$\PageIndex{6}$: Converting between rectangular and polar equations.

Перетворення з прямокутної в полярну.

$y=x^2$
$xy = 1$

Перетворення від полярного до прямокутного.

$ r=\frac{2}{\sin \theta-\cos\theta}$
$r=2\cos \theta$

Рішення

Замінити на$r\sin\theta$ і$y$$x$ замінити на$r\cos\theta$, даючи:
\[\begin{align*}y &=x^2\\r\sin\theta &= r^2\cos^2\theta\\\frac{\sin\theta}{\cos^2\theta} &= r\end{align*}\]

Ми виявили, що$r=\sin\theta/\cos^2\theta = \tan\theta\sec\theta$. Область цієї полярної функції є$(-\pi/2,\pi/2)$; побудуйте кілька пунктів, щоб побачити, як знайома парабола простежується полярним рівнянням.
Ми знову замінюємо$x$ та$y$ використовуємо стандартні ідентичності та працюємо над вирішенням для$r$:\[\begin{align*}xy &= 1 \\r\cos\theta\cdot r\sin\theta & = 1\\r^2 & = \frac{1}{\cos\theta\sin\theta}\\r & = \frac{1}{\sqrt{\cos\theta\sin\theta}}\\\end{align*}\]

Ця функція дійсна лише тоді, коли добуток$\cos\theta\sin\theta$ позитивний. Це відбувається в першому і третьому квадрантах, тобто область цієї полярної функції є$(0,\pi/2) \cup (\pi,3\pi/2)$.

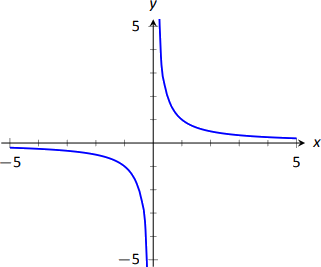
Ми можемо переписати вихідне прямокутне рівняння$xy=1$ як$y=1/x$. Це показано на малюнку$\PageIndex{10}$; зверніть увагу, як він існує лише у першому та третьому квадрантах.
Немає встановленого способу перетворення з полярного на прямокутний; загалом, ми прагнемо сформувати продукти$r\cos \theta$ і$r\sin\theta$, а потім замінити їх на$x$ і$y$, відповідно. Ми починаємо в цій задачі з множення обох сторін на$\sin\theta-\cos\theta$:
\[\begin{align*}r &= \frac{2}{\sin\theta-\cos\theta} \\r(\sin\theta-\cos\theta) &= 2\\r\sin\theta-r\cos\theta &= 2. \qquad \text{Now replace with $y$ and $x$:}\\y-x &= 2\\y &= x+2.\end{align*}\]

Початкове$r=2/(\sin\theta-\cos\theta)$ полярне рівняння, не легко виявити, що його графік є просто лінією. Однак наша конверсія показує, що це так. Майбутня галерея полярних кривих дає загальні рівняння ліній в полярній формі.
Помноживши обидві сторони на$r$, отримуємо і$r^2$ термін, і$r\cos\theta$ термін, який замінюємо на$x^2+y^2$ і$x$ відповідно.
\[\begin{align*}r &=2\cos\theta \\r^2 &= 2r\cos\theta \\x^2+y^2 &= 2x. \end{align*}\]Ми визнаємо це як коло; заповнивши квадрат, ми можемо знайти його радіус і центр.
\[\begin{align}x^2-2x+y^2 &= 0 \$x-1)^2 + y^2 &=1.\end{align}\]

Коло по центру\((1,0)$ і має радіус 1. Майбутня галерея полярних кривих дає рівняння деяких кіл в полярній формі; кола з довільними центрами мають складне полярне рівняння, яке ми тут не розглядаємо.

Малюнок$\PageIndex{10}$: Графік$xy=1$ з прикладу 9.4.6

Деякі криві мають дуже прості полярні рівняння, але досить складні прямокутні. Наприклад, рівняння$r=1+\cos\theta$ описує кардіод (форма, яка важлива, серед іншого, чутливість мікрофонів; один зображений у галереї в розділі Lima\ c con). Прямокутна форма не така проста; це неявне рівняння

\[x^4+y^4+2x^2y^2-2xy^2-2x^3-y^2=0.\]

Перетворення не є «важким», але займає кілька кроків і залишається як проблема в розділі Вправа.

Галерея полярних кривих

Існує ряд основних і «класичних» полярних кривих, що славляться своєю красою та/або застосовністю до наук. Цей розділ закінчується невеликою галереєю деяких з цих графіків. Ми закликаємо читача зрозуміти, як формуються ці графіки, і дослідити за допомогою технології інші типи полярних функцій.

$lines.PNG$

$circles.PNG$

$limacons.PNG$

$rose.PNG$

$special.PNG$

Раніше ми обговорювали, як кожна точка на площині не має унікального уявлення в полярній формі. Це може бути «гарною» річчю, оскільки це дозволяє красиві та цікаві криві, які можна побачити в попередній галереї. Однак це також може бути «поганою» річчю, оскільки буває важко визначити, де перетинаються дві криві.

Приклад$\PageIndex{7}$: Finding points of intersection with polar curves

Визначте, де графи полярних рівнянь$r=1+3\cos\theta$ і$r=\cos \theta$ перетинаються.

Рішення
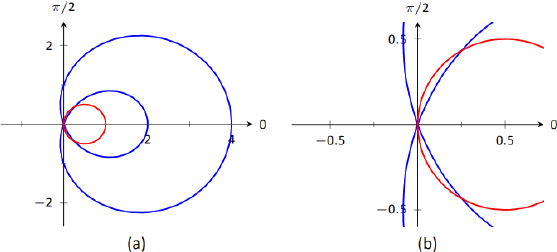
Оскільки технологія, як правило, доступна, як правило, непогано почати з графіка. Ми намалювали дві функції на малюнку$\PageIndex{11}$ (a); щоб краще розрізнити точки перетину, частина (b) фігури збільшується навколо початку.

Рисунок$\PageIndex{11}$: Графіки, які допомагають визначити точки перетину полярних функцій, наведених у прикладі 9.4.7

Почнемо з встановлення двох функцій рівних один одному і рішення для$\theta$:

\ [\ почати {вирівнювати*}
1+3\ cos\ тета &=\ cos\ тета\\
2\ cos\ тета &= -1\\ cos\ theta&= -\ фрак12
\\ тета &=\ фрак {2\ пі} {3},\ frac {4\ pi} {3}.

\ end {вирівнювати*}\]

(Звичайно, існують нескінченні розв'язки рівняння$\cos\theta=-1/2$; оскільки lima\ c con простежується один раз$[0,2\pi]$, ми обмежуємо наші рішення цим інтервалом.)

Потрібно проаналізувати це рішення. Коли$\theta = 2\pi/3$ ми отримаємо точку перетину, яка лежить в$^\text{th}$ квадранті 4. Коли$\theta = 4\pi/3$, ми отримуємо точку перетину, яка лежить в 2$^\text{nd}$ квадранті. Однак про цю другу точку перетину можна сказати більше. Коло, визначене,$r=\cos\theta$ промальовується один раз$[0,\pi]$, це означає, що ця точка перетину виникає під час відстеження кола вдруге. Здається дивним пройти повз точку один раз, а потім розпізнавати її як точку перетину тільки приїхавши туди «вдруге». Перший раз, коли коло прибуває в цей момент, коли$\theta = \pi/3$.

Ключовим є розуміння того, що ці два пункти однакові:$(\cos \pi/3,\pi/3)$ і$(\cos 4\pi/3,4\pi/3)$.

Підсумовуючи те, що ми зробили до цих пір, ми знайшли дві точки перетину: коли$\theta=2\pi/3$ і коли$\theta=4\pi/3$. При посиланні на коло$r=\cos \theta$, остання точка краще посилається, як коли$\theta=\pi/3$.

Є ще одна точка перетину: полюс (або, початок). Ми не розпізнали цю точку перетину, використовуючи нашу роботу вище, оскільки кожен графік приходить до полюса з різним$\theta$ значенням.

Графік перетинає полюс, коли$r=0$. Розглядаючи коло$r=\cos\theta$,$r=0$ коли$\theta = \pi/2$ (і непарні кратні їй, так як коло багаторазово простежується). Ліма\ c con перетинає полюс, коли$1+3\cos\theta =0$; це відбувається коли$\cos \theta = -1/3$, або для$\theta = \cos^{-1}(-1/3)$. Це нестандартний кут, приблизно$\theta = 1.9106 = 10\(\PageIndex{12}$ ^\ circ\). Ліма\ c con двічі перетинає полюс$[0,2\pi]$; інший кут, під яким lima\ c con знаходиться біля полюса, є відображенням першого кута поперек$x$ -осі. Тобто,$\theta = 4.3726 = 250.53^\circ.$

Якщо все одне стосується$(x,y)$ координат, за якими графи перетинаються, значна частина вищевказаної роботи є сторонньою. Ми знаємо, що вони перетинаються$(0,0)$; ми можемо не хвилювати, яка$\theta$ цінність. Аналогічним чином, використовуючи$\theta =2\pi/3$ і$\theta=4\pi/3$ може дати нам необхідні прямокутні координати. Однак у наступному розділі ми застосовуємо поняття числення до полярних функцій. При обчисленні площі області, обмеженої полярними кривими, розуміння нюансів точок перетину стає важливим.

Дописувачі та авторства

Template:ContribApexCalc