10.3: Полярні координати
- Page ID
- 59338
- Графік точок за допомогою полярних координат.
- Перетворення з полярних координат на прямокутні координати.
- Перетворення з прямокутних координат на полярні координати.
- Перетворення рівнянь між полярними і прямокутними формами.
- Визначте і графік полярних рівнянь шляхом перетворення в прямокутні рівняння
За\(12\) кілометри від порту вітрильник стикається з бурхливою погодою і здувається з курсу\(16\) -вузол вітру (див. Рис.\(\PageIndex{1}\)). Яким чином моряк може вказати своє місцезнаходження в Береговій охороні? У цьому розділі ми дослідимо метод представлення місця розташування, який відрізняється від стандартної координатної сітки.
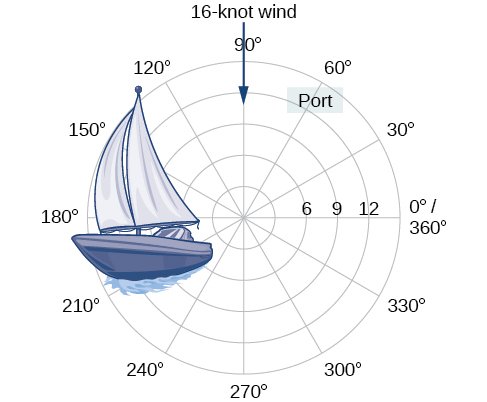
Малюнок\(\PageIndex{1}\)
Побудова точок за допомогою полярних координат
Коли ми думаємо про побудові точок на площині, ми зазвичай думаємо про прямокутні координати\((x,y)\) в декартовій координатній площині. Однак існують і інші способи написання координатної пари та інших типів систем сітки. У цьому розділі ми познайомимо з полярними координатами, які є точками, позначеними\((r,\theta)\) та нанесеними на полярну сітку. Полярна сітка представлена у вигляді ряду концентричних кіл, що випромінюються від полюса, або походження координатної площини.
Полярна сітка масштабується як одиничне коло з позитивною\(x\) - віссю тепер розглядається як полярна вісь, а початок - як полюс. Перша координата\(r\) - радіус або довжина спрямованого відрізка лінії від полюса. Кут\(\theta\), виміряний в радіанах, вказує напрямок\(r\). Рухаємося проти годинникової стрілки від полярної осі на кут\(\theta\), і вимірюємо спрямований відрізок лінії довжиною\(r\) в напрямку\(\theta\). Незважаючи на те, що ми вимірюємо\(\theta\) спочатку\(r\), а потім, полярна точка записується з\(r\) -координатою спочатку. Наприклад, щоб побудувати точку\(\left(2,\dfrac{\pi}{4}\right)\), ми б переміщати\(\dfrac{\pi}{4}\) одиниці в напрямку проти годинникової стрілки, а потім на довжину\(2\) від полюса. Ця точка нанесено на сітку на малюнку\(\PageIndex{2}\).
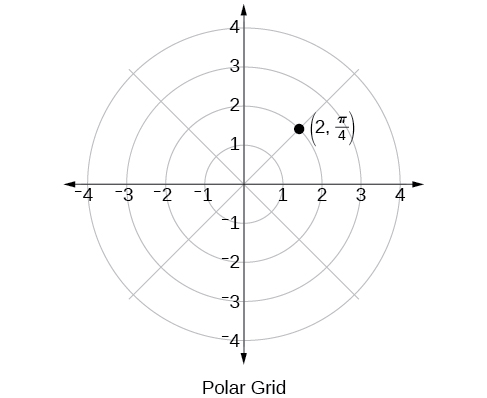
Малюнок\(\PageIndex{2}\)
Покладемо точку\(\left(3,\dfrac{\pi}{2}\right)\) на полярній сітці.
Рішення
\(\dfrac{\pi}{2}\)Кут знаходять шляхом підмітання в напрямку проти годинникової стрілки\(90°\) від полярної осі. Точка розташована на довжині\(3\) одиниць від полюса в\(\dfrac{\pi}{2}\) напрямку, як показано на малюнку\(\PageIndex{3}\).
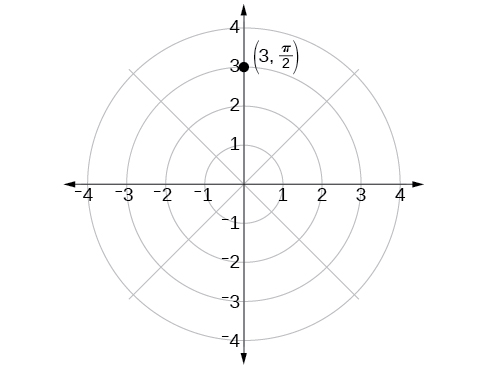
Малюнок\(\PageIndex{3}\)
Побудуйте точку\(\left(2, \dfrac{\pi}{3}\right)\) в полярній сітці.
- Відповідь
-
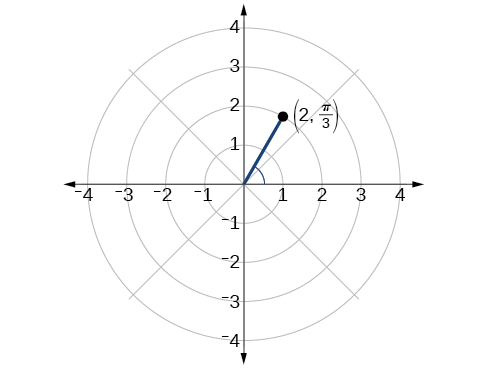
Малюнок\(\PageIndex{4}\)
Покладемо точку\(\left(−2, \dfrac{\pi}{6}\right)\) на полярній сітці.
Рішення
Ми знаємо, що\(\dfrac{\pi}{6}\) знаходиться в першому квадранті. Однак,\(r=−2\). Ми можемо підійти до побудови точки з\(r\) негативом двома способами:
- Покладіть точку,\(\left(2,\dfrac{\pi}{6}\right)\) рухаючись\(\dfrac{\pi}{6}\) у напрямку проти годинникової стрілки та продовжуючи\(2\) одиниці відрізка спрямованої лінії в перший квадрант. Потім відведіть спрямований відрізок лінії назад через полюс, і продовжуйте\(2\) одиниці в третій квадрант;
- Рухайтеся\(\dfrac{\pi}{6}\) в напрямку проти годинникової стрілки і проведіть відрізок спрямованої лінії від\(2\) полюсних одиниць в негативному напрямку, в третій квадрант.
Див\(\PageIndex{5a}\). Малюнок. Порівняйте це з графіком полярної координати,\((2,π6)\) показаним на малюнку\(\PageIndex{5b}\).
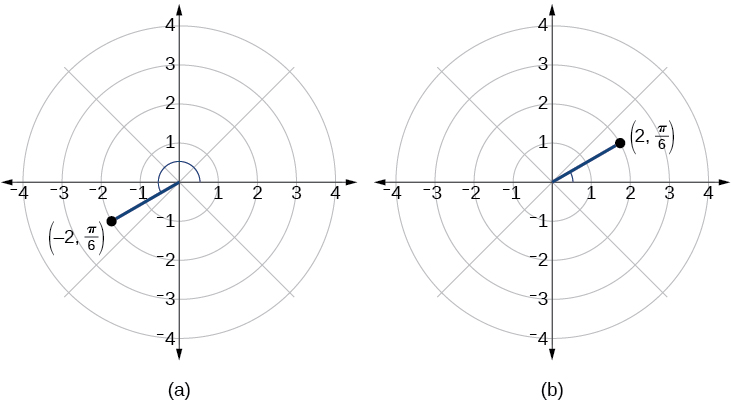
Малюнок\(\PageIndex{5}\)
Покладіть точки\(\left(3,−\dfrac{\pi}{6}\right)\) і\(\left(2,\dfrac{9\pi}{4}\right)\) на тій же полярній сітці.
- Відповідь
-
.jpg)
Малюнок\(\PageIndex{6}\)
Перетворення з полярних координат на прямокутні координати
Якщо задано набір полярних координат, нам може знадобитися перетворити їх у прямокутні координати. Для цього ми можемо згадати відносини, які існують між змінними\(x\),\(y\),\(r\), і\(\theta\).
\(\cos \theta=\dfrac{x}{r}\rightarrow x=r \cos \theta\)
\(\sin \theta=\dfrac{y}{r}\rightarrow y=r \sin \theta\)
Відкидання перпендикуляра від точки в площині до осі х утворює прямокутний трикутник, як показано на малюнку\(\PageIndex{7}\). Простий спосіб запам'ятати рівняння вище - думати про\(\cos \theta\) сусідній стороні над гіпотенузою і\(\sin \theta\) як протилежну сторону над гіпотенузою.
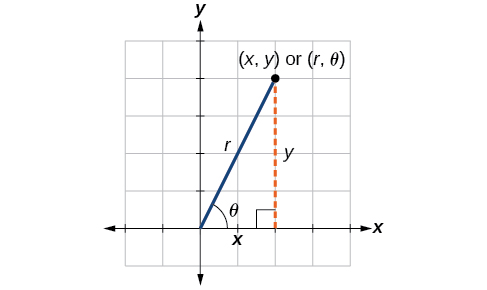
Малюнок\(\PageIndex{7}\)
Щоб перетворити полярні координати\((r, \theta)\) в прямокутні координати\((x, y)\), нехай
\[\cos \theta=\dfrac{x}{r}\rightarrow x=r \cos \theta\]
\[\sin \theta=\dfrac{y}{r}\rightarrow y=r \sin \theta\]
- З огляду на полярну координату\((r,\theta)\), запишіть\(x=r \cos \theta\) і\(y=r \sin \theta\).
- Оцініть\(\cos \theta\) і\(\sin \theta\).
- \(\cos \theta\)Помножте на,\(r\) щоб знайти\(x\) - координату прямокутної форми.
- \(\sin \theta\)Помножте на,\(r\) щоб знайти\(y\) - координату прямокутної форми.
Запишіть полярні координати\(\left(3,\dfrac{\pi}{2}\right)\) як прямокутні координати.
Рішення
Використовуйте еквівалентні відносини.
\[\begin{align*} x&= r \cos \theta\\ x&= 3 \cos \dfrac{\pi}{2}\\ &= 0\\ y&= r \sin \theta\\ y&= 3 \sin \dfrac{\pi}{2}\\ &= 3 \end{align*}\]
Прямокутні координати є\((0,3)\). Див\(\PageIndex{8}\). Малюнок.
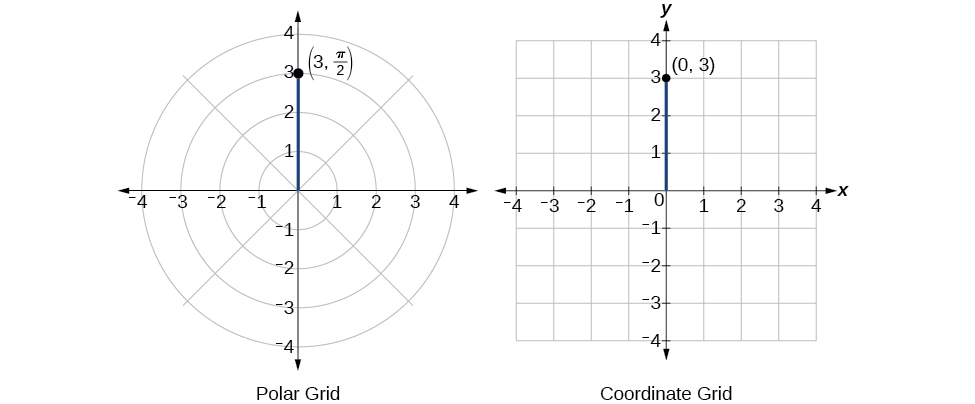
Малюнок\(\PageIndex{8}\)
Запишіть полярні координати\((−2,0)\) як прямокутні координати.
Рішення
Див\(\PageIndex{9}\). Малюнок. Записуючи полярні координати як прямокутні, ми маємо
\[\begin{align*} x&= r \cos \theta\\ x&= -2 \cos(0)\\ &= -2\\ y&= r \sin \theta\\ y&= -2 \sin(0)\\ &= 0 \end{align*}\]
Прямокутні координати також є\((−2,0)\).
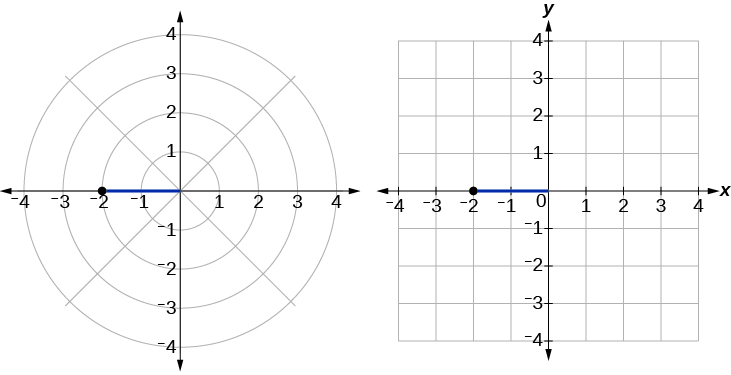
Малюнок\(\PageIndex{9}\)
Запишіть полярні координати\(\left(−1,\dfrac{2\pi}{3}\right)\) як прямокутні координати.
- Відповідь
-
\((x,y)=\left(\dfrac{1}{2},−\dfrac{\sqrt{3}}{2}\right)\)
Перетворення з прямокутних координат на полярні координати
Щоб перетворити прямокутні координати в полярні координати, ми будемо використовувати два інших звичних відносини. Однак при цьому перетворенні нам потрібно знати, що набір прямокутних координат дасть більше однієї полярної точки.
Перетворення прямокутних координат в полярні координати вимагає використання одного або декількох співвідношень, проілюстрованих на малюнку\(\PageIndex{10}\).
\(\cos \theta=\dfrac{x}{r}\)або\(x=r \cos \theta\)
\(\sin \theta=\dfrac{y}{r}\)або\(y=r \sin \theta\)
\(r^2=x^2+y^2\)
\(\tan \theta=\dfrac{y}{x}\)
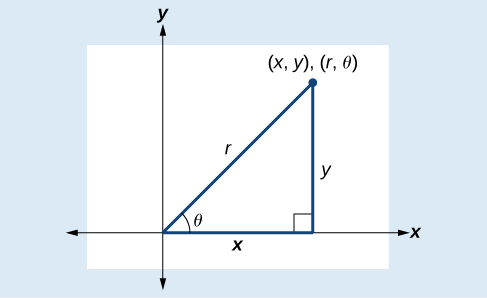
Малюнок\(\PageIndex{10}\)
Перетворіть прямокутні координати\((3,3)\) на полярні координати.
Рішення
Ми бачимо, що початкова точка\((3,3)\) знаходиться в першому квадранті. Щоб знайти\(\theta\), скористайтеся формулою\(\tan \theta=\dfrac{y}{x}\). Це дає
\[\begin{align*} \tan \theta&= \dfrac{3}{3}\\ \tan \theta&= 1\\ {\tan}^{-1}(1)&= \dfrac{\pi}{4} \end{align*}\]
Щоб знайти\(r\), підставляємо значення для\(x\) і\(y\) в формулу\(r=\sqrt{x^2+y^2}\). Ми знаємо, що\(r\) має бути позитивним, як\(\dfrac{\pi}{4}\) і в першому квадранті. Таким чином
\[\begin{align*} r&= \sqrt{3^2+3^2}\\ r&= \sqrt{9+9}\\ r&= \sqrt{18}\\ &= 3\sqrt{2} \end{align*}\]
Отже,\(r=3\sqrt{2}\) і\(\theta=\dfrac{\pi}{4}\), даючи нам полярну точку\((3\sqrt{2},\dfrac{\pi}{4})\). Див\(\PageIndex{11}\). Малюнок.
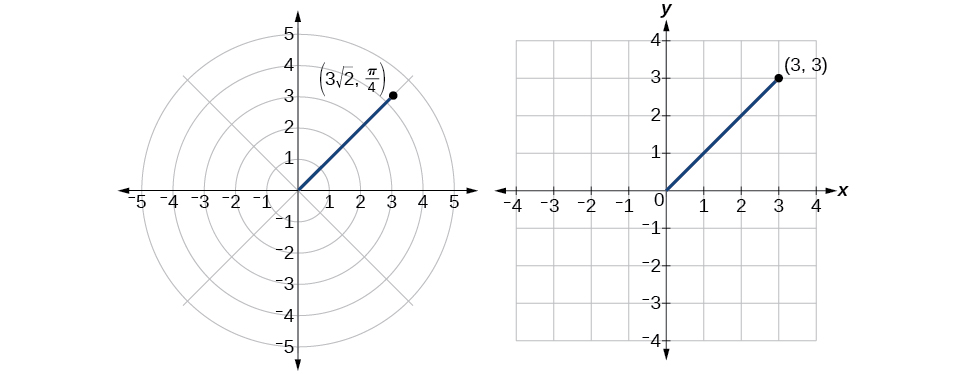
Малюнок\(\PageIndex{11}\)
Аналіз
Є й інші набори полярних координат, які будуть такими ж, як і наше перше рішення. Наприклад, точки\(\left(−3\sqrt{2}, \dfrac{5\pi}{4}\right)\) і\(\left(3\sqrt{2},−\dfrac{7\pi}{4}\right)\) будуть збігатися з вихідним рішенням\(\left(3\sqrt{2}, \dfrac{\pi}{4}\right)\). Точка\(\left(−3\sqrt{2}, \dfrac{5\pi}{4}\right)\) вказує на рух далі проти годинникової стрілки по\(\pi\), який знаходиться прямо навпроти\(\dfrac{\pi}{4}\). Радіус виражається як\(−3\sqrt{2}\). Однак кут\(\dfrac{5\pi}{4}\) розташований в третьому квадранті і, як і\(r\) негативний, ми продовжуємо спрямований відрізок лінії в зворотному напрямку, в перший квадрант. Це той же момент, що і\(\left(3\sqrt{2}, \dfrac{\pi}{4}\right)\). Точка\(\left(3\sqrt{2}, −\dfrac{7\pi}{4}\right)\) - рух далі за годинниковою стрілкою\(−\dfrac{7\pi}{4}\), від\(\dfrac{\pi}{4}\). Радіус\(3\sqrt{2}\),, однаковий.
Перетворення рівнянь між полярними та прямокутними формами
Тепер ми можемо конвертувати координати між полярною та прямокутною формою. Перетворення рівнянь може бути складнішим, але може бути корисним мати можливість конвертувати між двома формами. Оскільки існує ряд полярних рівнянь, які не можуть бути чітко виражені в декартовій формі, і навпаки, ми можемо використовувати ті самі процедури, які ми використовували для перетворення точок між системами координат. Потім ми можемо використовувати графічний калькулятор для графіка або прямокутної форми або полярної форми рівняння.
- Змініть MODE на POL, що представляє полярну форму.
- Натисніть кнопку Y =, щоб викликати екран, що дозволяє вводити шість рівнянь:\(r_1\),\(r_2\),...,\(r_6\).
- Введіть полярне рівняння, встановіть рівне\(r\).
- Натисніть ГРАФ.
Запишіть декартове рівняння\(x^2+y^2=9\) в полярній формі.
Рішення
Мета полягає в тому, щоб виключити\(x\) і\(y\) з рівняння і ввести\(r\) і\(\theta\). В ідеалі, ми б написали рівняння\(r\) як функцію\(\theta\). Для отримання полярної форми ми будемо використовувати відносини між\((x,y)\) і\((r,\theta)\). Так як\(x=r \cos \theta\) і\(y=r \sin \theta\), ми можемо замінити і вирішити для\(r\).
\(\begin{align*} {(r \cos \theta)}^2+{(r \sin \theta)}^2&= 9\\ r^2 {\cos}^2 \theta+r^2 {\sin}^2 \theta&= 9\\ r^2({\cos}^2 \theta+{\sin}^2 \theta)&= 9\\ r^2(1)&= 9\qquad \text {Substitute } {\cos}^2 \theta+{\sin}^2 \theta=1\\ r&= \pm 3\qquad \text {Use the square root property.} \end{align*}\)
Таким чином\(x^2+y^2=9\),\(r=3\), і\(r=−3\) повинен генерувати однаковий графік. Див\(\PageIndex{12}\). Малюнок.
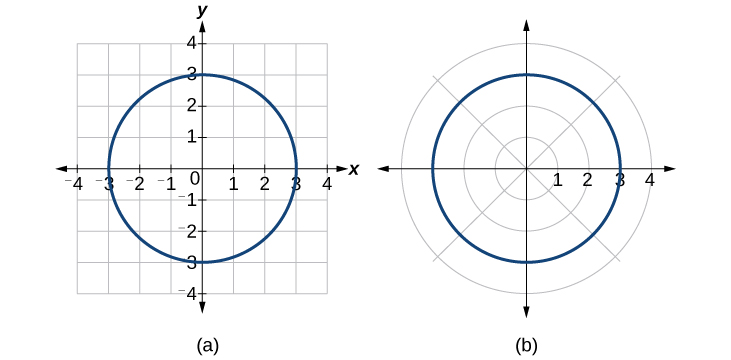
Малюнок\(\PageIndex{12}\): (а) Декартова форма\(x^2+y^2=9\) (б) Полярна форма\(r=3\)
Щоб скласти графік кола в прямокутній формі, ми повинні спочатку вирішити для\(y\).
\[\begin{align*} x^2+y^2&= 9\\ y^2&= 9-x^2\\ y&= \pm \sqrt{9-x^2} \end{align*}\]
Зауважте, що це дві окремі функції, оскільки коло не вдається перевірити вертикальну лінію. Тому нам потрібно ввести позитивні і негативні квадратні корені в калькулятор окремо, як два рівняння у вигляді\(Y_1=\sqrt{9−x^2}\) і\(Y_2=−\sqrt{9−x^2}\). Натисніть ГРАФ.
Перепишіть декартове рівняння\(x^2+y^2=6y\) як полярне рівняння.
Рішення
Це рівняння схоже на попередній приклад, але для перетворення рівняння потрібні різні кроки.
Ми все ще можемо дотримуватися тих самих процедур, які ми вже вивчили, і зробити такі заміни:
\(\begin{array}{ll} r^2=6y & \text{Use }x^2+y^2=r^2. \\ r^2=6r \sin \theta & \text{Substitute }y=r \sin \theta. \\ r^2−6r \sin \theta=0 & \text{Set equal to }0. \\ r(r−6 \sin \theta)=0 & \text{Factor and solve.} \\ r=0 & \text{We reject }r=0 \text{, as it only represents one point, }(0,0). \\ \text{or }r=6 \sin \theta \end{array}\)
Тому рівняння\(x^2+y^2=6y\) і\(r=6 \sin \theta\) повинні дати нам однаковий графік. Див\(\PageIndex{13}\). Малюнок.
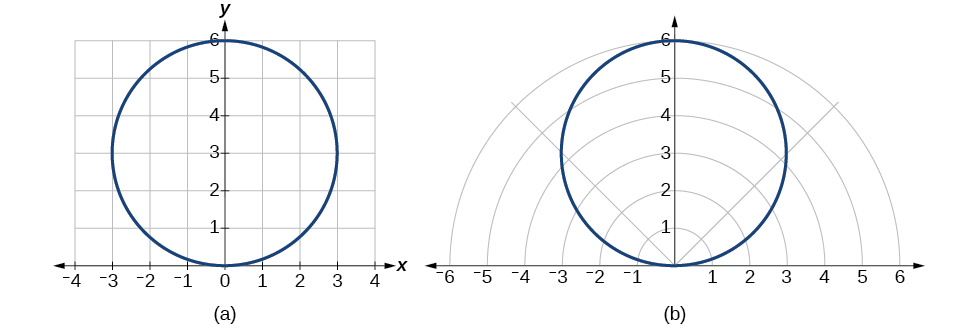
Малюнок\(\PageIndex{13}\): (а) декартова форма\(x^2+y^2=6y\) (б) полярна форма\(r=6 \sin \theta\)
Декартове або прямокутне рівняння наноситься на прямокутну сітку, а полярне рівняння наноситься на полярну сітку. Зрозуміло, що графіки ідентичні.
Переписування декартового рівняння в полярній формі
Перепишіть декартове рівняння\(y=3x+2\) як полярне рівняння.
- Відповідь
-
Ми будемо використовувати відносини\(x=r \cos \theta\) і\(y=r \sin \theta\).
\(\begin{array}{cl} y=3x+2 \\ r \sin \theta=3r \cos \theta+2 \\ r \sin \theta−3r \cos \theta=2 \\ r(\sin \theta−3 \cos \theta)=2 & \text{Isolate }r. \\ r=2 \sin \theta−3\cos \theta & \text{Solve for }r. \end{array}\)
Перепишіть декартове рівняння\(y^2=3−x^2\) в полярній формі.
- Відповідь
-
\(r=\sqrt{3}\)
Визначення та графік полярних рівнянь шляхом перетворення на прямокутні рівняння
Ми навчилися перетворювати прямокутні координати в полярні координати, і ми побачили, що точки дійсно однакові. Ми також перетворили полярні рівняння в прямокутні рівняння і навпаки. Зараз ми продемонструємо, що їх графіки, при цьому намальовані на різних сітках, ідентичні.
Перекрийте полярне рівняння\(r=2 \sec \theta\) в прямокутне рівняння і намалюйте відповідний йому графік.
Рішення
Конверсія є
\[\begin{align*} r &=2 \sec \theta \\ r &= \dfrac{2}{\cos \theta} \\ r \cos \theta &=2 \\ x &=2 \end{align*}\]
Зверніть увагу, що рівняння,\(r=2 \sec \theta\) намальоване на полярній сітці, явно збігається з вертикальною лінією,\(x=2\) накресленою на прямокутній сітці (див. Рис.\(\PageIndex{14}\)). Так само, як\(x=c\) і стандартна форма для вертикальної лінії в прямокутній формі,\(r=c \sec \theta\) є стандартною формою для вертикальної лінії в полярній формі.
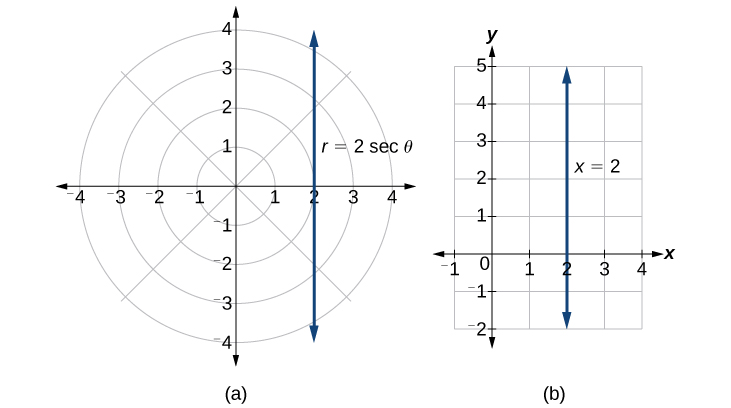
Рисунок\(\PageIndex{14}\): (a) Полярна сітка (b) Прямокутна система координат
Подібне обговорення продемонструвало б, що графіком функції\(r=2 \csc \theta\) буде горизонтальна лінія\(y=2\). По суті,\(r=c \csc \theta\) це стандартна форма для горизонтальної лінії в полярному вигляді, відповідна прямокутної формі\(y=c\).
Перепишіть полярне рівняння\(r=\dfrac{3}{1−2 \cos \theta}\) як декартове рівняння.
Рішення
Мета полягає в тому, щоб усунути\(\theta\) і\(r\), і ввести\(x\) і\(y\). Очищаємо дріб, а потім використовуємо підстановку. Для того, щоб\(r\) замінити на\(x\) and\(y\), ми повинні використовувати вираз\(x^2+y^2=r^2\).
\(\begin{array} r =\dfrac{3}{1−2 \cos \theta} \\ r(1−2 \cos \theta)=3 \\ r\left(1−2\left(\dfrac{x}{r}\right)\right)=3 & \text{Use }\cos \theta=\dfrac{x}{r} \text{ to eliminate }\theta. \\ r−2x=3 \\ r=3+2x & \text{Isolate }r. \\ r^2={(3+2x)}^2 & \text{Square both sides.} \\ x^2+y^2={(3+2x)}^2 & \text{Use }x^2+y^2=r^2. \end{array}\)
Декартове рівняння є\(x^2+y^2={(3+2x)}^2\). Однак, щоб графікувати його, особливо за допомогою графічного калькулятора або комп'ютерної програми, ми хочемо ізолювати\(y\).
\[\begin{align*} x^2+y^2 &= {(3+2x)}^2 \\ y^2 &= {(3+2x)}^2-x^2 \\ y &= \pm {(3+2x)}^2-x^2 \end{align*}\]
Коли все наше рівняння було змінено від\(r\) і\(\theta\) до\(x\) і\(y\), ми можемо зупинитися, якщо не попросять вирішити\(y\) або спростити. Див\(\PageIndex{15}\). Малюнок.
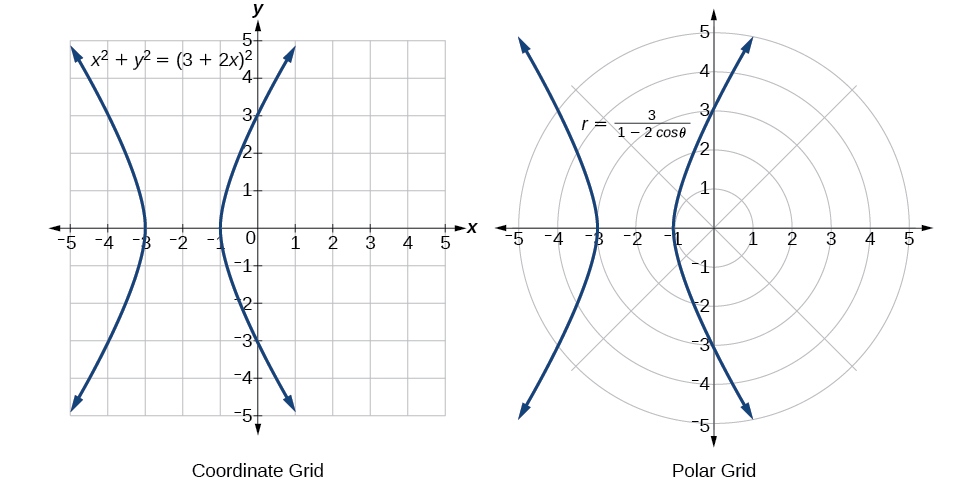
Малюнок\(\PageIndex{15}\)
Форма графіка «пісочний годинник» називається гіперболою. Гіперболи мають багато цікавих геометричних особливостей та застосувань, які ми будемо досліджувати далі в аналітичній геометрії.
Аналіз
У цьому прикладі праву частину рівняння можна розширити, а рівняння спростити далі, як показано вище. Однак рівняння не можна записати як єдину функцію в декартовій формі. Ми можемо записати прямокутне рівняння в стандартній формі гіперболи. Для цього ми можемо почати з початкового рівняння.
\(\begin{array}{ll} x^2+y^2={(3+2x)}^2 \\ x^2+y^2−{(3+2x)}^2=0 \\ x^2+y^2−(9+12x+4x^2)=0 \\ x^2+y^2−9−12x−4x^2=0 \\ −3x^2−12x+y^2=9 & \text{Multiply through by }−1. \\ 3x^2+12x−y^2=−9 \\ 3(x^2+4x)−y2=−9 & \text{Organize terms to complete the square for }x. \\ 3(x^2+4x+4)−y^2=−9+12 \\ 3{(x+2)}^2−y^2=3 \\ {(x+2)}^2−\dfrac{y^2}{3}=1\end{array}\)
Перепишіть полярне рівняння\(r=2 \sin \theta\) в декартовій формі.
- Відповідь
-
\(x^2+y^2=2y\)або, в стандартній формі для кола,\(x^2+{(y−1)}^2=1\)
Перепишіть полярне рівняння\(r=\sin(2\theta)\) в декартовій формі.
Рішення
\(\begin{array}{cl} r=\sin(2\theta) & \text{Use the double angle identity for sine.} \\ r=2 \sin \theta \cos \theta & \text{Use }\cos \theta=\dfrac{x}{r} \text{ and } \sin \theta=\dfrac{y}{r}. \\ r=2 \dfrac{x}{r})(\dfrac{y}{r}) & \text{ Simplify.} \\ r=\dfrac{2xy}{r^2} & \text{Multiply both sides by }r^2. \\ r^3=2xy \\ {(x^2+y^2)}^3=2xy & \text{As }x^2+y^2=r^2, r=\sqrt{x^2+y^2}. \end{array}\)
Це рівняння також можна записати як
\({(x^2+y^2)}^{\frac{3}{2}}=2xy \text{ or }x^2+y^2={(2xy)}^{\frac{2}{3}}\)
Отримайте доступ до цих онлайн-ресурсів для додаткових інструкцій та практики з полярними координатами.
Ключові рівняння
| Формули перетворення |
\(\cos \theta=\dfrac{x}{r} \rightarrow x=r \cos\theta\) \(\sin \theta=\dfrac{y}{r} \rightarrow y=r \sin \theta\) \(r^2=x^2+y^2\) \(\tan \theta=\dfrac{y}{x}\) |
Ключові концепції
- Полярна сітка представлена у вигляді ряду концентричних кіл, що випромінюються з полюса, або походження.
- Для побудови точки в формі\((r,\theta)\)\(\theta>0\), рухатися в напрямку проти годинникової стрілки від полярної осі на кут\(\theta\), а потім продовжити спрямований відрізок лінії від полюса довжиною\(r\) в напрямку\(\theta\). Якщо\(\theta\) негативний, рухатися за годинниковою стрілкою і продовжити спрямований відрізок лінії на довжину\(r\) в напрямку\(\theta\). Див\(\PageIndex{1}\). Приклад.
- Якщо\(r\) негативний, продовжити спрямований відрізок лінії в протилежному напрямку\(\theta\). Див\(\PageIndex{2}\). Приклад.
- Для перетворення з полярних координат в прямокутні, використовуйте формули\(x=r \cos \theta\) і\(y=r \sin \theta\). Див. Приклад\(\PageIndex{3}\) і Приклад\(\PageIndex{4}\).
- Для перетворення прямокутних координат в полярні координати використовуйте одну або декілька формул:\(\cos \theta=\dfrac{x}{r}\)\(\sin \theta=\dfrac{y}{r}\),\(\tan \theta=\dfrac{y}{x}\), і\(r=\sqrt{x^2+y^2}\). Див\(\PageIndex{5}\). Приклад.
- Трансформація рівнянь між полярними і прямокутними формами означає внесення відповідних замін на основі наявних формул разом з алгебраїчними маніпуляціями. Див. розділ Приклад\(\PageIndex{6}\)\(\PageIndex{7}\), Приклад та Приклад\(\PageIndex{8}\).
- Використання відповідних замін дає можливість переписати полярне рівняння як прямокутне рівняння, а потім скласти графік його в прямокутній площині. Див. розділ Приклад\(\PageIndex{9}\)\(\PageIndex{10}\), Приклад та Приклад\(\PageIndex{11}\).
