8.3: Інтегральні та порівняльні тести

Знати, чи збігається серія, дуже важливо, особливо коли ми обговорюємо Power Series. Теореми 60 і 61 дають критерії, коли геометричний і\(p\) -ряд сходяться, а теорема 63 дає швидкий тест, щоб визначити, чи розходиться ряд. Існує багато важливих серій, збіжність яких не може бути визначена цими теоремами, тому ми вводимо набір тестів, які дозволяють нам обробляти широкий спектр рядів. Ми починаємо з інтегрального тесту.

Інтегральний тест

Ми заявили в розділі 8.1, що послідовність\(\{a_n\}\) - це функція, область\(a(n)\) якої є\(\mathbb{N}\), набір натуральних чисел. Якщо ми можемо\(a(n)\) поширюватися\(\mathbb{R}\) на дійсні числа, і це як позитивне, так і зменшується на\([1,\infty)\), то збіжність\( \sum\limits_{n=1}^\infty a_n\) така ж, як\(\int\limits_1^\infty a(x)dx\).

теорема\(\PageIndex{1}\): integral test

Нехай послідовність\(\{a_n\}\) буде визначена\(a_n=a(n)\), де\(a(n)\) є безперервним, додатним і зменшується на\([1,\infty)\). Потім\( \sum\limits_{n=1}^\infty a_n\) сходиться, якщо, і тільки якщо,\(\int\limits_1^\infty a(x) dx\) сходиться.

Ми можемо продемонструвати істинність інтегрального тесту з двома простими графіками. На\(\PageIndex{1a}\) малюнку висота кожного прямокутника\(a(n)=a_n\) для\(n=1,2,\ldots\), і явно прямокутники охоплюють більшу площу, ніж область під\(y=a(x)\). Тому можна зробити висновок, що

\[\int\limits_1^\infty a(x) dx < \sum\limits_{n=1}^\infty a_n.\label{eq:integral_testa}\]

Малюнок\(\PageIndex{1}\): Ілюстрація істини інтегрального тесту.

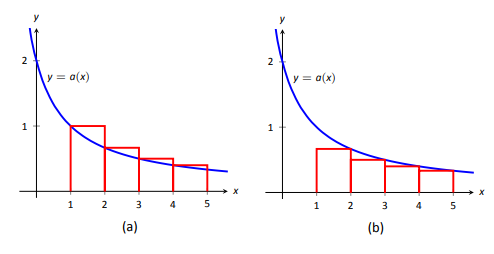
На\(\PageIndex{1b}\) малюнку малюємо прямокутники під\(y=a(x)\) правилом правої руки, починаючи з\(n=2\). На цей раз площа прямокутників менше площі під\(y=a(x)\), так\(\sum\limits_{n=2}^\infty a_n < \int\limits_1^\infty a(x) dx\). Зверніть увагу, з чого починається це підсумовування\(n=2\); додавання\(a_1\) до обох сторін дозволяє нам переписати підсумовування, починаючи з\(n=1\):

\[\sum\limits_{n=1}^\infty a_n < a_1 +\int\limits_1^\infty a(x) dx.\label{eq:integral_testb}\]

Поєднуючи рівняння\ ref {eq:integral_testa} і\ ref {eq:integral_testb}, ми маємо

\[\sum\limits_{n=1}^\infty a_n< a_1 +\int\limits_1^\infty a(x) dx < a_1 + \sum\limits_{n=1}^\infty a_n.\label{eq:integral_testc}\]

Теорема\(\PageIndex{1}\)

З Рівняння\ ref {eq:integral_testc} ми можемо зробити наступні два твердження:

1. Якщо\( \sum\limits_{n=1}^\infty a_n\) розходиться, так і робить\(\int\limits_1^\infty a(x) dx\) (тому що\( \sum\limits_{n=1}^\infty a_n < a_1 +\int\limits_1^\infty a(x) dx)\)
2. Якщо\( \sum\limits_{n=1}^\infty a_n\) сходиться, так і робить\(\int\limits_1^\infty a(x) dx\) (тому що\( \int\limits_1^\infty a(x) dx < \sum\limits_{n=1}^\infty a_n.)\)

Тому ряд і інтеграл або обидва сходяться, або обидва розходяться.

Теорема\(\PageIndex{1}\) дозволяє розширити цю теорему на ряди, де\(a(n)\) є додатною і зменшується\([b,\infty)\) для деяких\(b>1\).

Приклад\(\PageIndex{1}\): Using the Integral Test

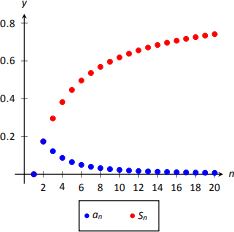
Визначаємо збіжність\(\sum\limits_{n=1}^\infty \dfrac{\ln n}{n^2}\). (Умови послідовності\(\{a_n\} = \{\ln n/n^2\}\) та n\(^{\text{th}}\) часткових сум наведені на малюнку\(\PageIndex{2}\)).

Рішення

Малюнок\(\PageIndex{2}\) має на увазі,\(a(n) = (\ln n)/n^2\) що позитивний і зменшується на\([2,\infty)\). Ми також можемо визначити це аналітично. Ми знаємо, що\(a(n)\) це позитивно, як\(\ln n\) і те\(n^2\), і інше, і позитивно\([2,\infty)\). Щоб визначити, що\(a(n)\) зменшується, розглянемо\(a^\prime(n) = (1-2\ln n)/n^3\), що є негативним для\(n\geq 2\). Так як\(a^\prime(n)\) негативний,\(a(n)\) то зменшується.

Малюнок\(\PageIndex{2}\): Побудова послідовності та рядів у прикладі\(\PageIndex{1}\).

Застосовуючи інтегральний тест, ми перевіряємо збіжність\( \int\limits_1^\infty \dfrac{\ln x}{x^2} dx\). Інтеграція цього неправильного інтеграла вимагає використання Інтеграція частинами, з\(u = \ln x\) і\(dv = 1/x^2 dx\).

\[\begin{align*}\int\limits_1^\infty \dfrac{\ln x}{x^2} dx &=\lim\limits_{b\to\infty} \int\limits_1^b \dfrac{\ln x}{x^2} dx\\ &=\lim\limits_{b\to\infty} -\dfrac1x\ln x\Big|_1^b + \int\limits_1^b\dfrac1{x^2} dx \\ &=\lim\limits_{b\to\infty} -\dfrac1x\ln x -\dfrac 1x\Big|_1^b\\ &=\lim\limits_{b\to\infty}1-\dfrac1b-\dfrac{\ln b}{b}.\quad \text{Apply L'H\(\hat o\)pital's Rule:}\\ &= 1. \end{align*}\]

Оскільки\( \int\limits_1^\infty \dfrac{\ln x}{x^2} dx\) сходиться, так і відбувається\( \sum\limits_{n=1}^\infty \dfrac{\ln n}{n^2}\).

Теорема 61 була дана без обґрунтування, стверджуючи, що загальний\(p\) -ряд\( \sum\limits_{n=1}^\infty \dfrac 1{(an+b)^p}\) сходиться якщо, і тільки якщо,\(p>1\). У наступному прикладі ми доведемо, що це правда, застосовуючи інтегральний тест.

Приклад\(\PageIndex{2}\): Using the Integral Test to establish Theorem 61

Використовуйте інтегральний тест, щоб довести, що\( \sum\limits_{n=1}^\infty \dfrac1{(an+b)^p}\) сходиться, якщо, і тільки якщо,\(p>1\).

Рішення

Розглянемо інтеграл\(\int\limits_1^\infty \dfrac1{(ax+b)^p} dx\); припускаючи\(p\neq 1\),

\ [\ почати {вирівнювати*}
\ int\ limits_1^\ infty\ dfrac1 {(ax+b) ^p} дх &=\ lim\ limits_ {c\ to\ infty}\ int\ limits_1^c\ dfrac1 {(ax+b) ^p} дх\\
&=\ lim\ limits_ {c\ to\ infty}\ dfrac {1} {a (1-p)} (ax+b) ^ {1-р}\ big|_1^c\\
&=\ lim\ limits_ {c\ to\ infty}\ dfrac {1} {a (1-p)}\ великий ((ac+b) ^ {1-p} - ( а+б) ^ {1-р}\ великий).
\ end {вирівнювати*}\]

Ця межа сходиться якщо, і тільки якщо,\(p>1\). Легко показати, що інтеграл також розходиться у випадку\(p=1\). (Цей результат схожий на роботу, що передувала Key Idea 21.)

Тому\( \sum\limits_{n=1}^\infty \dfrac 1{(an+b)^p}\) сходиться якщо, і тільки якщо,\(p>1\).

Ми розглянемо ще два тести збіжності в цьому розділі, обидва тести порівняння. Тобто ми визначаємо збіжність одного ряду, порівнюючи його з іншим рядом з відомою збіжністю.

Тест прямого порівняння

теорема\(\PageIndex{1}\): direct comparison test

\(\{b_n\}\)Дозволяти\(\{a_n\}\) і бути позитивними послідовностями, де\(a_n\leq b_n\) для всіх\(n\geq N\), для деяких\(N\geq 1\).

1. Якщо\( \sum\limits_{n=1}^\infty b_n\) сходиться, то\( \sum\limits_{n=1}^\infty a_n\) сходиться.
2. Якщо\( \sum\limits_{n=1}^\infty a_n\) розходиться, то\( \sum\limits_{n=1}^\infty b_n\) розходиться.

Примітка: Послідовність\(\{a_n\}\) є позитивною послідовністю, якщо\(a_n>0\) для всіх\(n\).

Через теорему 64, будь-яка теорема, яка спирається на позитивну послідовність, все ще має значення, коли\(a_n>0\) для всіх, крім кінцевого числа значень\(n\).

Приклад\(\PageIndex{3}\): Applying the Direct Comparison Test

Визначаємо збіжність\(\sum\limits_{n=1}^\infty \dfrac1{3^n+n^2}\).

Рішення

Ця серія не є ні геометричною, ні\(p\) -серією, але здається спорідненою. Ми прогнозуємо, що він сходиться, тому шукаємо ряд з більшими термінами, які сходяться. (Зверніть увагу, що інтегральний тест здається важким для застосування тут.)

Так як\(3^n < 3^n+n^2\),\( \dfrac1{3^n}> \dfrac1{3^n+n^2}\) для всіх\(n\geq1\). Ряд\(\sum\limits_{n=1}^\infty \dfrac{1}{3^n}\) є збіжним геометричним рядом; за теоремою 66,\( \sum\limits_{n=1}^\infty \dfrac1{3^n+n^2}\) сходиться.

Приклад\(\PageIndex{4}\): Applying the Direct Comparison Test

Визначаємо збіжність\(\sum\limits_{n=1}^\infty \dfrac{1}{n-\ln n}\).

Рішення

Ми знаємо, що серія гармонік\(\sum\limits_{n=1}^\infty \dfrac1n\) розходиться, і здається, що дана серія тісно пов'язана з нею, тому ми прогнозуємо, що вона буде розходитися.

Так як\(n\geq n-\ln n\) для всіх\(n\geq 1\),\( \dfrac1n \leq \dfrac1{n-\ln n}\) для всіх\(n\geq 1\).

Гармонічна серія розходиться, тому ми робимо висновок, що також\(\sum\limits_{n=1}^\infty \dfrac{1}{n-\ln n}\) розходиться.

Концепція прямого порівняння потужна і часто відносно проста у застосуванні. Практика допомагає розвинути необхідну інтуїцію, щоб швидко підібрати правильний ряд, з яким можна порівняти. Однак легко побудувати серію, для якої важко застосувати тест прямого порівняння.

Розглянемо\(\sum\limits_{n=1}^\infty \dfrac1{n+\ln n}\). Він дуже схожий на розбіжні ряди, наведені в прикладі 8.3.5. Підозрюємо, що він також розходиться, як\( \dfrac 1n \approx \dfrac1{n+\ln n}\) для великих\(n\). Однак нерівність, яку ми, природно, хочемо використовувати, «йде неправильним шляхом»: оскільки\(n\leq n+\ln n\) для всіх\(n\geq 1\),\(\dfrac1n \geq \dfrac{1}{n+\ln n}\) для всіх\(n\geq 1\). Дана серія має терміни менше, ніж терміни дивергентного ряду, і ми не можемо нічого з цього зробити висновок.

На щастя, ми можемо застосувати ще один тест до даного ряду, щоб визначити його збіжність.

Тест порівняння великих лімітів

Теорема 67: тест граничного порівняння

\(\{b_n\}\)Дозволяти\(\{a_n\}\) і бути позитивними послідовностями.

1. Якщо\(\lim_{n\to\infty} \dfrac{a_n}{b_n} = L\), де\(L\) є додатне дійсне число, то\( \sum\limits_{n=1}^\infty a_n\) і\( \sum\limits_{n=1}^\infty b_n\) інше сходяться або обидва розходяться.
2. Якщо\(\lim_{n\to\infty} \dfrac{a_n}{b_n} = 0\), то якщо\( \sum\limits_{n=1}^\infty b_n\) сходиться, то так і відбувається\( \sum\limits_{n=1}^\infty a_n\).
3. Якщо\(\lim_{n\to\infty} \dfrac{a_n}{b_n} = \infty\), то якщо\( \sum\limits_{n=1}^\infty b_n\) розходиться, то так і відбувається\( \sum\limits_{n=1}^\infty a_n\).

Теорема 67 найбільш корисна, коли\(\{b_n\}\) відома збіжність ряду з і ми намагаємося визначити збіжність ряду з\(\{a_n\}\).

Ми використовуємо тест порівняння лімітів у наступному прикладі, щоб вивчити серію,\(\sum\limits_{n=1}^\infty \dfrac1{n+\ln n}\) яка мотивувала цей новий тест.

Приклад\(\PageIndex{5}\): Applying the Limit Comparison Test

Визначте збіжність за\(\sum\limits_{n=1}^\infty \dfrac1{n+\ln n}\) допомогою тесту порівняння лімітів.

Рішення

Порівнюємо члени\(\sum\limits_{n=1}^\infty \dfrac1{n+\ln n}\) до членів гармонійної послідовності\(\sum\limits_{n=1}^\infty \dfrac1{n}\):

\ [\ begin {align*}
\ lim_ {n\ to\ infty}\ dfrac {1/ (n+\ ln n)} {1/n} &=\ lim\ limits_ {n\ to\ infty}\ dfrac {n} {n+\ ln n}\\
&= 1\ quad\ text {(після застосування правила L'H\(\hat o\) pital)}.
\ end {вирівнювати*}\]

Оскільки серія гармонік розходиться, ми робимо висновок, що також\(\sum\limits_{n=1}^\infty \dfrac1{n+\ln n}\) розходиться.

Приклад\(\PageIndex{6}\): Applying the Limit Comparison Test

Визначаємо збіжність\(\sum\limits_{n=1}^\infty \dfrac1{3^n-n^2}\)

Рішення
Цей ряд схожий на той, що в прикладі 8.3.3, але зараз ми розглядаємо\(3^n-n^2\) "" замість "»\(3^n+n^2\). Ця різниця ускладнює застосування тесту прямого порівняння.

Замість цього ми використовуємо тест порівняння лімітів і порівнюємо з серією\(\sum\limits_{n=1}^\infty \dfrac1{3^n}\):

\ [\ begin {align*}
\ lim_ {n\ to\ infty}\ dfrac {1/ (3^n-n^2)} {1/3^n} &=\ lim\ limits_ {n\ to\ infty}\ dfrac {3^n} {3^n-n^2}\\
&= 1\ квадратний\ текст {(після дворазового застосування правила L'H\(\hat o\) пітал)}.
\ end {вирівнювати*}\]

Ми знаємо\(\sum\limits_{n=1}^\infty \dfrac1{3^n}\), що це конвергентний геометричний ряд, отже, також\(\sum\limits_{n=1}^\infty \dfrac1{3^n-n^2}\) сходиться.

Як вже говорилося раніше, практика допомагає розвинути інтуїцію, щоб швидко вибрати серію, з якою порівнювати. Загальне правило полягає в тому, щоб вибрати ряд на основі домінуючого терміна у вираженні\(\{a_n\}\). Також корисно відзначити, що факторіали домінують експоненціальні, які домінують над алгебраїчними функціями (наприклад, поліномами), які домінують над логарифмами. У попередньому прикладі домінуючим терміном\(\dfrac{1}{3^n-n^2}\) було\(3^n\), тому ми порівняли ряд з\( \sum\limits_{n=1}^\infty \dfrac1{3^n}\). Однак важко застосувати тест порівняння обмежень до серій, що містять факторіали, оскільки ми не навчилися застосовувати правило L'H\(\hat o\) pital до\(n!\).

Приклад\(\PageIndex{7}\): Applying the Limit Comparison Test

Визначаємо збіжність\(\sum\limits_{n=1}^\infty \dfrac{\sqrt{n}+3}{n^2-n+1}\).

Рішення

Ми наївно намагаємося застосувати правило, наведене вище, і зауважимо, що домінуючим терміном у вираженні ряду є\(1/n^2\). Знаючи, що\( \sum\limits_{n=1}^\infty \dfrac1{n^2}\) сходиться, ми намагаємося застосувати тест порівняння лімітів:

\ [\ почати {вирівнювати*}
\ lim_ {n\ to\ infty}\ dfrac {(\ sqrt {n} +3)/(n^2-n+1)} {1/n^2} &=\ lim\ limits_ {n\ to\ infty}\ dfrac {n^2 (\ sqrt n+3)} {n^2-n+1}\
&=\ infty\ quad\ text {(Застосувати правило L'H\(\hat o\) pital)}.
\ end {вирівнювати*}\]

Теорема 67 частина (3) застосовується лише тоді, коли\(\sum\limits_{n=1}^\infty b_n\) розходиться; у нашому випадку вона сходиться. Зрештою, наш тест нічого не виявив про зближення нашої серії.

Проблема в тому, що ми вибрали бідну серію, з якою можна порівняти. Оскільки чисельник і знаменник членів ряду є одночасно алгебраїчними функціями, ми повинні були порівняти наш ряд з домінуючим терміном чисельника, розділеним на домінантний член знаменника.

Домінуючим терміном чисельника є\(n^{1/2}\) і домінуючим терміном знаменника є\(n^2\). Таким чином, слід порівняти терміни даного ряду з\(n^{1/2}/n^2 = 1/n^{3/2}\):

\ [\ почати {вирівнювати*}
\ lim_ {n\ to\ infty}\ dfrac {(\ sqrt {n} +3)/(n^2-n+1)} {1/n^ {3/2}} &=\ lim\ limits_ {n\ to\ infty}\ dfrac {n^ {3/2} (\ sqrt n+3)} {n^2-n+1}\
&= 1\ quad\ text {(Застосувати правило L'H\(\hat o\) pital)}.
\ end {вирівнювати*}\]

Оскільки\(p\) -ряд\(\sum\limits_{n=1}^\infty \dfrac1{n^{3/2}}\) сходиться, ми робимо висновок, що також\(\sum\limits_{n=1}^\infty \dfrac{\sqrt{n}+3}{n^2-n+1}\) сходиться.

Ми згадували раніше, що інтегральний тест не працює добре з серіями, що містять факторіальні терміни. Наступний розділ представляє Ratio Test, який добре справляється з такими серіями. Ми також вводимо кореневий тест, який добре підходить для серій, де кожен термін піднімається до певної сили.

Автори та атрибуція

• Template:ContribApexCalc