9.4: Порівняльні тести
- Page ID
- 62240
- Використовуйте тест порівняння, щоб перевірити ряд на збіжність.
- Використовуйте тест порівняння лімітів для визначення збіжності ряду.
Ми бачили, що інтегральний тест дозволяє визначити збіжність або розбіжність ряду, порівнюючи його з пов'язаним неправильним інтегралом. У цьому розділі ми показуємо, як використовувати тести порівняння для визначення збіжності або розбіжності ряду, порівнюючи його з серією, збіжність чи розбіжність якого відомі. Зазвичай ці тести використовуються для визначення збіжності рядів, схожих на геометричні ряди або\(p\) -серії.
Порівняльний тест
У попередніх двох розділах ми розглянули два великих класи серій: геометричні ряди та\(p\) -серії. Ми точно знаємо, коли ці ряди сходяться і коли розходяться. Тут ми показуємо, як використовувати збіжність або розбіжність цих рядів для доказу збіжності або розбіжності для інших серій, використовуючи метод, який називається тестом порівняння.
Для прикладу розглянемо серію
\[\sum_{n=1}^∞\dfrac{1}{n^2+1}. \nonumber \]
Виглядає ця серія схожа на збіжну серію
\[\sum_{n=1}^∞\dfrac{1}{n^2} \nonumber \]
Оскільки члени в кожному з рядів позитивні, послідовність часткових сум для кожного ряду монотонно збільшується. Крім того, оскільки
\[0<\dfrac{1}{n^2+1}<\dfrac{1}{n^2} \nonumber \]
для всіх натуральних чисел\(n\)\(\displaystyle \sum^∞_{n=1}\dfrac{1}{n^2+1}\) задовольняє\(k^{\text{th}}\) часткова сума\(S_k\)
\[S_k=\sum_{n=1}^k\dfrac{1}{n^2+1}<\sum_{n=1}^k\dfrac{1}{n^2}<\sum_{n=1}^∞\dfrac{1}{n^2}. \nonumber \]
(Див. Малюнок\(\PageIndex{1a}\) і табл\(\PageIndex{1}\).) Так як ряд справа сходиться, послідовність\({S_k}\) обмежена вище. Зроблено висновок, що\({S_k}\) це монотонна зростаюча послідовність, яка обмежена вище. Тому за теоремою монотонної збіжності\({S_k}\) сходиться, і, таким чином
\[\sum_{n=1}^∞\dfrac{1}{n^2+1} \nonumber \]
сходиться.
Аналогічно розглянемо серію
\[\sum_{n=1}^∞\dfrac{1}{n−1/2}. \nonumber \]
Цей серіал схожий на розбіжну серію
\[\sum_{n=1}^∞\dfrac{1}{n}. \nonumber \]
Послідовність часткових сум для кожного ряду монотонно збільшується і
\[\dfrac{1}{n−1/2}>\dfrac{1}{n}>0 \nonumber \]
за кожне натуральне число\(n\). Тому\(k^{\text{th}}\) часткова\(S_k\) сума
\[ \sum^∞_{n=1}\dfrac{1}{n−1/2} \nonumber \]
задовольняє
\[S_k=\sum_{n=1}^k\dfrac{1}{n−1/2}>\sum_{n=1}^k\dfrac{1}{n}. \nonumber \]
(Див. Рисунок\(\PageIndex{1n}\) і таблицю\(\PageIndex{1}\)). Оскільки ряд\(\displaystyle \sum^∞_{n=1}\frac{1}{n}\) розходиться до нескінченності, послідовність часткових сум\(\displaystyle \sum^k_{n=1}\frac{1}{n}\) необмежена. Отже,\({S_k}\) є необмеженою послідовністю, а значить і розходиться. Ми робимо висновок, що
\[\sum_{n=1}^∞\dfrac{1}{n−1/2} \nonumber \]
розходиться.
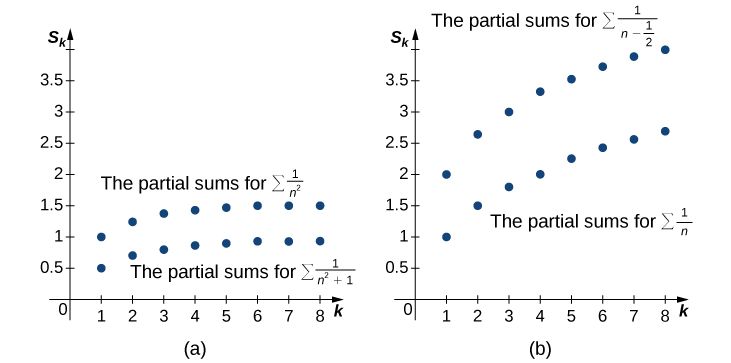
| \(k\) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| \(\displaystyle \sum_{n=1}^k\dfrac{1}{n^2+1}\) | 0.5 | 0.7 | 0.8 | 0.8588 | 0.8973 | 0,9243 | 0,9443 | 0,9597 |
| \(\displaystyle \sum_{n=1}^k\dfrac{1}{n^2}\) | 1 | 1,25 | 1,3611 | 1.4236 | 1,4636 | 1.4914 | 1.5118 | 1.5274 |
| \(k\) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| \(\displaystyle \sum_{n=1}^k\dfrac{1}{n−1/2}\) | 2 | 2.667 | 3.0667 | 3.3524 | 3.5746 | 3.7564 | 3.9103 | 4.0436 |
| \(\displaystyle \sum_{n=1}^k\dfrac{1}{n}\) | 1 | 1.5 | 1,8333 | 2.0933 | 2.2833 | 2.45 | 2.5929 | 2.7179 |
- Припустимо, існує ціле число\(N\) such that \(0≤a_n≤b_n\) for all \(n≥N\). If \(\displaystyle \sum^∞_{n=1}b_n\) converges, then \(\displaystyle \sum^∞_{n=1}a_n\) converges.
- Припустимо, існує ціле число\(N\) such that \(a_n≥b_n≥0\) for all \(n≥N.\) If \(\displaystyle \sum^∞_{n=1}b_n\) diverges, then \(\displaystyle \sum^∞_{n=1}a_n\) diverges.
Доведено, частина i. доказ частини II. є контрапозитивним частини i. нехай\({S_k}\) be the sequence of partial sums associated with \(\displaystyle \sum^∞_{n=1}a_n\), and let \(\displaystyle L=\sum^∞_{n=1}b_n\). Since the terms \(a_n≥0,\)
\[S_k=a_1+a_2+⋯+a_k≤a_1+a_2+⋯+a_k+a_{k+1}=S_{k+1}. \nonumber \]
Тому послідовність часткових сум збільшується. Далі, так як\(a_n≤b_n\) for all \(n≥N\), then
\[\sum_{n=N}^ka_n≤\sum_{n=N}^kb_n≤\sum_{n=1}^∞b_n=L. \nonumber \]
Тому для всіх\(k≥1\),
\[S_k=(a_1+a_2+⋯+a_{N−1})+\sum_{n=N}^ka_n≤(a_1+a_2+⋯+a_{N−1})+L. \nonumber \]
Так як\(a_1+a_2+⋯+a_{N−1}\) is a finite number, we conclude that the sequence \({S_k}\) is bounded above. Therefore, \({S_k}\) is an increasing sequence that is bounded above. By the Monotone Convergence Theorem, we conclude that \({S_k}\) converges, and therefore the series \(\displaystyle \sum_{n=1}^∞a_n\) converges.
□
Використовувати тест порівняння для визначення збіжності або розбіжності ряду\(\displaystyle \sum_{n=1}^∞a_n\), it is necessary to find a suitable series with which to compare it. Since we know the convergence properties of geometric series and \(p\)-series, these series are often used. If there exists an integer \(N\) such that for all \(n≥N\), each term an is less than each corresponding term of a known convergent series, then \(\displaystyle \sum_{n=1}^∞a_n\) converges. Similarly, if there exists an integer \(N\) such that for all \(n≥N\), each term an is greater than each corresponding term of a known divergent series, then \(\displaystyle \sum_{n=1}^∞a_n\) diverges.
Для кожної з наступних серій використовуйте тест порівняння, щоб визначити, чи збігається чи розходиться серія.
- \(\displaystyle \sum_{n=1}^∞=\dfrac{1}{n^3+3n+1}\)
- \(\displaystyle \sum_{n=1}^∞=\dfrac{1}{2^n+1}\)
- \(\displaystyle \sum_{n=2}^∞=\dfrac{1}{\ln \,n }\)
Рішення
а. порівняти з\(\displaystyle \sum_{n=1}^∞\dfrac{1}{n^3}\). Оскільки\(\displaystyle \sum_{n=1}^∞\dfrac{1}{n^3}\) це\(p\) -серія с\(p=3\), вона сходиться. Далі,
\[\dfrac{1}{n^3+3n+1}<\dfrac{1}{n^3} \nonumber \]
за кожне натуральне число\(n\). Тому можна зробити висновок, що\(\displaystyle \sum^∞_{n=1}\dfrac{1}{n^3+3n+1}\) сходиться.
б Порівняти з\(\displaystyle \sum^∞_{n=1}\left(\dfrac{1}{2}\right)^n\). Так як\(\displaystyle \sum_{n=1}^∞\left(\dfrac{1}{2}\right)^n\) це геометричний ряд з\(r=\dfrac{1}{2}\) і\(\left|\dfrac{1}{2}\right|<1\), він сходиться. Крім того,
\[\dfrac{1}{2^n+1}<\dfrac{1}{2^n} \nonumber \]
за кожне натуральне число\(n\). Тому ми бачимо, що\(\displaystyle \sum^∞_{n=1}\dfrac{1}{2^n+1}\) сходиться.
c Порівняти з\(\displaystyle \sum^∞_{n=2}\dfrac{1}{n}\). Так як
\[\dfrac{1}{\ln n }>\dfrac{1}{n} \nonumber \]
для кожного цілого числа\(n≥2\) і\(\displaystyle \sum^∞_{n=2}\dfrac{1}{n}\) розходиться, у нас є, що\(\displaystyle \sum^∞_{n=2}\dfrac{1}{\ln n}\) розходиться.
Використовуйте тест порівняння, щоб визначити, чи\(\displaystyle \sum^∞_{n=1}\dfrac{n}{n^3+n+1}\) збігається чи розходиться ряд.
- Підказка
-
Знайти значення\(p\) таке, що\(\dfrac{n}{n^3+n+1}≤\dfrac{1}{n^p}\).
- Відповідь
-
Серія сходиться.
Тест порівняння лімітів
Тест порівняння працює добре, якщо ми можемо знайти порівнянну серію, що задовольняє гіпотезу тесту. Однак іноді знайти відповідну серію може бути важко. Розглянемо серію
\[\sum_{n=2}^∞\dfrac{1}{n^2−1}. \nonumber \]
Цілком природно порівнювати цю серію з збіжною серією.
\[\sum_{n=2}^∞\dfrac{1}{n^2}. \nonumber \]
Однак ця серія не задовольняє гіпотезу, необхідну для використання тесту порівняння, оскільки
\[\dfrac{1}{n^2−1}>\dfrac{1}{n^2} \nonumber \]
для всіх цілих чисел\(n≥2\). Хоча ми могли б шукати іншу серію, з якою можна порівняти,\(\displaystyle \sum^∞_{n=2}\frac{1}{n^2−1},\) замість цього ми показуємо, як ми можемо використовувати тест порівняння лімітів для порівняння.
\[\sum_{n=2}^∞\frac{1}{n^2−1} \nonumber \]
і
\[\sum_{n=2}^∞\frac{1}{n^2}. \nonumber \]
Давайте розберемо ідею, що стоїть за тестом порівняння лімітів. Розглянемо два ряди\(\displaystyle \sum^∞_{n=1}a_n\)\(\displaystyle \sum^∞_{n=1}b_n\) і. з позитивними термінами\(a_n\) і\(b_n\) і оцінюємо
\[\lim_{n→∞}\frac{a_n}{b_n}. \nonumber \]
Якщо
\[\lim_{n→∞}\frac{a_n}{b_n}=L≠0, \nonumber \]
то, для\(n\) досить великих,\(a_n≈Lb_n\). Тому або обидва ряди сходяться, або обидва ряди розходяться. Для серіалу\(\displaystyle \sum^∞_{n=2}\frac{1}{n^2−1}\) і\(\displaystyle \sum^∞_{n=2}\dfrac{1}{n^2}\), ми бачимо, що
\[\lim_{n→∞}\dfrac{1/(n^2−1)}{1/n^2}=\lim_{n→∞}\dfrac{n^2}{n^2−1}=1. \nonumber \]
Оскільки\(\displaystyle \sum^∞_{n=2}\frac{1}{n^2}\) сходиться, робимо висновок, що
\[\sum_{n=2}^∞\dfrac{1}{n^2−1} \nonumber \]
сходиться.
Тест порівняння лімітів може бути використаний і в двох інших випадках. Припустимо
\[\lim_{n→∞}\dfrac{a_n}{b_n}=0. \nonumber \]
В даному випадку\({a_n/b_n}\) є обмеженою послідовністю. В результаті існує константа\(M\) така, що\(a_n≤Mb_n\). Тому якщо\(\displaystyle \sum^∞_{n=1}b_n\) сходиться, то\(\displaystyle \sum^∞_{n=1}a_n\) сходиться. З іншого боку, припустимо
\[\lim_{n→∞}\dfrac{a_n}{b_n}=∞. \nonumber \]
В даному випадку\({a_n/b_n}\) є необмеженою послідовністю. Тому для кожної\(M\) константи існує ціле число\(N\) таке, що\(a_n≥Mb_n\) для всіх\(n≥N.\) Тому якщо\(\displaystyle \sum^∞_{n=1}b_n\) розходиться, то і\(\displaystyle \sum^∞_{n=1}a_n\) розходиться.
Нехай\(a_n,b_n≥0\) для всіх\(n≥1.\)
- Якщо\(\displaystyle \lim_{n→∞}\frac{a_n}{b_n}=L≠0,\) потім\(\displaystyle \sum^∞_{n=1}a_n\) і\(\displaystyle \sum^∞_{n=1}b_n\) обидва сходяться або обидва розходяться.
- Якщо\(\displaystyle \lim_{n→∞}\frac{a_n}{b_n}=0\) і\(\displaystyle \sum^∞_{n=1}b_n\) сходиться, то\(\displaystyle \sum^∞_{n=1}a_n\) сходиться.
- Якщо\(\displaystyle \lim_{n→∞}\frac{a_n}{b_n}=∞\) і\(\displaystyle \sum^∞_{n=1}b_n\) розходиться, то\(\displaystyle \sum^∞_{n=1}a_n\) розходиться.
Зверніть увагу, що якщо\(\dfrac{a_n}{b_n}→0\) і\(\displaystyle \sum^∞_{n=1}b_n\) розходиться, тест порівняння лімітів не дає ніякої інформації. Аналогічно, якщо\(\dfrac{a_n}{b_n}→∞\) і\(\displaystyle \sum^∞_{n=1}b_n\) сходиться, тест також не дає ніякої інформації. Для прикладу розглянемо дві серії\(\displaystyle \sum_{n=1}^∞\frac{1}{\sqrt{n}}\) і\(\displaystyle \sum_{n=1}^∞\frac{1}{n^2}\). Ці серії обидва\(p\) -серії з\(p=\frac{1}{2}\) і\(p=2\), відповідно. Так як\(p=\frac{1}{2}<1,\) ряд\(\displaystyle \sum_{n=1}^∞\frac{1}{\sqrt{n}}\) розходиться. З іншого боку, з тих пір\(p=2>1\), ряд\(\displaystyle \sum_{n=1}^∞\frac{1}{n^2}\) сходиться. Однак, припустимо, ми спробували застосувати тест порівняння обмежень, використовуючи \(p\)збіжний −ряд\(\displaystyle \sum_{n=1}^∞\frac{1}{n^3}\) як наш ряд порівняння. По-перше, ми бачимо, що
\[\dfrac{1/\sqrt{n}}{1/n^3}=\dfrac{n^3}{\sqrt{n}}=n^{5/2}→∞\; \text{ as } \;n→∞. \nonumber \]
Точно так само ми бачимо, що
\[\dfrac{1/n^2}{1/n^3}=n→∞\; \text{ as } \;n→∞. \nonumber \]
Тому, якщо\(\dfrac{a_n}{b_n}→∞\) при\(\displaystyle \sum_{n=1}^∞b_n\) сходженні, ми не отримуємо ніякої інформації про зближення або розбіжність\(\displaystyle \sum_{n=1}^∞a_n\).
Для кожної з наступних серій використовуйте тест порівняння лімітів, щоб визначити, чи збігається чи розходиться серія. Якщо тест не застосовується, скажіть так.
- \(\displaystyle \sum^∞_{n=1}\dfrac{1}{\sqrt{n}+1}\)
- \(\displaystyle \sum^∞_{n=1}\dfrac{2^n+1}{3^n}\)
- \(\displaystyle \sum^∞_{n=1}\dfrac{\ln(n)}{n^2}\)
Рішення
а. Порівняйте цю серію з\(\displaystyle \sum^∞_{n=1}\dfrac{1}{\sqrt{n}}\). Розрахувати
\(\displaystyle \lim_{n→∞}\dfrac{1/(\sqrt{n}+1)}{1/\sqrt{n}}=\lim_{n→∞}\dfrac{\sqrt{n}}{\sqrt{n}+1}=\lim_{n→∞}\dfrac{1/\sqrt{n}}{1+1/\sqrt{n}}=1.\)
За граничним порівнянням тест, оскільки\(\displaystyle \sum^∞_{n=1}\dfrac{1}{\sqrt{n}}\) розходиться, то\(\displaystyle \sum^∞_{n=1}\dfrac{1}{\sqrt{n}+1}\) розходиться.
б) Порівняйте цю серію з\(\displaystyle \sum^∞_{n=1}\left(\dfrac{2}{3}\right)^n\). Ми бачимо, що
\(\displaystyle \lim_{n→∞}\dfrac{(2^n+1)/3^n}{2^n/3^n}=\lim_{n→∞}\dfrac{2^n+1}{3^n}⋅\dfrac{3^n}{2^n}=\lim_{n→∞}\dfrac{2^n+1}{2^n}=\lim_{n→∞}\left[1+\left(\tfrac{1}{2}\right)^n\right]=1.\)
Тому,
\(\displaystyle \lim_{n→∞}\dfrac{(2^n+1)/3^n}{2^n/3^n}=1.\)
Оскільки\(\displaystyle \sum^∞_{n=1}\left(\dfrac{2}{3}\right)^n\) сходиться, робимо висновок, що\(\displaystyle \sum^∞_{n=1}\dfrac{2^n+1}{3^n}\) сходиться.
c Оскільки\(\ln n<n,\) порівняйте с\(\displaystyle \sum^∞_{n=1}\dfrac{1}{n}\). Ми бачимо, що
\(\displaystyle \lim_{n→∞}\dfrac{\ln n/n^2}{1/n}=\lim_{n→∞}\dfrac{\ln n}{n^2}⋅\dfrac{n}{1}=\lim_{n→∞}\dfrac{\ln n}{n}.\)
Для того, щоб оцінити\(\displaystyle \lim_{n→∞}\ln n/n\), оцініть\(x→∞\) межу як дійсну функцію\(\ln(x)/x\). Ці два обмеження рівні, і внесення цієї зміни дозволяє нам використовувати правило L'Hôpital. Отримуємо
\(\displaystyle \lim_{x→∞}\dfrac{lnx}{x}=\lim_{x→∞}\dfrac{1}{x}=0.\)
Тому\(\displaystyle \lim_{n→∞}\frac{\ln n}{n}=0\), і, отже,
\(\displaystyle \lim_{n→∞}\dfrac{(\ln n)/n^2}{1/n}=0.\)
Оскільки\(0\) межа є, але\(\displaystyle \sum^∞_{n=1}\dfrac{1}{n}\) розходиться, тест порівняння лімітів не дає жодної інформації.
Порівняйте з\(\displaystyle \sum^∞_{n=1}\dfrac{1}{n^2}\) замість цього. У цьому випадку
\(\displaystyle \lim_{n→∞}\dfrac{(\ln n)/n^2}{1/n^2}=\lim_{n→∞}\dfrac{\ln n}{n^2}⋅\dfrac{n^2}{1}=\lim_{n→∞}\ln n=∞.\)
Оскільки\(∞\) межа є, але\(\displaystyle \sum^∞_{n=1}\dfrac{1}{n^2}\) сходиться, тест все одно не дає ніякої інформації.
Отже, тепер ми спробуємо ряд між двома, які ми вже пробували. Вибираючи серію\(\displaystyle \sum^∞_{n=1}\dfrac{1}{n^{3/2}}\), ми бачимо, що
\(\displaystyle \lim_{n→∞}\dfrac{(\ln n)/n^2}{1/n^{3/2}}=\lim_{n→∞}\dfrac{\ln n}{n^2}⋅\dfrac{n^{3/2}}{1}=\lim_{n→∞}\dfrac{\ln n}{\sqrt{n}}\).
Як і вище, для того\(\displaystyle \lim_{n→∞}\frac{\ln n}{\sqrt{n}}\), щоб оцінити, оцініть межу як\(x→∞\) дійсної функції\(\frac{\ln n}{\sqrt{n}}\). Використовуючи правило L'Hôpital,
\(\displaystyle \lim_{x→∞}\dfrac{\ln x}{\sqrt{x}}=\lim_{x→∞}\dfrac{2\sqrt{x}}{x}=\lim_{x→∞}\dfrac{2}{\sqrt{x}}=0\).
Так як\(0\) межа є і\(\displaystyle \sum^∞_{n=1}\dfrac{1}{n^{3/2}}\) сходиться, можна зробити висновок, що\(\displaystyle \sum^∞_{n=1}\dfrac{\ln n}{n^2}\) сходиться.
Використовуйте тест порівняння лімітів, щоб визначити, чи\(\displaystyle \sum^∞_{n=1}\dfrac{5^n}{3^n+2}\) збігається чи розходиться ряд.
- Підказка
-
Порівняйте з геометричним рядом.
- Відповідь
-
Серія розходиться.
Ключові концепції
- Тести порівняння використовуються для визначення збіжності або розбіжності рядів з позитивними показниками.
- При використанні порівняльних тестів ряд часто\(\displaystyle \sum^∞_{n=1}a_n\) порівнюють з геометричним або\(p\) -серією.
Глосарій
- порівняльний тест
- Якщо\(0≤a_n≤b_n\) для всіх\(n≥N\) і\(\displaystyle \sum^∞_{n=1}b_n\) сходиться, то\(\displaystyle \sum^∞_{n=1}a_n\) сходиться; якщо\(a_n≥b_n≥0\) для всіх\(n≥N\) і\(\displaystyle \sum^∞_{n=1}b_n\) розходиться, то\(\displaystyle \sum^∞_{n=1}a_n\) розходиться.
- граничний тест порівняння
- Припустимо\(a_n,b_n≥0\), для всіх\(n≥1\). Якщо\(\displaystyle \lim_{n→∞}a_n/b_n→L≠0\), то\(\displaystyle \sum^∞_{n=1}a_n\) і те й\(\displaystyle \sum^∞_{n=1}b_n\) інше сходяться або обидва розходяться; якщо\(\displaystyle \lim_{n→∞}a_n/b_n→0\) і\(\displaystyle \sum^∞_{n=1}b_n\) сходиться, то\(\displaystyle \sum^∞_{n=1}a_n\) сходиться. Якщо\(\displaystyle \lim_{n→∞}a_n/b_n→∞\), і\(\displaystyle \sum^∞_{n=1}b_n\) розходиться, то\(\displaystyle \sum^∞_{n=1}a_n\) розходиться.
