9.3: Дивергенція та інтегральні тести

Цілі навчання

• Використовуйте тест на розбіжність, щоб визначити, чи збігається чи розходиться ряд.
• Використовуйте інтегральний тест для визначення збіжності ряду.
• Оцініть значення ряду, знайшовши межі його залишку.

У попередньому розділі ми визначили збіжність або розбіжність декількох рядів шляхом явного обчислення межі послідовності часткових сум. На\( {S_k}.\) практиці явний розрахунок цієї межі може бути складним або неможливим. На щастя, існує кілька тестів, які дозволяють визначити конвергенцію або розбіжність для багатьох типів серій. У цьому розділі ми обговорюємо два з цих тестів: тест на дивергенцію та інтегральний тест. Ми розглянемо кілька інших тестів в решті цієї глави, а потім підсумуємо, як і коли їх використовувати.

Тест на розбіжність

Для зближення ряду\(\displaystyle \sum^∞_{n=1}a_n\)\( n^{th}\) термін\( a_n\) повинен задовольняти,\( a_n→0\) як\( n→∞.\) Отже, з алгебраїчних граничних властивостей послідовностей,

\[\begin{align*} \lim_{k→∞}a_k = \lim_{k→∞}(S_k−S_{k−1}) \\[4pt] =\lim_{k→∞}S_k−\lim_{k→∞}S_{k−1} \\[4pt] =S−S=0. \end{align*}\]

Тому, якщо\(\displaystyle \sum_{n=1}^∞a_n\) сходиться,\( n^{th}\) термін\( a_n→0\) як\( n→∞.\) важливим наслідком цього факту є наступне твердження:

Якщо\( a_n↛0\) як\(\displaystyle n→∞,\sum_{n=1}^∞a_n\) розходиться.

Цей тест відомий як тест на розбіжність, оскільки він забезпечує спосіб довести, що серія розходиться.

Визначення: Тест на розбіжність

Якщо\(\displaystyle \lim_{n→∞}a_n=c≠0\) або\(\displaystyle \lim_{n→∞}a_n\) немає, то ряд\(\displaystyle \sum_{n=1}^∞a_n\) розходиться.

Важливо відзначити, що зворотне значення цієї теореми не відповідає дійсності. Тобто, якщо\(\displaystyle \lim_{n→∞}a_n=0\), ми не можемо зробити жодного висновку про зближення\(\displaystyle \sum_{n=1}^∞a_n\).

Наприклад\(\displaystyle \lim_{n→0}\tfrac{1}{n}=0\), але гармонійний ряд\(\displaystyle \sum^∞_{n=1}\frac{1}{n}\) розходиться. У цьому розділі та інших розділах цієї глави ми покажемо ще багато прикладів таких серій. Отже, хоча ми можемо використовувати тест на розбіжність, щоб показати, що серія розходиться, ми не можемо використовувати його, щоб довести, що серія сходиться. Зокрема, якщо\( a_n→0\), тест на розбіжність є безрезультатним.

Приклад\( \PageIndex{1}\): Using the divergence test

Для кожного з наступних рядів застосуйте тест на розбіжність. Якщо тест на розбіжність доведе, що ряд розходиться, вкажіть так. В іншому випадку вкажіть, що тест на розбіжність є безрезультатним.

1. \(\displaystyle \sum^∞_{n=1}\frac{n}{3n−1}\)
2. \(\displaystyle \sum^∞_{n=1}\frac{1}{n^3}\)
3. \(\displaystyle \sum^∞_{n=1}e^{1/n^2}\)

Рішення

1. Так як\(\displaystyle \lim_{n→∞} \frac{n}{3n−1}=\frac{1}{3}≠0\), шляхом тесту на розбіжність, можна зробити висновок, що\(\displaystyle \sum_{n=1}^∞\dfrac{n}{3n−1}\) розходиться.
2. Оскільки\(\displaystyle \lim_{n→∞} \frac{1}{n^3}=0\) тест на розбіжність є безрезультатним.
3. Так як\(\displaystyle \lim_{n→∞} e^{1/n^2}=1≠0\) за тестом на розбіжність ряд\(\displaystyle \sum_{n=1}^∞e^{1/n^2}\) розходиться.

Вправа\( \PageIndex{1}\)

Що говорить нам тест на дивергенцію про серіал\(\displaystyle \sum_{n=1}^∞\cos(1/n^2)\)?

Підказка

Подивіться на\(\displaystyle \lim_{n→∞}\cos(1/n^2)\).

Відповідь

Серія розходиться.

Інтегральний тест

У попередньому розділі ми довели, що гармонічний ряд розходиться, дивлячись на послідовність часткових сум\( {S_k}\) і показуючи, що\( S_{2^k}>1+k/2\) для всіх натуральних чисел\( k\). У цьому розділі ми використовуємо іншу техніку, щоб довести розбіжність гармонійного ряду. Ця методика важлива, оскільки використовується для доведення розбіжності або зближення багатьох інших серій. Цей тест, званий інтегральним тестом, порівнює нескінченну суму з неправильним інтегралом. Важливо зазначити, що цей тест можна застосовувати лише тоді, коли ми розглядаємо серію, терміни якої є позитивними.

Малюнок\(\PageIndex{1}\): Сума площ прямокутників більша за площу між кривою\( f(x)=1/x\) і\( x\) -віссю для\( x≥1\). Оскільки площа, обмежена кривою, нескінченна (як обчислюється неправильним інтегралом), сума площ прямокутників також нескінченна.

Щоб проілюструвати, як працює інтегральний тест, використовуйте гармонічний ряд як приклад. На малюнку зображуємо гармонійний ряд\(\PageIndex{1}\), намалювавши послідовність прямокутників з областями\( 1,1/2,1/3,1/4,…\) разом з функцією.\( f(x)=1/x.\) З графіка ми бачимо, що

\[\sum_{n=1}^k\dfrac{1}{n}=1+\dfrac{1}{2}+\dfrac{1}{3}+⋯+\dfrac{1}{k}>∫^{k+1}_1\dfrac{1}{x}\,dx. \nonumber \]

Тому для кожного\( k\)\( S_k\) задовольняє\( k^{\text{th}}\) часткова сума

\[\begin{align*} S_k =\sum_{n=1}^k\dfrac{1}{n} >∫^{k+1}_1\dfrac{1}{x}\,dx = \ln x \big| ^{k+1}_1 \\[4pt] = \ln (k+1)−\ln (1) \\[4pt] =\ln (k+1).\end{align*}\]

Оскільки\(\displaystyle \lim_{k→∞}\ln(k+1)=∞,\) ми бачимо, що послідовність часткових сум\( {S_k}\) необмежена. Тому\( {S_k}\) розходиться, а, отже, і ряд\(\displaystyle \sum_{n=1}^∞\dfrac{1}{n}\) теж розходиться.

Малюнок\(\PageIndex{2}\): Сума площ прямокутників менше суми площі першого прямокутника і площі між кривою\( f(x)=1/x^2\) і\( x\) -віссю для\( x≥1\). Оскільки площа, обмежена кривою, є кінцевою, сума площ прямокутників також кінцева.

Тепер розглянемо серію\(\displaystyle \sum_{n=1}^∞\frac{1}{n^2}\). Показано, як інтеграл можна використовувати, щоб довести, що цей ряд сходиться. На малюнку\(\PageIndex{2}\) ми накидаємо послідовність прямокутників з областями\( 1,1/2^2,1/3^2,…\) разом з функцією\( f(x)=\frac{1}{x^2}\). З графіка ми бачимо, що

\[\sum_{n=1}^k\dfrac{1}{n^2}=1+\dfrac{1}{2^2}+\dfrac{1}{3^2}+⋯+\dfrac{1}{k^2}<1+∫^k_1\dfrac{1}{x^2}\,dx. \nonumber \]

Тому для кожного\( k\)\( S_k\) задовольняє\( k^{\text{th}}\) часткова сума

\[\begin{align*} S_k=\sum_{n=1}^k\dfrac{1}{n^2}<1+∫^k_1\dfrac{1}{x^2}\,dx =1−\left. \dfrac{1}{x} \right|^k_1 \\[4pt] =1−\dfrac{1}{k}+1 \\[4pt] =2−\dfrac{1}{k}<2. \end{align*}\]

Зроблено висновок, що послідовність часткових сум\( {S_k}\) обмежена. Ми також бачимо, що\( {S_k}\) це зростаюча послідовність:

\[S_k=S_{k−1}+\dfrac{1}{k^2} \nonumber \]

для\( k≥2\).

Оскільки\( {S_k}\) збільшується і обмежується, за теоремою монотонної збіжності вона сходиться. Тому ряд\(\displaystyle \sum_{n=1}^∞\frac{1}{n^2}\) сходиться.

Рисунок\(\PageIndex{3}\): (а) Якщо ми можемо вписати прямокутники всередині області, обмеженої кривою\( y=f(x)\) і\( x\) -віссю, і площа, обмежена цими кривими для,\( x≥1\) є кінцевою, то сума площ прямокутників також кінцева. (b) Якщо набір прямокутників обмежує область, обмежену\( x\) віссю для\( x≥1\),\( y=f(x)\) а область має нескінченну площу, то сума площ прямокутників також нескінченна.

Ми можемо розширити цю ідею, щоб довести конвергенцію або розбіжність для багатьох різних серій. Припустимо,\(\displaystyle \sum^∞_{n=1}a_n\) це ряд з додатними\( a_n\) членами, такими, що існує неперервна, додатна, спадна функція\( f\) де\( f(n)=a_n\) для всіх натуральних чисел. Тоді, як на малюнку\(\PageIndex{3a}\), для будь-якого цілого числа\( k\)\( k^{\text{th}}\) часткова сума\( S_k\) задовольняє

\[S_k=a_1+a_2+a_3+⋯+a_k<a_1+∫^k_1f(x)\,dx<1+∫^∞_1f(x)\,dx. \nonumber \]

Тому якщо\(\displaystyle ∫^∞_1f(x)\,dx\) сходиться, то послідовність часткових сум\( {S_k}\) обмежена. Оскільки\( {S_k}\) є зростаючою послідовністю, якщо це також обмежена послідовність, то за теоремою монотонної збіжності вона сходиться. Робимо висновок, що якщо\(\displaystyle ∫^∞_1f(x)\,dx\) сходиться, то\(\displaystyle \sum^∞_{n=1}a_n\) і ряд сходиться. З іншого боку, з малюнка\(\PageIndex{3b}\), для будь-якого цілого числа\( k\),\( k^{\text{th}}\) часткова сума\( S_k\) задовольняє

\[S_k=a_1+a_2+a_3+⋯+a_k>∫^{k+1}_1f(x)\,dx. \nonumber \]

Якщо

\[ \lim_{k→∞}∫^{k+1}_1f(x)\,dx=∞, \nonumber \]

то\( {S_k}\) є необмеженою послідовністю і тому розходиться. В результаті ряд\(\displaystyle \sum_{n=1}^∞a_n\) також розходиться. Так як\( f\) є позитивною функцією, якщо\(\displaystyle ∫^∞_1f(x)\,dx\) розходиться, то

\[ \lim_{k→∞}∫^{k+1}_1f(x)\,dx=∞. \nonumber \]

Робимо висновок, що якщо\(\displaystyle ∫^∞_1f(x)\,dx\) розходиться, то\(\displaystyle \sum_{n=1}^∞a_n\) розходиться.

Визначення: Інтегральний тест

Припустимо,\(\displaystyle \sum_{n=1}^∞a_n\) це ряд з позитивними термінами\( a_n\). Припустимо, існує функція\( f\) і додатне ціле число\( N\) такі, що виконуються наступні три умови:

1. \( f\)є безперервним,
2. \( f\)зменшується, і
3. \( f(n)=a_n\)для всіх цілих чисел\( n≥N.\)

Тоді

\[\sum_{n=1}^∞a_n \nonumber \]

і

\[∫^∞_Nf(x)\,dx \nonumber \]

обидва сходяться або обидва розходяться (рис.\(\PageIndex{3}\)).

Хоча конвергенція\(\displaystyle ∫^∞_Nf(x)\,dx\) має на увазі зближення спорідненого ряду\(\displaystyle \sum_{n=1}^∞a_n\), це не означає, що значення інтеграла та ряду однакові. Вони можуть бути різними, а часто бувають. Наприклад,

\[\sum_{n=1}^∞\left(\dfrac{1}{e}\right)^n=\dfrac{1}{e}+\left(\dfrac{1}{e}\right)^2+\left(\dfrac{1}{e}\right)^3+⋯ \nonumber \]

геометричний ряд з початковим терміном\( a=1/e\) і співвідношенням\( r=1/e,\), який сходиться до

\[\dfrac{1/e}{1−(1/e)}=\dfrac{1/e}{(e−1)/e}=\dfrac{1}{e−1}. \nonumber \]

Однак споріднений інтеграл\(\displaystyle ∫^∞_1(1/e)^x\,dx\) задовольняє

\[∫^∞_1\left(\frac{1}{e}\right)^x\,dx=∫^∞_1e^{−x}\,dx=\lim_{b→∞}∫^b_1e^{−x}\,dx=\lim_{b→∞}−e^{−x}\big|^b_1=\lim_{b→∞}[−e^{−b}+e^{−1}]=\dfrac{1}{e}. \nonumber \]

Приклад\( \PageIndex{2}\): Using the Integral Test

Для кожної з наступних серій використовуйте інтегральний тест, щоб визначити, сходиться чи розходиться ряд.

1. \(\displaystyle \sum_{n=1}^∞\frac{1}{n^3}\)
2. \(\displaystyle \sum^∞_{n=1}\frac{1}{\sqrt{2n−1}}\)

Рішення

a. порівняти

\(\displaystyle \sum_{n=1}^∞\dfrac{1}{n^3}\)і\(\displaystyle ∫^∞_1\dfrac{1}{x^3}\,dx.\)

У нас є

\(\displaystyle ∫^∞_1\dfrac{1}{x^3}\,dx=\lim_{b→∞}∫^b_1\dfrac{1}{x^3}\,dx=\lim_{b→∞}\left[−\dfrac{1}{2x^2}\bigg|^b_1\right]=\lim_{b→∞}\left[−\dfrac{1}{2b^2}+\dfrac{1}{2}\right]=\dfrac{1}{2}.\)

Таким чином інтеграл\(\displaystyle ∫^∞_1\frac{1}{x^3}\,dx\) сходиться, а отже, і ряд

\(\displaystyle \sum_{n=1}^∞\dfrac{1}{n^3}\).

б. порівняти

\(\displaystyle \sum_{n=1}^∞\dfrac{1}{\sqrt{2n−1}}\)і\(\displaystyle ∫^∞_1\dfrac{1}{\sqrt{2x−1}}\,dx\).

Так як

\(\displaystyle ∫^∞_1\frac{1}{\sqrt{2x−1}}\,dx=\lim_{b→∞}∫^b_1\frac{1}{\sqrt{2x−1}}\,dx=\lim_{b→∞}\sqrt{2x−1}\bigg|^b_1=\lim_{b→∞}\left[\sqrt{2b−1}−1\right]=∞,\)

інтеграл\(\displaystyle ∫^∞_1\frac{1}{\sqrt{2x−1}}\,dx\) розходиться, і тому

\(\displaystyle \sum_{n=1}^∞\frac{1}{\sqrt{2n−1}}\)

розходиться.

Вправа\( \PageIndex{2}\)

Використовуйте інтегральний тест, щоб визначити,\(\displaystyle \sum^∞_{n=1}\dfrac{n}{3n^2+1}\) сходиться чи розходиться ряд.

Підказка

Порівняти з інтегралом\(\displaystyle ∫^∞_1\dfrac{x}{3x^2+1}\,dx.\)

Відповідь

Серія розходиться.

\(p\)Серія

Гармонічний ряд\(\displaystyle \sum^∞_{n=1}1/n\) і ряд\(\displaystyle \sum^∞_{n=1}1/n^2\) є прикладами типу рядів, які називаються p-серією.

Визначення:\(p\)-series

Для будь-якого дійсного числа\( p\), ряд

\[\sum_{n=1}^∞\dfrac{1}{n^p} \nonumber \]

називається p-серією.

Ми знаємо, що\(p\) -серія сходиться, якщо\( p=2\) і розходиться, якщо\( p=1\). А як щодо інших цінностей\( p\)? Взагалі, важко, якщо не неможливо, обчислити точне значення більшості\( p\) -рядів. Однак ми можемо використовувати тести, представлені до цих пір, щоб довести, чи сходиться чи розходиться\( p\) -серія.

Якщо\( p<0,\) тоді\( 1/n^p→∞,\) і якщо\( p=0\), то\( 1/n^p→1.\) Тому, шляхом випробування розбіжності,

\[\sum_{n=1}^∞\dfrac{1}{n^p} \nonumber \]

розходиться якщо\(p≤0\).

Якщо\( p>0,\)\( f(x)=1/x^p\) то позитивна, безперервна, спадна функція. Тому для\( p>0,\) нас використовується інтегральний тест, порівнюючи

\[\sum_{n=1}^∞\dfrac{1}{n^p} \nonumber \]і\[∫^∞_1\dfrac{1}{x^p}\,dx. \nonumber \]

Ми вже розглядали випадок, коли\( p=1.\) Тут ми розглядаємо випадок, коли\( p>0,p≠1.\) Для цього випадку,

\[∫^∞_1\dfrac{1}{x^p}\,dx=\lim_{b→∞}∫^b_1\dfrac{1}{x^p}\,dx=\lim_{b→∞}\dfrac{1}{1−p}x^{1−p}∣^b_1=\lim_{b→∞}\dfrac{1}{1−p}[b^{1−p}−1]. \nonumber \]

Тому що

\( b^{1−p}→0\)якщо\( p>1\) і\( b^{1−p}→∞\) якщо\( p<1,\)

робимо висновок, що

\[∫^∞_1\dfrac{1}{x^p}\,dx=\begin{cases}\dfrac{1}{p−1}, \text{if}\;p>1\\ ∞, \text{if}\;p<1.\end{cases} \nonumber \]

Тому\(\displaystyle \sum^∞_{n=1}1/n^p\) сходиться якщо\( p>1\) і розходиться, якщо\( 0<p<1.\)

Підсумовуючи,

\[\sum_{n=1}^∞\dfrac{1}{n^p}\quad \begin{cases}\text{converges} \text{if}\; p>1\\ \text{diverges} \text{if}\;p≤1\end{cases} \nonumber \].

Приклад\( \PageIndex{3}\): Testing for Convergence of p-series

Для кожного з наступних рядів визначте, сходиться він або розходиться.

1. \(\displaystyle \sum^∞_{n=1}\dfrac{1}{n^4}\)
2. \(\displaystyle \sum^∞_{n=1}\dfrac{1}{n^{2/3}}\)

Рішення

1. Це\(p\) -серія с\( p=4>1\), тому серія сходиться.
2. Так як\( p=2/3<1,\) ряд розходиться.

Вправа\( \PageIndex{3}\)

Серія\(\displaystyle \sum^∞_{n=1}\dfrac{1}{n^{5/4}}\) сходиться або розходиться?

Підказка

\( p=5/4\)

Відповідь

Серія сходиться.

Оцінка вартості ряду

Припустимо, ми знаємо, що серія\(\displaystyle \sum_{n=1}^∞a_n\) сходиться, і ми хочемо оцінити суму цього ряду. Звичайно, ми можемо наблизити цю суму, використовуючи будь-яку кінцеву суму\(\displaystyle \sum_{n=1}^Na_n\), де будь-яке\( N\) натуральне число. Питання, яке ми тут звертаємося, полягає в тому\(\displaystyle \sum^∞_{n=1}a_n\), наскільки добре це наближення\(\displaystyle \sum^N_{n=1}a_n\)?

Більш конкретно, якщо ми дозволимо

\[R_N=\sum_{n=1}^∞a_n−\sum_{n=1}^Na_n \nonumber \]

бути залишком, коли сума нескінченного ряду наближена\(N^{\text{th}}\) частковою сумою, наскільки велика\( R_N\)? Для деяких типів серій ми можемо використовувати ідеї з інтегрального тесту для оцінки\( R_N\).

Примітка\(\PageIndex{1}\): Remainder Estimate from the Integral Test

Припустимо,\(\displaystyle \sum^∞_{n=1}a_n\) це збіжний ряд з позитивними показниками. Припустимо, існує функція, яка\( f\) задовольняє наступним трьом умовам:

1. \( f\)є безперервним,
2. \( f\)зменшується, і
3. \( f(n)=a_n\)для всіх цілих чисел\( n≥1.\)

\( S_N\)Дозволяти\(N^{\text{th}}\) часткова сума\(\displaystyle \sum^∞_{n=1}a_n\). Для всіх натуральних чисел\( N\),

\[S_N+∫^∞_{N+1}f(x)\,dx<\sum_{n=1}^∞a_n<S_N+∫^∞_Nf(x)\,dx. \nonumber \]

Іншими словами, залишок\(\displaystyle R_N=\sum^∞_{n=1}a_n−S_N=\sum^∞_{n=N+1}a_n\) задовольняє наступну оцінку:

\[∫^∞_{N+1}f(x)\,dx<R_N<∫^∞_Nf(x)\,dx. \nonumber \]

Це відомо як оцінка залишку.

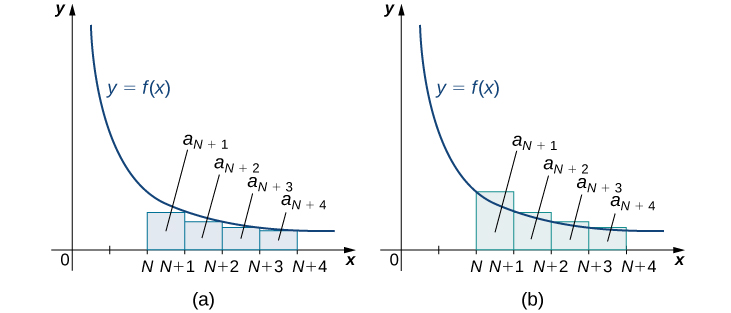
Проілюструємо\(\PageIndex{1}\) Примітку на рис\(\PageIndex{4}\). Зокрема, представляючи залишок\( R_N=a_{N+1}+a_{N+2}+a_{N+3}+⋯\) як суму площ прямокутників, ми бачимо, що площа цих прямокутників обмежена вище\(\displaystyle ∫^∞_Nf(x)\,dx\) і обмежена нижче\(\displaystyle ∫^∞_{N+1}f(x)\,dx.\) Іншими словами,

\[R_N=a_{N+1}+a_{N+2}+a_{N+3}+⋯>∫^∞_{N+1}f(x)\,dx \nonumber \]

і

\[R_N=a_{N+1}+a_{N+2}+a_{N+3}+⋯<∫^∞_Nf(x)\,dx. \nonumber \]

Ми робимо висновок, що

\[∫^∞_{N+1}f(x)\,dx<R_N<∫^∞_Nf(x)\,dx. \nonumber \]

Так як

\[\sum_{n=1}^∞a_n=S_N+R_N, \nonumber \]

де\( S_N\)\(N^{\text{th}}\) часткова сума, робимо висновок, що

\[S_N+∫^∞_{N+1}f(x)\,dx<\sum_{n=1}^∞a_n<S_N+∫^∞_Nf(x)\,dx. \nonumber \]

Рисунок\(\PageIndex{4}\): Задано неперервну, додатну, спадну функцію\( f\) та послідовність позитивних членів,\( a_n\) таких\( n\), що\( a_n=f(n)\) для всіх натуральних чисел, (a) області\(\displaystyle a_{N+1}+a_{N+2}+a_{N+3}+⋯<∫^∞_Nf(x)\,dx\), або (b) області\(\displaystyle a_{N+1}+a_{N+2}+a_{N+3}+⋯>∫^∞_{N+1}f(x)\,dx\). Тому інтеграл - це або завищення, або недооцінка похибки.

Приклад\( \PageIndex{4}\): Estimating the Value of a Series

Розглянемо серію\(\displaystyle \sum^∞_{n=1}\frac{1}{n^3}\).

1. Розрахувати\(\displaystyle S_{10}=\sum^{10}_{n=1}\frac{1}{n^3}\) і оцінити похибку.
2. Визначте найменшу величину\( N\) необхідного такого, що\( S_N\) буде\(\displaystyle \sum^∞_{n=1}\frac{1}{n^3}\) оцінювати в межах\( 0.001\).

Рішення

a. використовуючи обчислювальну утиліту, ми маємо

\[ S_{10}=1+\dfrac{1}{2^3}+\dfrac{1}{3^3}+\dfrac{1}{4^3}+⋯+\dfrac{1}{10^3}≈1.19753. \nonumber \]

За оцінкою, що залишилася, ми знаємо

\[ R_N<∫^∞_N\dfrac{1}{x^3}\,dx. \nonumber \]

У нас є

\[ ∫^∞_{10}\dfrac{1}{x^3}\,dx=\lim_{b→∞}∫^b_{10}\dfrac{1}{x^3}\,dx=\lim_{b→∞}\left[−\dfrac{1}{2x^2}\right]^b_N=\lim_{b→∞}\left[−\dfrac{1}{2b^2}+\dfrac{1}{2N^2}\right]=\dfrac{1}{2N^2}. \nonumber \]

Тому помилка є\( R_{10}<1/2(10)^2=0.005.\)

б. знайти\( N\) таке, що\( R_N<0.001\). Частково a. ми показали, що\( R_N<1/2N^2\). Тому залишок\( R_N<0.001\) стільки ж, скільки\( 1/2N^2<0.001\). Тобто нам потрібно\( 2N^2>1000\). Вирішуючи цю нерівність для\( N\), ми бачимо, що нам потрібно\( N>22.36\). Щоб залишок знаходився в межах потрібної суми, нам потрібно округлити до найближчого цілого числа. Тому мінімально необхідне значення є\( N=23\).

Вправа\( \PageIndex{4}\)

Для\(\displaystyle \sum^∞_{n=1}\frac{1}{n^4}\), обчислити\( S_5\) і оцінити похибку\( R_5\).

Підказка

Використовуйте оцінку залишку\(\displaystyle R_N<∫^∞_N\frac{1}{x^4}\,dx.\)

Відповідь

\( S_5≈1.09035, R_5<0.00267\)

Ключові концепції

• Якщо\(\displaystyle \lim_{n→∞}a_n≠0,\) потім ряд\(\displaystyle \sum^∞_{n=1}a_n\) розходиться.
• Якщо\(\displaystyle \lim_{n→∞}a_n=0,\) ряд\(\displaystyle \sum^∞_{n=1}a_n\) може сходитися або розходитися.
• Якщо\(\displaystyle \sum^∞_{n=1}a_n\) є рядом з додатними членами\( a_n\) і\( f\) є неперервною, спадною функцією такої, що\( f(n)=a_n\) для всіх натуральних чисел\( n\), то

\[\sum_{n=1}^∞a_n \nonumber \]і\[∫^∞_1f(x)\,dx \nonumber \]

або обидва сходяться, або обидва розходяться. Крім того, якщо\(\displaystyle \sum^∞_{n=1}a_n\) сходиться, то наближення\(N^{\text{th}}\) часткової суми\( S_N\) є точним аж до помилки\( R_N\) де\(\displaystyle ∫^∞_{N+1}f(x)\,dx<R_N<∫^∞_Nf(x)\,dx\).

• \(p\)Серія\(\displaystyle \sum_{n=1}^∞\frac{1}{n^p}\) -сходиться, якщо\( p>1\) і розходиться, якщо\( p≤1.\)

Ключові рівняння

• Тест на дивергенцію

Якщо\( a_n↛0\) як\(\displaystyle n→∞,\sum_{n=1}^∞a_n\) розходиться.

• p-серія

\(\displaystyle \sum_{n=1}^∞\dfrac{1}{n^p}\quad \begin{cases}\text{converges}, \text{if}\;p>1\\\text{diverges}, \text{if}\; p≤1\end{cases}\)

• Оцінка залишку від інтегрального тесту

\(\displaystyle ∫^∞_{N+1}f(x)\,dx<R_N<∫^∞_Nf(x)\,dx\)

Глосарій

тест на розбіжність

якщо\(\displaystyle \lim_{n→∞}a_n≠0,\) то ряд\(\displaystyle \sum^∞_{n=1}a_n\) розходиться

інтегральний тест

для ряду\(\displaystyle \sum^∞_{n=1}a_n\) з додатними членами\( a_n\), якщо існує неперервна, спадна функція\( f\) така, що\( f(n)=a_n\) для всіх натуральних чисел\( n\), то

\[\sum_{n=1}^∞a_n \nonumber \]і\[∫^∞_1f(x)\,dx \nonumber \]

або обидва сходяться, або обидва розходяться

p -серія

серія форми\(\displaystyle \sum^∞_{n=1}1/n^p\)

залишок кошторис

для ряду\(\displaystyle \sum^∞_{n=}1a_n\) з додатними членами\( a_n\) та неперервною спадною функцією, що\( f(n)=a_n\) для всіх натуральних чисел\( n\) залишок\(\displaystyle R_N=\sum^∞_{n=1}a_n−\sum^N_{n=1}a_n\) задовольняє\( f\) такій оцінці:

\[∫^∞_{N+1}f(x)\,dx<R_N<∫^∞_Nf(x)\,dx \nonumber \]