7.1: Площа між кривими

Last updated
Save as PDF

Page ID: 60707

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Ми починаємо цю главу з нагадування про кілька ключових понять з глави 5. $f$Дозволяти неперервна функція$[a,b]$, на якій розбито на$n$ підінтервали як

$a<x_1 < x_2 <\ cdots < x_n<x_ {n+1} =б.\]

$dx_i$Дозволяти позначають довжину$i^\text{ th}$ підінтервалу, і нехай$c_i$ бути будь-яке$x$ -значення в цьому підінтервалі. Визначення 5.3.1 стверджує, що сума

$\ сума_ {i=1} ^n f (c_i)\ dx_i\]

це сума Рімана. Суми Рімана часто використовуються для наближення деякої величини (площа, обсяг, робота, тиск і т.д.). Наближення стає точним, приймаючи межу

$\ lim_ {||dx_i||\ до0}\ сума {i=1} ^n f (c_i)\ dx_i,\]

де$||\ dx_i||$ довжина найбільшого субінтервалу в перегородці. Теорема 5.3.2 пов'язує межі сум Рімана з певними інтегралами:

$\ lim_ {||dx_i||\ до0}\ сума_ {i=1} ^n f (c_i)\ dx_i =\ int_a^b f (x)\ дх.\]

Нарешті, Фундаментальна теорема обчислення стверджує, як визначені інтеграли можна оцінити за допомогою антипохідних.

У цьому розділі використовується наступна техніка для різних застосувань. Припустимо$Q$, значення величини підлягає обчислення. Спочатку ми наближаємо значення$Q$ використання суми Рімана, потім знаходимо точне значення через певний інтеграл. Ми викладемо цю техніку в наступній ключовій ідеї.

Ключова ідея 22: Певна інтегральна стратегія

Нехай задано величину, значення$Q$ якої слід обчислити.

Розділіть кількість на$n$ менші «підвеличини» значення$Q_i$.
Визначте змінну$x$ та функцію,$f(x)$ таку, що кожна підкількість може бути апроксимована з добутком$f(c_i)\ dx_i$, де$dx_i$ представляє невелику зміну$x$. Таким чином$Q_i \approx f(c_i)\ dx_i$. Зразок$f(c_i)\ dx_i$ наближення$Q_i$ називається диференціальним елементом.
Визнайте$ Q= \sum_{i=1}^n Q_i \approx \sum_{i=1}^n f(c_i)\ dx_i$, що це сума Рімана.
Прийняття відповідного ліміту дає$ Q = \int_a^b f(x)\ dx$

Ця ключова ідея матиме більше сенсу після того, як ми мали можливість використати її кілька разів. Почнемо з площі між кривими, яку ми коротко розглянули в розділі 5.5.4.

Площа між кривими

Ми часто зацікавлені в тому, щоб знати область регіону. Забудьте на мить, що ми розглянули це вже в розділі 5.5.4, і натомість підійдіть до нього, використовуючи техніку, описану в Key Idea 22.

$Q$Дозволяти площа області, обмеженої неперервними функціями$f$ і$g$. Якщо ми розбиваємо область на багато субрегіонів, то маємо очевидне рівняння:

\[\text{Total Area} = \text{sum of the areas of the subregions.}\]

Питання, яке слід вирішити, полягає в тому, як систематично розбивати регіон на субрегіони. Допоможе графік. Розглянемо Малюнок,$\PageIndex{1a}$ де область між двома кривими затінена. Хоча існує багато способів розбити це на субрегіони, одним з особливо ефективних способів є «розрізати» його вертикально, як показано на малюнку$\PageIndex{1b}$, на$n$ однаково розташовані фрагменти.

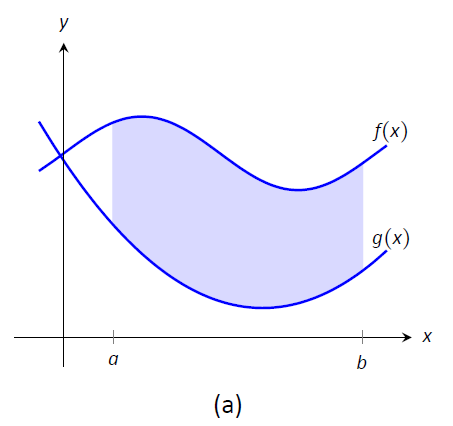
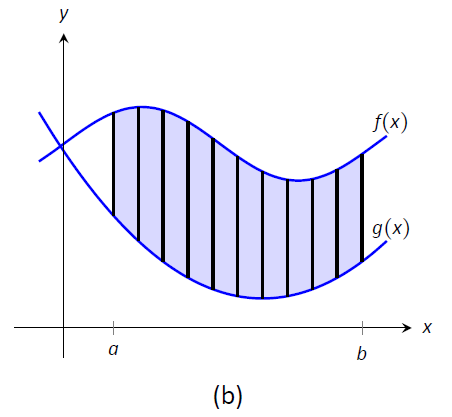
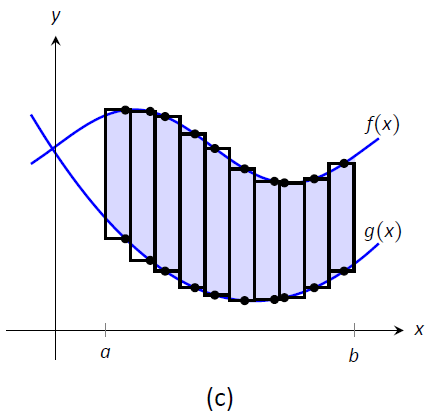
$7.1.1a.png$ $7.1.1 б.пнг$ $7.1.1 к.пнг$

Малюнок$\PageIndex{1}$: Розділення області на вертикальні зрізи та апроксимування ділянок прямокутниками.

Тепер ми наближаємо площу зрізу. Знову ж таки, у нас є багато варіантів, але використання прямокутника здається найпростішим. Підібравши будь-яке$x$ -значення$c_i$ в$i^\text{ th}$ зрізі, встановлюємо висоту прямокутника бути$f(c_i)-g(c_i)$, різниця відповідних$y$ -значень. Ширина прямокутника - це невелика різниця в$x$ -значеннях, які ми представляємо з$dx$. $\PageIndex{1c}$На малюнку показані вибіркові точки,$c_i$ вибрані в кожному підінтервалі, і відповідні прямокутники, на (Кожен з цих прямокутників являє собою диференціальний елемент.) Кожен зріз має площу, приблизно рівну$\big(f(c_i)-g(c_i)\big)\ dx$; отже, загальна площа приблизно дорівнює сумі Рімана

$ $ Q =\ сума_ {i = 1} ^n\ великий (f (c_i) -г (c_i)\ великий)\ dx.\]

Беручи межу, оскільки$n\to \infty$ дає точну площу, як$\int_a^b \big(f(x)-g(x)\big)\ dx.$

Теорема$\PageIndex{1}$: Area Between Curves

$g(x)$Дозволяти$f(x)$ і бути безперервні функції, визначені на$[a,b]$ де$f(x)\geq g(x)$ для всіх$x$ в$[a,b]$. Площа області обмежена кривими$y=f(x)$,$y=g(x)$ а лініями$x=a$ і$x=b$ є

$\ int_a^b\ великий (f (x) -г (х)\ великий)\ dx.\]

Приклад$\PageIndex{1}$: Finding area enclosed by curves

Знайдіть площу області, обмеженої$f(x) = \sin x+2$,$x=0$ і$g(x) = \dfrac12\cos (2x)-1$$x=4\pi$, як показано на малюнку$\PageIndex{2}$.

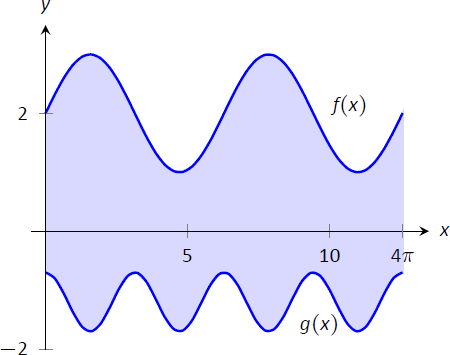
$imageedit_2_9982172939.png$

Малюнок$\PageIndex{2}$: Графік замкненої області в прикладі$\PageIndex{1}$.

Рішення

Графік перевіряє, що верхня межа області задана,$f$ а нижня межа задана$g$. Тому площа області є значенням інтеграла

\[\begin{align*}\int_0^{4\pi} \big(f(x)- g(x)\big)\ dx & = \int_0^{4\pi} \Big(\sin x+2 - \big(\dfrac12\cos (2x)-1\big)\Big)\ dx \\[4pt]&= -\cos x -\dfrac14\sin(2x)+3x\Big|_0^{4\pi}\\[4pt] &= 12\pi \approx 37.7\ \text{units}^2.\end{align*}\]

Приклад$\PageIndex{2}$: Finding total area enclosed by curves

Знайдіть загальну площу області, укладеної функціями$f(x) = -2x+5$ і$g(x) = x^3-7x^2+12x-3$ як показано на малюнку$\PageIndex{3}$.

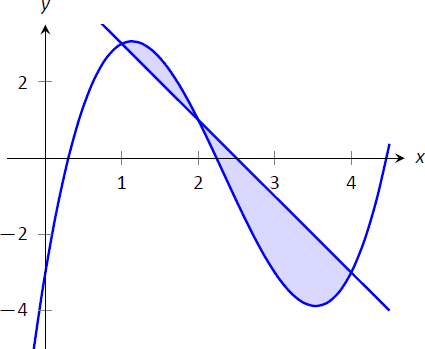
$imageedit_6_8824349634.png$

Рисунок$\PageIndex{3}$: Графік області, укладеної двома функціями у прикладі$\PageIndex{2}$.

Рішення

Швидкий розрахунок показує, що$f=g$ в$x=1, 2$ і 4. Можна бездумно вчинити за допомогою обчислень$ \int_1^4\big(f(x)-g(x)\big)\ dx$, але це ігнорує той факт, що на$[1,2]$,$g(x)>f(x)$. (Насправді, бездумна інтеграція повертається$-9/4$, навряд чи очікувана вартість області.) Таким чином, ми обчислюємо загальну площу, розбиваючи інтервал$[1,4]$ на два підінтервали,$[1,2]$$[2,4]$ і використовуючи власне integrand в кожному.

\[\begin{align*} \text{Total Area} &= \int_1^2 \big(g(x)-f(x)\big)\ dx + \int_2^4\big(f(x)-g(x)\big)\ dx\\[4pt] &= \int_1^2 \big(x^3-7x^2+14x-8\big) \ dx + \int_2^4\big(-x^3+7x^2-14x+8\big)\ dx\\[4pt] &= 5/12 + 8/3 \\[4pt] &= 37/12 = 3.083\ \text{units}^2.\end{align*} \]

У попередньому прикладі зазначається, що ми очікуємо, що область буде позитивною. Коли вперше дізнавшись про певний інтеграл, ми інтерпретували його як «підписану область під кривою», що дозволяє «негативну область». Це не застосовується тут; область повинна бути позитивною.

Попередній приклад також демонструє, що нам часто доводиться розбивати задану область на субрегіони перед застосуванням теореми$\PageIndex{1}$. Наступний приклад показує іншу ситуацію, коли це може бути застосовано, а також альтернативний погляд на застосування теореми.

Приклад$\PageIndex{3}$: Finding area: integrating with respect to $y$

Знайдіть площу області, укладеної функціями$y=\sqrt{x}+2$,$y=-(x-1)^2+3$ і$y=2$, як показано на малюнку$\PageIndex{4}$.

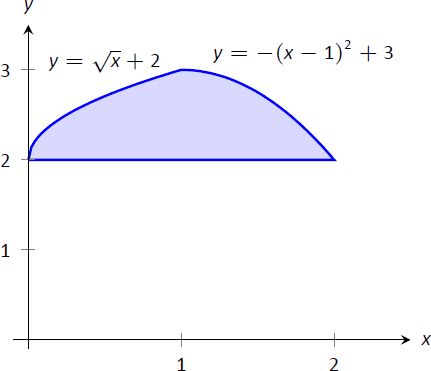
$imageedit_10_2062732782.png$

Малюнок$\PageIndex{4}$: Графік області для Приклад$\PageIndex{3}$.

Рішення

Наведемо два підходи до цієї проблеми. У першому підході ми помічаємо, що «вершина» регіону визначається двома різними кривими. На$[0,1]$, верхня функція є$y=\sqrt{x}+2$; на$[1,2]$, верхня функція є$y=-(x-1)^2+3$.

Таким чином обчислюємо площу як суму двох інтегралів:

\[\begin{align*} \text{Total Area} &= \int_0^1 \Big(\big(\sqrt{x}+2\big)-2\Big)\ dx + \int_1^2 \Big(\big(-(x-1)^2+3\big)-2\Big)\ dx \\[4pt] &= 2/3 + 2/3\\[4pt] &=4/3.\end{align*}\]

Другий підхід розумний і дуже корисний в певних ситуаціях. Ми звикли переглядати криві як функції$x$; ми вводимо$x$ значення -value і повертається$y$ -value. Деякі криві також можуть бути описані як функції$y$: input a$y$ -value і$x$ -value повертається. Ми можемо переписати рівняння, що описують межу, вирішивши для$x$:

$ $ y=\ sqrt {x} +2\ квад\ Стрілка вправо\ квад x = (y-2) ^2\]

$ $ y=- (x-1) ^2+3\ квад\ Стрілка вправо\ квад x =\ sqrt {3-y} +1.\]

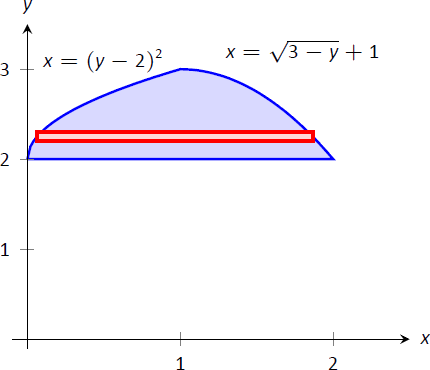
$imageedit_14_3135847777.png$

Малюнок$\PageIndex{5}$: Область, що використовується в Прикладі$\PageIndex{3}$ з межами, позначеними як функції$y$.

$\PageIndex{5}$На малюнку показана область з маркуванням меж. Також зображений диференціальний елемент, горизонтальний прямокутник. Ширина прямокутника - це невелика зміна в$y$:$\Delta y$. Висота прямокутника - це різниця в$x$ -значеннях. «top»$x$ -value є найбільшим значенням, тобто крайнім правим. $x$Значення «знизу» - менше, тобто крайнє ліве. Тому висота прямокутника дорівнює

$\ великий (\ sqrt {3-й} +1\ великий) - (y-2) ^2.\]

Площа знаходить шляхом інтеграції вищевказаної функції$y$ щодо відповідних меж. Визначаємо їх, враховуючи$y$ -значення, які займає регіон. Він обмежений нижче$y=2$, і обмежений вище$y=3$. Тобто і функції «верх», і «низ» існують на$y$ проміжку$[2,3]$. Таким чином

\[\begin{align*}\text{Total Area} &= \int_2^3 \big(\sqrt{3-y}+1 - (y-2)^2\big)\ dy \\[4pt] &= \Big(-\dfrac23(3-y)^{3/2}+y-\dfrac13(y-2)^3\Big)\Big|_2^3 \\[4pt] &= 4/3.\end{align*}\]

Ця методика пошуку області на основі обчислень може бути корисною навіть з формами, які ми зазвичай вважаємо «легкими». Приклад$\PageIndex{4}$ обчислює площу трикутника. Хоча формула "$\dfrac12\times\text{base}\times\text{height}$" добре відома, в довільних трикутниках можна нетривіально обчислити висоту. Обчислення робить задачу простою.

Приклад$\PageIndex{4}$: Finding the area of a triangle

Обчислити площу областей, обмежених лініями

$y=x+1$,$y=-2x+7$ І$y=-\dfrac12x+\dfrac52$, як показано на рис$\PageIndex{6}$.

$imageedit_18_4655953817.png$

Малюнок$\PageIndex{6}$: Графік трикутної області на прикладі$\PageIndex{4}$

Рішення

Визнайте, що в цій області є дві «верхні» функції, що змушує нас використовувати два певні інтеграли.

\[\begin{align*}\text{Total Area} &= \int_1^2\big((x+1)-(-\dfrac12x+\dfrac52)\big)\ dx + \int_2^3\big((-2x+7)-(-\dfrac12x+\dfrac52)\big)\ dx \\[4pt] &= 3/4+3/4\\[4pt] &=3/2.\end{align*}\]

Ми також можемо підійти до цього шляхом перетворення кожної функції в функцію$y$. Для цього також потрібні інтеграли 2, тому немає жодної переваги для цього. Ми робимо це тут для демонстраційних цілей.

Функція «зверху» завжди,$x=\dfrac{7-y}2$ поки є дві «нижні» функції. Пам'ятаючи про належні межі інтеграції, ми маємо

\[\begin{align*} \text{Total Area} &= \int_1^2\big(\dfrac{7-y}2 - (5-2y)\big)\ dy + \int_2^3\big(\dfrac{7-y}2-(y-1)\big)\ dy \\[4pt] &= 3/4 + 3/4\\[4pt] &= 3/2.\end{align*}\]

Звичайно, остаточна відповідь той же. (Цікаво відзначити, що площа всіх 4 використовуваних субрегіонів становить 3/4. Це випадково.)

Хоча ми зосередилися на отриманні точних відповідей, ми також можемо робити наближення, використовуючи принцип теореми$\PageIndex{1}$. Інтегран в теоремі - це відстань («верх мінус низ»); інтеграція цієї функції відстані дає площу. Здійснюючи дискретні вимірювання відстані, ми можемо наблизити площу за допомогою методів числового інтегрування, розроблених у розділі\ ref {sec:numerical_integration}. Наступний приклад демонструє це.

Приклад$\PageIndex{5}$: Numerically approximating area

Щоб наблизити площу озера, показану на малюнку$\PageIndex{7a}$, «довжина» озера вимірюється з кроком 200 футів, як показано на малюнку$\PageIndex{7b}$, де довжини наведені в сотнях футів. Приблизна площа озера.

Рішення

Вимірювання довжини можна розглядати як вимірювання «верх мінус низ» двох функцій. Точну відповідь можна знайти шляхом інтеграції$\int_0^{12} \big(f(x)-g(x)\big)\ dx$, але, звичайно, ми не знаємо функцій$f$ і$g$. Наші дискретні вимірювання замість цього дозволяють нам наблизити.

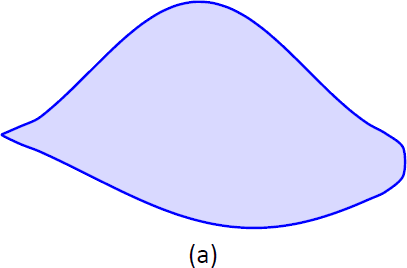
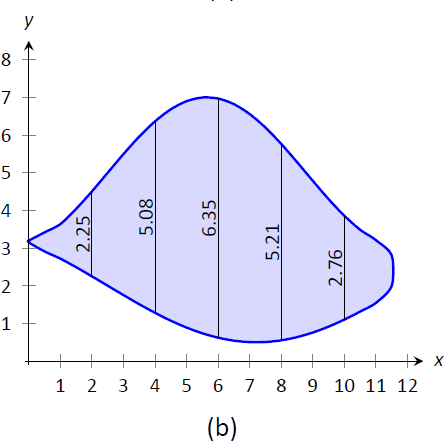
$imageedit_22_5823047485.png$ $imageedit_26_8042194042.png$

Малюнок$\PageIndex{7}$: (а) ескіз озера, і (б) озера з вимірами довжини.

У нас є такі дані:

$ (0,0),\ (2,2.25),\ (4,5.08),\ (6,6.35),\ (8,5.21),\ (10,2.76),\ (12,0).\]

Ми також маємо це$dx=\dfrac{b-a}{n} = 2$, тому Правило Сімпсона дає

\[\begin{align*}\text{Area}&\approx \dfrac{2}{3}\Big(1\cdot0+4\cdot2.25+2\cdot5.08+4\cdot6.35+2\cdot5.21+4\cdot2.76+1\cdot0\Big)\\[4pt] &= 44.01\overline{3} \ \text{units}^2.\end{align*}\]

Оскільки вимірювання знаходяться в сотнях футів, одиниць$^2 = (100\ \text{ft})^2 = 10,000\ \text{ft}^2$, що дають загальну площу$440,133\ \text{ft}^2$. (Оскільки ми наближаємося, ми, швидше за все, скажемо$440,000\ \text{ft}^2$, площа була приблизно, що трохи більше 10 акрів.)

У наступному розділі ми застосовуємо наші методи інтеграції додатків для пошуку обсягів певних твердих речовин.