6.7: Правило L'Hopital

Last updated
Save as PDF

Page ID: 60779

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Хоча ця глава присвячена вивченню методів інтеграції, цей розділ не стосується інтеграції. Швидше, це стосується техніки оцінки певних меж, яка буде корисна в наступному розділі, де інтеграція ще раз обговорюється.

Наше лікування меж піддало нас «0/0», невизначеній формі. Якщо$ \lim_{x\to c}f(x)=0$ і$ \lim_{x\to c} g(x) =0$, ми не робимо висновок, що$ \lim_{x\to c} f(x)/g(x)$ є$0/0$; скоріше, ми використовуємо$0/0$ як позначення для опису того факту, що і чисельник, і знаменник наближаються до 0. Вираз 0/0 не має числового значення; для обчислення межі потрібно виконати іншу роботу.

Існують і інші невизначені форми; ними є:$\infty/\infty$$0\cdot\infty$,,$\infty-\infty$,$0^0$,$1^\infty$ і$\infty^0$. Так само, як «0/0" не означає «розділити 0 на 0», вираз "$\infty/\infty$" не означає «розділити нескінченність на нескінченність». Натомість це означає «кількість зростає без зв'язків і ділиться на іншу величину, яка зростає без зв'язків». Ми не можемо визначити з такого твердження, яке значення, якщо воно є, призводить до ліміту. Аналогічно, "$0\cdot \infty$" не означає «помножити нуль на нескінченність». Натомість це означає, що «одна кількість скорочується до нуля і множиться на величину, яка зростає без обмежень». З такого опису ми не можемо визначити, яким буде результат такого ліміту.

У цьому розділі представлено правило L'Hôpital, метод вирішення обмежень, які створюють невизначені форми 0/0 і$\infty/\infty$. Ми також покажемо, як алгебраїчні маніпуляції можуть бути використані для перетворення інших невизначених виразів в одну з цих двох форм, щоб можна було застосувати наше нове правило.

Теорема$\PageIndex{1}$: L'Hôpital's Rule

Нехай$\lim_{x\to c}f(x) = 0$ і$\lim_{x\to c}g(x)=0$, де$f$ і$g$ диференційовні функції на відкритому інтервалі$I$ містять$c$, і$g'(x)\neq 0$ на$I$ крім можливо в$c$. Тоді

$\ lim_ {x\ to c}\ frac {f (x)} {g (x)} =\ lim_ {x\ to c}\ frac {f' (x)} {g' (x)}.\]

Ми демонструємо використання правила L'Hôpital в наступних прикладах; ми часто будемо використовувати «LHR» як абревіатуру «L'Hôpital»

Приклад$\PageIndex{1}$: Using L'Hôpital's Rule

Оцініть наступні обмеження, використовуючи Правило L'Hôpital в міру необхідності.

$ \lim_{x\to0}\frac{\sin x}x$
$ \lim_{x\to 1}\frac{\sqrt{x+3}-2}{1-x}$
$ \lim_{x\to0}\frac{x^2}{1-\cos x}$
$ \lim_{x\to 2}\frac{x^2+x-6}{x^2-3x+2}$

Рішення

Ми довели, що ця межа дорівнює 1 у прикладі\ ref {ex_limit_sinx_prove} за допомогою теореми стискання. Тут ми використовуємо правило L'Hôpital, щоб показати свою силу. $\ lim_ {x\ to0}\ frac {\ sin x} х\ stackrel {\ текст {по LHR}\} {=}\ lim_ {x\ to0}\ frac {\ cos x} {1} =1. $$
$ \lim_{x\to 1}\frac{\sqrt{x+3}-2}{1-x} \stackrel{\ \text{ by LHR } \ }{=} \lim_{x \to 1} \frac{\frac12(x+3)^{-1/2}}{-1} =-\frac 14.$
$ \lim_{x\to 0}\frac{x^2}{1-\cos x} \stackrel{ \text{ by LHR } }{=} \lim_{x\to 0} \frac{2x}{\sin x}.$
Ця остання межа також оцінюється до невизначеної форми 0/0. Щоб оцінити його, ми знову застосуємо Правило L'Hôpital. $\ lim_ {x\ to 0}\ frac {2x} {\ sin x}\ stackrel {\ text {по LHR}} {=}\ frac {2} {\ cos x} = 2 .$$ Таким чином$ \lim_{x\to0}\frac{x^2}{1-\cos x}=2.$
Ми вже знаємо, як оцінити цю межу; перший множник чисельник і знаменник. Потім ми маємо: $\ lim_ {x\ to 2}\ frac {x^2+x-6} {x^2-3x+2} =\ lim_ {x\ to 2}\ frac {(x-2) (x-3)} {x-2) (x-1)} =\ lim_ {x\ до 2}\ frac {x+3} {x-1} = 5.$Ми тепер показати, як вирішити це, використовуючи правило L'Hôpital. $\ lim_ {х\ до 2}\ розрив {x^2+x-6} {x^2-3x+2}\ stackrel {\ текст {по LHR}} {=}\ lim_ {x\ to 2}\ frac {2x+1} {2x-3} = 5. $$

Зверніть увагу, що на кожному кроці, де було застосовано правило L'Hôpital, це було потрібно: початкова межа повертала невизначену форму "»$0/0$. Якщо початковий ліміт повертається, наприклад, 1/2, то правило L'Hôpital не застосовується.

Наступна теорема розширює нашу початкову версію правила L'Hôpital двома способами. Це дозволяє застосовувати техніку до невизначеної форми$\infty/\infty$ та до меж, де$x$ наближається$\pm\infty$.

Теорема$\PageIndex{2}$: L'Hôpital's Rule, Part 2

Нехай$\lim_{x\to a}f(x) = \pm\infty$ і$\lim_{x\to a}g(x)=\pm \infty$, де$f$ і$g$ диференційовані на відкритому інтервалі,$I$ що містять$a$. Потім $\ lim_ {x\ to a}\ frac {f (x)} {g (x)} =\ lim_ {x\ to a}\ frac {f' (x)} {g' (x)} . $$
$g$Дозволяти$f$ і бути диференційовні функції на відкритому інтервалі$(a,\infty)$ для$a$ деякого значення, де$g'(x)\neq 0$ on$(a,\infty)$ і$\lim_{x\to\infty} f(x)/g(x)$ повертає або 0/0 або$\infty/\infty$. Тоді $$\ lim_ {x\ to\ infty}\ frac {f (x)} {g (x)} =\ lim_ {x\ to\ infty}\ frac {f' (x)} {g' (x)} .$$ Аналогічний оператор може бути зроблений для обмежень, де$x$ наближається$-\infty$.

Приклад$\PageIndex{2}$: L'Hôpital's Rule with limits involving $\infty$

Оцініть наступні межі.

$1.\\ lim_ {x\ to\ infty}\ розрив {3x^2-100x+2} {4x^2+5x-1000}\ qquad\ qquad 2.\\ lim_ {x\ to\ intty}\ frac {e^x} {x^3}.\]

Рішення

Ми можемо оцінити цю межу вже за допомогою теореми\ ref {thm:lim_rational_fn_at_infty}; відповідь 3/4. Ми застосовуємо правило L'Hôpital, щоб продемонструвати його застосовність. $\ lim_ {x\ to\ infty}\ frac {3x^2-100x+2} {4x^2+5x-1000}\ штабелер {\\ текст {по LHR}\} {=}\ lim_ {x\ to\ inty}\ frac {6x-100} {8x+5}\ стекер {\ текст {LHR}\}\ lim_ {х\ до\ infty}\ фрак68 =\ фрак34. $$
$\ lim_ {x\ to\ infty}\ frac {e^x} {x^3}\ стекерл {\\ текст {по LHR}\} {=}\ lim_ {x\ inty}\ frac {e^x} {3x^2}\ stackrel {\\ текст {по LHR}\} {=}\ lim_ {x\ до\ infty}\ frac {e^x} {6x}\ stackrel {\\ text {по LHR}\} {=}\ lim_ {x\ to\ infty}\ frac {e^x} {6} =\ infty.$$ Нагадаємо, що це означає, що обмеження не існує; як $x$наближається$\infty$, вираз$e^x/x^3$ зростає без прив'язки. З цього можна зробити висновок, що$e^x$ росте «швидше», ніж$x^3$; як$x$ стає великим,$e^x$ набагато більше, ніж$x^3$. (Це має важливі наслідки для обчислень при розгляді ефективності алгоритмів.)

Правило L'Hôpital може застосовуватися лише до співвідношень функцій. Зіткнувшись з невизначеною формою, такою як$0\cdot\infty$ або$\infty-\infty$, ми іноді можемо застосувати алгебру, щоб переписати межу, щоб можна було застосувати правило L'Hôpital. Продемонструємо загальну ідею в наступному прикладі.

Приклад$\PageIndex{3}$: Applying L'Hôpital's Rule to other indeterminate forms

Оцініть наступні межі.

$ \lim_{x\to0^+} x\cdot e^{1/x}$
$ \lim_{x\to0^-} x\cdot e^{1/x}$
$ \lim_{x\to\infty} \ln(x+1)-\ln x$
$ \lim_{x\to\infty} x^2-e^x$

Рішення

Як$x\rightarrow 0^+$,$x\rightarrow 0$ і$e^{1/x}\rightarrow \infty$. Таким чином, ми маємо невизначену форму$0\cdot\infty$. Ми переписуємо вираз$x\cdot e^{1/x}$ як$\frac{e^{1/x}}{1/x}$; тепер$x\rightarrow 0^+$, як, ми отримуємо невизначену форму,$\infty/\infty$ до якої можна застосувати правило L'Hôpital. $$\ lim_ {x\ to0^+} x\ cdot e^ {1/x} =\ lim_ {x\ to 0^+}\ frac {e^ {1/x}} {1/x}\ stackrel {\\ text {LHR}\} {=}\ lim_ {х\ до 0^+}\ розрив {(-1/x^2) e^ {1/x}} {-1/x^2} =\ lim_ {x\ to 0^+} e^ {1/x} =\ infty.$$ Інтерпретація:$e^{1/x}$ зростає «швидше», ніж$x$ стискається до нуля, тобто їхній продукт росте без зв'язків.
Як$x\rightarrow 0^-$,$x\rightarrow 0$ і$e^{1/x}\rightarrow e^{-\infty}\rightarrow 0$. Межа оцінює$0\cdot 0$, до якої не є невизначеною формою. Зробимо висновок, що $$\ lim_ {x\ to 0^-} x\ cdot e^ {1/x} = 0.\]
Ця межа спочатку оцінюється до невизначеної форми$\infty-\infty$. Застосовуючи логарифмічне правило, ми можемо переписати межу як
$$\ lim_ {x\ to\ infty}\ ln (x+1) -\ ln x =\ lim_ {x\ to\ infty}\ ln\ left (\ frac {x+1} x\ right) .$$ Як$x\rightarrow \infty$, аргумент$\ln$ терміна підходить$\infty/\infty$, до якого ми можемо застосувати Правило L'Hôpital. $$\ lim_ {x\ to\ infty}\ frac {x+1} x\ stackrel {\\ текст {по LHR}\} {=}\ frac11=1.$$ З$x\rightarrow \infty$ випливає$\frac{x+1}x\rightarrow 1$, що $$x\ rightarrow\ infty\ quad\ text {має на увазі}\ quad\ ln\ ліворуч (\ frac {x+1} х\ вправо)\ стрілка вправо\ n 1n =0.\]
Таким чином $$\ lim_ {x\ to\ infty}\ ln (x+1) -\ ln x =\ lim_ {x\ to\ infty}\ ln\ left (\ frac {x+1} x\ right) =0.$$ Інтерпретація: оскільки ця межа оцінюється в 0, то це означає$x$, що для великих різниці між$\ln (x+1)$ і по суті немає$\ln x$; їх різниця по суті дорівнює 0.
Ліміт$ \lim_{x\to\infty} x^2-e^x$ спочатку повертає невизначену форму$\infty-\infty$. Ми можемо переписати вираз факторингом$x^2$;$ x^2-e^x = x^2\left(1-\frac{e^x}{x^2}\right).$ Нам потрібно оцінити, як$e^x/x^2$ поводиться як$x\rightarrow \infty$: $\ lim_ {x\ to\ infty}\ frac {x^x} {x^2}\ stackrel {\\ text {по LHR}\} {=}\ lim_ {x\ to\ infty}\ frac {e^x} {2x}\ stackrel {текст {по LHR}\} {=}\ lim_ {x\ to\ infty}\ frac {e^x} {2} =\ infty.\]
Таким чином$\lim_{x\to\infty}x^2(1-e^x/x^2)$ оцінює до$\infty\cdot(-\infty)$, що не є невизначеною формою; скоріше,$\infty\cdot(-\infty)$ оцінює до$-\infty$. Ми робимо висновок, що$ \lim_{x\to\infty} x^2-e^x = -\infty.$

Тлумачення: як$x$ стає великим, різниця між$x^2$ і$e^x$ зростає дуже велика.

Індетермінантні форми$0^0$,$1^\infty$ і$\infty^0$

Зіткнувшись з невизначеною формою, яка передбачає владу, вона часто допомагає використовувати природну логарифмічну функцію. Наступна Key Idea висловлює концепцію, за якою слідує приклад, який демонструє її використання.

Ключова ідея 20: Оцінка меж за участю невизначені форми$0^0$, $1^\infty$ and $\infty^0$

Якщо$ \lim_{x\to c} \ln\big(f(x)\big) = L$, то$ \lim_{x\to c} f(x) = \lim_{x\to c} e^{\ln(f(x))} = e\,^L.$

Приклад$\PageIndex{4}$: Using L'Hôpital's Rule with indeterminate forms involving exponents

Оцініть наступні межі.

$ 1. \lim_{x\to\infty} \left(1+\frac1x\right)^x \qquad\qquad 2. \lim_{x\to0^+} x^x.$

Рішення

Це еквівалентно спеціальній межі, наведеній у теоремі\ ref {thm:lim_continuous}; ці межі мають важливе застосування в математиці та фінансах. Зверніть увагу, що показник наближається,$\infty$ тоді як база наближається до 1, що призводить до невизначеної форми$1^\infty$. Нехай$f(x) = (1+1/x)^x$; проблема просить оцінити$\lim_{x\to\infty}f(x)$. Давайте спочатку оцінимо$ \lim_{x\to\infty}\ln\big(f(x)\big)$. \[\begin{align}\lim_{x\to\infty}\ln\big(f(x)\big) & = \lim_{x\to\infty} \ln \left(1+\frac1x\right)^x \\ &= \lim_{x\to\infty} x\ln\left(1+\frac1x\right)\\ &= \lim_{x\to\infty} \frac{\ln\left(1+\frac1x\right)}{1/x}\end{align}\]Це створює невизначену форму 0/0, тому ми застосовуємо правило L'Hôpital. \[\begin{align}&= \lim_{x\to\infty} \frac{\frac{1}{1+1/x}\cdot(-1/x^2)}{(-1/x^2)} \\&= \lim_{x\to\infty}\frac{1}{1+1/x}\\ &= 1. \end{align}\]Таким чином$\lim_{x\to\infty} \ln \big(f(x)\big) = 1.$ повертаємося до початкового межі і застосовуємо Key Idea 20. $\ lim_ {x\ to\ infty}\ ліворуч (1+\ frac1x\ праворуч) ^x =\ lim_ {x\ to\ infty} f (x) =\ lim_ {x\ to\ infty} e^ {\ ln (f (x))} = e^1 = e.\]
Ця межа призводить до невизначеної формі$0^0$. Давайте$f(x) = x^x$ і розглянемо спочатку$\lim_{x\to0^+} \ln\big(f(x)\big)$. \[\begin{align} \lim_{x\to0^+} \ln\big(f(x)\big) &= \lim_{x\to0^+} \ln\left(x^x\right) \\ &= \lim_{x\to0^+} x\ln x \\ &= \lim_{x\to0^+} \frac{\ln x}{1/x}.\end{align}\]Це створює невизначену форму,$-\infty/\infty$ тому ми застосовуємо правило L'Hôpital. \[\begin{align} &= \lim_{x\to0^+} \frac{1/x}{-1/x^2} \\ &= \lim_{x\to0^+} -x \\ &= 0. \end{align}\]Таким чином$\lim_{x\to0^+} \ln\big(f(x)\big) =0$. Повертаємося до початкового ліміту і застосовуємо Key Idea 20. $\ lim_ {x\ to0^+} x^x =\ lim_ {x\ to0^+} f (x) =\ lim_ {x\ to0^+} e^ {\ ln (f (x))} = e^0 = 1.$$ Цей результат підтримується графіком,$f(x)=x^x$ наведеним на малюнку$\PageIndex{1}$.

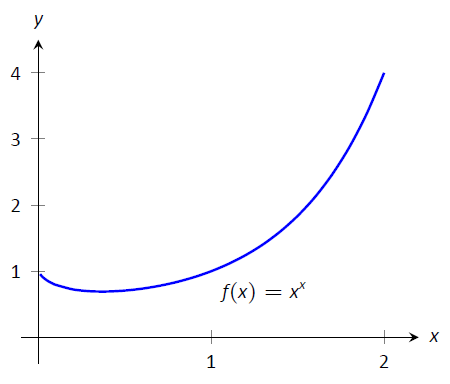
$6.7.1.png$

Малюнок$\PageIndex{1}$: Графік$f(x)=x^x$ підтвердження того, що як$x\to 0^+$,$f(x)\to 1$.

Наш короткий перегляд лімітів буде винагороджений у наступному розділі, де ми вважаємо неправильну інтеграцію. Поки що ми розглядали лише певні інтеграли, де межею є кінцеві числа, такі як$\int_0^1 f(x)\ dx$. Неправильне інтегрування розглядає інтеграли, де одна або обидві межі є «нескінченністю». Такі інтеграли мають багато застосувань та застосувань, крім генерування ідей, які є просвітницькими.