6.8: Неправильна інтеграція

Last updated
Save as PDF

Page ID: 60821

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Ми починаємо цей розділ з розгляду наступних визначених інтегралів:

\[ \int_0^{100}\dfrac1{1+x^2}\ dx \approx 1.5608,\]

\[ \int_0^{1000}\dfrac1{1+x^2}\ dx \approx 1.5698,\]

\[ \int_0^{10,000}\dfrac1{1+x^2}\ dx \approx 1.5707.\]

Зверніть увагу, як integrand знаходиться$1/(1+x^2)$ в кожному інтегралі (який намальований на малюнку$\PageIndex{1}$). Оскільки верхня межа стає більшою, можна було б очікувати, що «площа під кривою» також зросте. Хоча певні інтеграли збільшуються у значенні у міру зростання верхньої межі, вони не збільшуються значно. По суті, розглянемо:

$\ begin {вирівнювання}\ int_0^b\ frac {1} {1+x^2}\ dx &=\ ліворуч. \ tan^ {-1} х\ право|_0^b\\[4pt] &= \tan^{-1}b-\tan^{-1}0 \\[4pt] &= \tan^{-1}b. \end{align}\]

Як$b\rightarrow \infty$,$\tan^{-1}b \rightarrow \pi/2.$ Тому здається, що у$b$ міру зростання верхньої межі значення певного інтеграла$\int_0^b\frac{1}{1+x^2}\ dx$ наближається$\pi/2\approx 1.5708$. Це повинно вразити читача як трохи дивовижне: незважаючи на те, що крива поширюється «до нескінченності», вона має кінцеву кількість площі під нею.

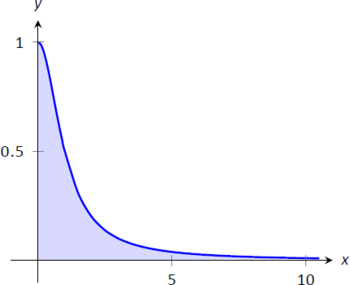
$imageedit_2_3685343619.png$

Малюнок$\PageIndex{1}$: Графік$ f(x)=\frac{1}{1+x^2}$

Коли ми визначили певний інтеграл$\int_a^b f(x)\ dx$, ми зробили два умови:

Інтервал, над яким ми інтегрували$[a,b]$, був кінцевим інтервалом, і
Функція$f(x)$ була безперервною$[a,b]$ (гарантуючи, що діапазон$f$ був кінцевим).

У цьому розділі розглядаються інтеграли, де одна або обидві з перерахованих вище умов не витримуються. Такі інтеграли називаються невідповідними інтегралами.

Неправильні інтеграли з нескінченними межами

Визначення$\PageIndex{1}$: Improper Integrals with Infinite Bounds; Converge, Diverge

$f$Дозволяти бути безперервної функції на$[a,\infty)$. Визначте $\ int_a^\ infty f (x)\ dx\ equiv\ lim_ {b\ to\ infty}\ int_a^b f (x)\ dx. $$
$f$Дозволяти бути безперервної функції на$(-\infty,b]$. Визначте $\ int_ {-\ infty} ^b f (x)\ dx\ equiv\ lim_ {a\ to-\ infty}\ int_a^b f (x)\ dx. $$
$f$Дозволяти бути безперервної функції на$(-\infty,\infty)$. Дозволяти$c$ бути будь-яке дійсне число; визначити $\ int_ {-\ infty} ^\ infty f (x)\ dx\ equiv\ lim_ {a\ to-\ infty}\ int_a^c f (x)\ dx\ +\ lim_ {b\ to\ infty}\ int_c^b f (x)\ dx. $$

Неправильний інтеграл, як кажуть, сходиться, якщо існує відповідна межа; в іншому випадку він розходиться. Неправильний інтеграл в частині 3 сходиться тоді і тільки тоді, коли існують обидві його межі.

Приклад$\PageIndex{1}$: Evaluating improper integrals

Оцініть наступні неправильні інтеграли.

$\int_1^\infty \frac1{x^2}\ dx$
$\int_1^\infty \frac1x\ dx$
$\int_{-\infty}^0 e^x\ dx$
$\int_{-\infty}^\infty \frac1{1+x^2}\ dx$

Рішення

\[\begin{align}[t] \int_1^\infty \frac{1}{x^2}\ dx\ =\ \lim_{b\to\infty} \int_1^b\frac1{x^2}\ dx\ &=\ \lim_{b\to\infty} \frac{-1}{x}\Big|_1^b \\ &= \lim_{b\to\infty} \frac{-1}{b} + 1\\ &= 1.\end{align}\]Графік площі, визначеної цим інтегралом, наведено на рисунку$\PageIndex{2}$.

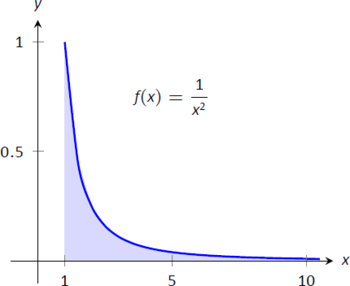
$imageedit_7_6961301863.png$

Малюнок$\PageIndex{2}$: Графік$f(x) = \frac{1}{x^2}$ у прикладі$\PageIndex{1}$.

\[\begin{align} \int_1^\infty \frac1x\ dx & = \lim_{b\to\infty}\int_1^b\frac1x\ dx \\ &= \lim_{b\to\infty} \ln |x|\Big|_1^b \\ &= \lim_{b\to\infty} \ln (b)\\ &= \infty. \end{align}\]Межі не існує, отже, неправильний інтеграл$\int_1^\infty\frac1x\ dx$ розходиться. Порівняйте графіки на малюнках$\PageIndex{3a}$ і$\PageIndex{3b}$; зверніть увагу, як графік$f(x) = 1/x$ помітно більше. Цієї різниці достатньо для того, щоб неправильний інтеграл розходився.

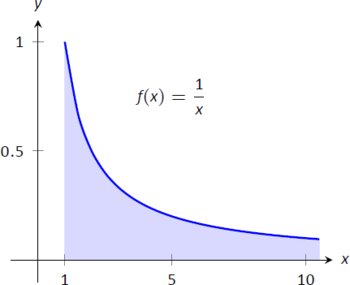
$imageedit_26_7628100093.png$

Малюнок$\PageIndex{3}$: Графік$f(x) = \frac{1}{x}$ у прикладі$\PageIndex{1}$

\[\begin{align} \int_{-\infty}^0 e^x \ dx &= \lim_{a\to-\infty} \int_a^0e^x\ dx \\ &= \lim_{a\to-\infty} e^x\Big|_a^0 \\ &= \lim_{a\to-\infty} e^0-e^a \\&= 1. \end{align}\]Графік площі, визначеної цим інтегралом, наведено на рисунку$\PageIndex{4}$.

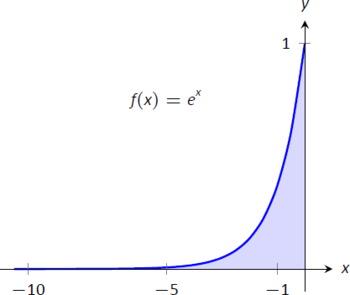
$imageedit_16_2996739365.png$

Малюнок$\PageIndex{4}$: Графік$f(x) = e^x$ у прикладі$\PageIndex{1}$

Нам потрібно буде розбити це на два неправильних інтеграли і вибрати значення$c$, як у частині 3 Визначення$\PageIndex{1}$. Будь-яке значення$c$ добре; ми вибираємо$c=0$. \[\begin{align} \int_{-\infty}^\infty \frac1{1+x^2}\ dx &= \lim_{a\to-\infty} \int_a^0\frac{1}{1+x^2}\ dx + \lim_{b\to\infty} \int_0^b\frac{1}{1+x^2}\ dx \\ &= \lim_{a\to-\infty} \tan^{-1}x\Big|_a^0 + \lim_{b\to\infty} \tan^{-1}x\Big|_0^b\\ &= \lim_{a\to-\infty} \left(\tan^{-1}0-\tan^{-1}a\right) + \lim_{b\to\infty} \left(\tan^{-1}b-\tan^{-1}0\right)\\ &= \left(0-\frac{-\pi}2\right) + \left(\frac{\pi}2-0\right).\end{align}\]Кожна межа існує, отже вихідний інтеграл сходиться і має значення:\[= \pi.\] Графік площі, визначеної цим інтегралом, наведено на рисунку$\PageIndex{5}$.

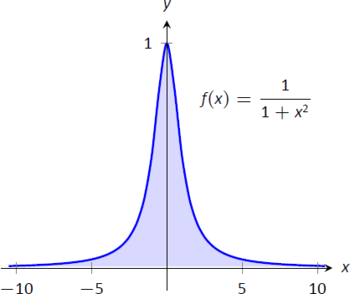
$imageedit_21_6367901671.png$

Малюнок$\PageIndex{5}$: Графік$f(x) = \frac{1}{1+x^2}$ у прикладі$\PageIndex{1}$

У попередньому розділі було введено правило L'Hôpital, метод оцінки лімітів, які повертають невизначені форми. Це не рідкість, коли межі, що виникають внаслідок неправильних інтегралів, потребують цього правила, як показано далі.

Приклад$\PageIndex{2}$: Improper integration and L'Hôpital's Rule

Оцініть неправильний інтеграл

\[\int_1^\infty \frac{\ln x}{x^2}\ dx.\]

Рішення

Цей інтеграл вимагатиме використання інтеграції частинами. Нехай$u = \ln x$ і$dv = 1/x^2\ dx$. Тоді

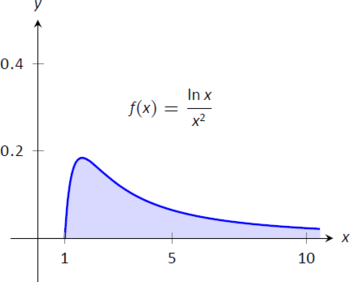
$imageedit_31_8641782108.png$

Малюнок$\PageIndex{6}$: Графік$f(x) = \frac{\ln x}{x^2}$ у прикладі$\PageIndex{2}$

\[\begin{align}\int_1^\infty\frac{\ln x}{x^2}\ dx &= \lim_{b\to\infty}\int_1^b\frac{\ln x}{x^2}\ dx \\ &= \lim_{b\to\infty}\left(-\frac{\ln x}{x}\Big|_1^b +\int_1^b \frac{1}{x^2} \ dx \right)\\ &= \lim_{b\to\infty} \left.\left(-\frac{\ln x}{x} -\frac1x\right)\right|_1^b\\ &= \lim_{b\to\infty} \left(-\frac{\ln b}{b}-\frac1b - \left(-\ln 1-1\right)\right).\end{align}\]

$\ln 1$Терміни$1/b$ та переходять до 0, залишаючи$ \lim_{b\to\infty} -\frac{\ln b}b + 1.$ Нам потрібно оцінити за$ \lim_{b\to\infty} \frac{\ln b}{b}$ допомогою правила L'Hôpital. У нас є:

\[\begin{align} \lim_{b\to\infty}\frac{\ln b}b &\stackrel{\ \text{ by LHR } \ }{=} \lim_{b\to\infty} \frac{1/b}{1} \\ &= 0.\end{align}\]

Таким чином, неправильний інтеграл оцінюється як:

\[\int_1^\infty\frac{\ln x}{x^2}\ dx = 1.\]

Неправильні інтеграли з нескінченною дальністю

Ми щойно розглянули певні інтеграли, де інтервал інтеграції був нескінченним. Зараз ми розглянемо ще один тип неправильної інтеграції, де діапазон integrand нескінченний.

Визначення$\PageIndex{2}$: Improper Integration with Infinite Range

{$f(x)$Дозволяти бути неперервна функція на$[a,b]$ крім at$c$$a\leq c\leq b$,$x=c$ де вертикальна асимптота$f$. Визначте

\[\int_a^b f(x)\ dx = \lim_{t\to c^-}\int_a^t f(x)\ dx + \lim_{t\to c^+}\int_t^b f(x)\ dx.\]

Приклад$\PageIndex{3}$: Improper integration of functions with infinite range

Оцініть такі неправильні інтеграли:

$ 1.\ \int_0^1\frac1{\sqrt{x}}\ dx \hskip 50pt 2. \ \int_{-1}^1\frac{1}{x^2}\ dx.$

Рішення

Графік$f(x) = 1/\sqrt{x}$ наведено на рисунку$\PageIndex{7}$. Зверніть увагу, що$f$ має вертикальну асимптоту в$x=0$; в деякому сенсі, ми намагаємося обчислити область, яка не має «вершини». Чи може це мати кінцеве значення? \[\begin{align} \int_0^1 \frac{1}{\sqrt{x}}\ dx &= \lim_{a\to0^+}\int_a^1 \frac1{\sqrt{x}}\ dx \\&=\lim_{a\to0^+} 2\sqrt{x}\Big|_a^1 \\ &= \lim_{a\to0^+} 2\left(\sqrt{1}-\sqrt{a}\right)\\ &= 2.\end{align}\]
Виявляється, область має кінцеву площу, хоча вона не має верхньої межі (дивні речі можуть статися в математиці при розгляді нескінченного).
Примітка: У$\PageIndex{1}$ визначенні$c$ може бути одна з кінцевих точок ($a$або$b$). У такому випадку існує лише одна межа, яку слід розглядати як частину визначення.

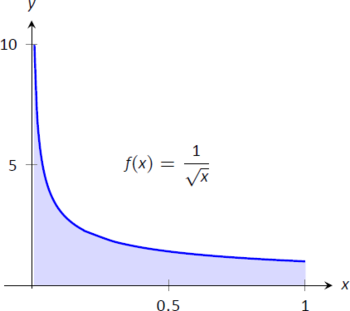
$imageedit_36_3498543493.png$

Малюнок$\PageIndex{7}$: Графік$f(x)=\frac{1}{\sqrt{x}}$ у прикладі$\PageIndex{3}$

Функція$f(x) = 1/x^2$ має вертикальну асимптоту при$x=0$, як показано на малюнку$\PageIndex{8}$, тому цей інтеграл є неправильним інтегралом. Давайте уникнути використання обмежень на мить і продовжити, не визнаючи неправильну природу інтеграла. Це призводить до:\[\begin{align}\int_{-1}^1\frac1{x^2}\ dx &= -\frac1x\Big|_{-1}^1\\ &= -1 - (1)\\ &=-2 ! \end{align}\] Очевидно, що область, про яку йде мова, знаходиться вище$x$ -осі, але область нібито негативна! Чому наша відповідь не відповідає нашій інтуїції? Щоб відповісти на це, оцініть інтеграл за допомогою Definition$\PageIndex{2}$. \[\begin{align} \int_{-1}^1\frac1{x^2}\ dx &= \lim_{t\to0^-}\int_{-1}^t \frac1{x^2}\ dx + \lim_{t\to0^+}\int_t^1\frac1{x^2}\ dx \\ &= \lim_{t\to0^-}-\frac1x\Big|_{-1}^t + \lim_{t\to0^+}-\frac1x\Big|_t^1\\ &= \lim_{t\to0^-}-\frac1t-1 + \lim_{t\to0^+} -1+\frac1t\\ &\Rightarrow \Big(\infty-1\Big)\ + \ \Big(- 1+\infty\Big).\end{align}\]Жодна межа не сходиться, отже, оригінальний неправильний інтеграл розходиться. Безглузда відповідь, яку ми отримали, ігноруючи неправильну природу інтеграла, є саме таким: безглуздим.

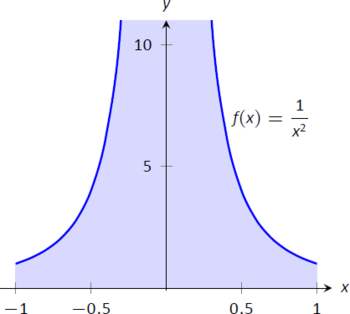
$imageedit_41_7694253586.png$

Малюнок$\PageIndex{8}$: Графік$f(x)=\frac{1}{x^2}$ у прикладі$\PageIndex{3}$

Розуміння конвергенції та розбіжності

Часто ми зацікавлені в тому, щоб просто знати, чи збігається неправильний інтеграл, і не обов'язково значення збіжною інтеграла. Ми пропонуємо тут кілька інструментів, які допомагають визначити збіжність або розбіжність неправильних інтегралів без інтеграції.

Наш перший інструмент - зрозуміти поведінку функцій форми$ \frac1{x\hskip1pt ^p}$.

Приклад$\PageIndex{4}$: Improper integration of $1/x^p$

Визначте значення,$p$ для яких$\int_1^\infty \frac1{x\hskip1pt ^p}\ dx$ сходиться.

Рішення

Ми починаємо з інтеграції, а потім оцінки межі.

\[\begin{align} \int_1^\infty \frac1{x\hskip1pt ^p}\ dx &= \lim_{b\to\infty}\int_1^b\frac1{x\hskip1pt ^p}\ dx\\ &= \lim_{b\to\infty}\int_1^b x^{-p}\ dx \qquad \text{(assume $p\neq 1$)}\\&= \lim_{b\to\infty} \frac{1}{-p+1}x^{-p+1}\Big|_1^b\\ &= \lim_{b\to\infty} \frac{1}{1-p}\big(b\hskip1pt^{1-p}-1^{1-p}\big).\\\end{align}\]

Коли ця межа сходиться — тобто коли ця межа немає$\infty$? Ця межа сходиться саме тоді,$b$ коли потужність менше 0: коли$1-p<0 \Rightarrow 1<p$.

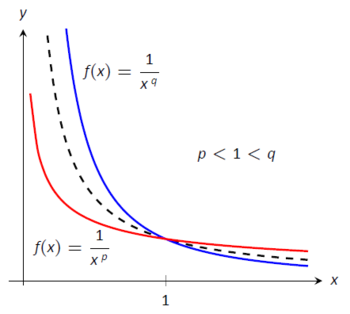
$imageedit_45_4006079714.png$

Малюнок$\PageIndex{9}$: Побудова функцій форми$1/x\,^p$ у прикладі$\PageIndex{4}$

Наш аналіз показує, що якщо$p>1$, то$\int_1^\infty \frac1{x\hskip1pt ^p}\ dx $ сходиться. Коли$p<1$ неправильний інтеграл розходиться; ми показали в прикладі$\PageIndex{1}$, що коли$p=1$ інтеграл також розходиться.

$\PageIndex{9}$Малюйте графіки$y=1/x$ з пунктирною лінією разом з графіками$y=1/x^p$$p<1$, і$y=1/x^q$,$q>1$. Якось пунктирна лінія утворює розділову лінію між збіжністю і розбіжністю.

Результат Прикладу$\PageIndex{4}$ дає важливий інструмент у визначенні збіжності інших інтегралів. Аналогічний результат доведено у вправах про неправильні інтеграли форми$\int_0^1\frac1{x\hskip1pt ^p}\ dx$. Ці результати узагальнені в наступній Ключовій ідеї.

Ключова ідея 21: збіжність неправильних інтегралів$\int_1^\infty\frac1{x\hskip1pt ^p}\ dx$ and $\int_0^1\frac1{x\hskip1pt ^p}\ dx$.

Неправильний інтеграл$\int_1^\infty\frac1{x\hskip1pt ^p}\ dx$ сходиться, коли$p>1$ і розходиться, коли$p\leq 1.$
Неправильний інтеграл$\int_0^1\frac1{x\hskip1pt ^p}\ dx$ сходиться, коли$p<1$ і розходиться, коли$p\geq 1.$

Основною методикою визначення збіжності неправильних інтегралів є порівняння цілісного, збіжність якого невідома цілісності, збіжність якого відома. Ми часто використовуємо integrands форми$1/x\hskip1pt ^p$ для порівняння, оскільки їх збіжність на певних інтервалах відома. Це описано в наступній теоремі.

Теорема$\PageIndex{1}$: Direct Comparison Test for Improper Integrals

Нехай$f$ і$g$ бути безперервним на$[a,\infty)$ де$0\leq f(x)\leq g(x)$ для всіх$x$ в$[a,\infty)$.

Якщо$ \int_a^\infty g(x)\ dx$ сходиться, то$\int_a^\infty f(x)\ dx$ сходиться.
Якщо$ \int_a^\infty f(x)\ dx$ розходиться, то$ \int_a^\infty g(x)\ dx$ розходиться.

Примітка: Для зручності ми використовували верхню і нижню межу «1" в Key Idea 21. Його можна замінити будь-яким$a$ де завгодно$a>0$.

Приклад$\PageIndex{5}$: Determining convergence of improper integrals

Визначте збіжність наступних неправильних інтегралів.

$ \int_1^\infty e^{-x^2}\ dx$
$ \int_3^\infty \frac{1}{\sqrt{x^2-x}}\ dx$

Рішення

Функція$f(x) = e^{-x^2}$ не має антипохідної, що виражається з точки зору елементарних функцій, тому ми не можемо інтегрувати безпосередньо. Це можна порівняти з$g(x)=1/x^2$, і як продемонстровано на малюнку$\PageIndex{10}$,$e^{-x^2} < 1/x^2$ на$[1,\infty)$. Ми знаємо з Key Idea 21, яка$\int_1^\infty \frac{1}{x^2}\ dx$ сходиться, отже,$\int_1^\infty e^{-x^2}\ dx$ також сходиться.

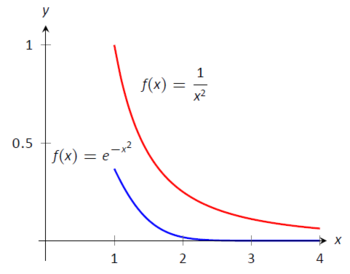
$imageedit_49_8396325811.png$

Малюнок$\PageIndex{10}$: Графіки$f(x) = e^{-x^2}$ і$f(x)= 1/x^2$ в прикладі$\PageIndex{6}$

Відзначимо, що для великих значень$x$,$ \frac{1}{\sqrt{x^2-x}} \approx \frac{1}{\sqrt{x^2}} =\frac{1}{x}$. Ми знаємо з Key Idea 21 та наступної ноти, яка$\int_3^\infty \frac1x\ dx$ розходиться, тому ми прагнемо порівняти оригінальний integrand з$1/x$.
Легко помітити, що коли$x>0$, ми маємо$x = \sqrt{x^2} > \sqrt{x^2-x}$. Прийняття взаємних обертає нерівність, даючи $$\ frac1x <\ frac1 {\ sqrt {x^2-x}}. $$
Використовуючи теорему$\PageIndex{1}$, ми робимо висновок, що оскільки$\int_3^\infty\frac1x\ dx$$\int_3^\infty\frac1{\sqrt{x^2-x}}\ dx$ розходиться, також розходиться. Малюнок$\PageIndex{11}$ ілюструє це.

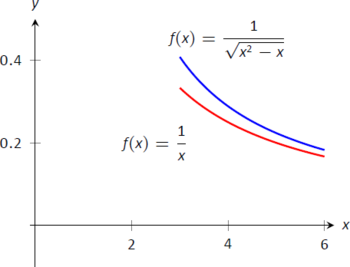
$imageedit_54_5068653121.png$

Малюнок$\PageIndex{11}$: Графіки$f(x) = 1/\sqrt{x^2-x}$ і$f(x)= 1/x$ в прикладі$\PageIndex{5}$

Можливість порівнювати «невідомі» інтеграли з «відомими» інтегралами дуже корисна при визначенні збіжності. Однак деякі з наших прикладів були трохи «занадто приємними». Наприклад, це було зручно$\frac{1}x < \frac{1}{\sqrt{x^2-x}}$, але що робити, якщо "$-x$" замінено на "$+2x+5$«? Тобто, що вже говорити про зближення$\int_3^\infty\frac{1}{\sqrt{x^2+2x+5}}\ dx$? Ми маємо$\frac{1}{x} > \frac1{\sqrt{x^2+2x+5}}$, тому ми не можемо використовувати теорему$\PageIndex{1}$.

У таких випадках (і багатьох інших) корисно використовувати наступну теорему.

Теорема: Тест граничного порівняння для неправильних інтегралів

$f$$g$Дозволяти і бути безперервними функціями на$[a,\infty)$ де$f(x)>0$ і$g(x)>0$ назавжди$x$. Якщо

\[\lim_{x\to\infty} \frac{f(x)}{g(x)} = L,\qquad 0<L<\infty,\]

потім

\[\int_a^\infty f(x)\ dx \quad \text{and} \quad \int_a^\infty g(x)\ dx\]

або обидва сходяться, або обидва розходяться.

Приклад$\PageIndex{6}$: Determining convergence of improper integrals

Визначаємо збіжність$\int_3^{\infty} \frac{1}{\sqrt{x^2+2x+5}}\ dx$.

Рішення

Коли$x$ стає великим, квадратична всередині функції квадратного кореня почне вести себе так само, як$y=x$. Отже, ми порівняємо$\frac{1}{\sqrt{x^2+2x+5}}$\ to$\frac1x$ з тестом порівняння лімітів:

$\ lim_ {x\ to\ infty}\ frac {1/\ sqrt {x^2+2x+5}} {1/x} =\ lim_ {x\ to\ infty}\ frac {x} {\ sqrt {x^2+2x+5}}.\]

Безпосередня оцінка цього ліміту повертає$\infty/\infty$, невизначену форму. Використання правила L'Hôpital здається доречним, але в цій ситуації це не призводить до корисних результатів. (Ми закликаємо читача використовувати правило L'Hôpital принаймні один раз, щоб перевірити це.)

Біда - функція квадратного кореня. Щоб позбутися від неї, ми використовуємо наступний факт: Якщо$\lim_{x\to c} f(x) = L$, то$\lim_{x\to c} f(x)^2 = L^2$. (Це вірно, коли$c$ або$L$ є$\infty$.) Отже, розглянемо тепер ліміт\)

$\ lim_ {x\ to\ infty}\ frac {x^2} {x^2+2x+5}.\]

Це сходиться до 1, тобто початкова межа також зійшлася до 1. Оскільки$x$ вона стає дуже великою, функція$\frac{1}{\sqrt{x^2+2x+5}}$ виглядає дуже схожа$\frac1x.$ Оскільки ми знаємо, що це$\int_3^{\infty} \frac1x\ dx$ розходиться, за тестом порівняння обмежень ми знаємо, що$\int_3^\infty\frac{1}{\sqrt{x^2+2x+5}}\ dx$ також розходиться. Малюнок$\PageIndex{12}$ графіків$f(x)=1/\sqrt{x^2+2x+5}$ і$f(x)=1/x$, ілюструючи, що, як$x$ стає великим, функції стають нерозрізненими.

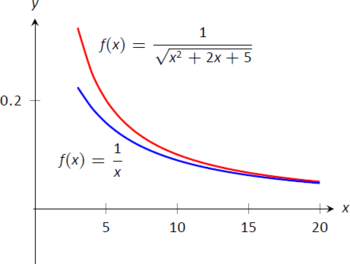
$imageedit_63_6708446532.png$

Малюнок$\PageIndex{12}$: Графік$f(x)=\frac{1}{\sqrt{x^2+2x+5}}$ і$f(x)=\frac1x$ в прикладі$\PageIndex{6}$.

Обидва тести прямого та граничного порівняння були наведені через інтеграли через нескінченний інтервал. Є версії, які застосовуються до неправильних інтегралів з нескінченним діапазоном, але оскільки вони трохи багатослівні і трохи складніші в застосуванні, вони опускаються з цього тексту.

У цій главі досліджено багато методів інтеграції. Ми дізналися Заміна, яка «скасовує» правило диференціації ланцюга, а також інтеграцію частинами, що «скасовує» Правило продукту. Ми вивчили спеціалізовані методи обробки тригонометричних функцій і представили гіперболічні функції, які тісно пов'язані з тригонометричними функціями. Всі методи ефективно мають цю спільну мету: перепишіть integrand по-новому, щоб крок інтеграції було легше побачити та реалізувати.

Як говорилося раніше, інтеграція, загалом, важка. Легко написати функцію, антидериватив якої неможливо записати з точки зору елементарних функцій, і навіть коли функція має антипохідну, що виражається елементарними функціями, може бути дуже важко виявити, що це таке. Потужна система комп'ютерної алгебри Mathematica має приблизно 1000 сторінок коду, присвяченого інтеграції.

Не дозволяйте цій складності відлякувати вас. Існує велике значення в навчанні інтеграційних методів, оскільки вони дозволяють маніпулювати інтегралом способами, які можуть висвітлити концепцію для більшого розуміння. Також велике значення має розуміння необхідності хороших числових методів: Трапецієподібні та Сімпсонові Правила - це лише початок потужних методів наближення значення інтеграції.

У наступному розділі наголошується на використанні інтеграції. Як правило, ми не знаходимо антипохідні заради антидеривативів, а скоріше тому, що вони забезпечують вирішення певного типу проблеми. Наступна глава знайомить нас з низкою різних проблем, вирішення яких забезпечується інтеграцією.