6.6: Гіперболічні функції

Last updated
Save as PDF

Page ID: 60813

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Гіперболічні функції - це набір функцій, які мають безліч застосувань до математики, фізики та техніки. Серед багатьох інших застосувань вони використовуються для опису формування супутникових кілець навколо планет, для опису форми мотузки, що звисає з двох точок, і мають застосування до теорії спеціальної відносності. Цей розділ визначає гіперболічні функції та описує багато їх властивостей, особливо їх корисність для обчислення.

Ці функції іноді називають «гіперболічними тригонометричними функціями», оскільки між ними та стандартними тригонометричними функціями існує багато, багато зв'язків. Малюнок$\PageIndex{1}$ демонструє одне таке з'єднання. Подібно до того, як косинус і синус використовуються для визначення точок на колі$x^2+y^2=1$, визначеному, функції гіперболічний косинус і гіперболічний синус використовуються для визначення точок на гіперболі$x^2-y^2=1$.

$альт$ $альт$

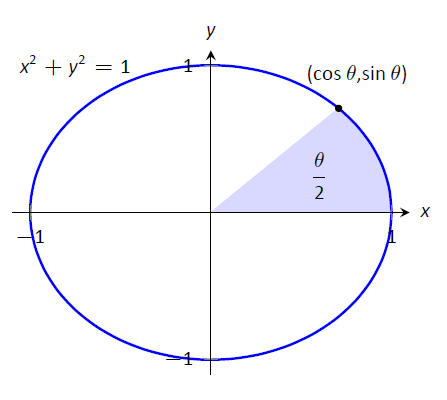
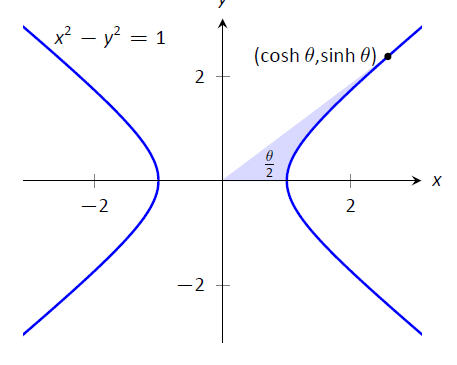
Рисунок$\PageIndex{1}$: Використання тригонометричних функцій для визначення точок на колі та гіперболічних функцій для визначення точок на гіперболі. Площа затінених областей включається в них.

Почнемо з їх визначення.

Визначення$\PageIndex{1}$: Hyperbolic Functions

$ \cosh x = \frac{e^x+e^{-x}}2$
$ \sinh x = \frac{e^x-e^{-x}}2$
$\tanh x = \frac{\sinh x}{\cosh x}$
$ \text{sech} x = \frac{1}{\cosh x}$
$ \text{csch} x = \frac{1}{\sinh x}$
$ \coth x = \frac{\cosh x}{\sinh x}$

Ці гіперболічні функції зображені на малюнку$\PageIndex{2}$. У графіки$\cosh x$ і$\sinh x$, графіки$e^x/2$ і$e^{-x}/2$ включаються пунктирними лініями. Як$x$ отримує «великий»,$\cosh x$ і$\sinh x$ кожен діє як$e^x/2$; коли$x$ є великим від'ємним числом,$\cosh x$ діє так$e^{-x}/2$, як $\ sinh x$ діє як$-e^{-x}/2$.

Зверніть увагу на області$\tanh x$ і$\text{sech} x$ є$(-\infty,\infty)$, тоді як обидва$\coth x$ і$\text{csch} x$ мають вертикальні асимптоти в$x=0$. Також зверніть увагу на діапазони цих функцій, особливо$\tanh x$: як$x\to\infty$, обидва$\sinh x$ і$\cosh x$ підхід$e^{-x}/2$, звідси$\tanh x$ підходи$1$.

Наступний приклад досліджує деякі властивості цих функцій, які мають чудову схожість з властивостями їх тригонометричних аналогів.

Примітка вимови: «кош» римується з «gosh», «sinh» римується з «pinch», а «tanh» римується з «ранчо».

$альт$

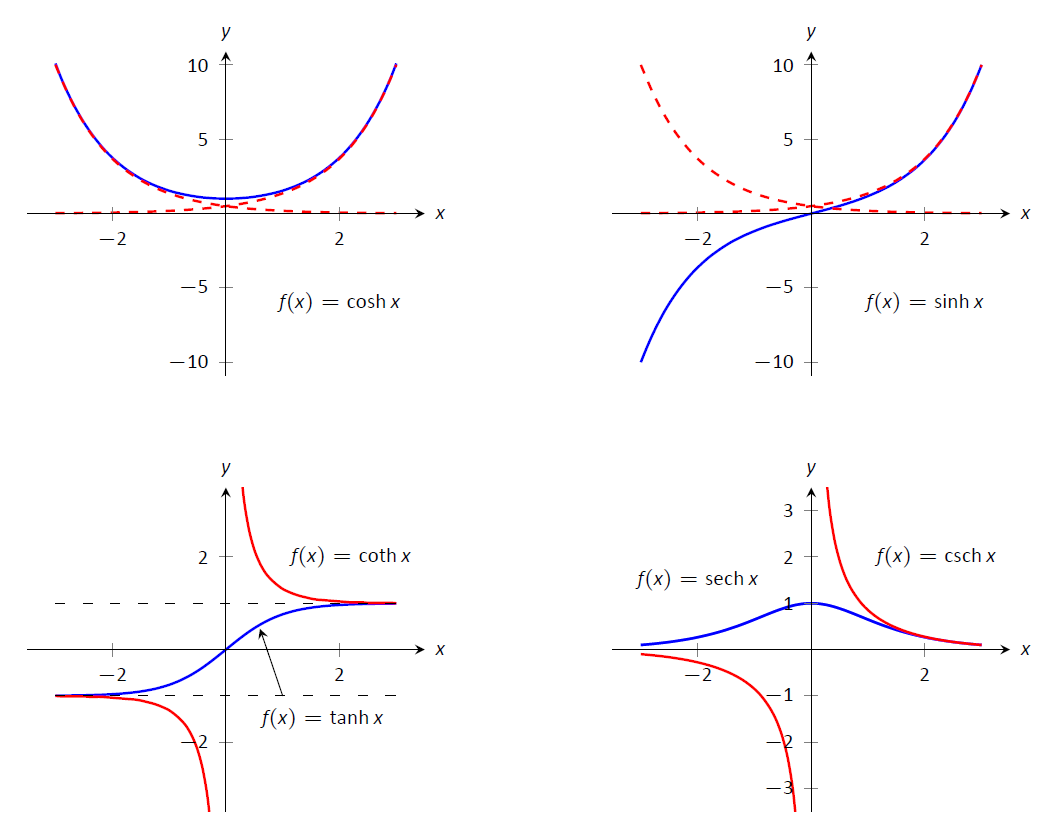
Малюнок$\PageIndex{2}$: Графіки гіперболічних функцій.

Приклад$\PageIndex{1}$: Exploring properties of hyperbolic functions

Використовуйте Definition,$\PageIndex{1}$ щоб переписати такі вирази.

$\cosh^2 x-\sinh^2x$
$\tanh^2 x+\text{sech}^2 x$
$2\cosh x\sinh x$
$\frac{d}{dx}\big(\cosh x\big)$
$\frac{d}{dx}\big(\sinh x\big)$
$\frac{d}{dx}\big(\tanh x\big)$

Рішення

\[\begin{align} \cosh^2x-\sinh^2x &= \left(\frac{e^x+e^{-x}}2\right)^2 -\left(\frac{e^x-e^{-x}}2\right)^2\\ &= \frac{e^{2x}+2e^xe^{-x} + e^{-2x}}4 - \frac{e^{2x}-2e^xe^{-x} + e^{-2x}}4\\ &= \frac44=1.\end{align}\]Отже$\cosh^2 x-\sinh^2x=1$.
\[\begin{align} \tanh^2 x+\text{sech}^2 x &=\frac{\sinh^2x}{\cosh^2 x} + \frac{1}{\cosh^2 x} \\ &= \frac{\sinh^2x+1}{\cosh^2 x}\qquad \text{Now use identity from #1.}\\ &= \frac{\cosh^2 x}{\cosh^2 x} = 1. \end{align}\]Отже$\tanh^2 x+\text{sech}^2 x=1$.
\[\begin{align} 2\cosh x\sinh x &= 2\left(\frac{e^x+e^{-x}}2\right)\left(\frac{e^x-e^{-x}}2\right) \\ &= 2 \cdot\frac{e^{2x} - e^{-2x}}4\\ &= \frac{e^{2x} - e^{-2x}}2 = \sinh (2x).\\ \end{align}\]Таким чином$2\cosh x\sinh x = \sinh (2x)$.
\[\begin{align} \frac{d}{dx}\big(\cosh x\big) &= \frac{d}{dx}\left(\frac{e^x+e^{-x}}2\right) \\ &= \frac{e^x-e^{-x}}2\\ &= \sinh x. \end{align}\]Так$\frac{d}{dx}\big(\cosh x\big) = \sinh x.$
\[\begin{align} \frac{d}{dx}\big(\sinh x\big) &= \frac{d}{dx}\left(\frac{e^x-e^{-x}}2\right) \\ &= \frac{e^x+e^{-x}}2\\ &= \cosh x. \end{align}\]Так$\frac{d}{dx}\big(\sinh x\big) = \cosh x.$
\[\begin{align} \frac{d}{dx}\big(\tanh x\big) &= \frac{d}{dx}\left(\frac{\sinh x}{\cosh x}\right) \\ &= \frac{\cosh x \cosh x - \sinh x \sinh x}{\cosh^2 x}\\ &= \frac{1}{\cosh^2 x}\\ &=\text{sech}^2 x. \end{align}\]Так$\frac{d}{dx}\big(\tanh x\big) = \text{sech}^2 x.$

Наступна ключова ідея узагальнює багато важливих ідентичностей, що стосуються гіперболічних функцій. Кожен може бути перевірений, звернувшись до Визначення$\PageIndex{1}$.

Ключова ідея 16: Корисні властивості гіперболічної функції

Основні тотожності

$\cosh^2x-\sinh^2x=1$
$\tanh^2x+\text{sech}^2x=1$
$\coth^2x-\text{csch}^2x = 1$
$\cosh 2x=\cosh^2x+\sinh^2x$
$\sinh 2x = 2\sinh x\cosh x$
$\cosh^2x = \frac{\cosh 2x+1}{2}$
$\sinh^2x=\frac{\cosh 2x-1}{2}$

похідні

$\frac{d}{dx}\big(\cosh x\big) = \sinh x$
$\frac{d}{dx}\big(\sinh x\big) = \cosh x$
$\frac{d}{dx}\big(\tanh x\big) = \text{sech}^2 x$
$\frac{d}{dx}\big(\text{sech} x\big) = -\text{sech} x\tanh x$
$\frac{d}{dx}\big(\text{csch} x\big) = -\text{csch} x\coth x$
$\frac{d}{dx}\big(\coth x\big) = -\text{csch}^2x$

Інтеграли

$\int \cosh x\ dx = \sinh x+C$
$\int \sinh x\ dx = \cosh x+C$
$\int \tanh x\ dx = \ln(\cosh x) +C$
$\int \coth x\ dx = \ln|\sinh x\,|+C$

Практикуємо використання Key Idea 16

Приклад$\PageIndex{2}$: Derivatives and integrals of hyperbolic functions

Оцініть наступні похідні та інтеграли.

$\frac{d}{dx}\big(\cosh 2x\big)$
$\int \text{sech}^2(7t-3)\ dt$
$ \int_0^{\ln 2} \cosh x\ dx$

Рішення

Використовуючи правило ланцюга безпосередньо, ми маємо$\frac{d}{dx} \big(\cosh 2x\big) = 2\sinh 2x$.
Просто щоб продемонструвати, що це працює, давайте також використаємо базову ідентифікацію, знайдену в Key Idea 16:$\cosh 2x = \cosh^2x+\sinh^2x$.
\[\begin{align}\frac{d}{dx}\big(\cosh 2x\big) = \frac{d}{dx}\big(\cosh^2x+\sinh^2x\big) &= 2\cosh x\sinh x+ 2\sinh x\cosh x\\ &= 4\cosh x\sinh x.\end{align}\]Використовуючи іншу базову ідентичність, ми можемо це побачити$4\cosh x\sinh x = 2\sinh 2x$. Ми отримуємо однакову відповідь в будь-якому випадку.
Ми використовуємо заміну, з$u = 7t-3$ і$du = 7dt$. Застосовуючи ключові ідеї 10 і 16 ми маємо:
$\ int\ text {sech} ^2 (7t-3)\ dt =\ frac17\ tanh (7t-3) + C.$$
$$\ int_0^ {\ ln 2}\ кош х\ dx =\ сінх х\ Біг|_0^ {\ ln 2} =\ sinh (\ ln 2) -\ sinh 0 =\ sinh (\ ln 2). $$
Ми можемо спростити цей останній вираз, як$\sinh x$ базується на показниках:
$$\ sinh (\ ln 2) =\ frac {e^ {\ ln 2} -e^ {-\ ln 2}} 2 =\ frac {2-1/2} {2} =\ frac34. $$

Обернені гіперболічні функції

Подібно до того, як обернені тригонометричні функції корисні в певних інтеграціях, зворотні гіперболічні функції корисні з іншими. На малюнку 16 показані обмеження доменів, щоб зробити кожну функцію один-на-один, а також отримані домени та діапазони їх обернених функцій. Їх графіки наведені на малюнку$\PageIndex{3}$

Оскільки гіперболічні функції визначаються термінами експоненціальних функцій, їх зворотні можуть бути виражені термінами логарифмів, як показано в Key Idea 17. Це часто зручніше посилатися,$\sinh^{-1}x$ ніж на$\ln\big(x+\sqrt{x^2+1}\big)$, особливо коли людина працює над теорією і не потрібно обчислювати фактичні значення. З іншого боку, коли потрібні обчислення, технологія часто корисна, але багато ручних калькуляторів не мають$\sinh^{-1}x$ кнопки\ textit {зручно}. (Часто до нього можна отримати доступ за системою меню, але не зручно.) У такій ситуації стане в нагоді логарифмічне подання. Читачеві не рекомендується запам'ятовувати їх, а скоріше знати, що вони існують, і знати, як їх використовувати, коли це необхідно.

$альт$

Таблиця$\PageIndex{1}$:$\cosh x$ Графіки$\sinh x$ та їх зворотні.

$альт$

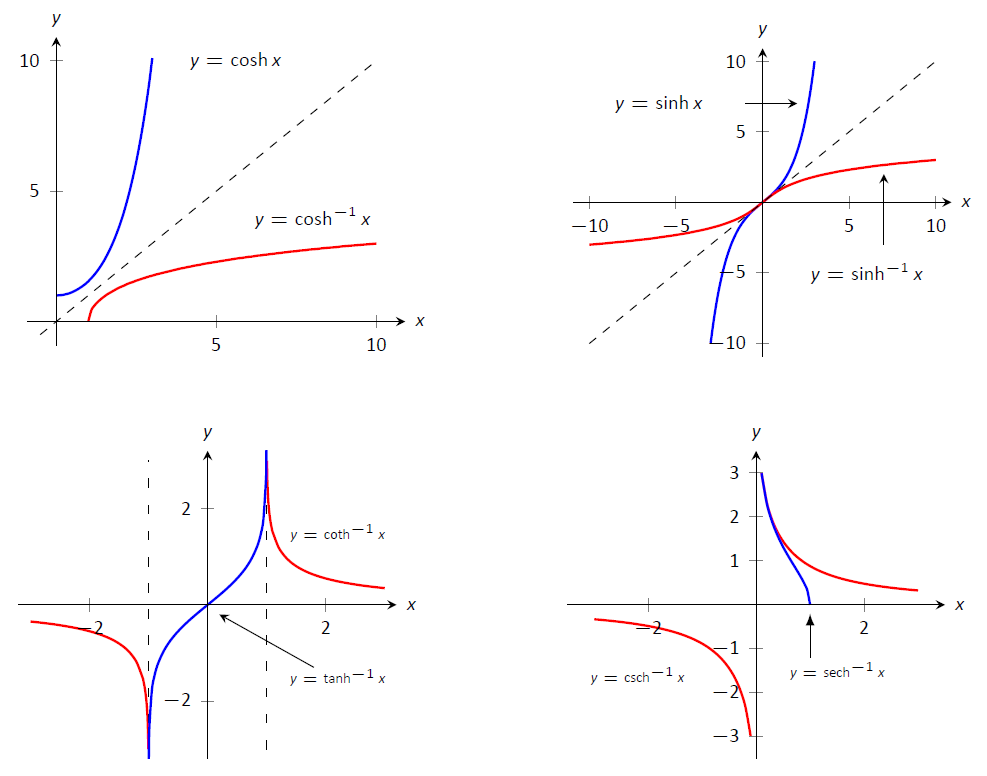
Малюнок$\PageIndex{3}$: Графіки гіперболічних функцій та їх обернень.

Наступні Ключові ідеї дають похідні та інтеграли, що стосуються обернених гіперболічних функцій. У Key Idea 19 наведено зворотні гіперболічні та логарифмічні зображення антипохідної функції на основі Key Idea 17. Знову ж таки, ці останні функції часто більш корисні, ніж перші. Зверніть увагу, як обернені гіперболічні функції можуть бути використані для розв'язання інтегралів, які ми використовували тригонометричну заміну для розв'язання в розділі 6.4.

Key IDeA 17: Логарифмічні визначення обернених гіперболічних функцій.

$\cosh^{-1}x=\ln\big(x+\sqrt{x^2-1}\big);\ x\geq1$
$\tanh^{-1}x = \frac12\ln\left(\frac{1+x}{1-x}\right);\ |x|<1$
$\text{sech}^{-1}x = \ln\left(\frac{1+\sqrt{1-x^2}}x\right);\ 0<x\leq1$
$\sinh^{-1}x = \ln\big(x+\sqrt{x^2+1}\big)$
$\coth^{-1}x = \frac12\ln\left(\frac{x+1}{x-1}\right);\ |x|>1$
$\text{csch}^{-1}x = \ln\left(\frac1x+\frac{\sqrt{1+x^2}}{|x|}\right);\ x\neq0$

Ключова ідея 18: Похідні за участю обернених гіперболічних функцій

$\frac{d}{dx}\big(\cosh^{-1} x\big) = \frac{1}{\sqrt{x^2-1}};\ x>1$
$\frac{d}{dx}\big(\sinh^{-1} x\big) = \frac{1}{\sqrt{x^2+1}}$
$\frac{d}{dx}\big(\tanh^{-1} x\big) = \frac{1}{1-x^2};\ |x|<1$
$\frac{d}{dx}\big(\text{sech}^{-1} x\big) = \frac{-1}{x\sqrt{1-x^2}}; 0<x<1$
$\frac{d}{dx}\big(\text{csch}^{-1} x\big) = \frac{-1}{|x|\sqrt{1+x^2}};\ x\neq0$
$\frac{d}{dx}\big(\coth^{-1} x\big) = \frac{1}{1-x^2};\ |x|>1$

Ключова ідея 19: Інтеграли за участю обернених гіперболічних функцій

$\int \frac{1}{\sqrt{x^2-a^2}}\ dx$$=\qquad \cosh^{-1}\left(\frac xa\right)+C;\ 0<a<x$$\quad=\ln\Big|x+\sqrt{x^2-a^2}\Big|+C$
$\int \frac{1}{\sqrt{x^2+a^2}}\ dx$$=\qquad \sinh^{-1}\left(\frac xa\right)+C;\ a>0$$\qquad=\ln\Big|x+\sqrt{x^2+a^2}\Big|+C$
$\int \frac{1}{a^2-x^2}\ dx$$=\qquad \left\{\begin{array}{ccc} \frac1a\tanh^{-1}\left(\frac xa\right)+C & & x^2<a^2 \\ \\\frac1a\coth^{-1}\left(\frac xa\right)+C & & a^2<x^2 \end{array}\right.$$\quad=\frac1{2a}\ln\left|\frac{a+x}{a-x}\right|+C$
$\int \frac{1}{x\sqrt{a^2-x^2}}\ dx $$=\qquad -\frac1a\text{sech}^{-1}\left(\frac xa\right)+C;\ 0<x<a$$\quad= \frac1a \ln\left(\frac{x}{a+\sqrt{a^2-x^2}}\right)+C $
$\int \frac{1}{x\sqrt{x^2+a^2}}\ dx$$=\qquad -\frac1a\text{csch}^{-1}\left|\frac xa\right| + C;\ x\neq 0,\ a>0$$\quad= \frac1a \ln\left|\frac{x}{a+\sqrt{a^2+x^2}}\right|+C$

Ми практикуємо використання похідних і інтегральних формул в наступному прикладі.

Приклад$\PageIndex{3}$: Derivatives and integrals involving inverse hyperbolic functions

Оцініть наступне.

$ \frac{d}{dx}\left[\cosh^{-1}\left(\frac{3x-2}{5}\right)\right]$
$ \int\frac{1}{x^2-1}\ dx$
$ \int \frac{1}{\sqrt{9x^2+10}}\ dx$

Рішення

Застосування ключової ідеї 18 з правилом ланцюга дає:
$\ frac {d} {dx}\ лівий [\ cosh^ {-1}\ лівий (\ frac {3x-2} 5\ праворуч)\ праворуч] =\ frac {1} {\ sqrt {\ left (\ frac {3x-2} 5\ праворуч) ^2-1}}\ cdot\ frac35. $$
Множення чисельника і знаменника на$(-1)$ дає:$ \int \frac{1}{x^2-1}\ dx = \int \frac{-1}{1-x^2}\ dx$. Другий інтеграл можна вирішити за допомогою прямого застосування пункту #3 з Key Idea 19, с$a=1$. Таким чином\[ \begin{align} \int \frac{1}{x^2-1}\ dx &= -\int \frac{1}{1-x^2}\ dx \\ &= \left\{\begin{array}{ccc} -\tanh^{-1}\left(x\right)+C & & x^2<1 \\ \\-\coth^{-1}\left(x\right)+C & & 1<x^2 \end{array}\right. \\ &=-\frac12\ln\left|\frac{x+1}{x-1}\right|+C\\ &=\frac12\ln\left|\frac{x-1}{x+1}\right|+C. \end{align}\]
Відзначимо, що саме ця проблема була вирішена на початку розділу 6.5. У цьому прикладі відповідь була дана як$\frac12\ln|x-1|-\frac12\ln|x+1|+C.$ Зауважте, що це еквівалентно відповіді, наведеній у Рівнянні$\PageIndex{29}$, як$\ln(a/b) = \ln a - \ln b$.
Це вимагає заміни, після чого можна застосувати пункт #2 з Key Idea 19.
Нехай$u = 3x$, отже$du = 3dx$. У нас є
\[\int \frac{1}{\sqrt{9x^2+10}}\ dx = \frac13\int\frac{1}{\sqrt{u^2+10}}\ du. \]
Примітка$a^2=10$, отже,$a = \sqrt{10}.$ тепер застосувати інтегральне правило.
\[\begin{align} &= \frac13 \sinh^{-1}\left(\frac{3x}{\sqrt{10}}\right) + C \\&= \frac13 \ln \Big|3x+\sqrt{9x^2+10}\Big|+C. \end{align}\]

Цей розділ охоплює багато землі. Нові функції були введені разом з деякими їх фундаментальними ідентичностями, їх похідними та антипохідними, їх оберненнями та похідними та антипохідними цих інверсів. Було представлено чотири ключові ідеї, кожна з яких містить досить багато інформації.

Не розглядайте цей розділ як містить джерело інформації, яку потрібно запам'ятати, а як орієнтир для майбутнього вирішення проблем. Key Idea 19 містить, мабуть, найкориснішу інформацію. Знайте форми інтеграції, це допомагає оцінити та зрозуміти, як використовувати зворотну гіперболічну відповідь та логарифмічну відповідь.

Наступний розділ робить коротку перерву від демонстрації нових методів інтеграції. Натомість він демонструє техніку оцінки меж, які повертають невизначені форми. Ця методика буде корисна в розділі 6.8, де будуть виникати межі при оцінці певних певних інтегралів.