3.1: Екстремальні значення
- Page ID
- 60699
Наше дослідження обмежень призвело до неперервних функцій, які є певним класом функцій, які поводяться особливо приємно. Обмеження тоді дали нам ще приємніший клас функцій, функцій, які диференційовані.
У цьому розділі досліджуються багато способів, якими ми можемо скористатися інформацією, яку надають безперервні та диференційовані функції.
Враховуючи будь-яку величину, описану функцією, нас часто цікавлять найбільші та/або найменші значення, які досягає кількість. Наприклад, якщо функція описує швидкість об'єкта, здається розумним захотіти знати найшвидший/найповільніший об'єкт, який пройшов. Якщо функція описує вартість акцій, ми можемо знати, як найвищий/найнижчий показник запасу, досягнутий за минулий рік. Ми називаємо такі значення екстремальними значеннями.
Визначення\(\PageIndex{1}\): Minima and Maxima
\(f\)Дозволяти визначатися на інтервалі,\(I\) що містить\(c\).
- \(f(c)\)є мінімальним (також абсолютним мінімумом) від\(f\) on\(I\) if\(f(c) \leq f(x)\) for all\(x\) in\(I\).
- \(f(c)\)є максимумом} (також абсолютним максимумом) від\(f\) on\(I\)\(f(c) \geq f(x)\) if for all\(x\) in\(I\).
Максимальне і мінімальне значення - це крайні значення, або екстремуми,\(f\) вкл\(I\).
Екстремальними значеннями функції є значення\(y\) "", значення, які функція досягає, а не вхідні значення.
Розглянемо Малюнок\(\PageIndex{1}\). Функція, що відображається в (a), має максимум, але не мінімальний, оскільки інтервал, протягом якого визначена функція, відкритий. У (b) функція має мінімум, але не максимум; є розрив у «природному» місці, щоб відбувся максимум. Нарешті, функція, показана в (c), має як максимум, так і мінімум; зверніть увагу, що функція є безперервною, а інтервал, на якому вона визначена, закритий.
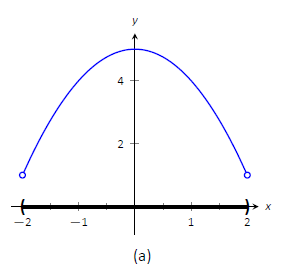
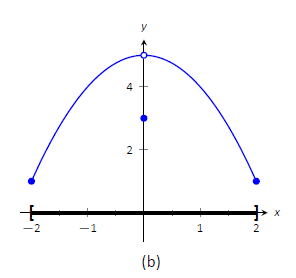
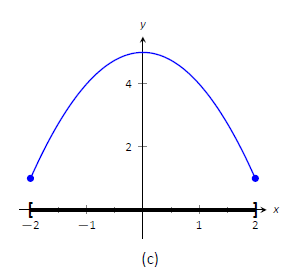
Малюнок\(\PageIndex{1}\): Графіки функцій з екстремальними значеннями і без них
Можна, щоб переривчасті функції, визначені на відкритому інтервалі, мали як максимальне, так і мінімальне значення, але ми щойно бачили приклади, де їх не було. З іншого боку, безперервні функції на замкнутому інтервалі завжди мають максимальне і мінімальне значення.
Теорема\(\PageIndex{1}\): The Extreme Value Theorem
\(f\)Дозволяти неперервна функція, визначена на замкнутому інтервалі\(I\). Потім\(f\) має як максимальне, так і мінімальне значення на\(I\).
Ця теорема стверджує, що\(f\) має екстремальні значення, але вона не дає жодних порад про те, як/де знайти ці значення. Процес може здатися досить легким, як ілюструє наступний приклад. Після прикладу ми будемо спиратися на вивчені уроки, щоб сформувати більш загальний і потужний метод знаходження екстремальних значень.
Приклад\(\PageIndex{1}\): Approximating Extreme Values
Розглянемо\(f(x) = 2x^3-9x^2\) далі\(I=[-1,5]\), як показано на малюнку\(\PageIndex{2}\). Орієнтовні крайні значення\(f\).
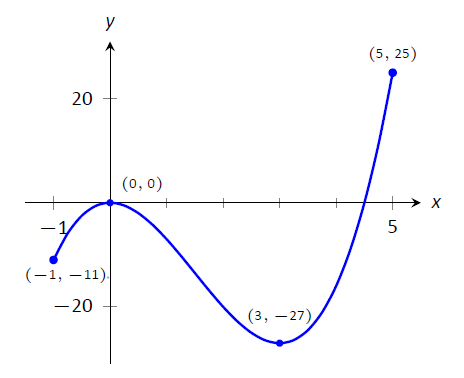
Малюнок\(\PageIndex{2}\): Графік,\(f(x) = 2x^3-9x^2\) як у прикладі\(\PageIndex{1}\)
Рішення
Графік малюється таким чином, щоб привернути увагу до певних моментів. Безумовно, здається, що найменше\(y\) значення є\(-27\), знайдене коли\(x=3\). Також здається, що найбільше\(y\) значення дорівнює 25, знайденому в кінцевій точці\(I\),\(x=5\). Ми використовуємо слово здається, бо лише за графіком ми не можемо бути впевнені, що найменше значення не менше\(-27\). Оскільки задача просить наближення, ми наближаємо крайні значення бути\(25\) і\(-27\).
Зверніть увагу, як мінімальне значення прийшло в «нижній частині пагорба», а максимальне значення прийшло в кінцевій точці. Також зауважте, що хоча\(0\) це не екстремальне значення, було б, якби ми звузили наш інтервал до\([-1,4]\). Ідея про те, що точка\((0,0)\) є місцем розташування екстремального значення для деякого інтервалу, є важливою, що веде нас до визначення.
Локальні та відносні екстреми
Терміни локальний мінімум і локальний максимум часто використовуються як синоніми відносного мінімуму і відносного максимуму. Коротко попрактикуємося використовувати ці визначення.
Визначення\(\PageIndex{2}\): Relative Minimum and Relative Maximum
\(f\)Дозволяти визначатися на інтервалі,\(I\) що містить\(c\).
- Якщо є відкритий інтервал, що містить\(c\) таке, що\(f(c)\) є мінімальним значенням, то\(f(c)\) є відносним мінімумом\(f\). Ми також говоримо, що\(f\) має відносний мінімум при\((c,f(c))\).
- Якщо є відкритий інтервал, що містить\(c\) таке, що\(f(c)\) є максимальним значенням, то\(f(c)\) є відносним максимумом\(f\). Ми також говоримо, що\(f\) має відносний максимум при\((c,f(c))\).
Відносні максимальні та мінімальні значення складають відносні екстремуми\(f\).
Приклад\(\PageIndex{2}\): Approximating Relative Extrema
Розглянемо\(f(x) = (3x^4-4x^3-12x^2+5)/5\), як показано на малюнку\(\PageIndex{3}\). Наближена відносна крайність\(f\). У кожному з цих пунктів оцінюйте\(f'\).
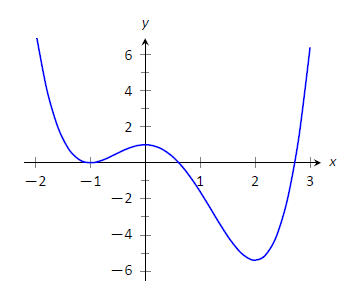
Малюнок\(\PageIndex{3}\): Графік\(f(x) = (3x^4-4x^3-12x^2+5)/5\), як у прикладі\(\PageIndex{2}\).
Рішення
У нас досі немає інструментів для точного пошуку відносних екстремумів, але графік дозволяє нам робити розумні наближення. Здається,\(f\) має відносні мінімуми при\(x=-1\) і\(x=2\), зі значеннями\(f(-1)=0\) і\(f(2) = -5.4\). Також здається, що\(f\) має відносний максимум в точці\((0,1)\).
Ми наближаємо відносні мінімуми бути\(0\) і\(-5.4\); ми наближаємо відносний максимум бути\(1\).
Це просто оцінити\(f'(x) =\frac15(12x^3-12x^2-24x)\) в\(x=0, 1\) і\(2\). У кожному конкретному випадку,\(f'(x) = 0\).
Приклад\(\PageIndex{3}\): Approximating Relative Extrema
Приблизна відносна крайність\(f(x) = (x-1)^{2/3}+2\), показана на рис\(\PageIndex{4}\). У кожному з цих пунктів оцінюйте\(f'\).
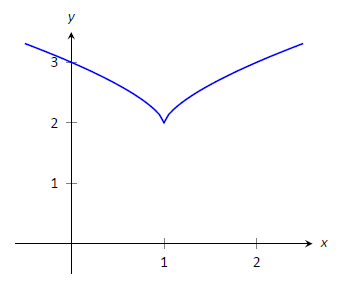
Малюнок\(\PageIndex{4}\): Графік\(f(x) = (x-1)^{2/3}+2\), як у прикладі\(\PageIndex{3}\).
Рішення
Цифра має на увазі, що\(f\) не має ніяких відносних максимумів, але має відносний мінімум при\((1,2)\). Насправді графік говорить про те, що не тільки ця точка є відносним мінімумом,\(y=f(1)=2\) мінімальним значенням функції.
Обчислюємо\(f'(x) = \frac{2}{3}(x-1)^{-1/3}\). Коли\(x=1\),\(f'\) не визначено.
Що ми можемо дізнатися з попередніх двох прикладів? Ми змогли візуально наблизити відносну крайність, і в кожній такій точці похідна була\(0\) або або вона не була визначена. Це спостереження стосується всіх функцій, що призводить до визначення та теореми.
Визначення\(\PageIndex{3}\): Critical Numbers and Critical Points
\(f\)Дозволяти визначатися в\(c\). Значення\(c\) є критичним числом (або критичним значенням)\(f\) якщо\(f'(c)=0\) або\(f'(c)\) не визначено.
Якщо\(c\) критичне число\(f\), то точка\((c,f(c))\) є критичною точкою\(f\).
Теорема\(\PageIndex{1}\): Relative Extrema and Critical Points
Нехай функція\(f\) має відносну крайність в точці\((c,f(c))\). Потім\(c\) йде критичне число\(f\).
Будьте обережні, щоб зрозуміти, що ця теорема говорить: «Всі відносні крайності відбуваються в критичних точках». У ньому не сказано: «Всі критичні числа виробляють відносну крайність». Наприклад, розгляньте\(f(x) = x^3\). Так як\(f'(x) = 3x^2\), це просто визначити, що\(x=0\) є критичним числом\(f\). Однак не\(f\) має відносних крайнощів, як показано на малюнку\(\PageIndex{5}\).
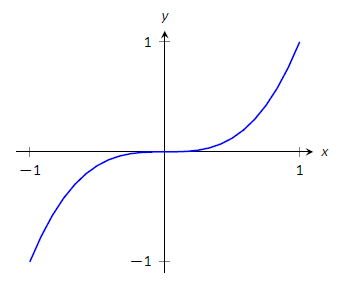
Малюнок\(\PageIndex{5}\): Графік\(f(x)=x^3\) якого має критичне значення\(x=0\), але не відносну крайність.
Теорема\(\PageIndex{1}\) стверджує, що безперервна функція на замкнутому інтервалі матиме абсолютну крайність, тобто як абсолютний максимум, так і абсолютний мінімум. Ці крайності виникають або в кінцевих точках, або при критичних значеннях в інтервалі. Ми поєднуємо ці концепції, щоб запропонувати стратегію пошуку екстрем.
Ключова ідея 2: Пошук екстремуми на замкнутому інтервалі
\(f\)Дозволяти неперервна функція, визначена на замкнутому інтервалі\([a,b]\). Знайти максимальне і мінімальне значення\(f\) на\([a,b]\)
- Оцініть\(f\) в кінцевих точках\(a\) і\(b\) інтервалі.
- Знайдіть критичні числа\(f\) in\([a,b]\).
- Оцінюйте\(f\) при кожному критичному числі.
- \(f\)Абсолютний максимум - найбільша з цих значень, а абсолютний мінімум\(f\) - найменша з цих значень.
Ми практикуємо ці ідеї в наступних прикладах.
Приклад\(\PageIndex{4}\): Finding Extreme Values
Знайдіть крайні значення\(f(x) = 2x^3+3x^2-12x\) on\([0,3]\), зображені на малюнку\(\PageIndex{6}\).
Ми слідуємо крокам, описаним у Key Idea 2. Спочатку оцінюємо\(f\) в кінцевих точках:
\[f(0) = 0 \quad \text{and}\quad f(3) =45.\]
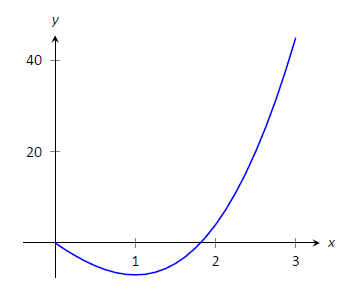
Малюнок\(\PageIndex{6}\): Графік\(f(x) = 2x^3+3x^2-12x\) на\([0,3]\), як у прикладі\(\PageIndex{4}\).
Далі знаходимо критичні значення\(f\) on\([0,3]\). \(f'(x) = 6x^2+6x-12 = 6(x+2)(x-1)\); тому критичні значення\(f\) є\(x=-2\) і\(x=1\). Так як\(x=-2\) не лежить в проміжку\([0,3]\), ми його ігноруємо. Оцінка\(f\) за єдиним критичним числом в нашому інтервалі дає:\(f(1) = -7\).
Таблиця\(\PageIndex{1}\) дає\(f\) оцінені за «важливими»\(x\) значеннями в\([0,3]\). Ми можемо легко побачити максимальне і мінімальне значення\(f\): максимальне значення є\(45\) і мінімальне значення є\(-7\).
| \(x\) | \(f(x)\) |
|---|---|
| \ (x\) ">0 | \ (f (x)\) ">0 |
| \ (x\) ">1 | \ (f (x)\) ">-7 |
| \ (x\) ">3 | \ (f (x)\) ">45 |
Зауважте, що все це було зроблено без допомоги графіка; ця робота слідувала аналітичному алгоритму і не залежала від будь-якої візуалізації. Малюнок\(\PageIndex{6}\) показує\(f\) і ми можемо підтвердити свою відповідь, але важливо розуміти, що ці відповіді можна знайти без графічної допомоги.
Знову практикуємося.
Приклад\(\PageIndex{5}\): Finding Extreme Values
Знайти максимальне і мінімальне значення\(f\) on\([-4,2]\), де
\[f(x) = \left\{\begin{array}{cc} (x-1)^2 & x\leq 0 \\ x+1 & x>0 \end{array}\right. .\]
Рішення
\(f\)Ось фрагментарно визначено, але ми все ще можемо застосувати Ключ Ідея 2. Оцінка\(f\) в кінцевих точках дає:
\[ f(-4) = 25 \quad \text{and} \quad f(2) = 3.\]
Тепер ми знаходимо критичні цифри\(f\). Ми повинні визначити\(f'\) по кусковому порядку; це
\[f'(x) =\left\{\begin{array}{cc} 2(x-1) & x < 0 \\ 1 & x>0 \end{array}\right. .\]
Зверніть увагу, що while\(f\) визначається для всіх\([-4,2]\), не\(f'\) є, оскільки похідна від\(f\) не існує, коли\(x=0\). (Зліва наближається похідна\(-2\); праворуч похідна - 1.) Таким чином, одним критичним числом\(f\) є\(x=0\).
Ми тепер встановили\(f'(x) = 0\). Коли\(x >0\), ніколи не\(f'(x)\) дорівнює 0. Коли\(x<0\),\(f'(x)\) також ніколи не дорівнює 0. (Ми можемо спокуситися сказати, що\(f'(x) = 0 \) коли\(x=1\). Однак це безглуздо, бо ми враховуємо лише\(f'(x) = 2(x-1)\) коли\(x<0\), тому ми будемо ігнорувати рішення, яке говорить\(x=1\).)
Отже, ми маємо три важливі\(x\) значення, які слід враховувати:\(x= -4, 2\) і\(0\). Оцінка\(f\) у кожного дає, відповідно,\(3\) і\(25\)\(1\), наведено в табл\(\PageIndex{2}\). Таким чином, абсолютний мінімум\(f\) дорівнює 1; абсолютний максимум\(f\) є\(25\). Наша відповідь підтверджується графіком\(f\) на рис\(\PageIndex{7}\).
| \(x\) | \(f(x)\) |
| -4 | 25 |
| 0 | 1 |
| 2 | 3 |
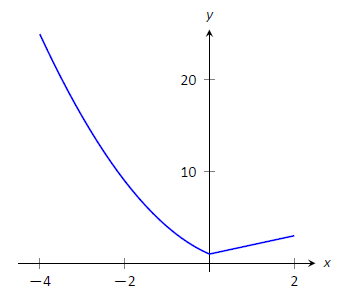
Малюнок\(\PageIndex{7}\): Графік\(f(x)\) на\([-4,2]\), як у прикладі\(\PageIndex{5}\).
Приклад\(\PageIndex{6}\): Finding Extreme Values
Знайдіть крайність\(f(x) = \cos (x^2)\) на\([-2,2]\).
Рішення
Ми знову використовуємо Key Idea 3. Оцінка\(f\) в кінцевих точках інтервалу дає: Тепер\(f(-2) = f(2) = \cos (4) \approx -0.6536.\) ми знаходимо критичні значення\(f\).
Застосовуючи правило ланцюга, знаходимо\(f'(x) = -2x\sin (x^2)\). Встановіть\(f'(x) = 0\) і вирішуйте\(x\) для пошуку критичних значень\(f\).
У нас є\(f'(x) = 0\) коли\(x = 0\) і коли\(\sin (x^2) = 0\). Загалом,\(\sin t = 0\) коли\(t = \ldots -2\pi, -\pi, 0, \pi, \ldots\) Таким чином,\(\sin (x^2) = 0\) коли\(x^2 = 0, \pi, 2\pi, \ldots\) (\(x^2\)завжди позитивно\(-\pi\), тому ми ігноруємо тощо) Так\(\sin (x^2)=0\) коли\(x= 0, \pm \sqrt{\pi}, \pm\sqrt{2\pi}, \ldots\). Єдині значення, що потрапляють у заданий інтервал,\([-2,2]\) є\(-\sqrt{\pi}\) і\(\sqrt{\pi}\), приблизно\(\pm 1.77\).
Ми знову будуємо таблицю важливих значень в табл\(\PageIndex{3}\). У цьому прикладі ми маємо 5 значень для розгляду:\(x= 0, \pm 2, \pm\sqrt{\pi}\).
| \(x\) | \(f(x)\) |
|---|---|
| \ (x\) ">-2 | \ (f (x)\) ">-0,65 |
| \ (x\) ">\(-\sqrt{\pi}\) | \ (f (x)\) ">-1 |
| \ (x\) ">0 | \ (f (x)\) ">1 |
| \ (x\) ">\(\sqrt{\pi}\) | \ (f (x)\) ">-1 |
| \ (x\) ">2 | \ (f (x)\) ">-0,65 |
З таблиці видно, що максимальне значення\(f\) включення\([-2,2]\) дорівнює 1; мінімальне значення -\(-1\). Графік на малюнку\(\PageIndex{8}\) підтверджує наші результати.
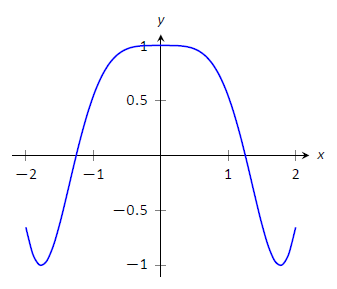
Малюнок\(\PageIndex{8}\): Графік\(f(x)=\cos(x^2)\) на\([-2,2]\), як у прикладі\(\PageIndex{5}\).
Розглянемо ще один приклад.
Приклад\(\PageIndex{7}\): Finding Extreme Values
Знайдіть крайні значення\(f(x) = \sqrt{1-x^2}\).
Рішення
Замкнутий інтервал не задано, тому знаходимо крайні значення\(f\) на його області. \(f\)визначається всякий раз\(1-x^2\geq 0\); таким чином домен\(f\) є\([-1,1]\). Оцінювання\(f\) в будь-якій кінцевій точці повертає\(0\).
Використовуючи правило ланцюга, знаходимо\(f'(x) = \frac{-x}{\sqrt{1-x^2}}\). Критичні точки\(f\) знаходять, коли\(f'(x) = 0\) або коли\(f'\) не визначено. Це просто знайти, що\(f'(x) = 0\) коли\(x=0\), і\(f'\) не визначено\(x=\pm 1\), коли, кінцеві точки інтервалу. Таблиця важливих значень наведена в табл\(\PageIndex{4}\).
| \(x\) | \(f(x)\) |
|---|---|
| \ (x\) ">-1 | \ (f (x)\) ">0 |
| \ (x\) ">0 | \ (f (x)\) ">1 |
| \ (x\) ">1 | \ (f (x)\) ">0 |
Максимальне значення дорівнює 1, а мінімальне - 0.
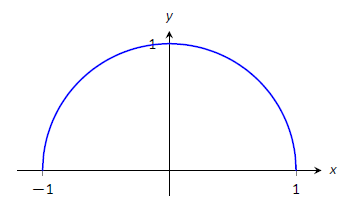
Малюнок\(\PageIndex{9}\): Графік\(f(x)=\sqrt{1-x^2}\) увімкнення\([-1,1]\), як у прикладі\(\PageIndex{7}\)
Примітка: Ми неявно знайшли похідну\(x^2+y^2=1\) одиничного кола в розділі про неявну диференціацію як\(\frac{dy}{dx} = -x/y\). У\(\PageIndex{7}\) прикладі половина одиничного кола задається як\(y=f(x) = \sqrt{1-x^2}\). Ми знайшли\(f'(x) = \frac{-x}{\sqrt{1-x^2}}\). Визнайте, що знаменник цього дробу є\(y\); тобто ми знову знайшли\(f'(x) = \frac{dy}{dx} = -x/y.\)
Ми бачили, що безперервні функції на замкнутих інтервалах завжди мають максимальне та мінімальне значення, і ми також розробили методику пошуку цих значень. У наступному розділі ми продовжимо наше вивчення інформації, яку ми можемо отримати з «приємних» функцій з теоремою про середнє значення. На замкнутому інтервалі ми можемо знайти середню швидкість зміни функції (як ми це робили на початку глави 2). Ми побачимо, що диференційовані функції завжди мають точку, в якій їх миттєва швидкість зміни така ж, як середня швидкість зміни. Це дивно корисно, як ми побачимо.
