1.2: Від'ємні числа

Негативні цифри - це факт життя, від зимових температур до наших банківських рахунків. Давайте потренуємося оцінювати вирази, що включають негативні числа.

Абсолютна величина

Абсолютна величина числа - це його відстань від$0$. Ви можете думати про це як розмір числа, не ідентифікуючи його як позитивний чи негативний. Числа з однаковим абсолютним значенням, але різними знаками, такими як$3$ і$-3$, називаються протилежностями. Абсолютне значення$-3$ є$3$, і абсолютне значення також$3$ є$3$.

Ми використовуємо пару прямих вертикальних смуг для позначення абсолютного значення; наприклад,$|-3|=3$ і$|3|=3$.

Вправи$\PageIndex{1}$

Оцініть кожен вираз.

1. $|-5|$

2. $|5|$

Відповідь

1. 5

2. 5

Додавання негативних чисел

Щоб додати два негативних числа, додайте їх абсолютні значення (тобто ігноруйте негативні знаки) і зробіть остаточну відповідь негативною.

Вправи$\PageIndex{1}$

Виконайте кожне додавання.

3. $-8+(-7)$

4. $-13+(-9)$

Відповідь

3. -15

4. -22

Щоб додати додатне число і від'ємне число, віднімаємо меншу абсолютну величину від більшого. Якщо додатне число має більшу абсолютну величину, остаточна відповідь позитивна. Якщо від'ємне число має більшу абсолютну величину, остаточна відповідь негативна.

Вправи$\PageIndex{1}$

Виконайте кожне додавання.

5. $7+(-3)$

6. $-7+3$

7. $14+(-23)$

8. $-14+23$

9. Температура опівдні в прохолодний понеділок була$-7$ °F До наступного дня опівдні піднялася$25$ °F Яка температура опівдні у вівторок?

Відповідь

5. 4

6. -4

7. -9

8. 9

9. $18$°F

Якщо вираз складається тільки з доповнень, ми можемо порушити правила порядку операцій і додати числа в будь-якому порядку, який ми вибрали.

Вправи$\PageIndex{1}$

Оцінюйте кожен вираз за допомогою будь-яких ярликів, які ви помітили.

10. $-10+4+(-4)+3+10$

11. $-291+73+(-9)+27$

Відповідь

10. $3$

11. -200

Віднімання від'ємних чисел

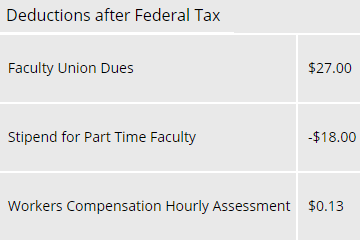
На зображенні нижче показана частина paystub, в якій потрібно було здійснити$18$ платіж $, але люди з нарахування заробітної плати хотіли відстежувати платіж у категорії відрахувань. Звичайно, позитивне число у відрахуваннях буде віднімати гроші з зарплати. Однак тут відрахування негативних$18$ доларів має ефект додавання$18$ доларів до зарплати. Віднімання негативної суми еквівалентно додаванню позитивної суми.

Щоб відняти два знакових числа, додаємо перше число до протилежного другому числу.

Вправи$\PageIndex{1}$

Виконайте кожне віднімання.

12. $5-2$

13. $2-5$

14. $-2-5$

15. $-5-2$

16. $2-(-5)$

17. $5-(-2)$

18. $-2-(-5)$

19. $-5-(-2)$

20. Одного дня в лютому температура в Портленді, штат Орегон$43$ °F, а температура в Портленді, штат Мен -$-12$ °F.

Відповідь

12. 3

13. -3

14. -7

15. -7

16. 7

17. 7

18. 3

19. -3

20. $55$Різниця° F

Множення від'ємних чисел

Припустимо, ви витрачаєте$3$ долари на каву щодня. Ми могли б представляти витрачати 3 долари як негативне число,$-3$ долари. Протягом робочого тижня$5$ -день, ви б витратили$15$ долари, які ми могли б представляти як$-15$ долари. Це показує$-3\cdot5=-15$, що, або$5\cdot-3=-15$.

Якщо перемножити два числа з протилежними знаками, твір негативне.

Вправа$\PageIndex{1}$

Знайдіть кожен товар.

21. $-4\cdot3$

22. $5(-8)$

Відповідь

21. -12

22. -40

Повертаючись до нашого кавового прикладу, ми побачили це$5(-3)=-15$. Тому протилежне$5(-3)$ має бути позитивним$15$. Тому$-5$ що протилежне$5$, це означає, що$-5(-3)=15$.

Якщо перемножити два числа з однаковим знаком, твір позитивний.

УВАГА! Ці правила відрізняються від правил додавання; будьте обережні, щоб не переплутати їх.

Вправа$\PageIndex{1}$

Знайдіть кожен товар.

23. $-2(-9)$

24. $-3(-7)$

Відповідь

23. 18

24. 21

Нагадаємо, що показник являє собою повторне множення. Давайте подивимося, що відбувається, коли ми піднімаємо негативне число до показника.

Вправи$\PageIndex{1}$

Оцініть кожен вираз.

25. $(-2)^2$

26. $(-2)^3$

27. $(-2)^4$

28. $(-2)^5$

Відповідь

25. $4$

26. -8

27. 16

28. -32

Якщо негативне число підвищується до непарної, результат буде негативним.
Якщо негативне число підвищується до парної потужності, результат позитивний.

Ділення від'ємних чисел

Повернемося до прикладу кави, який ми бачили раніше:$-3\cdot5=-15$. Ми можемо переписати цей факт за допомогою ділення і побачити, що$-15\div5=-3$; негатив, розділений на позитив, дає негативний результат. Також$-15\div-3=5$; негатив, розділений на негатив, дає позитивний результат. Це означає, що правила ділення працюють точно так само, як і правила множення.

Якщо розділити два числа з протилежними знаками, частка негативна.
Якщо розділити два числа з однаковим знаком, частка позитивна.

Вправи$\PageIndex{1}$

Знайдіть кожен коефіцієнт.

29. $-42\div6$

30. $32\div(-8)$

31. $-27\div(-3)$

32. $0\div4$

33. $0\div(-4)$

34. $4\div0$

Відповідь

29. -7

30. -4

31. 9

32. 0

33. 0

34. невизначений

Продовжуйте і перевірте ці останні три вправи за допомогою калькулятора. Будь-які сюрпризи?

• 0 ділиться на інше число - 0.
• Число, поділене на 0, є невизначеною, або не дійсним числом.

Ось коротке пояснення того, чому не$4\div0$ може бути дійсним числом. Припустимо, що є таємничий номер, який ми будемо називати$n$, такий що$4\div0=n$. Тоді ми можемо переписати це ділення як пов'язане множення,$n\cdot0=4$. Але тому, що$0$ раз будь-яке число$0$, ліва сторона цього рівняння$0$, і ми отримуємо результат$0=4$, що, який не має сенсу. Тому такого числа немає$n$, і$4\div0$ не може бути дійсним числом.

Порядок операцій з від'ємними числами

П: Працюйте всередині дужок або угруповання символів, дотримуючись порядку PEMDAS у міру необхідності.

E: Оцініть показники.

MD: Виконуйте множення і ділення зліва направо.

AS: Виконуйте додавання і віднімання зліва направо.

Давайте закінчимо цей модуль певним порядком практики операцій.

Вправи$\PageIndex{1}$

Оцінити кожен вираз, використовуючи порядок операцій.

35. $(2-5)^2\cdot2+1$

36. $2-5^2\cdot(2+1)$

37. $[7(-2)+16]\div2$

38. $7(-2)+16\div2$

39. $\dfrac{1-3^4}{2(5)}$

40. $\dfrac{(1-3)^4}{2}\cdot5$

Відповідь

35. $19$

36. -73

37. 1

38. -6

39. -8

40. 40