Skip to main content
LibreTexts - Ukrayinska

1.1: Порядок операцій

  1. Last updated
  2. Save as PDF
  • Page ID
    65890

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Оцінити вираз означає спростити його і знайти його значення.

    Вправи\(\PageIndex{1}\)

    1. Оцініть, виконавши додавання спочатку:\(12-2+3\)

    2. Оцініть, виконавши спочатку віднімання:\(12-2+3\)

    Відповідь

    1. 7

    2. 13

    Коли ми оцінюємо вираз, ми хочемо мати одну правильну відповідь. Це не дуже корисно, щоб відповідь була «може бути 7, або, можливо, 13». Математики визначилися з порядком операцій, який говорить нам, які кроки слід зробити перед іншими кроками. Думайте про них як про правила дорожнього руху.

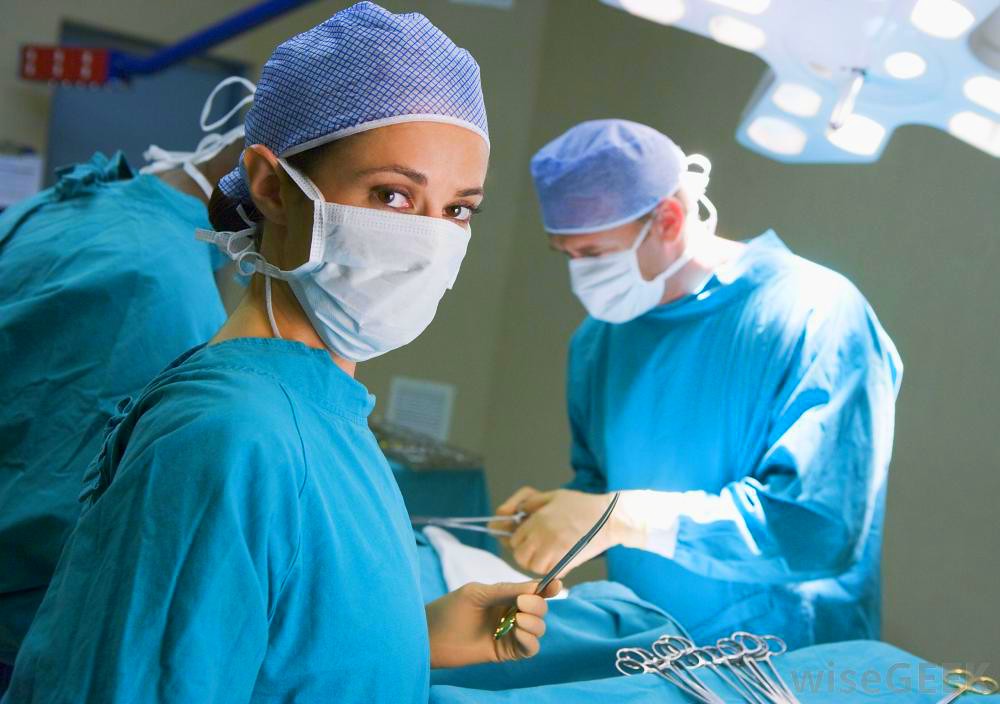
    Порядок операцій: PEMDAS

    П: Працюйте всередині дужок або угруповання символів, дотримуючись порядку PEMDAS, якщо це необхідно всередині символів групування.

    E: Оцініть показники.

    MD: Виконуйте множення і ділення зліва направо.

    AS: Виконуйте додавання і віднімання зліва направо.

    Вправи\(\PageIndex{1}\)

    3. \(12-(2+3)\)

    4. \(12-2+3\)

    Відповідь

    3. 7

    4. 13

    На основі вправ 3 та 4 ми бачимо, що Вправа 1 сказала нам використовувати неправильний порядок операцій. Якщо дужок немає, ми повинні оцінити\(12-2+3\), спочатку виконавши віднімання, а потім виконавши додавання.

    Перш ніж ми рухатися далі, ви повинні знати, що існує кілька способів показати множення. Всі перераховані нижче представляють\(3\times4\):

    \(3\cdot4\)\(3*4\)\(3(4)\)\((3)4\)\((3)(4)\)

    У цьому підручнику ви найчастіше будете бачити крапку, лайк\(3\cdot4\), або дужки безпосередньо поруч з числом, на кшталт\(3(4)\). Ми схильні уникати використання\(3\times4\) символу, оскільки його можна прийняти за букву х.

    Вправи\(\PageIndex{1}\)

    Спрощуйте кожен вираз.

    5. \(12\div(3\cdot2)\)

    6. \(12\div3\cdot2\)

    7. \(5(1+3)-2\)

    8. \(5(1)+(3-2)\)

    Відповідь

    5. 2

    6. 8

    7. 18

    8. 6

    Показник вказує на повторне множення. Наприклад,\(6^2=6\cdot6=36\) і\(4^3=4\cdot4\cdot4=64\). Показник показує нам, скільки факторів бази множаться разом.

    Вправи\(\PageIndex{1}\)

    Спрощуйте кожен вираз.

    9. \(3^2+4^2\)

    10. \((3 + 4)^2\)

    11. \((7+3)(7-5)^3\)

    12. \(7+3(7-5)^3\)

    Відповідь

    9. 25

    10. 49

    11. 80

    12. 31

    У наступному комплексі вправ єдиними відмінностями є дужки, але кожна вправа має різну відповідь.

    Вправи\(\PageIndex{1}\)

    Спрощуйте кожен вираз.

    13. \(39-7\cdot2+3\)

    14. \((39-7)\cdot2+3\)

    15. \(39-(7\cdot2+3)\)

    16. \(39-7\cdot(2+3)\)

    17. \((39-7)\cdot(2+3)\)

    Відповідь

    13. 28

    14. 67

    15. 22

    16. 4

    17. 160

    Можна мати символи групування, вкладені в символи групування; наприклад,\(7+(5^2-(3(17-12\div4)+2\cdot5)\div4)\).

    Щоб дещо полегшити збіг пар лівої та правої дужок, ми можемо використовувати квадратні дужки замість:\(7+(5^2-[3(17-12\div4)+2\cdot5]\div4)\).

    Вправи\(\PageIndex{1}\)

    Спростити вираз.

    18. \(7+(5^2-[3(17-12\div4)+2\cdot5]\div4)\)

    Відповідь

    18. 19

    Рядок дробу - це ще один символ групування; він говорить нам виконати всі кроки вгорі та окремо виконати всі кроки нижче. Завершальним кроком є поділ верхнього числа на нижнє число.

    Вправи\(\PageIndex{1}\)

    Спрощуйте кожен вираз.

    19. \(\dfrac{15-1}{6+1}\)

    20. \(\dfrac{(7+2)\cdot4}{18\div(3+3)}\)

    21. \(\dfrac{5\cdot4^2}{2}\)

    22. \(\dfrac{(5\cdot4)^2}{2}\)

    23. \(\dfrac{(5 - 1)^2}{2+6}\)

    24. \((5 - 1)^2\div2+6\)

    Відповідь

    19. 2

    20. 12

    21. 40

    22. 200

    23. 2

    24. 14

    Ми розглянемо формули в більш пізньому модулі, але давайте закінчимо перекладом зі слів на математичний вираз.

    Вправи\(\PageIndex{1}\)

    25. Ви можете знайти приблизну температуру за Фаренгейтом, подвоївши температуру за Цельсієм і додаючи\(30\). Якщо температура становить\(9\) °C, яка приблизна температура за Фаренгейтом? Напишіть вираз і спростіть його.

    26. Ви можете знайти приблизну температуру за Цельсієм, віднімаючи\(30\) від температури Фаренгейта, а потім розділивши на\(2\). Якщо температура становить\(72\)° F, яка приблизна температура за Цельсієм? Напишіть вираз і спростіть його.

    Відповідь

    25. \(9\cdot2+30=48\)°F

    26. \((72-30)\div2=21\)°C