9.2: Раціональні числа
- Page ID
- 67001
Матеріали: Дробні кола, фракційні масиви, кілька смужок, С-смужки
Використовуйте свої позначені кола дробу, щоб зробити ці перші кілька дій.
Візьміть по одному клину з кожного кола фракції (1/2, 1/3, 1/4, 1/5, 1/6, 1/8, 1/9, 1/10 і 1/12). Одна фракція більша за іншу, якщо вона охоплює більше місця, ніж інша. Порівняйте їх і наведіть порядок від найменшого до найбільшого, і запишіть їх в порядку нижче, використовуючи символ менше ніж (<).
З того, що ви виявили у вправі 1, обведіть більшу частку в кожному випадку.
| а. 1/90 або 1/95 | б. 1/32 або 1/33 |
Якщо взяти 5 шматочків фракції, які говорять 1/8, то разом у вас 5/8. Використовуйте цей факт для виконання наступної вправи.
Використовуйте кола дробів для порівняння 5/6, 5/8, 5/9, 5/10 та 5/12. Помістіть їх у порядку від найменшого до найбільшого, використовуючи символ менше ніж (<).
З того, що ви виявили у вправі 3, обведіть більшу частку в кожному випадку.
| а. 15/37 або 15/40 | б. 89/100 або 89/200 |
Використовуйте масив дробів для впорядкування цих дробів: 4/5, 4/6, 4/7, 4/8, 4/9, 4/10, 4/11 та 4/12. Помістіть їх у порядку від найменшого до найбільшого, використовуючи символ менше ніж (<).
Поясніть шаблон, який ви дізналися, виконуючи вправи 1-5.
Використовуйте кола дробів для порівняння цих дробів: 1/2, 2/3, 3/4, 4/5, 5/6, 7/8, 8/9, 9/10 та 11/12. Помістіть їх у порядку від найменшого до найбільшого, використовуючи символ менше ніж (<).
Використовуйте масив дробів для впорядкування цих дробів: 1/2, 2/3, 3/4, 4/5, 5/6, 7/8, 8/9, 9/10, 11/12. Помістіть їх у порядку від найменшого до найбільшого, використовуючи символ менше ніж (<).
З того, що ви виявили у вправах 7 і 8, обведіть більшу частку в кожному випадку.
| а. 89/90 або 94/95 | б. 56/57 або 31/33 |
Порядок цих дробів: 45/46, 71/72, 34/35, 99/100, 25/26, 13/14, 51/52. Помістіть їх у порядку від найменшого до найбільшого, використовуючи символ менше ніж (<).
Поясніть схему, яку ви дізналися з виконання вправ 7 - 10.
Намалюйте власну модель, яка допомогла б переконати когось, чому 4/5 був більше 2/3.
Раціональне число - це просто формальна назва дробу. Нижче наведено формальне визначення раціонального числа.
Раціональне число - це число, яке може бути записано як частка (відношення) цілого числа\(m\), і ненульове ціле число\(n\), яке записується так:\(\frac{m}{n}\).
При написанні в такому вигляді,\(m\) називається чисельником і\(n\) називається знаменником. Якщо GCF (\(m,n\)) = 1 (тобто\(m\) і не\(n\) мають спільних факторів), то про раціональне число говорять в найпростішому (або зменшеному) вигляді.
Нижче наведено один із способів представлення раціонального числа,\(\frac{m}{n}\).
Розділіть (визначену) одиницю на рівну кількість\(n\) частин або підмножин. А значить,\(n\) деталі складають ціле. Кожна з цих частин (або підмножин) представляє\(\frac{1}{n}\). Потім,\(m\) з цих частин представляє\(\frac{m}{n}\).
Для кожного раціонального числа\(\frac{m}{n}\),
- Визначте одиницю в терміні точок. Вкажіть значення кожної точки.
- Розділіть одиницю на рівне число (знаменник) частин.
- Показувати представлення\(\frac{1}{n}\).
- Показувати представлення\(\frac{m}{n}\).
- Визначте одиницю по-іншому, і виконайте три частини (i, ii та iii) ще раз.
|
а Нехай одна одиниця буде визначена 8 крапками, як показано нижче. Кожна точка = 1/8 \[\begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] i. одиниця розділена на 8 рівних частин, як показано нижче.  II. Нижче наведено подання 1/8, що є однією з рівних частин, показаних у частині b. \[\boldsymbol{\cdot}\nonumber \] III.Нижче наведено подання 3/8. \[\begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] |
b Нехай одна одиниця буде визначена 16 крапками, як показано нижче. Кожна точка = 1/16 \[\begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] i. одиниця розділена на 8 рівних частин, як показано нижче. 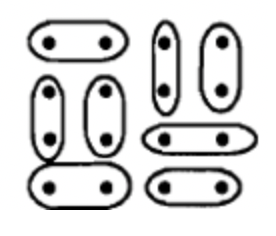 II. Нижче наведено подання 1/8, що є однією з рівних частин, показаних у частині b. \[\begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] III.Нижче наведено подання 3/8. \[\begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] |
Зверніть увагу, що є 3 точки для відповіді в частині a, де кожна точка представляє 1/8. Отже, 3 точки представляють собою число 3/8. Для частини b відповідь має 6 точок. Оскільки кожна точка представляє 1/16, це також представляє 6/16. Тому 3/8 і 6/16 повинні представляти одне і те ж число. Два дроби, що представляють одне і те ж число, називаються еквівалентними дробами.
Дуже важливо визначити свій блок перед початком будь-якої вправи!
|
а Нехай одна одиниця буде визначена 5 крапками, як показано нижче. Кожна точка = 1/5 \[\begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] i. одиниця розділена на 5 рівних частин, як показано нижче. 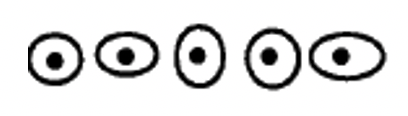 II. Нижче наведено подання 1/5, що є однією з рівних частин, показаних у частині b. \[ \boldsymbol{\cdot} \nonumber \] III.Нижче наведено подання 2/5. \[\begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] |
b Нехай одна одиниця буде визначена 10 крапками, як показано нижче. Кожна точка = 1/10 \[\begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] i. одиниця розділена на 5 рівних частин, як показано нижче. 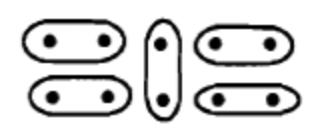 II. Нижче наведено подання 1/5, що є однією з рівних частин, показаних у частині b. \[\begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] III.Нижче наведено подання 2/5 \[\begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] |
Зверніть увагу, що є 2 точки для відповіді в частині a, де кожна точка представляє 1/5. Отже, 2 точки представляють собою число 2/5. Для частини b відповідь має 4 точки. Оскільки кожна точка представляє 1/10, це також представляє 4/10. Тому 2/5 і 4/10 повинні представляти одне і те ж число. Два дроби, що представляють одне і те ж число, називаються еквівалентними дробами.
ДУЖЕ ВАЖЛИВО ВИЗНАЧИТИ СВІЙ БЛОК ПЕРЕД ПОЧАТКОМ БУДЬ-ЯКОЇ ВПРАВИ!
Використовуйте метод в останніх двох прикладах, щоб показати два різних представлення для 3/4.
Використовуйте масиви дробів для визначення всіх дробів у масиві дробів, еквівалентних 1/2. Зробіть це, знайшовши 1/2 на масиві, і побачивши, які інші числа однакової довжини.
Використовуйте масиви дробів для визначення всіх дробів у масиві дробів, еквівалентних 2/3. Зробіть це, знайшовши 2/3 на масиві, і побачивши, які інші числа однакової довжини.
Тепер ви будете використовувати кілька смужок для ідентифікації еквівалентних дробів. Щоб використовувати свої смужки, потрібно вирізати смужки рядами. Щоб знайти дроби, еквівалентні 3/7, вирівняйте смужку 3 над смужкою 7, як показано нижче:
| 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | 33 | 36 |
| 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 | 77 | 84 |
Тепер ви можете побачити одинадцять інших еквівалентних дробів для 3/7:6/14, 9/21, 12/28, 15/35, 18/42, 21/49, 24/56, 27/63, 30/70, 33/77 та 36/84.
Використовуйте кілька смужок, щоб написати 6 дробів, еквівалентних 2/9
Використовуйте кілька смужок, щоб написати 6 дробів, еквівалентних 4/5
Яке правило знаходження дробу, еквівалентного заданому дробу? Наведемо приклад, як знайти деякі дроби, еквівалентні 5/6.
Тепер ми знову працюємо з моделями, використовуючи точки, щоб порівняти два дроби, додати два дроби, відняти два дроби, або помножити або розділити два дроби. Для кожної проблеми важливо, щоб ви починали кожну проблему, прямо вказавши наступне:
1. Будьте конкретні щодо того, що ви використовуєте для пристрою. Найпростіше буде, якщо використовувати масив точок, де знаменником одного дробу є кількість рядків в масиві, а знаменник іншого дробу - кількість стовпців в масиві.
2. Вкажіть значення кожної точки, кожного стовпця та кожного рядка.
Гаразд, перейдемо до прикладу: Використовуйте моделі для порівняння 2/5 та 3/7.
|
Крок 1: Нехай 1 одиниця = 5 рядків точок по 7 стовпців точок, загалом 35 точок, як показано нижче. Оскільки є 35 точок до одиниці, кожна точка = 1/35 одиниці. \[\begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] |
Крок 2: Оскільки рядів 5, одиницю можна розбити на 5 рівних частин, обвівши ряди, як показано нижче: 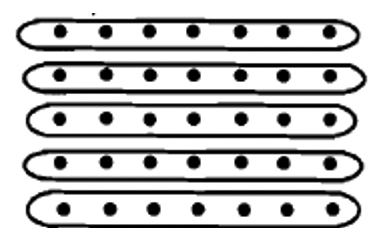 Тому кожен ряд становить 1/5 одиниці. Зверніть увагу, що є 7 точок в 1/5 одиниці: 1/5 =\[ \begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] |
Крок 3: Аналогічно, оскільки є 7 рівних стовпців, кожен стовпець становить 1/7 одиниці: 1/7 =\[ \begin{matrix} \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \end{matrix} \nonumber \] |
|
Крок 4: Тепер, коли ми правильно визначили одиницю, ми готові показати, як виглядає 2/5. Так як 1/5 - це 1 ряд точок, то 2/5 має бути 2 ряди точок. Тому 2/5 показаний нижче: \[ \begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] Зверніть увагу, що 2/5 містить 14 точок, що еквівалентно 14/35. |
Крок 5: Аналогічно, ми можемо показати, як виглядає 3/7. Оскільки 1/7 - це 1 стовпчик точок, то 3/7 має бути 3 стовпчики точок. Тому 3/7 показано нижче: \[ \begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] Зверніть увагу, що 3/7 містить 15 точок, що еквівалентно 15/35. |
Оскільки 2/5 містить менше точок, ніж 3/7, 2/5 має бути менше 3/7. Відповідь: 2/5 < 3/7.
Порівняйте 3/4 і 4/5 за допомогою моделей. Показати всі кроки і пояснити процедуру, як показано в попередньому прикладі.
Гаразд, перейдемо до прикладу додавання: Використовуйте моделі, щоб додати 2/5 та 3/7.
|
Крок 1: Нехай 1 одиниця = 5 рядків точок по 7 стовпців точок, загалом 35 точок, як показано нижче. Оскільки є 35 точок до одиниці, кожна точка = 1/35 одиниці. \[\begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] |
Крок 2: Оскільки рядів 5, одиницю можна розбити на 5 рівних частин, обвівши ряди, як показано нижче:  Тому кожен ряд становить 1/5 одиниці. Зверніть увагу, що є 7 точок в 1/5 одиниці: 1/5 =\[ \begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] |
Крок 3: Аналогічно, оскільки є 7 рівних стовпців, кожен стовпець становить 1/7 одиниці: 1/7 =\[ \begin{matrix} \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \end{matrix} \nonumber \] |
|
Крок 4: Тепер, коли ми правильно визначили одиницю, ми готові показати, як виглядає 2/5. Так як 1/5 - це 1 ряд точок, то 2/5 має бути 2 ряди точок. Тому 2/5 показаний нижче: \[ \begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] Зверніть увагу, що 2/5 містить 14 точок, що еквівалентно 14/35. |
Крок 5: Тепер ми складаємо дві моделі разом, як показано нижче. Відповідь 29/35. \[ \begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] Зверніть увагу, що 3/7 містить 15 точок, що еквівалентно 15/35. |
Крок 5: Тепер ми складаємо дві моделі разом, як показано нижче. Відповідь 29/35.
\[\begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} + \begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} = 29 \text{ dots } = 29/35 \nonumber \]
Додайте 1/4 і 2/5 за допомогою моделей. Показати всі кроки і пояснити процедуру, як показано в попередньому прикладі.
Гаразд, перейдемо до прикладу віднімання: Використовуйте моделі, щоб зробити наступне віднімання: 3/7 - 2/5.
|
Крок 1: Нехай 1 одиниця = 5 рядків точок по 7 стовпців точок, загалом 35 точок, як показано нижче. Оскільки є 35 точок до одиниці, кожна точка = 1/35 одиниці. \[\begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] |
Крок 2: Оскільки рядів 5, одиницю можна розбити на 5 рівних частин, обвівши ряди, як показано нижче:  Тому кожен ряд становить 1/5 одиниці. Зверніть увагу, що є 7 точок в 1/5 одиниці: 1/5 =\[ \begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] |
Крок 3: Аналогічно, оскільки є 7 рівних стовпців, кожен стовпець становить 1/7 одиниці: 1/7 =\[ \begin{matrix} \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \end{matrix} \nonumber \] |
|
Крок 4: Тепер, коли ми правильно визначили одиницю, ми готові показати, як виглядає 2/5. Так як 1/5 - це 1 ряд точок, то 2/5 має бути 2 ряди точок. Тому 2/5 показаний нижче: \[ \begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] Зверніть увагу, що 2/5 містить 14 точок, що еквівалентно 14/35. |
Крок 5: Аналогічно, ми можемо показати, як виглядає 3/7. Оскільки 1/7 - це 1 стовпчик точок, то 3/7 має бути 3 стовпчики точок. Тому 3/7 показано нижче: \[ \begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] Зверніть увагу, що 3/7 містить 15 точок, що еквівалентно 15/35. |
Тепер віднімаємо, як показано нижче. Відповідь 1/35.
\[ \begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} - \begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} = 1 \text{ dot } = 1/35 \nonumber \]
Виконайте наступне віднімання за допомогою моделей: 7/8 — 2/3. Показати всі кроки і пояснити процедуру, як показано в попередньому прикладі.
Множення дробів трохи складніше. Модель повторного додавання не має сенсу при множенні двох дробів. Коли ви бачите дві дроби, помножені разом, як 2/5\(\cdot\) 3/7, подумайте про це як 2/5 З 3/7. Іншими словами, ви повинні взяти 3/7 одиниці, а потім ви повинні взяти 2/5 цього. Зверніть увагу, що ви повинні представляти другий дріб ПЕРЕД тим, як ви можете зробити множення.
Гаразд, перейдемо до прикладу множення: Використовуйте моделі, щоб зробити наступне множення: 2/5\(\cdot\) 3/7.
|
Крок 1: Нехай 1 одиниця = 5 рядків точок по 7 стовпців точок, загалом 35 точок, як показано нижче. Оскільки є 35 точок до одиниці, кожна точка = 1/35 одиниці. \[\begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] |
Крок 2: Оскільки рядів 5, одиницю можна розбити на 5 рівних частин. Тому кожен ряд становить 1/5 одиниці. Зверніть увагу, що є 7 точок в 1/5 одиниці: 1/5 =\[ \begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] |
Крок 3: Аналогічно, оскільки є 7 рівних стовпців, кожен стовпець становить 1/7 одиниці: 1/7 =\[ \begin{matrix} \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \end{matrix} \nonumber \] |
|
Крок 4: Тепер, коли ми правильно визначили одиницю, ми спочатку повинні показати, як виглядає 3/7 (друге число в множенні). Оскільки 1/7 - це 1 стовпчик точок, то 3/7 має бути 3 стовпчики точок. Тому 3/7 показано нижче: \[ \begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] |
Крок 5: Тут є різниця в тому, як ви продовжуєте. Тепер вам потрібно знайти 2/5 з 3/7, що показано на кроці 4. Оскільки на кроці 4 є 5 рядів точок, кожен рядок (з 3 точок) представляє 1/5. Отже, ви хочете лише 2 ряди точок з кроку 4, як показано нижче. \[ \begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] Це відповідь. Є 6 точок, так що це 6/35. |
Множення можна показати все на одній одиниці, спочатку показавши одиницю, друга обводимо частину, яка представляє другий дріб у множенні, а потім обводимо частину, яка представляє перший дріб у множенні. Нижче наведена послідовність кроків для вирішення цієї проблеми.
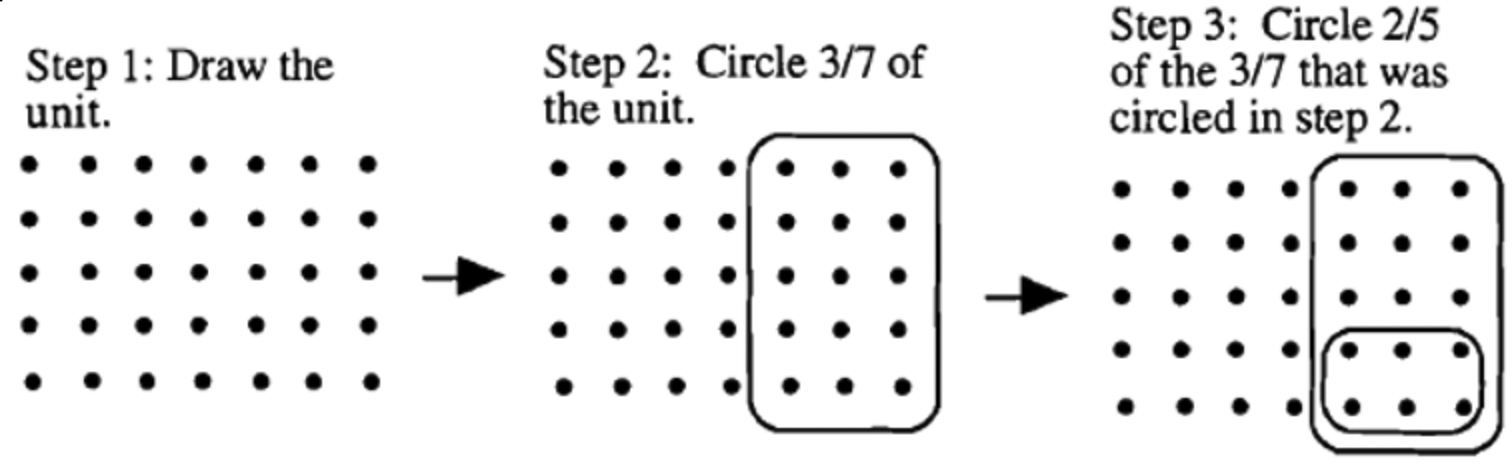
Гаразд, давайте подивимося, як це виглядає, якщо ми переключимо порядок дробів: Використовуйте моделі, щоб зробити наступне множення:\(\bf 3/7 \cdot 2/5\).
|
Крок 1: Нехай 1 одиниця = 5 рядків точок по 7 стовпців точок, загалом 35 точок, як показано нижче. Є 35 точок до одиниці, тому кожна точка = 1/35 одиниці. \[\begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] |
Крок 2: Оскільки рядів 5, одиницю можна розбити на 5 рівних частин. Тому кожен ряд становить 1/5 одиниці. Зверніть увагу, що є 7 точок в 1/5 одиниці: 1/5 =\[ \begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] |
Крок 3: Аналогічно, оскільки є 7 рівних стовпців, кожен стовпець становить 1/7 одиниці: 1/7 =\[ \begin{matrix} \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \end{matrix} \nonumber \] |
|
Крок 4: Тепер, коли ми правильно визначили одиницю, ми спочатку повинні показати, як виглядає 2/5 (друге число в множенні). Оскільки 1/5 - це 1 стовпчик точок, то 2/5 має бути 2 стовпчики точок. Тому 2/5 показаний нижче: \[ \begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] |
Крок 5: Тепер вам потрібно знайти 3/7 з 2/5, що показано на кроці 4. Оскільки на кроці 4 є 7 стовпців крапок, кожен стовпець (з 2 точок) представляє 1/7. Отже, ви хочете лише 3 ряди точок з кроку 4, як показано нижче. \[ \begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \] Це відповідь. Є 6 точок, так що це 6/35. |
Знову ж таки, це множення може бути показано все на одній одиниці, спочатку показавши одиницю, друга обводимо частину, яка представляє другий дріб у множенні, а потім обводимо частину, яка представляє перший дріб у множенні. Нижче наведена послідовність кроків для вирішення цієї проблеми.
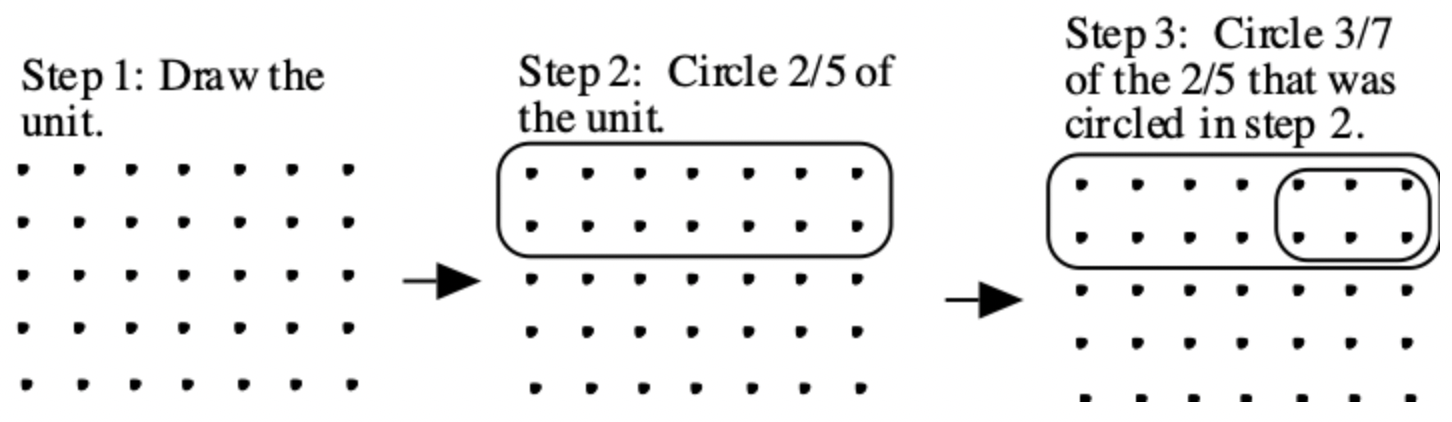
Хоча відповідь однакова для 3/7\(\cdot\) 2/5, і 2/5\(\cdot\) 3/7, послідовність кроків немає. Зверніть увагу на різницю між кроком 3 вище (3/7\(\cdot\) 2/5) та кроком 3 нижче (2/5\(\cdot\) 3/7).
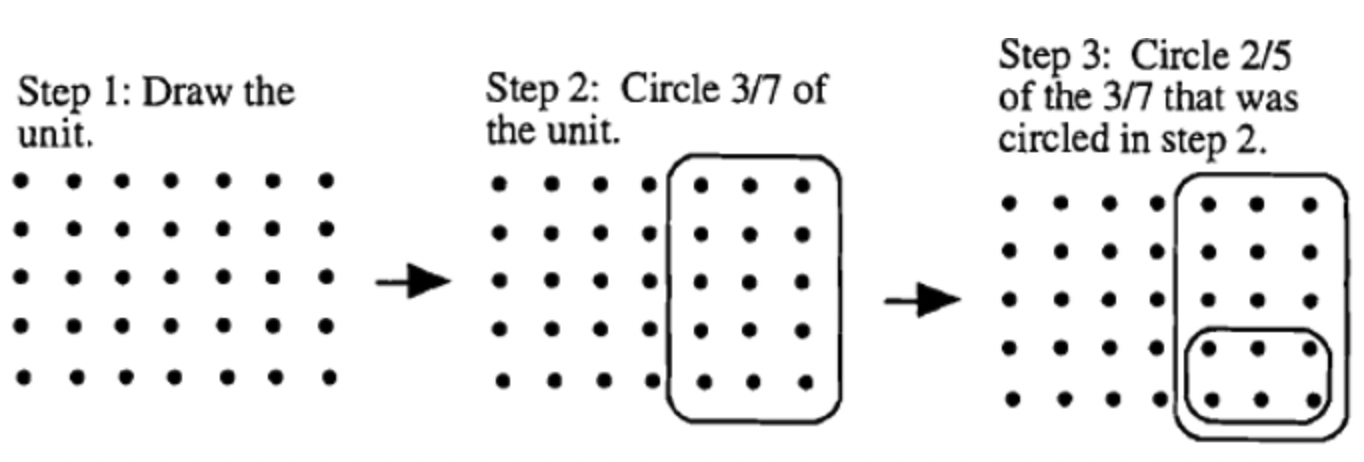
Виконайте наступні множення за допомогою моделей. Показати всі кроки і пояснити процедуру, як показано в попередніх прикладах.
а. 4/5\(\cdot\) 2/3
б. 3/4\(\cdot\) 5/6
Подивившись на остаточний малюнок, хтось змусив змоделювати множення двох дробів, визначити, яке множення було виконано, а потім викласти відповідь. Коло, множення якого представляє правильний вибір.
|
а. 5/6\(\cdot\) 2/3 АБО 2/3\(\cdot\) 5/6 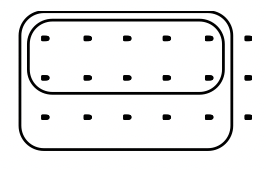 |
б. 1/2\(\cdot\) 7/8 АБО 7/8\(\cdot\) 1/2 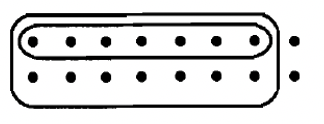 |
Якщо всі точки, показані для кожної задачі, представляють одиницю 1, визначте проблему множення, яку хтось зробив, щоб отримати відповідь, і вкажіть відповідь.
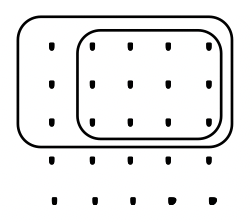 а. а. |
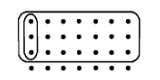 б. б. |
Ще одна модель, яку ви можете використовувати для множення, - це C-смужки, хоча вона дещо обмежує.
Помножити\(3/4 \cdot 1/2\).
Рішення
Це означає 3/4 з 1/2 одиниці. Отже, нам доведеться визначити відповідну одиницю, спочатку взяти 1/2 одиниці, а потім взяти 3/4 відповіді, отриманої після прийняття 1/2. Вибір для 1 одиниці за допомогою C-смуг полягає в тому, щоб помножити знаменники разом, щоб отримати довжину одиничного стрижня, який вам потрібен. У цьому випадку 4\(\cdot\) 2 = 8, тому вибирайте коричневу C-смужку в якості одиниці.
Нехай 1 одиниця = N. Спочатку візьміть 1/2 Браун (N), який є фіолетовим (P). Потім візьміть 3/4 фіолетового кольору, який світло-зелений (L). Відповідь, L, являє собою 3/8, так як одиниця С-смужки була N. Отже, 3/4\(\cdot\) 1/2 = 3/8.
Помножити\(1/2 \cdot 3/4\).
Рішення
Це означає 1/2 з 3/4 одиниці. Отже, нам доведеться визначити відповідну одиницю, спочатку взяти 3/4 одиниці, а потім взяти 1/2 відповіді, отриманої після взяття 3/4. Вибір для 1 одиниці за допомогою C-смуг полягає в тому, щоб помножити знаменники разом, щоб отримати довжину одиничного стрижня, який вам потрібен. У цьому випадку 4\(\cdot\) 2 = 8, тому вибирайте коричневу C-смужку в якості одиниці.
Нехай 1 одиниця = N. Спочатку візьміть 3/4 Браун (N), який є темно-зеленим (D). Потім візьміть 1/42 темно-зеленого (D), який є світло-зеленим (L). Відповідь, L, являє собою 3/8, так як одиниця С-смужки була N. Отже, 1/2\(\cdot\) 3/4 = 3/8.
Помножити\(2/3 \cdot 4/5\).
Рішення
Це означає 2/3 з 4/5 одиниці. Отже, доведеться визначити відповідну одиницю, спочатку взяти 4/5 одиниці, а потім взяти 2/3 відповіді, отриманої після прийняття 4/5. Вибір для 1 одиниці за допомогою C-смуг полягає в тому, щоб помножити знаменники разом, щоб отримати довжину одиничного стрижня, який вам потрібен. В даному випадку 3\(\cdot\) 5 = 15. Існує не одна C-смужка такої довгої, тому використовуйте і помаранчевий+жовтий як одиницю.
Нехай 1 одиниця = O + Y. Спочатку візьміть 4/5 O + Y, який є яскраво-рожевим (H). Потім візьміть 2/3 яскраво-рожевого (Н), який є коричневим (N). Відповідь, N, являє собою 8/15, так як одиниця С-смужки була O + Y. Отже, 2/3\(\cdot\) 4/5 = 8/15.
Скористайтеся C-смужками, щоб помножити 1/3\(\cdot\) 3/4. Поясніть кроки.
Процес виконання множення за допомогою С-смужок можна показати на графіку. Я показав кроки для вищевказаних трьох прикладів на наступній сторінці.
Заповніть діаграму, яка показує, як виконати наступні множення за допомогою C-смужок. Множення знаходиться в першому стовпці. Вкажіть відповідний вибір для одиниці (назвіть C-смужку або суму двох С-смужок) у другому стовпці. Запишіть C-смужку, отриману після першої частини множення (яка є другим дробом у складі одиниці) в третій графі. Потім зробіть остаточне множення, і запишіть отриману С-смужку в четвертому стовпці. У п'ятому стовпці напишіть дріб за допомогою С-смужок, поклавши кінцеву одиницю, отриману в четвертому стовпці в якості чисельника, а одиницю в знаменник. Потім в останньому стовпці напишіть відповідь у вигляді дробу. Не спрощуйте.
| Приклад | \(3/4 \cdot 1/2\) | П | Р | Л | \(\frac{L}{N}\) | \(\frac{3}{8}\) |
| Приклад | \(1/2 \cdot 3/4\) | П | D | Л | \(\frac{L}{N}\) | \(\frac{3}{8}\) |
| Приклад | \(2/3 \cdot 4/5\) | О+У | Ч | П | \(\frac{N}{O+R}\) | \(\frac{8}{15}\) |
| а. | \(1/3 \cdot 3/4\) | |||||
| б. | \(1/2 \cdot 1/4\) | |||||
| c. | \(3/2 \cdot 1/4\) | |||||
| д. | \(2/3 \cdot 1/2\) |
На ділення з раціональними числами...
Пам'ятайте, що відповідь на поділ\(\bf a \div b\) можна отримати, відповівши на це питання: «Скільки множин b міститься в a?»
Давайте використаємо цю ідею, щоб знайти відповідь на таку проблему поділу:
Використовуйте модель для обчислення:\(\bf 3 \div 1/2\)
Рішення
Відповіддю на\(\bf 3 \div 1/2\) це питання є відповіддю: Скільки 1/2 міститься в 3? Нижче наведено два можливі методи, які ви можете використовувати, щоб знайти рішення.
Спосіб 1: Нехай 1 одиниця = 1 квадрат. Потім порахуйте, скільки 1/2 міститься в 3 квадратах.
Намалюйте три квадрата, щоб представити 3. Потім, розділити кожен квадрат на 1/2, порахувати, скільки 1/2 знаходяться в 3 квадратів. З моделі видно, що є 6 1/2 в 3 квадратах. Таким чином, відповідь на 3\(\div\) 1/2 дорівнює 6.
Спосіб 2: Нехай одиниця буде визначена аналогічно тому, як ми це робили для попередніх задач. Помножте знаменники разом, щоб визначити, скільки точок в одиниці. В даному випадку 3 - це те ж саме, що і 3/1. Нехай одиниця = 1 ряд точок на 2 стовпчики точок на загальну суму 2 точки.
Одиниця =\(\begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix}\) Потім представляють число 3 на основі цієї одиниці, і число 1/2 на основі цієї одиниці.
3 = 3 набори по 2 точки =\(\begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix}\) і 1/2 = 1/2 з 2 точок =\(\boldsymbol{\cdot}\)
У множині, що представляє 3, обведіть якомога більше множин, які представляють 1/2:\(\begin{matrix} \boldsymbol{\boxdot} & \boldsymbol{\boxdot} & \boldsymbol{\boxdot} & \boldsymbol{\boxdot} & \boldsymbol{\boxdot} & \boldsymbol{\boxdot} \end{matrix}\)
Підрахуйте, скільки 1/2 знаходяться в 3. Є 6 1/2 в 3, так що відповідь 6.
Спосіб 3: Нехай 1 одиниця = темно-зелена С-смужка. Представляють 3 і 1/2 як C-смужку на основі цієї одиниці. Так як 3 = 3 темно-зелених С-смужки, то 3 = помаранчевий+коричнева С-смужка (або 3 темно-зелені, або яскраво-рожеві + темно-зелені). Так як 1/2 темно-зеленої С-смуги світло-зелена, то 1/2 = світло-зелена С-смужка.
Ми повинні відповісти на питання: Скільки 1/2 в 3? Оскільки 1/2 = L, а 3 = O + N, порахуйте, скільки світло-зелених С-смужок складають довжину O + N С-смужки. Всього їх 6. Знову ж таки, відповідь - 6.
| Одиниця: | D |
|---|
| 3: | Ч | D |
|---|
| 1/2 | Л |
|---|
Ось як отримати відповідь. Покажіть, скільки світлої зелені міститься яскраво-рожевого + темно-зеленого.
| Л | Л | Л | Л | Л | Л |
Зверніть увагу, що ви починаєте з визначення одиниці C-смуги, а потім використовувати цю одиницю для визначення двох чисел у задачі ділення. Але ви НЕ звертаєтеся до одиниці, щоб обчислити проблему поділу. Ви просто порахуєте, скільки дільника (друга С-смужка) знаходиться в дивіденді (перша С-смужка).
Використовуйте модель для обчислення:\(\bf 1/2 \div 1/4\).
Рішення
Відповіддю на\(\bf 1/2 \div 1/4\) це питання є відповіддю: Скільки 1/4 міститься в 1/2?
Нехай 1 одиниця = 2 рядки точок по 4 стовпчики точок:
\[\begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \\ \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} \end{matrix} \nonumber \]
Потім представляємо число 1/2 на основі цієї одиниці, а число 1/4 на основі цієї одиниці.
1/2 =\( \begin{matrix} \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot} & \boldsymbol{\cdot}\end{matrix} \) і 1/4 =\(\begin{matrix} \boldsymbol{\cdot} \\ \boldsymbol{\cdot} \end{matrix}\)
У множині, що представляє 1/2, обведіть якомога більше множин, які представляють 1/4:
Підрахуйте, скільки 1/4 знаходяться в 1/2. Є 2 1/4 в 1/2, так що відповідь 2.
Це також можна зробити за допомогою С-смужок. Нехай одиниця = N. Потім 1/2 = P і 1/4 = R. Так як в фіолетовій С-смужці 2 червоних, 1/2\(\div\) 1/4 = 2.
Використовуйте модель, щоб зробити наступне поділ: 1/5\(\div\) 1/10. Використовуйте коробки, точки або С-смужки. Спочатку визначте одиницю. Потім поясніть і покажіть всі кроки.
Виконайте наступний розподіл за допомогою кожного із способів (коробки, точки, С-смужки):
1/3\(\div\) 1/9. Спочатку визначте одиницю. Потім поясніть і покажіть всі кроки.
Виконайте наступний розподіл за допомогою кожного із способів (коробки, точки, С-смужки):
2/3\(\div\) 1/6. Спочатку визначте одиницю. Потім поясніть і покажіть всі кроки.
Виконайте наступний розподіл за допомогою кожного із способів (коробки, точки, С-смужки):
3\(\div\) 1/4. Спочатку визначте одиницю. Потім поясніть і покажіть всі кроки.
