8.2: Прості та GCF
- Page ID
- 67069
Вам знадобляться: Сантиметрові смужки (Матеріал карти 16A-16L)
Квадрати простих чисел (матеріальні картки 19A-19B)
Складене число квадратів (матеріал карти 20A-20B)
У цих перших кількох вправах ви будете використовувати C-смужки для вивчення дільників, факторів, простих чисел та складених чисел.
а. вийміть гарячу рожеву (H) C-смужку. Використовуйте свої C-смужки (один колір за раз), щоб побачити, чи можете ви сформувати поїзд, складений з С-смужок того ж кольору, рівного по довжині яскраво-рожевій C-смужці іншими словами, подивіться, чи можете ви зробити це з усіма білими (завжди можливо для будь-якої довжини поїзда), або всі червоні, або всі світло-зелені тощо Ви повинні бути в змозі зробити шість різні поїзди кожен поїзд складається з одного кольору. Намалюйте малюнок кожного з цих поїздів під показаним Hot Pink. Я намалював два потяги для вас вже один просто яскраво-рожева смуга (поїзд, що складається всього з однієї C-смуги), а другий складається з трьох фіолетових С-смуг.

б. візьміть кожен шлейф і сформуйте його в прямокутник. Потім знайдіть C-смужку, яка підходить по ширині прямокутника, який є вершиною, якщо C-смужки поїзда, зроблені в прямокутник, розміщені вертикально. З цього ви повинні вміти сказати, з якої проблеми множення утворився кожен поїзд. З цієї інформації напишіть рівняння за допомогою С-смужок, а потім перекладіть в рівняння з числами. Наприклад, для поїзда 2, спочатку я б зробив прямокутник з трьох фіолетових С-смуг. Далі я б спробував знайти C-смужку для розміщення поперек верху, яка була б світло-зеленим. Тому з множення утворився поїзд 2\(L \times P\): пам'ятайте, що оскільки шлейф утворений фіолетовими С-смужками, P - друга буква в множенні. Отже, рівняння в С-смужках є\(L \times P = H\), а числовий еквівалент є\(3 \times 4 = 12\). Дотримуйтесь цієї ж процедури для інших чотирьох поїздів, які ви зробили в частині a.
Поїзд 1 ілюструє множення\(W \times H = H\), або\(1 \times 12 = 12\). (Зверніть увагу, що якщо яскраво-рожева смужка розміщена вертикально, біла С-смужка укладається поперек верху.)
Поїзд 2 ілюструє множення\(L \times P = H\), або\(3 \times 4 = 12\).
Потяг 3 ілюструє множення\(\times\) ____ ____ = H, або ____\(\times\) ____ = 12.
Потяг 4 ілюструє множення\(\times\) ____ ____ = H, або ____\(\times\) ____ = _____
Поїзд 5 ілюструє множення\(\times\) ____ ____ = H, або ____\(\times\) ____ = _____
Поїзд 6 ілюструє множення\(\times\) ____ ____ = H, або ____\(\times\) ____ = _____
У вправі частини 1б набір чисел, розміщених в пробілах перед знаком рівності в рівняннях з числами, називають множниками або дільниками 12. Відзначимо, що через комутативного властивості множення кожен множник або дільник перераховувався двічі.
c Перерахуйте числа, які є факторами 12 (довжина яскраво-рожевої С-смужки). Перерахуйте кожне число лише один раз.
Використовуйте ту саму процедуру, яка використовується у вправі 1, щоб зробити всі можливі прямокутники з поїзда, який має кожну з наступних довжин. Використовуйте C-смужку (и), показані в дужках, щоб зробити поїзд, який має задану довжину. Потім, виявивши можливі прямокутники, які можна зробити, перерахуйте фактори (фактичні числа) кожного числа. Кожне число більше 1 має принаймні два фактори.
| а. фактори 2 (червона С-смужка): ____ |
| б. фактори 3 (світло-зелена С-смужка): ____ |
| c Фактори 4 (фіолетова С-смужка): ____ |
| d Фактори 5 (жовта С-смужка): ____ |
| е Фактори 6 (темно-зелена С-смужка): ____ |
| f Фактори 7 (чорна С-смужка): ____ |
| г Фактори 8 (коричнева С-смужка): ____ |
| h Коефіцієнти 9 (синя С-смужка): ____ |
| i. фактори 10 (помаранчева С-смужка): ____ |
| j Коефіцієнти 11 (срібна С-смужка): ____ |
| k. фактори 13 (коричневий+жовтий): ____ |
| l Фактори 14 (помаранчевий+фіолетовий): ____ |
| м Коефіцієнти 15 (чорний+коричневий): ____ |
| n. коефіцієнти 16 (синій+чорний): ____ |
a. перерахуйте числа з вправи 2, які мають рівно 2 фактори: _____
б Що ви помічаєте про 2 фактори кожного з цих чисел? Чи є закономірність чи щось спільне між собою?
c Перелік номерів з вправи 2, які мають непарне число (3 або 5) множників: _____
d Що спільного у всіх цих чисел?
Означення: Ціле число, яке має рівно два різних множника, називається простим числом.
Якщо число є простим, його єдиними факторами є 1 і саме. Іншими словами, якщо число, p, є простим, його єдиними факторами є 1 і p Якщо ви використовуєте C-смуги і намагаєтеся зробити прямокутник з поїзда, який має довжину, яка є простим числом, єдина можливість полягає в тому, коли ширина дорівнює 1, а довжина - довжина вихідного поїзда. Це тому, що це єдині фактори, і жодне інше число не ділиться на нього.
ПРИМІТКА: 1 НЕ є простим, оскільки він не має двох різних факторів, він має лише один 1.
Означення: Будь-яке ціле число більше 1, яке не є простим, називається складеним числом.
Цілі числа, 0 і 1, не є ні простими, ні складовими. Будь-яке ціле число більше 1 є простим або складеним.
Якщо число є складовим, це означає, що воно має більше 2 факторів, і може бути записано як добуток факторів менше себе. Наприклад, 12 не є простим числом. Він може бути записаний як 2\(\cdot\) 6 або 3\(\cdot\) 4. Це називається факторингом,\(2 \cdots 6\) і\(3 \cdots 4\) є лише двома способами факторингу 12.
Вийдіть з простих чисел квадратів і складених числових квадратів. Якщо ви ще не зробили цього, колір квадратів з простим числом так, що кожне просте число має інший колір 2 може бути жовтим, 3 можуть бути синіми, 5 можуть бути зеленими, 7 можуть бути фіолетовими, 11 можуть бути червоними, 13 можуть бути помаранчевими, 17 можуть бути рожевими, і так далі. Всі складене число квадратів повинні залишитися білими.
Те, що ми збираємося зробити, це множники. Щоразу, коли у нас є біле число, ми знаємо, що воно є складовим і може бути враховано далі. Кінцевою метою буде коефіцієнт чисел у добуток простих чисел, а це означає, що для представлення кожного числа будуть лише кольорові квадрати.
Почнемо з факторингу 12. Вийміть білий квадрат цифри, на якому написано 12, і поставте його перед собою. Оскільки він білий, він може бути врахований у добуток двох менших чисел. Хтось може вибрати 3 і 4; інший може вибрати 2 і 6. Замініть 12 двома квадратами, які ви вибрали. Для 12 трапляється так, що незалежно від того, яку комбінацію двох чисел ви виберете, один із квадратів, який ви виберете, буде кольоровим, а це означає, що він простий і не може бути врахований (або розбитий) далі. А ось інший квадрат буде білим. Замініть білий з двома іншими цифровими квадратами, використовуючи менші коефіцієнти. У вашій купі, замість 12, ви повинні мати три квадрати, 2, а 2 і 3. Немає порядку, це просто група з трьох квадратів, які, якщо помножити разом представляють 12. Нижче наведено два шляхи, які можна було б зробити, щоб придумати остаточне рішення. Стрілки показують один крок за іншим.

На першому шляху, 12 був замінений на 3 і 4, а потім 4 був замінений на два 2, На другому шляху, 12 був замінений на 6 і 2, а потім 6 був замінений на 2 і 3. Використовуючи цю модель для простого множника, числа, які ви в кінцевому підсумку, повинні бути простими, і розуміння полягає в тому, що коли кінцеві (прості) множники множаться разом, ми отримуємо початкове число, яке ми намагалися множити. Іншими словами, просте факторизація для 12 - це\(3 \cdot 2 \cdot 2\). Через комутативних і асоціативних властивостей множення порядок факторів незначний. Іноді для узгодженості фактори пишуться в порядку зростання або спадання, але це не обов'язково, якщо вам не доручено писати його в певному порядку. Якщо вас попросять написати просту факторизацію 12, ви можете написати\(12 = 2 \cdot 2 \cdot 3\) (або\(12 = 2^{2} \cdot 3\)). Щоб перевірити, помножте прості множники, щоб переконатися, що добуток дійсно є числом, яке ви встановили на простий коефіцієнт. Для великих чисел слід скористатися калькулятором. Ось ще один спосіб показати на папері процес заміни відбувається для факторингу 12 за допомогою квадратів числа.

Приклад: Використовуйте числові квадрати для простого множника 210 та покажіть окремі кроки.
Примітка: Оскільки немає квадрата числа для 210, напишіть 210 на порожньому квадраті, щоб почати.
Рішення 1:\(210 = 21 \cdots 10 = 3 \cdots 7 \cdots 2 \cdots 5\)
Рішення 2:\(210 = 3 \cdots 70 = 2 \cdots 105 = 2 \cdots 3 \cdots 35 = 2 \cdots 3 \cdots 5 \cdots 7\)
Рішення 3:\(210 = 30 \cdots 7 = 5 \cdots 6 \cdots 7 = 5 \cdots 2 \cdots 3 \cdots 7\)
Є багато інших способів можна піти про факторинг 210, але врешті-решт, є 4 прості множники, які при множенні разом дорівнюють 210. Через комутативних і асоціативних властивостей множення,\(3 \cdots 7 \cdots 2 \cdots 5 = 2 \cdots 3 \cdots 5 \cdots 7 = 5 \cdots 2 \cdots 3 \cdots 7\). Зазвичай прості числа пишуться в порядку зростання (від найменшого фактора до найбільшого коефіцієнта. Пишемо, що просте факторизація 210 є\(2 \cdots 3 \cdots 5 \cdots 7\).
Це призводить до дуже важливої теореми. Ви можете розглядати прості числа як будівельні блоки для всіх цілих чисел, більших за 1. Кожне ціле число більше 1 є простим, або воно може бути виражене як добуток простих множників (називається простою факторизацією). Той факт, що будь-яке складене число можна записати як унікальний добуток простих чисел, настільки важливий, що його називають фундаментальною теоремою арифметики.
Фундаментальна теорема арифметики:
Кожне складене число має рівно одну унікальну просту факторизацію (за винятком порядку, в якому ви пишете множники).
Зауважте ще раз, що порядок написання факторів не має значення. Однак для узгодженості вони зазвичай пишуться в порядку зростання (від найменшого до найбільшого). Також експоненти можуть бути використані, якщо коефіцієнт повторюється при простому факторизації. Наприклад, просте факторизація 12 зазвичай пишеться як\(2 \cdots 2 \cdots 3\) або\(2^{2} \cdots 3\)
Використовуйте числові квадрати для простого множника кожне з наступних складових чисел у добуток простих чисел. Напишіть просту факторизацію так, щоб множники записувалися у порядку зростання (від найменшого до найбільшого). Жодне з цих чисел не є простим. Покажіть кожен з окремих кроків по одному, а не тільки кінцевий продукт.
| а. 45 = _____ |
| б. 65 = _____ |
| с. 200 = _____ |
| д. 91 = _____ |
| е. 76 = _____ |
| ф. 350 = _____ |
| г. 189 = _____ |
| ч. 74 = _____ |
| i. 512 = _____ |
| j. 147 = _____ |
Існують інші методи, які зазвичай використовуються для пошуку простого факторизації. Один використовує ФАКТОР ДЕРЕВО, який схожий на те, що ви зробили з простими і складовими квадратами числа. Різниця полягає в тому, що це робиться на папері, на відміну від використання маніпуляцій. Число, яке ви намагаєтеся зарахувати, називається коренем, і знаходиться вгорі. Отже, це насправді перевернуте дерево. Якщо число не є простим, ви малюєте дві гілки вниз від цього числа і вкажіть його як добуток будь-яких двох факторів. На кінці кожної гілки знаходиться менший фактор, який називається листом. Якщо листок простий, обведіть його, це один із факторів простої множини числа. В іншому випадку знову відгалужуються. Коли всі листя обведені простими числами, все готово. Першочерговим факторизацією кореня є продукт листя. Нижче наведено один із способів ми врахували 12, на попередній сторінці, використовуючи квадрати.

Ось окремі кроки, які показують, як можна використовувати дерево факторів для фактора 12, подібно до того, як це було враховано за допомогою квадратів, через шлях 1. Зверніть увагу на схожість.
|
Крок 1: Фактор 12 як 3d4  |
Крок 2: Коло 3, оскільки воно є простим  |
Крок 3 Обведіть 2s, оскільки вони прості  |
Крок 4: Обведіть 2s, оскільки вони прості 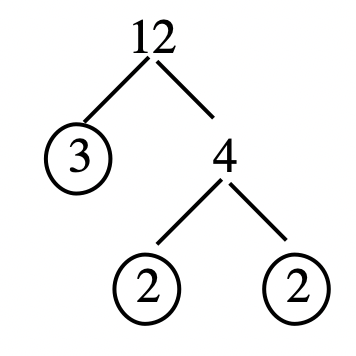 |
Крок 5: Просте факторизація 12 - добуток обведеного листя 3 d2 d2. |
Нижче наведено інший спосіб ми врахували 12 за допомогою квадратів.

Ось окремі кроки, які показують, як можна використовувати дерево факторів для фактора 12, подібно до того, як це було враховано за допомогою квадратів, через шлях 2. Знову зверніть увагу на схожість.
|
Крок 1: Фактор 12 як\(6 \times 2\)  |
Крок 2: Коло 2, оскільки воно є простим  |
Крок 3: Фактор 6 як\(2 \times 3\)  |
Крок 4: Коло 3 і 2, так як вони обидва прості.  |
Крок 5: Першочергове факторизація 12 - добуток обведеного листя.\(3 \cdots 2 \cdots 2\) |
Якщо ви не впевнені, чи є число простим або складеним, і не знаєте, як почати факторинг, скористайтеся тестами подільності. Подивіться, чи можна розділити на 2, 3, 5, 7, 11 тощо Переконайтеся, що немає факторів, перш ніж обвести його і вирішити, що це просте. Ви збираєтеся повторити вправу 4 ще раз, але цього разу використовуйте дерево факторів.
Скористайтеся деревом факторів, щоб перерахувати кожне з наступних складових чисел у добуток простих чисел. Напишіть просту факторизацію так, щоб множники записувалися у порядку зростання (від найменшого до найбільшого). Жодне з цих чисел не є простим. Покажіть окремі кроки. Показувати дерево факторів під кожною задачею.
| а. 45 = _____ | с. 200 = _____ |
| б. 65 = _____ | д. 91 = _____ |
| е. 76 = _____ | ч. 74 = _____ |
| ф. 350 = _____ | i. 512 = _____ |
| г. 189 = _____ | j. 147 = _____ |
Проблема з спробою знайти просту факторизацію полягає в тому, що іноді не очевидно, чи число, яке ви намагаєтеся фактор, є простим чи ні. Наприклад, не відразу видно, чи є 517 простим чи складовим. Ось тут і знадобляться тести на подільність. Насправді, якщо ви хочете знайти просту факторизацію 517, вам потрібно лише перевірити, чи має 517 прості числа як множники. Вам потрібно буде спробувати один прайм за раз. Перш ніж продовжувати, давайте перерахуємо перші кілька простих чисел, починаючи з 2. Примітка: 2 - єдине парне просте число. Щоб скласти список, почніть з 2, 3, 5 і перевірте, чи є наступне непарне число простим чи ні. Він не є простим, якщо одне з простих чисел, перерахованих раніше, є коефіцієнтом.
Перерахуйте всі прості числа менше 100. Вам потрібно використовувати лише тести подільності для 2, 3, 5 та 7, щоб перевірити, чи є будь-яке непарне число менше 100 простим. Іншими словами, будь-яке складене число менше 100 має 2, 3, 5 або 7 як множник. Ми обговоримо, чому після цієї вправи.
Розглянемо можливі способи фактора 54 як добутку 2-х факторів:
\(1 \cdots 54\),\(2 \cdots 27\),\(3 \cdots 18\),\(6 \cdots 9\),\(9 \cdots 6\),\(18 \cdots 3\),\(27 \cdots 2\),\(54 \cdots 1\)
Зауважте, що якщо ви починаєте з найменшого коефіцієнта (1) як лівого фактора, ви почнете повторювати список на півдорозі. Ця позначка «на півдорозі» відбувається після того, як ви потрапите до квадратного кореня числа, яке ви факторинг. Квадратний корінь з 54 знаходиться між 7 і 8. Так що, якщо ви перерахуєте коефіцієнт більше 7, це було б показано раніше в списку як коефіцієнт менше 7. Так що це означає, що якщо я намагаюся знайти просту факторизацію 54, мені потрібно тільки перевірити прості числа до і в тому числі не більше 7.
Так чому ж будь-яке складене число менше 100 має 2, 3, 5 або 7 як фактор? Наступне просте число після 7 - 11. Оскільки\(11^{2}\), або 121, більше 100, якщо було просте число більше або дорівнює 11, яке було коефіцієнтом числа менше 100, то інший коефіцієнт повинен бути менше 11. Подумайте про це. Якби обидва фактори були більшими за 11, продукт був би більше 121! Ця реалізація значно полегшує пошук простого факторизації числа. Ось як це працює.
Оскільки\(3^{2} = 9\) будь-яке складене число < 9 має 2 як множник.
Оскільки\(5^{2} = 25\) будь-яке складене число < 25 має 2 або 3 як множник.
Оскільки\(7^{2} = 49\) будь-яке складене число < 49 має 2, 3 або 5 як множник.
Оскільки\(11^{2} = 121\) будь-яке складене число < 121 має 2, 3, 5 або 7 як множник.
Оскільки\(13^{2} = 169\) будь-яке складене число <169 має 2, 3, 5, 7 або 11 як множник.
Оскільки\(17^{2} = 289\) будь-яке складене число < 289 має 2, 3, 5, 7, 11 або 13 як множник.
Оскільки\(19^{2} = 361\) будь-яке складене число < 361 має 2, 3, 5, 7, 11, 13 або 17 як множник.
Оскільки\(23^{2} = 529\) будь-яке складене число < 529 має 2, 3, 5, 7, 11, 13, 17 або 19 як множник.
Тепер ми перевіримо, що деякі з наведених вище тверджень вірні.
Оскільки\(3^{2} = 9\) будь-яке складене число < 9 має 2 як множник.
Це можна перевірити, перерахувавши складові числа менше 9 і показавши, що 2 є множником кожного з цих чисел: єдиними складовими числами менше 9 є 4, 6 і 8. Переконайтеся, що 2 є коефіцієнтом кожного з цих чисел:\(4 = 2 \cdots 2, 6 = 2 \cdots 3, 8 = 2 \cdots 4\)
Оскільки\(5^{2} = 25\) будь-яке складене число < 25 має 2 або 3 як множник.
У попередньому прикладі підтверджено, що складові числа менше 9 мають 2 або 3 як множник (оскільки ми показали, що всі вони мають 2 як множник). Таким чином, нам потрібно лише перерахувати та перевірити, що складені числа менше 25 мають 2 або 3 як множник. Єдиними складовими числами між 9 і 25 є 10, 12, 14, 15, 16, 18, 20, 21, 22 і 24. Подумки переконайтеся, що 2 або 3 є коефіцієнтом кожного з цих чисел. Примітка: кожне число повинно мати лише 2 АБО 3 як фактор, хоча воно може мати обидва. Наприклад, 2 - це коефіцієнт 10, 3 - коефіцієнт 15, і 2 і 3 - фактори 18. Вам потрібно лише переконатися, що принаймні один із цих факторів є фактором кожного складеного числа.
Оскільки\(7^{2} = 49\) будь-яке складене число < 49 має 2, 3 або 5 як множник. Перерахуйте складені числа між 25 і 49 і подумки переконайтеся, що 2, 3 або 5 є коефіцієнтом кожного з цих чисел.
Оскільки\(11^{2} = 121\) будь-яке складене число < 121 має 2, 3, 5 або 7 як множник. Перерахуйте складені числа між 49 і 121 і подумки переконайтеся, що 2, 3, 5 або 7 є множником кожного з цих чисел.
Це стає втомлюючим, намагаючись перевірити для більших чисел, але шаблон триває. Іншими словами, якщо ви перерахували всі складені числа менше 361, тобто\(19^{2}\), то ви могли б насправді перевірити, що кожен з них має 2, 3, 5, 7, 11 або 13 як коефіцієнт.
Отже, щоб знайти, якщо 517 є простим або складовим, оскільки 517 менше\(23^{2}\), мені потрібно лише перевірити, чи є будь-який з наступних факторів: 2, 3, 5, 7, 11, 13, 17 або 19. Замість того, щоб перевіряти кожне число до 517, потрібно перевірити лише ці вісім. Ви можете використовувати тести на подільність для перших п'яти простих чисел, потім використовувати калькулятор для останніх трьох. Якщо ви знайдете фактор на ранньому етапі, немає необхідності продовжувати йти.
Знайдіть просте факторизацію 517. Роблять це за допомогою тестів на подільність до 11, якщо це необхідно. Якщо ви все ще не знайдете коефіцієнт 517, скористайтеся калькулятором, щоб перевірити, чи є 13, 17 або 19 фактором. Напишіть тут просту факторизацію:
Оскільки я написав квадрати перших кількох простих чисел на попередній сторінці, я знав, що мені не потрібно перевіряти будь-які прості числа вище 19. Один із способів з'ясувати найбільше просте число, яке вам, можливо, доведеться перевірити, - це взяти квадратний корінь числа, яке ви намагаєтеся отримати простий множник.
На калькуляторі знайдіть квадратний корінь 517 округлений до найближчої десятої:
Ви повинні були отримати 22,7. Це говорить нам, що 517 не є ідеальним квадратом. Далі ми знаємо, що якщо 517 є складовим, він повинен мати простий коефіцієнт менше 22,7. Отже, нам потрібно визначити найбільше ціле число, яке є простим, яке менше 22,7. Почніть з 22 не простих; потім 21 не простий; потім 20 не простий; потім 19 простий! Тому нам максимум потрібно перевірити прості числа до 17:2, 3, 5, 7, 11, 13, 17 і 19. Коли ви насправді prime factored 517, ви помітили, що 11 був фактором? Ви використовували тест на подільність для 11?
Отже,\(517 = 11 \cdots 47\). Потім, ви дивитеся на інший фактор, 47, і зауважте, що він простий, так що ви закінчили! До речі, 5 - це найвищий прем'єр, який вам доведеться перевірити, чи 47 є основним!
Те, що ми щойно описали, - це теорема під назвою тест на основний фактор. Це формальний спосіб констатації цієї теореми.
Тест на прості множники числа n: Для перевірки простих множників числа n потрібно шукати лише прості множники p з n, де\(p^{2} \leq n\) (або\(p \leq \sqrt{n}\))
Для кожного числа визначте найвищий простий, який може знадобитися перевірити, щоб знайти просту факторизацію числа. Потім знайдіть просту факторизацію. Якщо він простий, просто напишіть саме число, оскільки це просте факторизація.
|
а. 149 найвищий прайм для перевірки: _____ Основна факторизація для 149: |
|
б. 273 найвищий прайм для перевірки: _____ Основна факторизація для 149: |
|
c. 381 найвищий прайм для перевірки: _____ Основна факторизація для 149: |
|
д. 437 найвищий прайм для перевірки: _____ Основна факторизація для 149: |
|
д. 509 найвищий прайм для перевірки: _____ Основна факторизація для 149: |
|
ф. 613 найвищий прайм для перевірки: _____ Основна факторизація для 149: |
|
г. 787 найвищий прайм для перевірки: _____ Основна факторизація для 149: |
Тепер давайте розглянемо діапазон чисел і розберемося, як визначити, які з них є простими. Наприклад, давайте визначимо, які числа між 350 і 370 є простими. Перш за все, прості лише непарні числа в цьому діапазоні. Отже, почнемо з перерахування непарних чисел в якості можливостей: 351, 353, 355, 357, 359, 361, 363, 365, 367 і 369. Далі, примітки 355 та 365 не можуть бути простими, оскільки вони діляться на 5. Тепер ви можете використовувати тест на подільність для 3, щоб перекреслити 351, 357, 363 та 369 примітки, які ви можете перетнути кратні 3, перетинаючи кожне третє непарне число, якщо ви починаєте з кратного 3. Тепер наш список зводиться до цих можливостей: 353, 359, 361, 367 та 369. Найвищий простий, який ви повинні перевірити, - це просте число, яке менше квадратного кореня 369, що дорівнює 19. Отже, просто перевірте решту простих чисел (не більше 7, 11, 13, 17 і 19) на кожному з цих чисел, щоб визначити, які, якщо такі є, прості. 353 є простим; 359 є простим; 361 - 19, 367 є простим. Отже, 353, 359 і 367 - це числа між 350 і 370, які є простими. Крім того, ви повинні мати можливість записати просту факторизацію для всіх чисел від 350 до 370, які є складовими.
Знайдіть просту факторизацію для всіх чисел від 280 до 295. Якщо число просте, просто напишіть саме число.
| а. 280 = ___________________ | i. 288 = ___________________ |
| б. 281 = ___________________ | j. 289 = ___________________ |
| c. 282 = ___________________ | к. 290 = ___________________ |
| д. 283 = ___________________ | л. 291 = ___________________ |
| е. 284 = _______________ | м. 292 = ___________________ |
| ф. 285 = _______________ | п. 293 = ___________________ |
| г. 286 = ___________________ | о. 294 = _______________ |
| ч. 287 = ___________________ | р. 295 = ___________________ |
Двомісні прості числа - це два послідовних непарних числа, які є простими. Наприклад, 5 і 7 - це подвійні прості числа, 11 і 13 - подвійні прості числа, 17 і 19 - подвійні прості числа. Немає шаблону, щоб визначити, як часто з'являються подвійні прості числа. Одне невирішене питання в математиці полягає в тому, чи існує скінченна кількість або нескінченно багато множин подвійних простих чисел. Ніхто не знає.
З вашої роботи у вправі 11 перерахуйте будь-які набори подвійних простих чисел: _____
Чи можна мати три непарні числа поспіль, які є простими? Чому чи чому ні?
Одне використання простого факторингу набору чисел полягає в тому, що ви можете знайти найбільший загальний коефіцієнт (GCF) та найменш спільний кратний (LCM) набору чисел. Багато людей мають проблеми з розрізненням між найбільшим загальним фактором і найменш загальним кратним (LCM), тому що вони не думають про те, що насправді означають слова. Найбільший загальний фактор числа, очевидно, фактор, але прикметник загальний описує, що ви хочете фактор, який є загальним для всіх чисел, і прикметник найбільший описує, що ви хочете найбільший із загальних факторів чисел.
Ми будемо досліджувати способи знаходження найбільшого спільного множника двох чисел, a і b, позначення, щоб висловити це, є GCF (a, b). Не має значення, який номер ви перерахуєте першим у дужках - це не впорядкована пара. Найбільшим загальним фактором набору чисел є найбільше число, яке є коефіцієнтом кожного числа.
Ми будемо досліджувати різні способи знаходження найбільшого спільного фактора двох чисел.
По-перше, ми будемо досліджувати один із способів знайти найбільший загальний фактор 42 і 72. Позначення, щоб висловити це, є GCF (42, 70). Пам'ятайте: неважливо, який номер ви перерахуєте першим у дужках, це не впорядкована пара. GCF (42, 70) означає те ж саме, що і GCF (70, 42). Найбільший загальний фактор 42 і 70 - це найбільше число, яке є коефіцієнтом як 42, так і 70.
Один із способів зробити це - перерахувати кожен фактор кожного числа, а потім вибрати найбільший, який є фактором кожного.
| а. перерахуйте всі фактори 42 в порядку зростання: ____ |
| б. перерахуйте всі фактори 70 в порядку зростання: ____ |
| c Перерахуйте всі фактори, які є загальними як для 42, так і для 70: ____ |
| d Перерахуйте найбільший загальний коефіцієнт 42 і 70: ____ |
| е Заповніть бланк: GCF (42, 70) = ____ |
Перерахування всіх факторів даного числа іноді буває складним завданням. Наприклад, легко пропустити фактор. Одним із засобів є простий множник числа першим. Щоб перелічити всі фактори 42, можна спочатку простий множник 42, як це:\(2 \cdots 3 \cdots 7\). Щоб число було коефіцієнтом 42, воно повинно складатися з перерахованих простих факторів. Звичайно, 1 - це завжди фактор. Далі ви перевіряєте 2, а потім 3, які є обома факторами. 4 не є фактором, тому що якби це було, було\(2 \cdots 2\) б у простому факторизації! Зрозуміло, що 5 - це не фактор. 6 - це фактор, оскільки\(2 \cdots 3\) знаходиться в простій факторизації. Продовжуючи далі, 7 є фактором, але 8 не\(2 \cdots 2 \cdots 2\) тому, що не в простому факторизації 42. Ні 9\((3 \cdots 3), 10 (2 \cdots 5), 11, 12 (2 \cdots 2 \cdots 3)\), ні 13. Але 14 - це коефіцієнт 42, оскільки\(2 \cdots 7\) знаходиться в першій факторизації. Ви можете використовувати цю стратегію, перевіряючи кожне число до 42, але це ще багато цифр, щоб перевірити. Врешті-решт, ви отримаєте цей список: 1, 2, 3, 6, 7, 14, 21, 42.
Ось спосіб скоротити процес трохи більше. Починаючи з найменшого коефіцієнта 1, негайно перерахуйте інший коефіцієнт, який вам доведеться помножити на цей коефіцієнт, щоб отримати 42. Отже, починаємо з 1, 42. Ми перевіряємо наступне число, 2, і відзначаємо, що це фактор. Щоб отримати інший фактор, який поєднується з 2, або розділіть 2 на 42, або просто подивіться на просте факторизацію 42, при цьому 2 відсутні. \(3 \cdots 7\)Залишилося, що є іншим фактором. Таким чином, список тепер 1, 42, 2, 21. Продовжуючи, відзначимо 3 - це фактор. Щоб отримати інший фактор, або розділіть 42 на 3, або зробіть це простим способом, який полягає в тому, щоб побачити, які фактори залишилися в простому факторизації 42 з відсутніми 3. Так як є 2 і 7, то число, яке пара вгору з 3 дорівнює 14.
Список зараз 1, 42, 2, 21, 3, 14. Далі ми зауважимо 4 і 5 не множники. 6 - коефіцієнт, оскільки 2 і 3 (\(2 \cdots 3\)) знаходиться в простій факторизації. 7 - це число, яке поєднується з 6. Отже, список зараз: 1, 42, 2, 21, 3, 14, 6, 7. Якби ви продовжили, наступним номером для перевірки буде 7. Починаючи з\(7^{2}\) > 42, ви можете зупинитися. Усі фактори, які перевищують 7, вже будуть у списку, оскільки був би менший фактор, з яким він вже поєднав. Тепер поставте список факторів 42 у порядку зростання: 1, 2, 3, 6, 7, 14, 21, 42.
Цією ж процедурою можна перерахувати всі фактори 70. Спочатку напишіть просту факторизацію 70:\(2 \cdots 5 \cdots 7\). Ви б починали з 1 і 70:1, 70. Далі, зрозуміло, що 2 - це фактор, який поєднується з 35. Список зараз: 1, 70, 2, 35. Далі відкиньте 3 і 4 як фактори, а примітка 5 - фактор. Залишилися коефіцієнти 2 і 7, які помножені разом на 14. Отже, список 1, 70, 2, 35, 5, 14. Продовжуючи далі, примітка 6 не є фактором, а 7 є. 7 пар вгору з 10. Список зараз: 1, 70, 2, 35, 5, 14, 7, 10. Продовжуючи далі, зверніть увагу, що 8 не є фактором. Наступним номером для перевірки буде 9. Але\(9^{2}\) > 70, тому всі фактори вище вже є в списку. Записуючи список в порядку зростання, отримуємо: 1, 2, 5, 7, 10, 14, 35, 70.
Зверніть увагу, що в обох цих прикладах 42 та 70 мали рівно 3 простих числа у простому факторизації. Розглянемо просту факторизацію 220:\(2 \cdots 2 \cdots 5 \cdots 11\). Зауважте, що при переліку факторів може бути один, два або три інші фактори, які потрібно помножити разом\(2 \cdots 5 \cdots 11\), щоб отримати пару. 2 - коефіцієнт; його пара - або 110. 4\((2 \cdots 2\)) - коефіцієнт; його пара - 5,\(\cdots\) 11 або 55. 5 - коефіцієнт; його пара -\(2 \cdots 2 \cdots 11\) або 44. 10 (\(2 \cdots 5\)) - коефіцієнт; його пара є\(2 \cdot 11\), або 22. 11 є фактором; його пара\(2 \cdots 2 \cdots 5\), або 20. Оскільки я перевіряю числа більше 11, я зупиняюся на 15 з 152 > 220. Отже, список такий: 1, 220, 2, 110, 4, 55, 5, 44, 10, 22, 11, 20. Записуючи ці в порядку зростання, отримуємо: 1, 2, 4, 5, 10, 11, 20, 22, 44, 55, 110, 220.
До речі, це набагато більше часу для мене, щоб пояснити (і для вас прочитати), як перерахувати всі фактори шляхом простого факторингу. Але зробити це набагато простіше! Тепер виконайте наступні вправи. Якщо ви хочете, використовуйте просту факторизацію, щоб зробити частини a та b.
Мета цієї проблеми - знайти найбільший спільний фактор 92 і 115.
| a. перерахуйте всі фактори 92 в порядку зростання: |
| б. перерахуйте всі фактори 115 в порядку зростання: |
| c Перерахуйте всі фактори, які є загальними і для 92, і 115: |
| d Перерахуйте найбільший загальний коефіцієнт 92 і 115: |
| е. заповнити бланк: GCF (92, 115) = |
Мета цієї проблеми - знайти найбільший спільний фактор 48, 54 і 63.
| a. перерахуйте всі фактори 48 в порядку зростання: |
| б. перерахуйте всі фактори 54 в порядку зростання: |
| c Перерахуйте всі фактори 63 в порядку зростання: |
| d Перерахуйте всі фактори, які є загальними для 48, 54, а також 63: |
| е Перерахуйте найбільший загальний коефіцієнт 48, 54 і 63: |
| f Заповніть бланк: GCF (48, 54 і 63) = |
Як ви могли зрозуміти, перерахування факторів все ще може бути дуже трудомістким способом знайти найбільший загальний фактор, особливо якщо цифри дуже великі або мають багато факторів.
Прийшов час, щоб отримати кольорові квадрати з простим числом та білі складові квадрати з числом знову. Ми будемо використовувати їх для простого множника наборів чисел, які потім можуть бути використані, щоб знайти найбільший загальний коефіцієнт набору чисел. Цей спосіб, як правило, швидше, ніж той, який ми тільки що використовували.
Мета цього наступного прикладу полягає в тому, щоб знайти найбільший спільний коефіцієнт 42 та 72 за допомогою простої факторизації з простими та складовими квадратами чисел.
Крок 1: Використовуйте квадрати, щоб простий коефіцієнт 42 і 72.
\(42 = 2 \cdots 3 \cdots 7\)і\(72 = 2 \cdots 2 \cdots 2 \cdots 3 \cdots 3\)
Крок 2: Намалюйте лінію і поставте над нею прості множники 42. Поруч з цим проведіть лінію і поставте над нею прості множники 72.

Крок 3: Подивіться на просту факторизацію чисел. Перемістіть кожен фактор, який вони мають спільного, під лінією. Вони повинні мати однакові точні фактори під лінією, і вони не повинні мати загальних факторів, залишених над лінією.
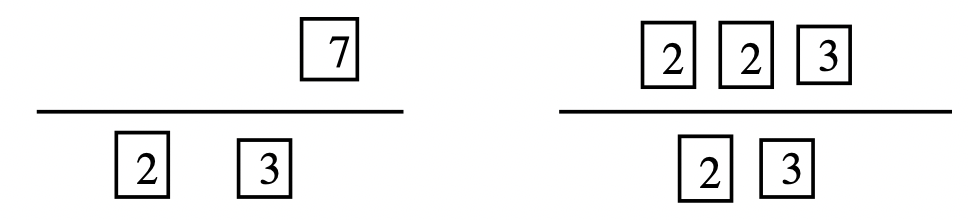
Крок 4: Добуток факторів під рядком є найбільшим загальним фактором чисел. При цьому 2,\(\cdots\) 3, або 6, є найбільшим загальним фактором 42 і 72.
Крок 5: Використовуйте правильні позначення, щоб написати відповідь: GCF (42, 70) = 6.
Наступний приклад використовував ті самі кроки, щоб знайти найбільший спільний коефіцієнт 16, 24 і 36.
Крок 1: Використовуйте квадрати, щоб простий коефіцієнт 16, 24 і 36.
\(16 = 2 \cdots 2 \cdots 2 \cdots 2, 24 = 2 \cdots 2 \cdots 2 \cdots 3\)і\(36 = 2 \cdots 2 \cdots 3 \cdots 3\)
Крок 2: Намалюйте лінію для кожного числа і поставте прості множники кожного числа над ним.
 |
 |
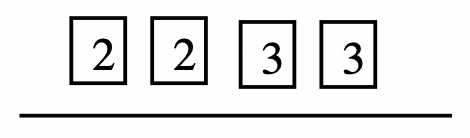 |
Крок 3: Подивіться на просту факторизацію чисел. Перемістіть кожен фактор, який мають спільні всі три числа. Над рядком, який мають спільні всі три числа, не повинно бути ніяких факторів.
 |
 |
 |
Крок 4: Добуток факторів під рядком є найбільшим загальним фактором чисел. При цьому,\(2 \cdots 2\) або 4, є найбільшим поширеним фактором 16, 24 і 36.
Крок 5: Використовуйте правильні позначення, щоб написати відповідь: GCF (16, 24, 36) = 4.
Скористайтеся кроками, показаними в попередніх двох прикладах, щоб знайти найбільший спільний фактор кожної проблеми. Покажіть картину того, як виглядає проблема на кроці 3, де просте факторизація найбільшого спільного коефіцієнта показана під рядком кожного числа, яке ви вперше просте факторизували.
|
а. gcf (42, 70) = _____ (Ця відповідь повинна погодитися з вправою 14е.) Показати роботу нижче: |
|
б. GCF (92, 115) = _____ (Ця відповідь повинна погодитися з вправою 15е.) Показати роботу нижче: |
|
c. GCF (48, 54, 63) = _____ (Ця відповідь повинна погодитися з вправою 16ф.) Показати роботу нижче: |
|
д. ГКФ (306, 340) = _____ Показати роботу нижче: |
|
е. ЗКФ (125, 275, 400) = _____ Показати роботу нижче: |
|
ф. ГКФ (126, 168, 210) = _____ Показати роботу нижче: |
Скажімо, хтось простий фактор три великі числа, X, Y і Z, як це:
| \(X = 2^{5} \cdots 3^{4} \cdots 7^{2} \cdots 11^{8} \cdots 13^{3}\) | \(Y = 2^{4} \cdots 3^{5} \cdots 5^{3} \cdots 7^{7} \cdots 13^{2}\) | \(Z = 2^{6} \cdots 3 \cdots 5^{5} \cdots 11^{3} \cdots 13^{4}\) |
а. стан простої факторизації (експоненціальне позначення є нормальним) найбільшого спільного коефіцієнта X, Y та Z. GCF (X, Y, Z) =
б Поясніть, як ви зробили частину a.
Один із способів виконання попередньої вправи полягає в тому, щоб почати з перерахування загальних простих факторів (без показників) X, Y і Z. вони 2, 3 і 13. Отже, для початку напишіть 2\(\cdots\) 3\(\cdots\) 13. Далі визначте, скільки кожного простого коефіцієнта є загальним для X, Y та Z. оскільки X має 5 факторів 2, Y має 4 множники 2, а Z має 6 факторів 2, вони мають лише 4 множники 2. Аналогічно, вони мають лише один коефіцієнт 3 спільного та 2 фактори з 13 спільних. Помістіть ці показники на фактори, і ви отримаєте GCF з трьох чисел: GCF (X, Y, Z) =\(2^{4} \cdots 3 \cdots 13^{2}\)
Чи помітили ви, що якщо ви перерахуєте загальні фактори без показників, ви ставите найменший показник, який вони мають спільну для кожного простого?
Напишіть просту факторизацію найбільшого спільного множника множини чисел. Для тих, які враховуються літерами, припустимо, що кожна буква являє собою інше просте число.
|
а. якщо\(X = 2^{4} \cdots 3^{2} \cdots 7^{6} \cdots 11^{3} \cdots 13^{2}\) і\(Y = 2^{5} \cdots 3^{6} \cdots 5^{4} \cdots 7^{6} \cdots 13^{3}\) ГКФ (Х, У) = _______________________ |
|
б. якщо\(X = 3^{4} \cdots 5^{2} \cdots 7^{6}\) і\(Y = 2^{5} \cdots 3^{6} \cdots 5^{6} \cdots 7^{3}\) і\(Z = 2^{4} \cdots 3^{5} \cdots 5^{4}\) ГКФ (Х, У, З) = _____________________ |
|
c. якщо\(X = a^{4} \cdots b^{2} \cdots c^{6} \cdots d^{3} \cdots e^{2}\) і\(Y = a^{5} \cdots c^{3} \cdots d^{4} \cdots e^{6} \cdots f^{3}\) ГКФ (Х, У) = _______________________ |
|
d. якщо\(X = a^{4} \cdots b \cdots c^{4} \cdots d^{3}\) і\(Y = a^{5} \cdots b^{3} \cdots d^{4} \cdots e^{6}\) і\(Z = a^{2} \cdots c^{3} \cdots d^{7} \cdots f^{3}\) ГКФ (Х, У, З) = _____________________ |
Якщо два числа не мають спільних множників, їх називають відносно простими. Іншими словами, якщо GCF (a, b) = 1, то a і b є відносно простими. Числа, a і b, можуть бути простими, обидва бути складовими, або одне може бути простим, а іншим складовим.
Наведіть приклад двох складових чисел, які є відносно простими:
Напишіть просте і складене число, які є відносно простими:
Припустимо, GCF (28, х) = 1
а. перерахуйте будь-які прості числа, які не є множниками x: ____________________________
б. наведіть три приклади (числа) того, що х міг дорівнювати: ___________________
Якщо x і y є різними простими числами, GCF (x, y) = _____
Якщо m - ціле число, знайдіть наступне:
| а. ГКФ (2м, 3м) = _______ | б. ГКФ (4м, 10м) = ________ |
| c. ЗКФ (м, м) = _______ | д. ГКФ (м, 1) = _______ |
| е. ЗКФ (м, 0) = _______ |
Спроба знайти найбільший спільний коефіцієнт двох великих чисел шляхом простої факторизації іноді досить трудомістка. Є ще два алгоритми, які ви можете використовувати, які ми будемо використовувати. Один називається Старий китайський метод, а інший - Евклідовим алгоритмом. Обидва ці методи використовують факт, який ми можемо довести, використовуючи те, що ми знаємо про подільність. Для початку розглянемо кілька прикладів.
Обчисліть кожне з таких дій:
| а. перерахуйте загальні фактори 42 і 72: _______ |
| б. перерахуйте загальні фактори 42 і 30 (що дорівнює 72 — 42): _______ |
| c Перерахуйте загальні фактори 30 і 12 (що становить 42 — 30): _______ |
| d Перерахуйте загальні фактори 12 і 18 (що становить 30 — 12): _______ |
| е Перерахуйте загальні фактори 12 і 6 (що становить 18 — 12): _______ |
| f Перерахуйте загальні фактори 6 і 6 (що становить 12 — 6): _______ |
| м Перерахуйте загальні фактори 6 і 0 (що становить 6 — 6): _______ |
Вправа 26
З вашої роботи у вправі 25 обчислити наступне:
| а. ГКФ (42, 72) = ____ | б. ГКФ (42, 30) = ____ |
| c. ЗКФ (30, 12) = ____ | д. ЗКФ (12, 18) = ____ |
| е. ЗКФ (12, 6) = ____ | f. ЗКФ (6, 6) = ____ |
| г ЗКФ (6, 0) = ____ |
Попередні дві вправи ілюструють, що найбільший спільний множник двох чисел дорівнює найбільшому спільному фактору меншого числа, і різниці вихідних двох чисел; тобто якщо x\(\boldsymbol{\geq}\) y, то GCF (x, y) = GCF (y, x — y).
Доведіть наступну теорему: Нехай a\(\boldsymbol{\geq}\) b Якщо c|a і c|b, то c| (a — b).
Розв'язок: Якщо c|a, то cn=a для деякого цілого числа, n Якщо c|b, то cm=b для деякого цілого числа, m. Використовуючи ці заміни для a та b, отримаємо, що c| (a — b) є істинним, якщо c| (cn — cm), що вірно, якщо c є множником cn — cm. Коефіцієнт: cn — см = c (n — м). Це чітко показує, що c дійсно є коефіцієнтом cn — см. Тому якщо c|a і c|b, то c| (a — b).
Ця теорема може бути використана для того, щоб показати, що якщо a\(\boldsymbol{\geq}\) b, то GCF (a, b) = GCF (b, a — b). Вищевказана теорема стверджує, що якщо c - множник двох чисел, то це також коефіцієнт їх різниці. Отже, якщо c є загальним фактором a та b, де a\(\geq\), то c також є загальним фактором b та a — b, оскільки кожен спільний множник a та b також є загальним фактором ba та a — b, пари (a, b) та (b, a — b) мають однакові загальні фактори. Отже, GCF (a, b) і GCF (b, a — b) також повинні бути однаковими.
Старокитайський метод використовує той факт, що GCF (a, b) = GCF (b, a — b).
Зверніть увагу на ще три властивості:
GCF (x, x) = x: GCF (x, x) стверджує, що найбільшим спільним коефіцієнтом тих же двох чисел є сам собою. Це повинно бути зрозуміло, оскільки x є найбільшим коефіцієнтом кожного числа, тому кожен має x як найбільший загальний фактор.
GCF (x, 0) = x: GCF (x, 0) = x, є істинним, оскільки кожне число дорівнює нулю. Так, так як х є найбільшим коефіцієнтом х, то х є найбільшим загальним коефіцієнтом х і 0.
GCF (x, 1) = 1: GCF (x, 1) = 1 є істинним, оскільки 1 є коефіцієнтом кожного числа, включаючи x, а 1 - єдиний коефіцієнт 1. Тому 1 повинен бути найбільшим загальним коефіцієнтом 1 і х.
Старокитайський метод знаходження найбільшого спільного множника двох чисел:
Запишіть GCF двох чисел в дужках (пам'ятайте, порядок чисел не має значення). Нехай це дорівнює GCF меншого з двох чисел, і різниця вихідних двох чисел. Якщо цифри в дужках однакові, це число є GCF; якщо одне нове число дорівнює 1, 1 - це GCF. В іншому випадку повторюйте процес до тих пір, поки два числа не будуть однаковими, або 1 - одне з чисел. Приклад наведено нижче. Праворуч - пояснення того, як я отримав два нових числа в дужках. Нові цифри підкреслені в поясненні. Вам не потрібно це виписувати.
| ГКФ (546, 390) | = ГКФ (390, 156) | (390 менше 546, 390 = 546 — 390) |
| = ГКФ (156, 234) | (156 менше 390, 234 = 390 - 156) | |
| = ГКФ (156, 78) | (156 менше 234, 78 = 234 - 156) | |
| = ГКФ (78, 78) | (78 менше 156, 78 = 156 - 78) | |
| = 78 | 78 - це GCF (78, 78); Відповідь - число! |
Тому ГКФ (546, 390) = 78.
Перевірка: По-перше, переконайтеся, що 78 є коефіцієнтом 546 і 390:\(546 = 78 \cdots 7\) і\(390 = 78 \cdots 5\). По-друге, перевірте, щоб переконатися, що інші фактори кожного (7 і 5) є відносно простими. Якщо так, то 78 - це не тільки коефіцієнт 546 і 390, але насправді є найбільшим загальним фактором кожного, оскільки вони не мають інших загальних факторів (оскільки 7 і 5 не мають загальних факторів).
Інший приклад наведено нижче. Праворуч - пояснення того, як я отримав два нових числа (підкреслені) в дужках. Вам не потрібно це виписувати.
| ГКФ (1200, 504) | = ГКФ (504, 696) | (504 менше 1200, 696 = 1200 - 504) |
| = ГКФ (504, 192) | (504 менше 696, 192 = 696 — 504) | |
| = ГКФ (192, 312) | (192 менше 504, 312 = 504 — 192) | |
| = ГКФ (192, 120) | (192 менше 312, 120 = 312 — 192) | |
| = ГКФ (120, 72) | (120 менше 192, 72 = 192 - 120) | |
| = ГКФ (72, 48) | (72 менше 120, 48 = 120 - 72) | |
| = ГКФ (48, 24) | (48 менше 72, 24 = 72 - 48) | |
| = ГКФ (24, 24) | (24 менше 48, 24 = 48 - 24) | |
| = 24 | 24 - це GCF (24, 24); Відповідь - число! |
Тому ГКФ (1200, 504) = 24.
Перевірка: По-перше, переконайтеся, що 24 є коефіцієнтом 1200 і 504:1200 =\(24 \cdots 50\) і\(502 = 24 \cdots 21\). По-друге, перевірте, чи інші фактори кожного (25 та 21) є відносно простими. Якщо так, то 24 - це не тільки коефіцієнт 1200 і 504, але насправді є найбільшим загальним фактором кожного, оскільки вони не мають інших загальних факторів (оскільки 25 і 21 не мають загальних факторів.)
Ось ще один приклад:
| ГКФ (667, 437) | = ГКФ (437, 230) | |
| = ГКФ (230, 207) | ||
| = ГКФ (207, 23) | ||
| = ГКФ (23, 184) | ||
| = ГКФ (23, 161) | ||
| = ГКФ (23, 138) | ||
| = ГКФ (23, 115) | ||
| = ГКФ (23, 92) | ||
| = ГКФ (23, 69) | ||
| = ГКФ (23, 46) | ||
| = ГКФ (23, 23) | ||
| = 23 | Пам'ятайте: Відповідь - це число! |
Тому ГКФ (667, 437) = 23.
Перевірка: По-перше, переконайтеся, що 23 - це коефіцієнт 667 та 437:\(667 = 23 \cdots 29\) і\(437 = 23 \cdots 19\). По-друге, перевірте, чи інші фактори кожного (29 та 19) є відносно простими. Якщо так, то 23 - це не лише коефіцієнт 667 та 437, але насправді є найбільшим загальним фактором кожного, оскільки вони не мають інших загальних факторів (оскільки 29 та 19 не мають загальних факторів.)
Коментар: Ви могли б отримати найбільший спільний фактор з попередніх трьох прикладів шляхом простого факторингу. Часто це тривалий процес для великих чисел, які виглядають так, ніби вони можуть бути простими, як в останньому прикладі. Тому старокитайці надає альтернативний спосіб отримання найбільшого загального фактора. Виконавши кілька застосувань цього методу, ми розглянемо інший альтернативний метод, який називається евклідовим алгоритмом, який пов'язаний, але зазвичай займає менше кроків, ніж старий китайський метод.
Використовуйте старий китайський метод, щоб обчислити найбільший загальний коефіцієнт заданих чисел. Використовуйте правильні позначення та показуйте кожен крок. Викладіть відповідь. Потім покажіть, як ви перевіряєте свою відповідь. Використовуйте попередній приклад як модель для вирішення цих проблем.
|
а.
|
||||||||||||||||||||||||||||||
|
б.
|
||||||||||||||||||||||||||||||
|
c.
|
Використання китайського методу може бути досить нудним. Погляньте на наступний приклад:
| ГКФ (1200, 504) | = ГКФ (504, 696) | (504 менше 1200, 696 = 1200 - 504) |
| = ГКФ (504, 192) | (504 менше 696, 192 = 696 — 504) | |
| = ГКФ (192, 312) | (192 менше 504, 312 = 504 — 192) | |
| = ГКФ (192, 120) | (192 менше 312, 120 = 312 — 192) | |
| = ГКФ (120, 72) | (120 менше 192, 72 = 192 - 120) | |
| = ГКФ (72, 48) | (72 менше 120, 48 = 120 - 72) | |
| = ГКФ (48, 24) | (48 менше 72, 24 = 72 - 48) | |
| = ГКФ (24, 24) | (24 менше 48, 24 = 48 - 24) | |
| = 24 | 24 - це GCF (24, 24); Відповідь - число! |
На початку цього прикладу, GCF (1200, 504), нам довелося віднімати 504 двічі, поки ми не отримали GCF (504, 192). Потім, зверніть увагу, як тільки ми написали GCF (504, 192), ми повинні були відняти 192 двічі, поки ми не отримали GCF (192, 120). В основному, ми робимо повторне віднімання, поки ми не отримаємо число менше, ніж той, який ми віднімаємо. Повторне віднімання - це фактично ділення. Зверніть увагу, що\(1200 \div 504 = 2\) залишок 192. На другому кроці ми бачимо GCF (504, 192), який має меншу кількість чисел у вихідних дужках (504), а залишок після ділення більшого числа (1200) на менше число (504). Зверніть увагу, що\(504 \div 192 = 2\) залишок 120. Подивіться на четвертий крок: ми бачимо GCF (192, 120), який має меншу з чисел в GCF (504, 192), а залишок після ділення більшого числа (504) на менше число (192). Алгоритм Евкліда використовує ділення замість повторного віднімання, щоб скоротити кроки.
Як використовувати Евклідовий алгоритм, щоб знайти найбільший спільний множник двох чисел:
Запишіть GCF двох чисел в дужках (пам'ятайте, порядок чисел не має значення). Менше з двох чисел буде одним із чисел у наступних дужках. Щоб отримати інше число, розділіть більшу кількість на меншу кількість, а залишок поставте в дужки. Якщо менша кількість є коефіцієнтом більшого числа, це означає, що воно буде ділитися рівномірно, тому залишку не буде. Це означає, що залишок дорівнює 0. Не забудьте поставити залишок у дужках, а не частку! Якщо одне з нових чисел у дужках дорівнює нулю, інше число є GCF; якщо одне нове число дорівнює 1, 1 - GCF. В іншому випадку повторюйте процес, поки одне з двох чисел не буде 0 або 1. Приклад наведено нижче. Це перший приклад, який ми зробили за допомогою старого китайського методу. Можливо, ви захочете озирнутися назад і порівняти. Праворуч - пояснення того, як я отримав два нових числа в дужках.
| ГКФ (546, 390) | = ГКФ (390, 156) | (390 менше 546,\(546 \div 390\) = 1 р 156) |
| = ГКФ (156, 78) | (156 менше 390,\(390 \div 156\) = 2 р 78) | |
| = ГКФ (78, 0) | (78 менше 156,\(156 \div 78\) = 2 r 0) | |
| = 78 | Поставте залишок (0), А НЕ 2, в дужки! | |
| 78 - це GCF (78, 78); Відповідь - число! |
Тому ГКФ (546, 390) = 78
Перевірка: По-перше, переконайтеся, що 78 є коефіцієнтом 546 і 390:\(546 = 78 \= \cdots 7\) і\(390 = 78 \cdots 5\). По-друге, перевірте, щоб переконатися, що інші фактори кожного (7 і 5) є відносно простими. Якщо так, то 78 - це не тільки коефіцієнт 546 і 390, але насправді є найбільшим загальним фактором кожного, оскільки вони не мають інших загальних факторів (тому що 7 і 5 не мають загальних факторів).
Нижче наведено ще один приклад — ми робили це раніше за допомогою старокитайського методу. Праворуч - пояснення того, як я отримав два нових числа в дужках. Вам не потрібно це виписувати.
| ГКФ (667, 437) | = ГКФ (437, 230) | (437 менше, ніж 667,\(667 \div 437 = 1\) р 230) |
| = ГКФ (230, 207) | (230 менше 437,\(437 \div 230 = 1\) р 207) | |
| = ГКФ (207, 23) | (207 менше 230,\(230 \div 207\) = 1 р 23) | |
| = ГКФ (23, 0) | (23 менше 207,\(207 \div 23\) = 9 r 0) | |
| = 23 | Поставте залишок (0), А НЕ 9, в дужки! | |
| Пам'ятайте: Відповідь - це число! |
Тому ГКФ (667, 437) = 23
Перевірка: По-перше, переконайтеся, що 23 є коефіцієнтом 667 і 437:667 =\(23 \cdots 29\) і\(437 = 23 \cdots 19\). По-друге, перевірте, чи інші фактори кожного (29 та 19) є відносно простими. Якщо так, то 23 - це не лише коефіцієнт 667 та 437, але насправді є найбільшим загальним фактором кожного, оскільки вони не мають інших загальних факторів (оскільки 29 та 19 не мають загальних факторів.)
Коментар: Ви могли б отримати найбільший спільний фактор з попередніх трьох прикладів шляхом простого факторингу, старокитайського методу або евклідового алгоритму.
УВАГА: НАЙПОШИРЕНІША ПОМИЛКА, ЯКУ ЛЮДИ ДОПУСКАЮТЬ ПРИ ВИКОРИСТАННІ ЕВКЛІДОВОГО АЛГОРИТМУ, ЗНАХОДИТЬСЯ НА ОСТАННЬОМУ КРОЦІ, КОЛИ МЕНШЕ ЧИСЛО ДІЛИТЬСЯ РІВНОМІРНО НА БІЛЬШУ КІЛЬКІСТЬ, А ЦЕ ОЗНАЧАЄ, ЩО ЗАЛИШОК ДОРІВНЮЄ НУЛЮ. НЕВАЖЛИВО, ЩО ЧАСТКА - ЦЕ РЕШТА, ЯКА МАЄ ЗНАЧЕННЯ - 0 ЙДЕ В ДУЖКАХ!!! Крім того, нуль не є коефіцієнтом будь-якого числа, крім нуля, тому GCF не може бути нулем. З іншого боку, кожне число - це коефіцієнт нуля. Отже, коли нуль - одне з чисел в дужках, інше число - це GCF. НЕ ЗАБУДЬТЕ ЗАВЖДИ ПЕРЕВІРЯТИ СВОЮ ВІДПОВІДЬ!!!
Перш ніж продовжувати, я збираюся нагадати вам про швидкий і простий спосіб дізнатися частку і залишок за допомогою простого калькулятора при виконанні цих завдань поділу, де вам потрібно знайти залишок. Якщо ви вже можете зробити це легко або ваш калькулятор з'ясовує це для вас, перейдіть до Вправи 29. Припустимо, ви хотіли розділити\(5263 \div 360\). Коли ви робите це на калькуляторі, він показує щось на зразок 14.619444. Це вказує на те, що в 5263 є 14 360, але решта не очевидна. Принаймні, ви знаєте, що 14 є часткою. Щоб знайти залишок на калькуляторі, введіть\(14 \times 360\) - 5263 і число, що відображається, є залишком, якщо ви ігноруєте негативний знак! В даному випадку залишок дорівнює 223. Пам'ятайте, що залишок повинен бути меншим, ніж ви спочатку розділили - менше 360 в цьому випадку. Подумайте, чому цей процес працює, і спробуйте його на наступних кількох проблемах.
Використовуйте калькулятор, щоб знайти частку та залишок для цих задач ділення.
| а.\(9876 \div 255\) = | б.\(1509 \div 164\) = |
| с.\(333 \div 46\) = | д.\(4657 \div 579\) = |
Використовуйте Евклідовий алгоритм для обчислення найбільшого спільного коефіцієнта заданих чисел. Використовуйте правильні позначення та показуйте кожен крок. Викладіть відповідь. Потім покажіть, як ви перевіряєте свою відповідь. Використовуйте попередній приклад як модель для вирішення цих проблем. Це ті самі вправи, які ви робили за допомогою старого китайського методу у вправі 27. Можливо, ви захочете порівняти два методи, коли ви закінчите. Звичайно, відповідь повинна бути однаковою.
|
а.
|
|||||||||||||||
|
б.
|
|||||||||||||||
|
c.
|
Знайдіть GCF (418, 88) за допомогою трьох обговорюваних методів:
| а) шляхом первинної факторизації; |
| б) за старокитайським методом; |
| в) за Евклідовим алгоритмом |
| г) Напишіть відповідь, і покажіть, як перевірити відповідь. |
| a. використовувати просте факторизацію | c Використовувати евклідовий алгоритм |
| б Використовуйте старий китайський метод | d. відповідь: GCF (418, 88) = _______ Перевірте свою відповідь |
Знайдіть GCF (527, 465) за допомогою трьох обговорюваних методів:
| а) шляхом первинної факторизації; |
| б) за старокитайським методом; |
| в) за Евклідовим алгоритмом |
| г) Напишіть відповідь, і покажіть, як перевірити відповідь. |
| a. використовувати просте факторизацію | c Використовувати евклідовий алгоритм |
| б Використовуйте старий китайський метод | d. відповідь: GCF (527, 465) = _______ Перевірте свою відповідь |
Знайдіть GCF (353, 213) за допомогою трьох обговорюваних методів:
| а) шляхом первинної факторизації; |
| б) за старокитайським методом; |
| в) за Евклідовим алгоритмом |
| г) Напишіть відповідь, і покажіть, як перевірити відповідь. |
| a. використовувати просте факторизацію | c Використовувати евклідовий алгоритм |
| б Використовуйте старий китайський метод | d. відповідь: GCF (353, 213) = _______ Перевірте свою відповідь |
Тепер, коли ми розглянули багато про прості числа та факторинг, ми збираємося переглянути тести подільності ще раз.
Зверніть увагу, що тест на подільність для 6 використовував два інших тести подільності, один для 2 і один для 3. Також зверніть увагу, що тест на подільність для 15 використовував два інших тести подільності, один для 5 і 3. Чому, на вашу думку, це працює? Яка процедура з'ясування, які тести використовувати?
Факт: Якщо кожне просте число у простому факторизації складеного числа, c, вказано лише один раз, тест на подільність для цього складеного числа такий: c|n, якщо кожен з простих множників c ділить n.
Першочерговим факторизацією для 6 є\(2 \cdot 3\). Оскільки обидва простих числа перераховані лише один раз, тест на подільність для 6 - це об'єднання тестів подільності для 2 та 3.
Першочерговим факторизацією для 15 є\(5 \cdot 3\). Оскільки обидва простих числа перераховані лише один раз, тест на подільність для 15 - це об'єднання тестів подільності для 5 та 3.
Напишіть тест на подільність для 14:
Використовуйте тест на подільність для 14, щоб побачити, що з наступного вірно. Показати роботу.
| а. 14|742 |
| б. 14|968 |
| c. 14|483 |
Першочерговим факторизацією для 20 є\(2 \cdots 2 \cdots 5\). Тест на подільність для 2, 2 та 5 не працює, оскільки 20|70 є помилковим, хоча 2|70 та 2|70 та 5|70. Чому це не працює?
Це тест на подільність для 20:20|n, якщо 4|n та 5|n. Чому, на вашу думку, це працює?
Спробуйте написати тести на подільність для кожного з наступних чисел:
| а. 12|п якщо |
| б. 18|н якщо |
Тест на подільність для складеного числа: Припустімо\(P_{1}, P_{2}, P_{3}, P_{4}, P_{5}\),... всі різні прості числа. (Ви можете розглядати\(P_{1}\) як перший простий (2),\(P_{2}\) як другий простий (3),\(P_{3}\) як третій простий (5),\(P_{4}\) як четвертий простий (7),\(P_{5}\) як п'ятий простий (11) тощо Припустимо просте факторизацію з числа, c, є\((P_{a})^{x} \cdots (P_{b})^{y} \cdots ... \cdots (P_{c})^{z}\) де\(P_{a} \neq P_{b} \neq P_{c}\) і т.д. потім c|n якщо |n І\((P_{a})^{x}\) |n І\((P_{b})^{y}\) |n і\((P_{c})^{z}\) |n і т.д.
Тест на подільність для наступних чисел проводиться шляхом їх першого факторингу.
1) Тест на подільність для 26: Починаючи з 26 =\(2 \cdots 13\): 26|п, якщо 2|п і 13|п.
2) Тест на подільність для 12: Починаючи з 12 =\(2^{2} \cdots 3\): 12|п, якщо 4|n і 3|n.
3) Тест на подільність для 24: Починаючи з 24 =\(2^{3} \cdots 3\): 24|п, якщо 8|n і 3|n.
4) Тест на подільність для 45: Починаючи з 45 =\(3^{2} \cdots 5\): 45|п, якщо 9|п і 5|п.
5) Тест на подільність для числа, c, чиє просте факторизація\(2^{3} \cdots 3^{2} \cdots 5^{2} \cdots 11\): c|n, якщо 8|n І 9|n та 25|n та 11|n
7) Тест на подільність для числа, b, просте факторизація якого\(3^{2} \cdots 5 \cdots 7^{2} \cdots 11^{2}\): b|n, якщо 9|n І 5|n та 49|n та 121|n
Напишіть тест на подільність для наступних чисел:
| а. 35: ____ |
| б. 28: ____ |
| c. 75: ____ |
| д. 56: ____ |
| e Число, c, просте множення якого дорівнює\(2^{2} \cdots 3^{3} \cdots 5^{2} \cdots 11\): ____ |
| f Число, d, просте факторизація якого дорівнює\(2^{4} \cdots 3 \cdots 5 \cdots 11\): ____ |
Ця вправа для вас, щоб подумати про те, що б ви зробили, якби хтось попросив вас знайти НАЙМЕНШИЙ загальний фактор набору чисел, а не найбільший загальний фактор.
| а. знайти найменш поширений коефіцієнт 55 і 66: ____ |
| b. знайти найменш поширений коефіцієнт 10 і 12: ____ |
| c. знайти найменш поширений коефіцієнт 1 і 8: ____ |
| d Знайти найменш поширений коефіцієнт 3, 6 і 9: ____ |
| e. знайти найменш спільний коефіцієнт m і n: ____ |
| f Як ви вважаєте корисним питанням знайти найменш поширений коефіцієнт набору чисел? Чому чи чому ні? Поясніть свою відповідь. |
| г Який найменш поширений коефіцієнт будь-якої множини чисел? ____ |
