7.3: Поділ на інших базах
- Page ID
- 66968
Вам знадобляться: Базові блоки (Матеріал карт 3 - 15)
Зараз ми попрацюємо над поділом на інші бази. Спочатку ми розділимо за допомогою повторного віднімання з фактичними базовими блоками. Пізніше ми будемо використовувати той самий алгоритм, який ми зробили в попередньому наборі вправ, щоб зробити завдання, використовуючи повторне віднімання з таблицею часткового множення, і риштування.
Вийдіть з бази три базових блоків. Ми будемо використовувати їх з повторним методом віднімання для поділу\(221_{\text{three}} \div 21_{\text{three}}\). Дивіденд є\(221_{\text{three}}\), який складається з 2 квартир, 2 лонгів і 1 одиниці. Нам потрібно з'ясувати, скільки разів ми можемо багаторазово відняти дільник\(21_{\text{three}}\), з дивідендів. Для цього ми можемо перетворити дивіденди лише на лонги та одиниці, зробивши деякі обміни, а потім сформувати якомога більше підмножин, що містять 1 довгу та 2 одиниці. Кількість сформованих підмножин - це скільки разів дільник можна було б відняти з дивідендів. Вийдіть з ваших блоків, щоб зробити цю проблему зі мною.
Крок 1: Сформуйте дивіденди в базі три. Ви повинні фактично дістати з вашої бази три блоки і робити проблеми з блоками. Я буду використовувати ініціали для базових блоків (U, L, F, B тощо), щоб показати, що відбувається. Дивіденд можна показати так:
| Ф Ф Л Л У |
Крок 2: Зробіть обмін таким чином, щоб можна було сформувати якомога більше підмножин, кожна з яких містить дільник, який становить 2 лонги та 1 одиницю. Кожну квартиру можна обміняти на 3 лонги, щоб отримати:
| Л Л Л Л Л Л Л Л |
Потім один з лонгів можна обміняти на 3 одиниці, щоб отримати L L L L L L L L L U U U U. Давайте подивимося, чи зможемо ми відняти деякі рівні підмножини 2 лонгів і 1 одиницю з дивідендів. Коли ви виймаєте кожні 2 лонги та одиницю, сформуйте їх у підмножині.
Я можу взяти і сформувати 3 рівні підмножини 2 лонгів і 1 одиницю кожен з дивідендів. У дивіденді залишається одна довга і 1 одиниця. Сформовані підмножини виглядають наступним чином:
| ЛЛУ | ЛЛУ | ЛЛУ |
Частина, що залишилася в дивіденді, яка є залишком, виглядає так:
| ЛУ |
Крок 3: Кожна рівна підмножина з 2 лонгів і 1 одиниця, яка була віднімана з дивідендів, вважається 1 для частки. Дайте собі одиницю для кожної рівної підмножини, яку ви сформували, це частка. Довга і одиниця, що залишилася, є залишком, оскільки вона менше, ніж дільник.
| Коефіцієнт: U U U | Залишок: L U |
Крок 4: У частці та/або залишку зробіть будь-які обміни, необхідні, щоб частка та залишок могли бути записані в базі три.
| Частка: L | Залишок: L U |
Крок 5: Напишіть частку та залишок у базі три:\(10_{\text{three}}r. 11_{\text{three}}\).
Тому,\(221_{\text{three}} \div 21_{\text{three}} = 10_{\text{three}}r. 11_{\text{three}}\)
Крок 6: Перевірте відповідь. Це показано праворуч.
Слідуючи прикладу на попередній сторінці, виконайте наступний поділ крок за кроком. Використовуйте базові три блоки, щоб зробити цю вправу. Ви можете або використовувати ініціали, або намалювати фотографії блоків, щоб показати, як ви робите поділ.
Виконайте наступне поділ:\(222_{\text{three}} \div 12_{\text{three}}\)
а Сформувати дивіденди в базі три. Намалюйте картину того, як виглядає дивіденд:
b Зробіть обмін таким чином, щоб можна було сформувати якомога більше підмножин, кожна з яких містить дільник, який становить 1 довгий і 2 одиниці. Відніміть деякі рівні підмножини 1 long і 2 одиниці з дивідендів. Коли ви виймаєте кожну довжину і 2 одиниці, сформуйте їх у підмножині.Намалюйте картину всіх рівних підмножин, які ви змогли сформувати, віднімаючи з дивідендів, потім намалюйте окрему картину того, що залишилося в дивіденді, який буде залишком (це повинно бути менше 1 довгої і 2 одиниці).
i) Показати всі сформовані рівні підмножини:
ii) Залишок:
c Для кожної з рівних підмножин 1 довга і 2 одиниці, яка була віднімана з дивідендів і сформована (показана в b.i.), дайте собі одиницю — це частка. Намалюйте малюнок частки в перерахунку на одиниці:
d У частці (частина c) та/або залишок (частина b.ii), зробити будь-які обміни необхідні, щоб частка і залишок можуть бути записані в базі три. Намалюйте картину того, як виглядає частка та залишок після здійснення будь-яких обмінів можливими.
| Частка: | Залишок: |
Перевірка:\(\begin{aligned} 21_{\text{three}} \\ \underline{\times 10_{\text{three}}} \\ 210_{\text{three}} \\ \underline{+ 11_{\text{three}}} \\ 221_{\text{three}} \end{aligned}\)
е. запишіть частку і залишок в базі три: ____________________________
f Перевірте відповідь.
Використовуйте базові блоки в зазначених базах, щоб знайти частку та залишок для кожної задачі. Потім перевірте свою відповідь в наданій базі. Покажіть свою роботу. Ви можете множити за допомогою будь-якого алгоритму множення, який ви віддаєте перевагу - ви можете спробувати грати.
|
а.\(1204_{\text{five}} \div 42_{\text{five}}\) = Перевірка: |
с.\(1345_{\text{six}} \div 25_{\text{six}}\) = Перевірка: |
|
б.\(323_{\text{four}} \div 23_{\text{four}}\) = Перевірка: |
д.\(11111_{\text{two}} \div 101_{\text{two}}\) = Перевірка: |
Можливо, ви помітили в частинами c і d, що вам довелося зробити багато паль, і що повторне віднімання було дещо стомлюючим, коли ви могли відняти лише одну підмножину дільника з дивідендів за раз. Тут корисно використовувати ідею, що тривалий час дільник схожий на множення на 10 в базовій десятці. Пам'ятайте, що 10b - це довгий для деякої бази, б, наприклад, коли ви помножите 25 разів 10, ви отримаєте 250. У базовій шести\(25_{\text{six}}\) означає 2 лонги і 5 одиниць. Коли ви помножите це на довгий (\(10_{\text{six}}\)), ви отримуєте\(250_{\text{six}}\) 2 квартири і 5 лонгів - кожен шматок зміщується вгору значення місця. Ми можемо використовувати це у вправі 2c, щоб зробити віднімання швидше. Ми зробимо вправу 2c, використовуючи цю ідею на наступній сторінці.
Вправа 2с,\(1345_{\text{six}} \div 25_{\text{six}}\), може бути виконана за допомогою більш ефективного методу. Ось кроки:
Намалюйте малюнок дивідендів\(1345_{\text{six}}\), використовуючи блоки Base Six.
| Б Ф Ф Л Л Л Л У У У У |
Ви хочете, щоб відняти якомога більше підмножин дільника\(25_{\text{six}}\), з дивідендів, як ви можете. Це займе багато кроків. Вам доведеться розбити блок і три квартири на безліч лонгів і одиниць. Тепер\(25_{\text{six}}\), означає 2 лонги і 5 одиниць. Якщо ви помножили це на довгий, ви б\(250_{\text{six}}\), що є 2 квартири і 5 лонг. Якщо ви віднімали 2 квартири та 5 лонгів з дивідендів одночасно, це було б так само, як віднімання 2 лонгів та 5 одиниць з дивідендів шість разів! А можна відняти відразу 2 квартири і 5 лонг.
Давайте торгуємо деякими частинами в дивіденді на менші шматки, так що можна взяти віднімання і зробити підмножини з 2 квартир і 5 лонгів. Я почав з торгівлі блоком на 6 квартир і дві квартири в протягом 12 лонгів:
| Ф Ф Ф Ф Ф Ф Л Л Л Л Л Л Л Л Л Л Л Л Л Л Л Л Л У У У У |
Тепер я сформую якомога більше підмножин 2 квартир і 5 лонгів, наскільки це можливо.
| Ф Л Л Л Л Л Л | Ф Л Л Л Л Л Л | Ф Л Л Л Л Л Л |
У мене все ще залишилося F L U U U U у дивідендах, і я не можу взяти більше підмножин 2 квартир і 5 лонг. Так що тепер, я намагаюся відняти підмножини дільника від того, що залишилося в дивіденді. Знову ж таки, мені потрібно зробити кілька торгів. Я буду торгувати квартира на 5 лонгів і 6 одиниць, так що у мене є:
| Л Л Л Л Л Л Л У У У У У У У У У У |
Можна сформувати дві підмножини:
| Л Л У У У У | Л Л У У У У |
Все, що залишилося в дивіденді - це одиниця і 2 лонги, що менше дільника, і є залишком. Таким чином, решта, LLU, є\(21_{\text{six}}\).
Тепер, ми повинні з'ясувати частку. Перші 3 підмножини, які я сформував, були кожен довгий раз дільник, так що для частки, я поклав в довгий для кожного з підмножин утворених. Я поставив одиницю для кожної з наступних двох підмножин, які я сформував. Так що у мене є 3 лонг і 2 одиниці для частки, і ніяких обмінів не потрібно робити.
Коефіцієнт дорівнює L L L U U, або\(32_{\text{six}}\), а залишок -\(21_{\text{six}}\).
Тому\(1345_{\text{six}} \div 25_{\text{six}} = 32_{\text{six}}\) р.\(21_{\text{six}}\)
Ви повинні були отримати ту ж відповідь, коли ви зробили вправу 2c, але ви б віднімали і сформували 13 підмножин дільника, а потім торгували 13 одиниць в для відповіді в базовій шести.
(До речі, якщо дільник\(25_{\text{six}}\), був помножений на квартиру, у вас буде 2 будинки і 5 квартир, що більше, ніж дивіденд, так що ми не можемо взяти, що багато дільник геть в один час. Отже, ми починаємо з віднімання підмножин довгих разів дільник, по одному за раз.)
Розділіть наступне за допомогою базових блоків. Ви можете використовувати метод, описаний на попередній сторінці, або відняти одну підмножину дільника за раз. Поясніть або намалюйте зображення з блоками, щоб показати, як ви зробили проблему. Перевірте свої відповіді за допомогою будь-якого алгоритму множення.
|
а.\(1046_{\text{seven}} \div 31_{\text{seven}}\) = _____________________________________________ Перевірка: |
|
б.\(10021_{\text{three}} \div 22_{\text{three}}\) = _____________________________________________ Перевірка: |
Тепер ми будемо працювати над діленням в різних базах, використовуючи той же повторюваний алгоритм віднімання, який ми зробили в наборі вправ 2. Оскільки більшість, якщо не всі з нас недостатньо знайомі з різними основами для оцінки в нашій голові, складання таблиці часткового множення стає надзвичайно корисним для цих проблем.
Оскільки кожна база має різну кількість цифр, ми можемо вибрати метод подвоєння або деяку часткову таблицю для більших основ, таких як база 11, 12 та 13. Для менших баз ви можете розглянути можливість створення повної таблиці. У базовій п'ятій, вам доведеться тільки з'ясувати 2, 3 і 4 рази дільник (так як 4 є найвищою цифрою в базовій п'ятій). Вивчіть наступні приклади використання методу риштування в інших базах.
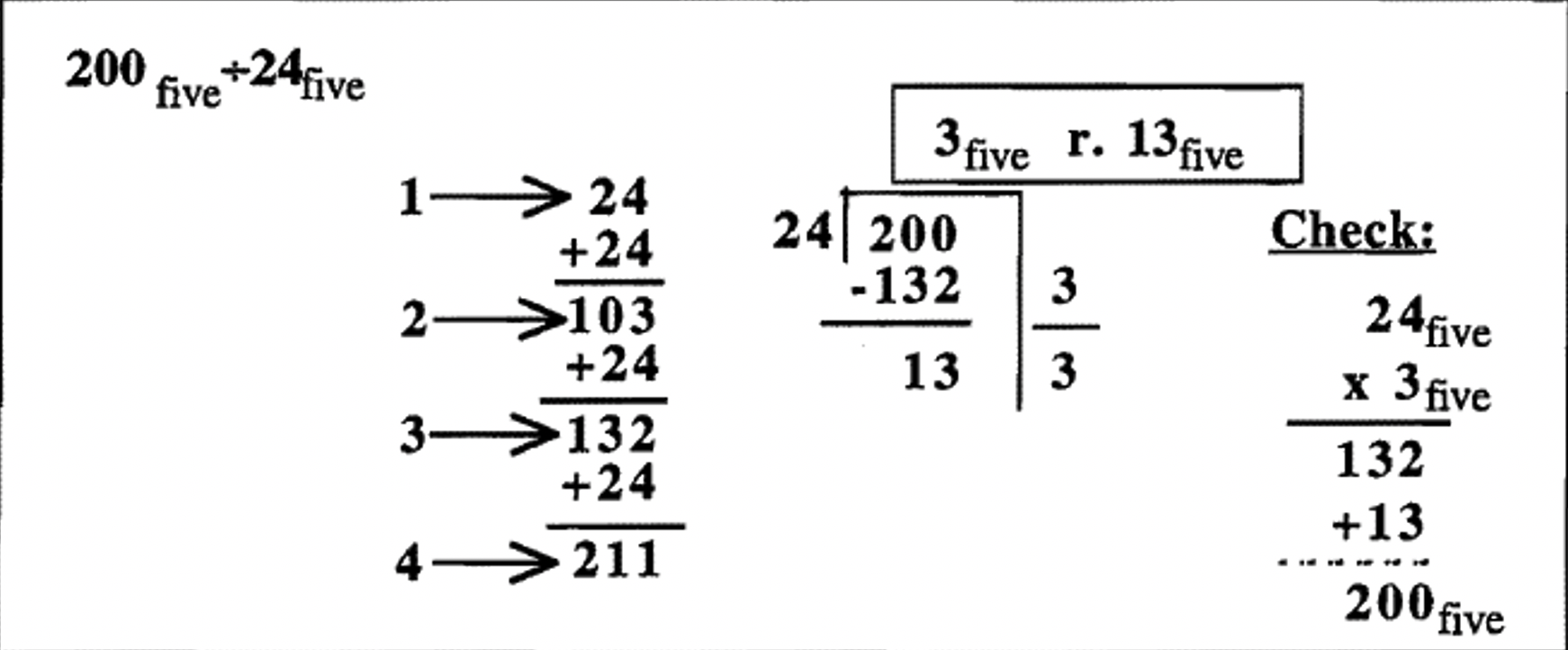
Задача поділу в п'ятій базі:\(200_{\text{five}} \div 24_{\text{five}}\). Я залишаю від написання «п'ять» крім відповіді (в коробці) і чека. Ви повинні бути дуже обережними, щоб пам'ятати, що ви перебуваєте в базовій п'ятій, коли ви додаєте (підготовча робота на початку та додавання в кінці перевірки, коли ви додаєте залишок), віднімання (повторне віднімання) та множення (у чеку). Для перевірки ви можете використовувати метод решітки або будь-який інший спосіб, який ви віддаєте перевагу.
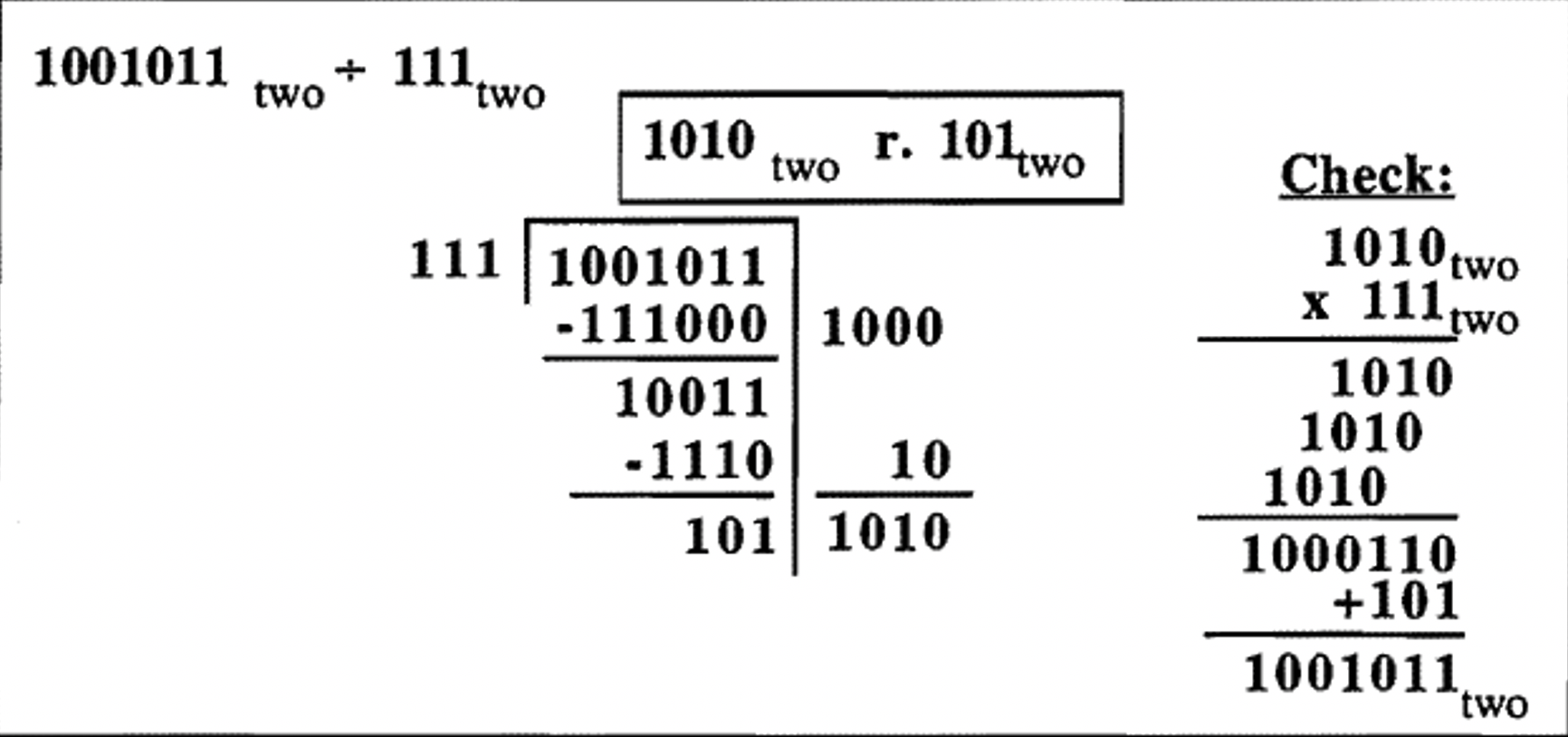
Задача поділу в базі дві:\(1001011_{\text{two}} \div 111_{\text{two}}\). Там дійсно немає підготовчої роботи тут, тому що єдиними цифрами в базі два є 0 і 1.
Для прикладів 3 і 4 я вирішив зробити інший вид часткової таблиці множення для кожного.
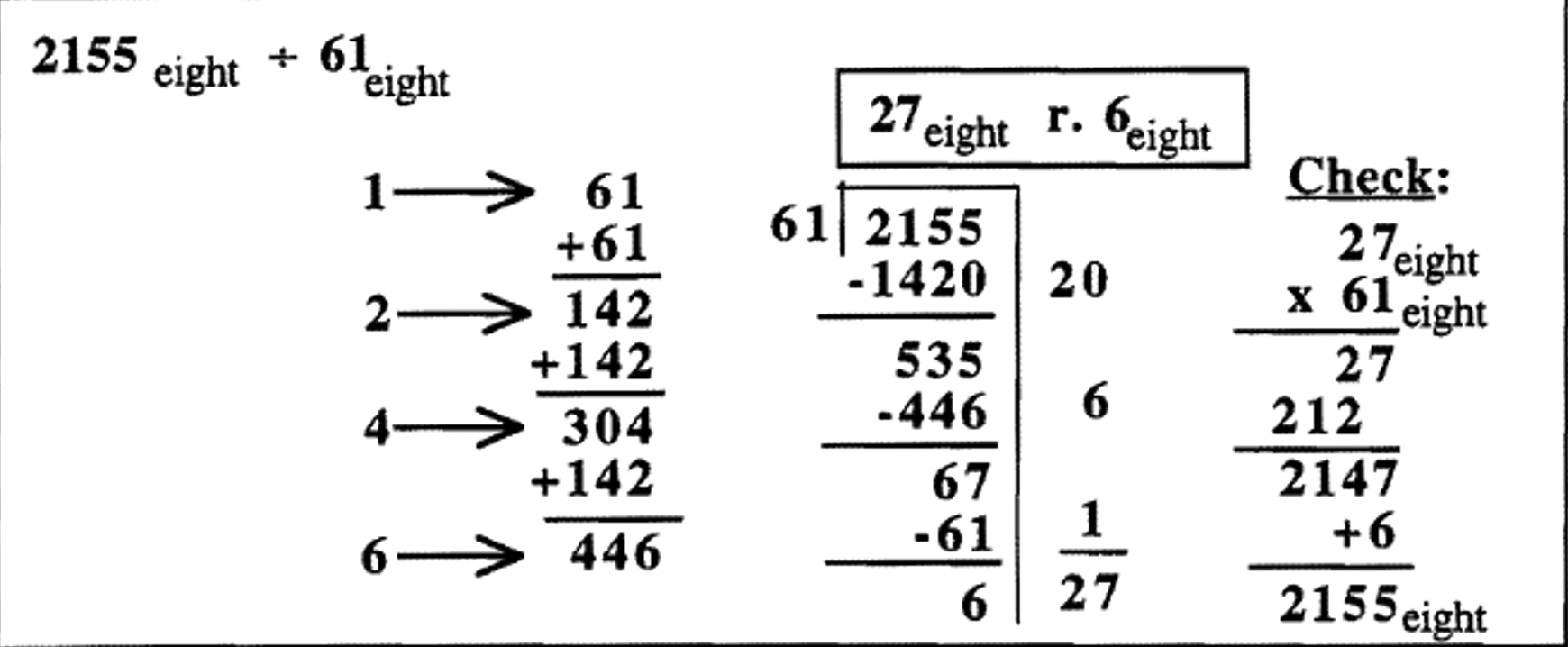
Задача поділу в базовій вісімці:\(2155_{\text{eight}} \div 61_{\text{eight}}\). Оскільки це проблема в базовій вісім, я вирішив зробити часткову таблицю, щоб з'ясувати дільник раз 1, 2, 4 і 6. Інша людина може вибрати, щоб зробити таблицю тільки для 1, 2 і 4. Пам'ятайте, що 7 - це найвища цифра в базовій вісімці. Ще один студент може зробити повну таблицю для всіх цифр в базовій вісім: 1, 2, 3, 4, 5, 6 і 7.
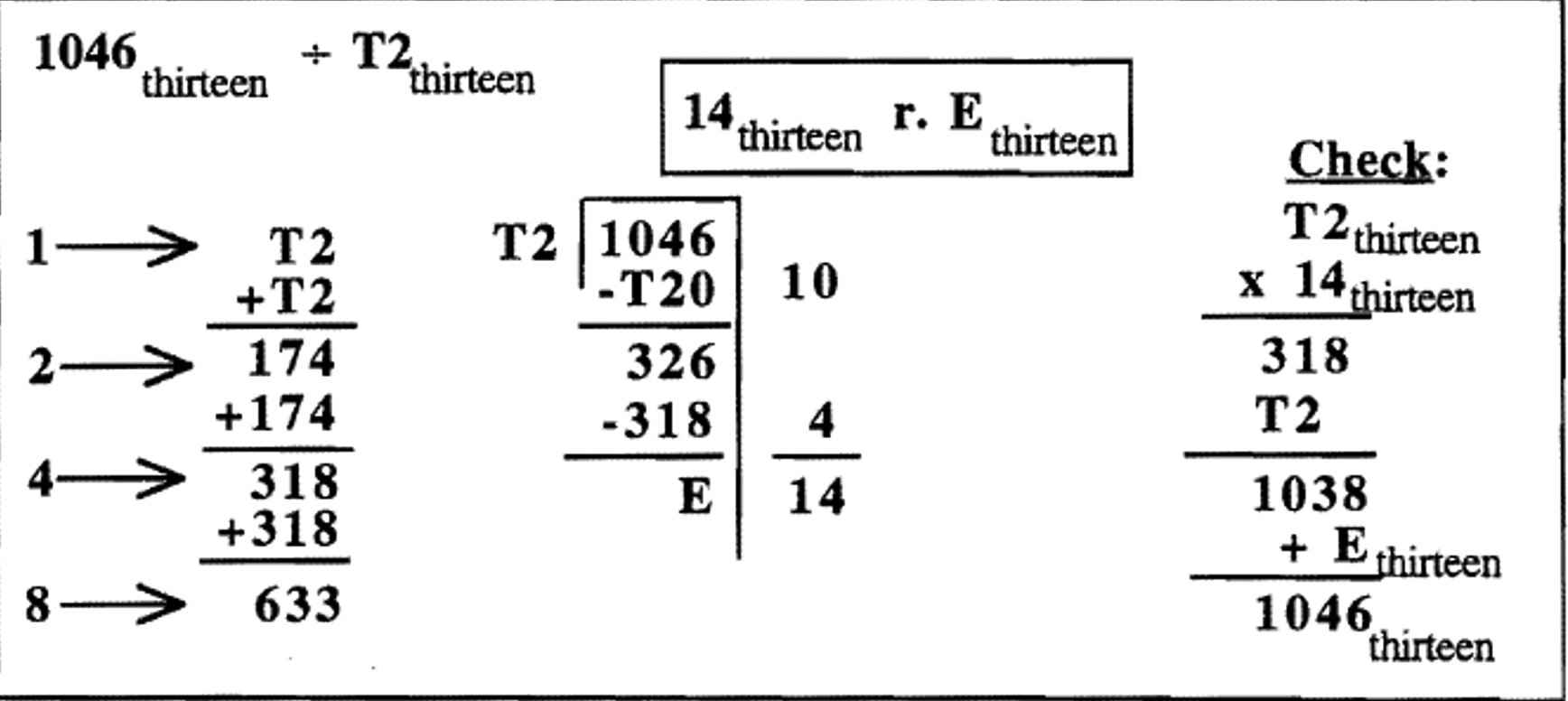
Задача поділу в базі тринадцять:\(1046_{\text{thirteen}} \div T2_{\text{thirteen}}\). Оскільки це проблема в базі тринадцять, я вирішив зробити часткову таблицю, щоб з'ясувати дільник раз 1, 2, 4 і 8. Пам'ятайте, що W - найвища цифра в базовій вісімці. Інша людина може вибрати, щоб зробити таблицю для 1, 2, 4, 6, 8, T і W. Пам'ятайте, що W є найвищою цифрою в базі тринадцяти. Інший студент може скласти повну таблицю для всіх цифр в базі тринадцять, але це багато підготовчої роботи, яка зазвичай не окупається.
Переконайтеся, що ви практикуєте попередні чотири приклади, перш ніж виконувати вправи, які слідують на наступних сторінках.
Для кожної з задач поділу в решті частини цього розділу покажіть свою роботу, використовуючи модель, подібну до останніх чотирьох прикладів. Спочатку складіть часткову або повну таблицю множення (підготовка до ділення за допомогою повторного віднімання). Потім розділіть за допомогою методу риштування з повторним методом віднімання. Напишіть свою відповідь в поле над риштуванням. Потім перевірте свою відповідь, помноживши дільник на частку і додавши залишок. Переконайтеся, що ви звертаєте пильну увагу на те, в якій базі ви працюєте, коли ви додаєте, віднімаєте та/або множите в цій базі. Не забудьте написати базу, коли ви пишете частку та залишок.
\(222_{\text{three}} \div 12_{\text{three}}\)
\(1204_{\text{five}} \div 42_{\text{five}}\)
\(323_{\text{four}} \div 23_{\text{four}}\)
\(1345_{\text{six}} \div 25_{\text{six}}\)
\(11111_{\text{two}} \div 101_{\text{two}}\)
\(1046_{\text{seven}} \div 31_{\text{seven}}\)
\(10021_{\text{three}} \div 22_{\text{three}}\)
\(200_{\text{five}} \div 3_{\text{five}}\)
\(1001011_{\text{two}} \div 1010_{\text{two}}\)
\(2155_{\text{eight}} \div 27_{\text{eight}}\)
\(1046_{\text{thirteen}} \div 14_{\text{thirteen}}\)
\(101\text{E}_{\text{twelve}} \div 54_{\text{twelve}}\)
