7.2: Алгоритми поділу
- Page ID
- 66955
Як ми бачили, ділення можна розглядати як протилежне множенню.
Ще один спосіб подумати про це - повторне віднімання.
Давайте зробимо ПОДІЛ Легкий Шляхом!
Правильно. Ділення - це дійсно просто «повторне віднімання». Якщо вас попросять розділити 17 на 3\(17 \div 3\), що написано, ви повинні з'ясувати, скільки 3 можна відняти від 17. Ви, напевно, вже знаєте відповідь 5 р. 2, але давайте подивимося, як це працює, підрахувавши, скільки разів 3 можна відняти від 17. Подивіться на роботу нижче. Показано три різні способи. Ви робите риштування (схоже на кат) і відстежуєте, скільки 3 ви віднімаєте на кожному кроці праворуч від риштування. У першому віднімається 3 за один раз, і загалом було віднімано п'ять 3. У другому віднімаються перші два 3, потім ще 1, потім ще 2, в цілому п'ять 3 віднімається. У третьому, чотири 3 віднімаються, а потім ще 1, знову на загальну суму п'ять 3 віднімається. Кожен раз, коли ви віднімаєте, дивіться, яке число залишилося. Якщо це 3 або більше, ви можете відняти ще деякі 3, Але коли ви отримаєте число менше 3, ви знаєте, що 3 не можна відняти більше, так що це ваш залишок. Для цієї проблеми 2 була залишок. Вам потрібно порахувати, скільки 3 ви віднімали. Праворуч від риштування, ви пишете, скільки 3 ви віднімаєте, коли йдете разом. Просто додайте ці цифри, щоб дізнатися, скільки 3 ви віднімали. Відповідь на проблему полягає в тому, скільки 3-х ви віднімали, а потім потрібно ще й написати залишок. В даному випадку,\(17 \div 3 = 5\) р. 2. Завжди перевіряйте свою відповідь, множивши дільник (3) на частку (5) та додаючи залишок (2):\(3 \times 5 + 2 = 15 + 2 = 17\). Це перевіряє!
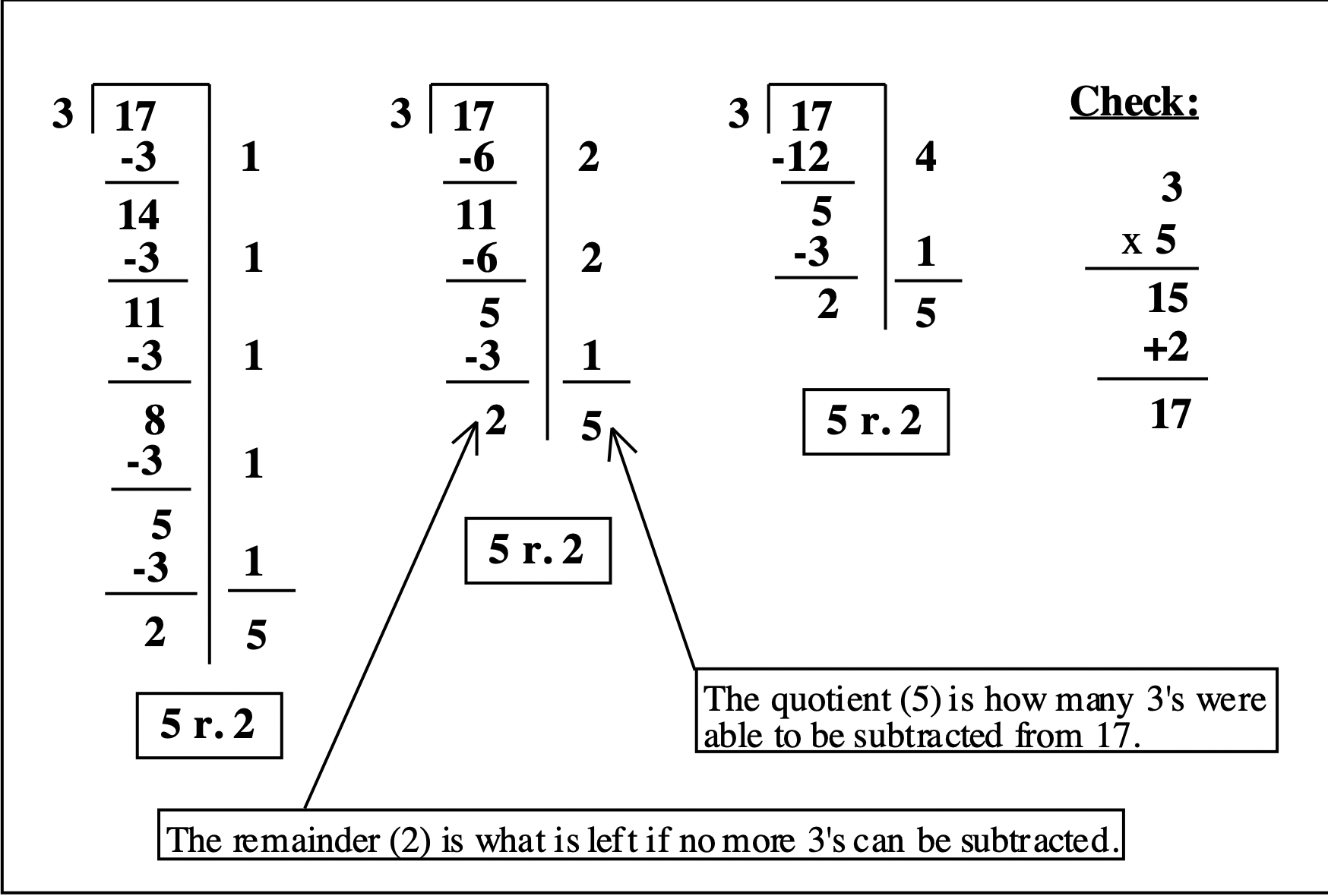
Робити довгий поділ великими числами часто важко, тому що доводиться множитися в голові, і легко помилитися. Але, використовуючи цей новий метод повторного віднімання, поряд з частковим множенням, яке ви складаєте заздалегідь, використовуючи повторне додавання, вам ніколи не доведеться множити в голові (або множити взагалі), і вам ніколи не доведеться здогадуватися, скільки разів одне число «переходить» в інше число. Цей метод займає трохи більше паперу, але він полегшує проблему і він практично безглуздий. Багато людей не люблять робити довгий поділ, тому що важко завжди вгадати точне правильне число, а іноді вони отримують головний біль від занадто важкого мислення. Ми збираємося усунути цю проблему. Важливим є те, що ви знаєте, що означає поділ (повторне віднімання), ви знаєте, як отримати правильну відповідь, використовуючи метод, який має сенс для вас, і ви знаєте, як перевірити свою відповідь, щоб переконатися, що це правильно.
Гаразд, припустимо, вам довелося зробити цю проблему поділу:\(361 \div 53\).
ЮК! Це не схоже на будь-яку забаву. Власне, все це запитує, скільки 53 можна відняти від 361. Ми можемо відняти 53 по одному, але це може зайняти багато часу. Ми можемо вирішити відняти більше одного 53 за раз.
Перш ніж робити ділення, давайте зробимо швидку таблицю часткового множення для 53, використовуючи ПОВТОРНЕ ДОДАВАННЯ! Ця таблиця - ваша підготовча робота для поділу. Простий спосіб скласти часткову таблицю множення для 53 без коли-небудь множення тягне за собою подвоєння чисел. Ми це знаємо\(1 \times 53 = 53\). Щоб з'ясувати\(2 \times 53\), просто додайте два 53 разом. Два 53, додані до двох ще 53, дорівнювало б чотирьом 53, або\(4 \times 53\). Чотири 53 додані до чотирьох ще 53 дорівнювало б восьми 53, або\(8 \times 53\). Гаразд, так як ви це показуєте? Почніть з одного 53 і подвоюйте його, щоб знайти два 53. Подвойте це число, щоб знайти чотири 53. Подвойте це число, щоб знайти вісім 53. Подивіться на ліву частину поля, показаного нижче. Подивіться, як існує 1, що вказує на 53, що означає\(1 \times 53\). Якщо ви подвоїте 53, (53 + 53), то тепер ви знаєте\(2 \times 53 = 106\), так що 2 бали до 106. Якщо ви подвоїте це (106 + 106), ви тепер знаєте\(4 \times 53 = 212\), так що 4 бали до 212. І якщо ви подвоїти це число (212 + 212), то ви тепер знаєте\(8 \times 53 = 424\), так що 8 балів до 424. Хіба це не простий спосіб знайти\(8 \times 53\)? Але найкрутіше те, що ви також знаєте\(1 \times 53, 2 \times 53, 4 \times 53,\) І\(8 \times 53\)! Це корисно знати, щоб зробити довгий поділ. Замість того, щоб вгадувати, скільки разів 53 «переходить» 361, відзначимо, скільки 53 можна відняти від 361 (недооцінка - це нормально). Ніякого множення не потрібно робити і в голові! Поле праворуч показує, як використовувати повторне віднімання для виконання завдання ділення:\(361 \div 53\). Спочатку складіть часткову таблицю множення. Потім напишіть проблему поділу за допомогою риштування. Подивіться на таблицю множення і виберіть найбільше число, яке ви можете відняти від 361, тобто 212. Відніміть 212 з 361 і напишіть 4 праворуч, тому що ви щойно віднімали 4 53, Найбільше число, яке ви можете відняти від 149, - 106. Якщо ви робите це, ви віднімали 2 більше 53, так що напишіть 2 праворуч. Після віднімання залишається 43 і не можна відняти більше 53. Тому 43 - це залишок. Додайте цифри праворуч, щоб побачити, скільки 53 ви віднімали. Відповідь - 6 р. 43. Для перевірки множимо\(53 \times 6\) і додаємо 43. Відповідь 361.
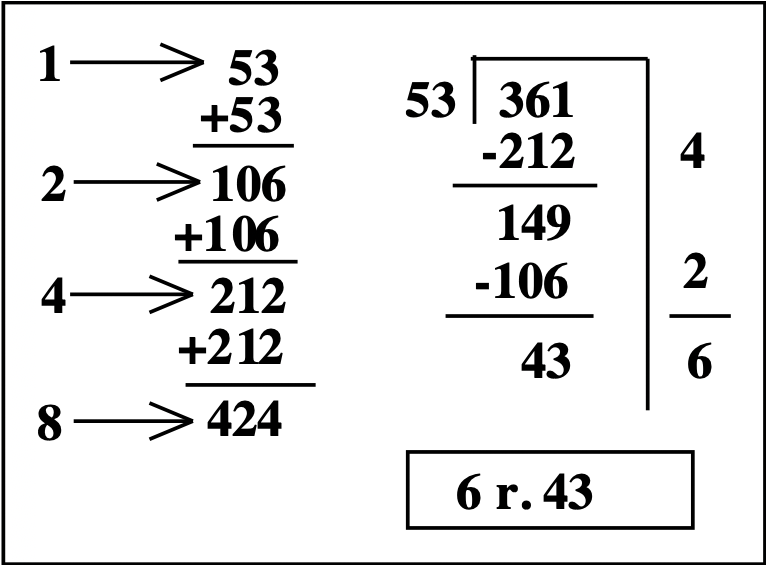
P.S., Ви можете помножити 53 рази 6, додавши 106 + 106 + 106, так як це два 53 складено разом 3 рази, що шість 53!!!
Ось ще кілька прикладів для вивчення. Спочатку складається таблиця часткового множення. Ця підготовча робота, яка включає в себе кілька доповнень, робить поділ набагато простіше. Потім завдання виконується за допомогою повторного віднімання (за допомогою таблиці часткового множення) за допомогою ешафот. Після складання того, скільки разів дільник був відніманий з дивіденду (числа праворуч від риштування), відповідь (частка і залишок) записується в поле вище завдання. Нарешті, показується перевірка. Крім того, перевірте, щоб залишок був меншим за дільник.
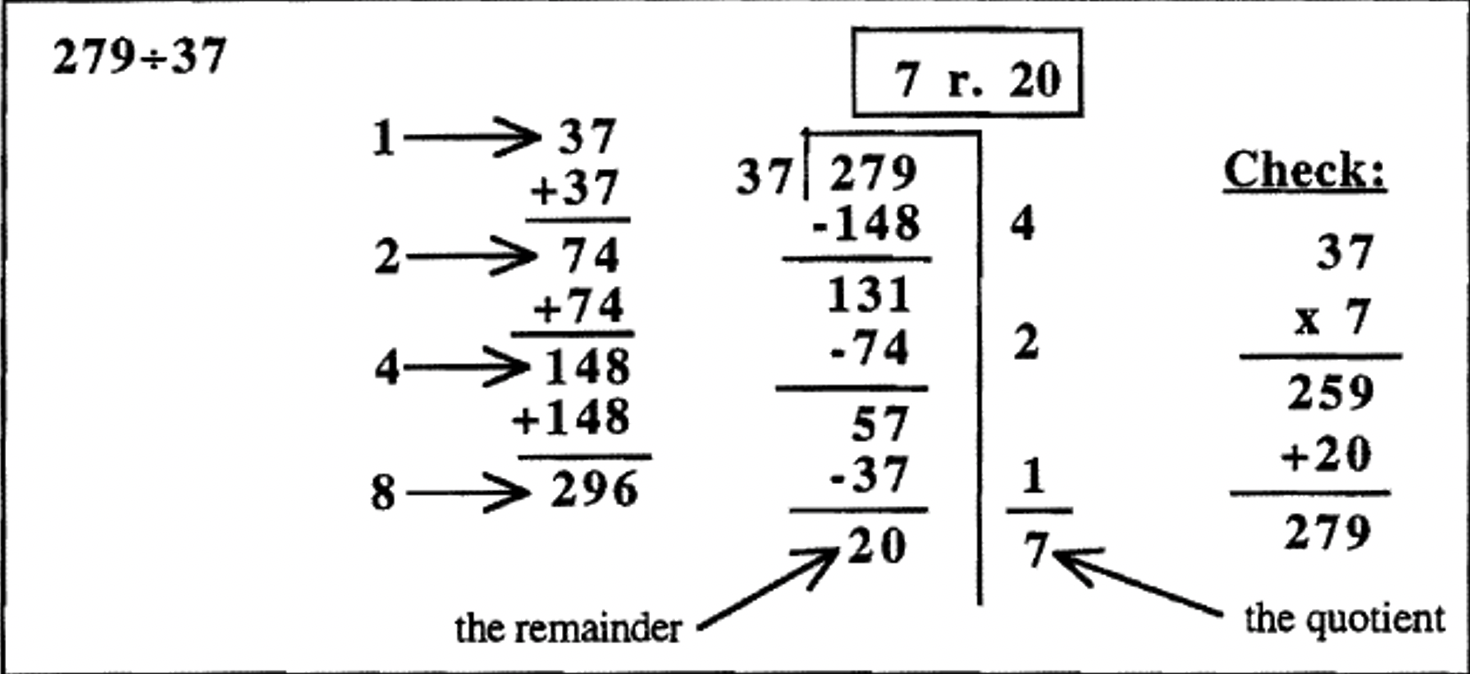
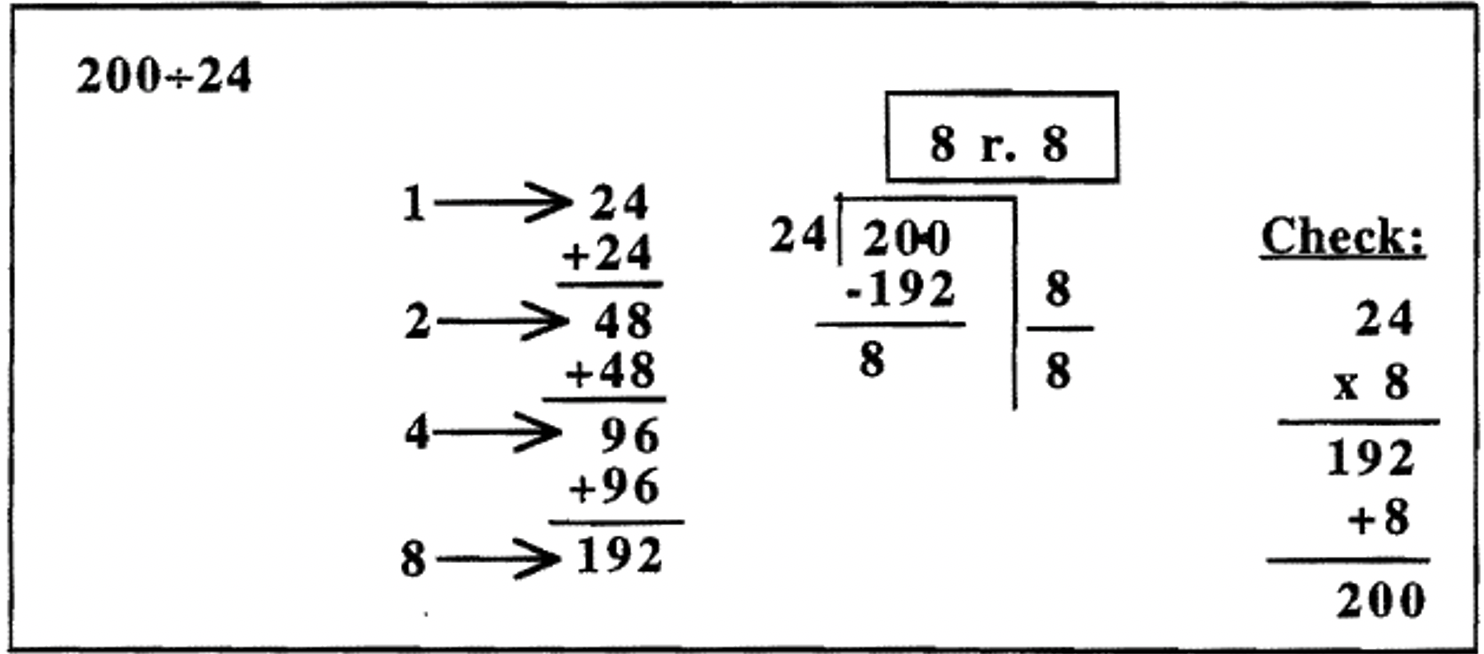
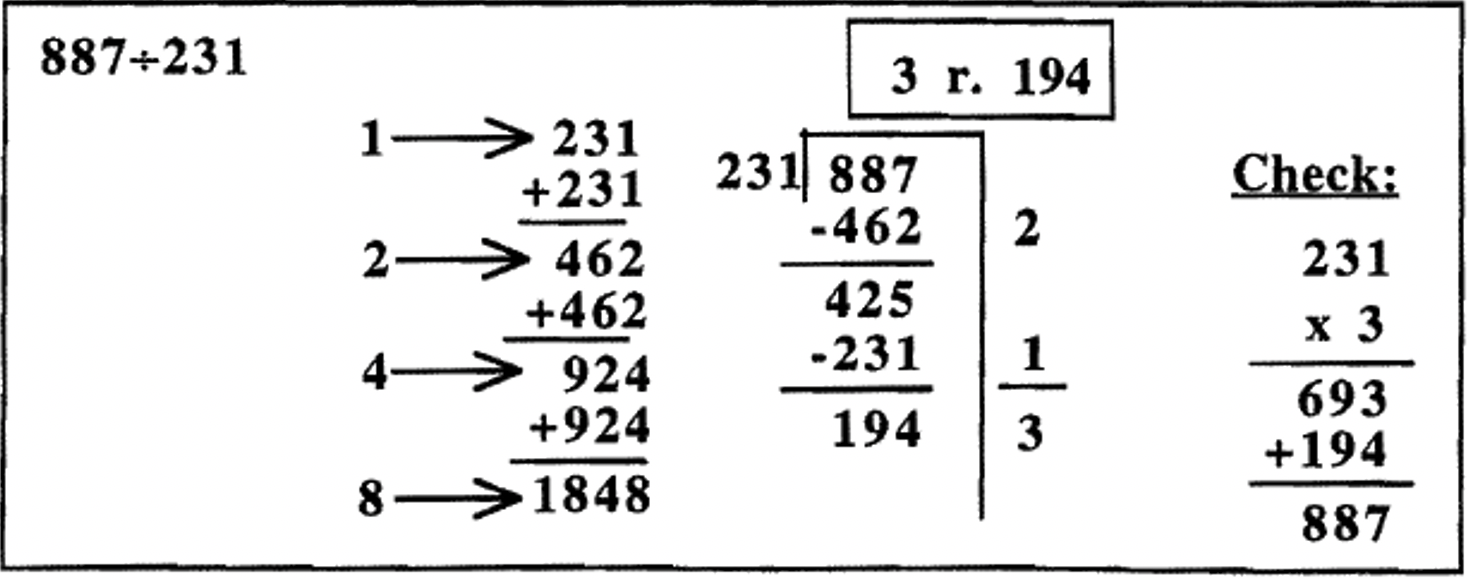
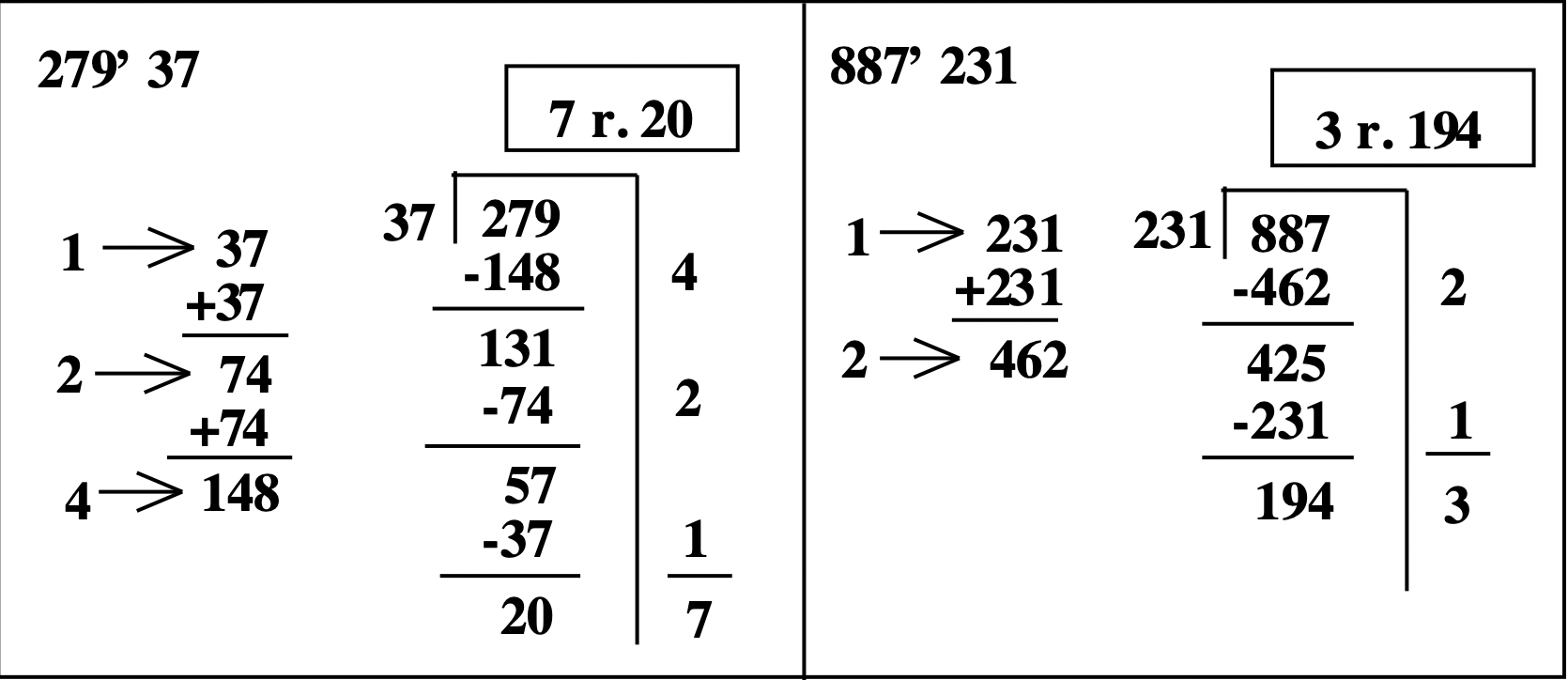
У прикладах до цих пір всі частки були менше 10. Можна продовжити подвоєння дільника в таблиці часткового множення, так що ви можете знайти дільник разів будь-якої потужності 2 - 1, 2, 4, 8, 16, 32, 64 тощо Ви б припинили подвоєння, якщо помітите, що подвоєння ще раз дає число більше, ніж частка. Насправді, у першому прикладі на попередній сторінці\(279 \div 37\), я дійсно не повинен був подвоїти 148, щоб з'ясувати\(8 \times 37\), так як подвоєння 148 дає мені число більше, ніж 279. У третьому прикладі мені не довелося подвоювати 462, щоб з'ясувати\(4 \times 231\), оскільки подвоєння 462 дає число більше 887.\(887 \div 231\) Проблеми можна було трохи скоротити, якби я помітив, що завчасно. Вони виглядали б так (перевірка опущена).
Гаразд, тепер, коли ви вивчили деякі приклади, настав час спробувати використовувати цей метод. Перші чотири проблеми - це ті ж саме ті, що і в попередніх прикладах. Якщо ви застрягли, озирніться на них і скопіюйте, як я їх зробив на іншому аркуші паперу. Потім спробуйте ще раз.
Для кожної задачі ділення виконайте підготовчу роботу, використовуючи метод подвоєння (подвійний, наскільки це необхідно), щоб спочатку скласти таблицю часткового множення. Потім намалюйте риштування та використовуйте повторне віднімання, щоб зробити кожне поділ. Коли ви закінчите, переконайтеся, що залишок менше, ніж дільник. Потім перевірте відповідь. Всі роботи повинні бути показані в передбаченому просторі. Після перевірки напишіть відповідь на простір, надане на початку завдання.
|
а.\(361 \div 53\) = _______________
|
|||
|
б.\(279 \div 37\) = _______________
|
|||
|
с.\(200 \div 24\) = ___________________
|
|||
|
д.\(887 \div 231\) = ______________
|
|||
|
е.\(415 \div 72\) = _______________
|
|||
|
ф.\(1235 \div 214\) = _____________
|
|||
|
г.\(3128 \div 321\) = _____________
|
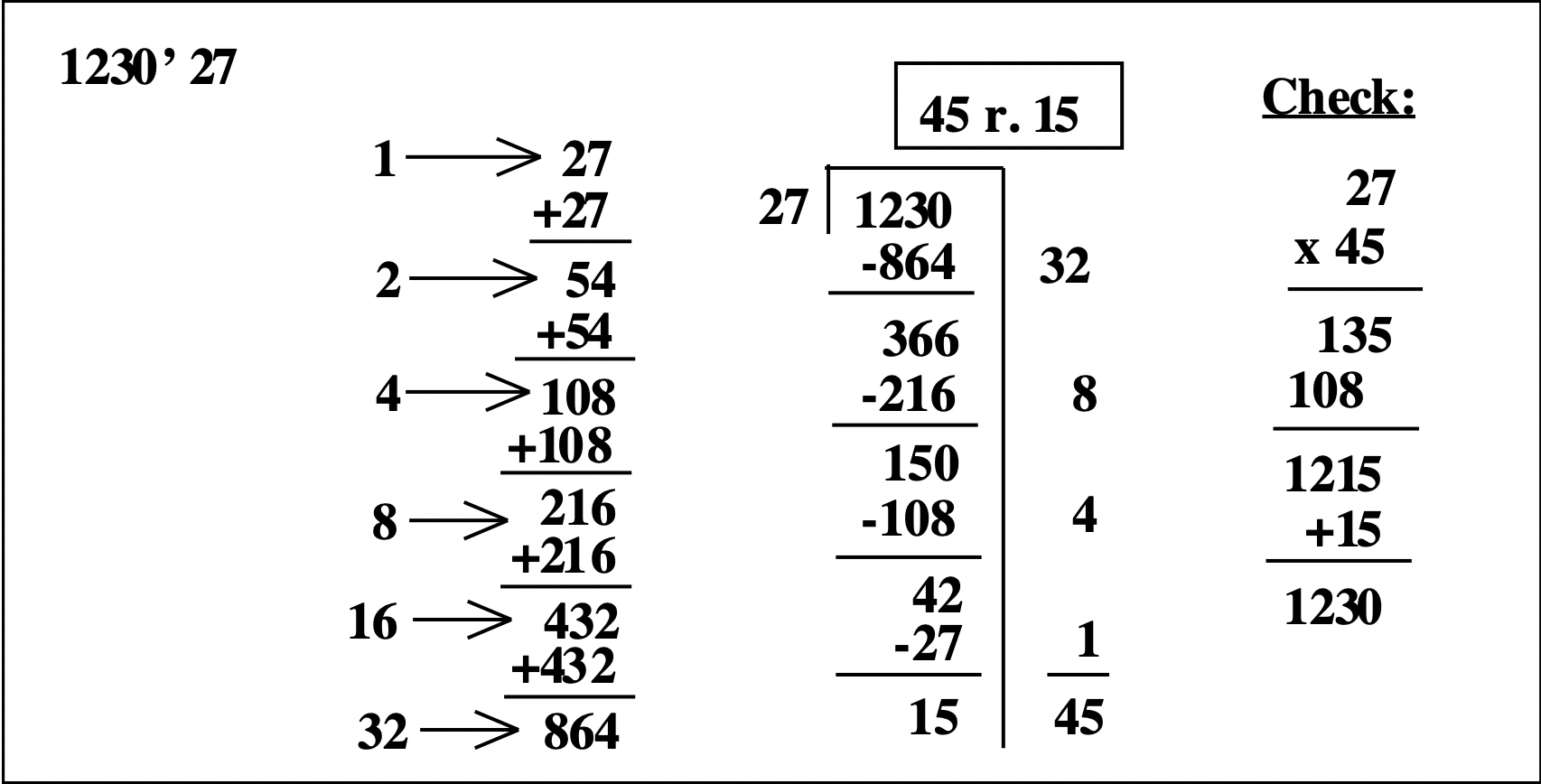
Нижче наведено приклад, який показує, що подвоєння може продовжуватися таким чином. Ви припиняєте подвоєння, якщо ще один двійник дає число більше, ніж частка. Нижче наведено\(1230 \div 27\).
Я дякую і віддячую моєму синові, Якобу, цим методом подвоєння, щоб з'ясувати більше восьми разів дільник. Я завжди використовував метод, який використовував використання значень місця і кратні 10, які ми отримаємо після того, як зробити кілька таким чином. Якоб, дев'ять років і в четвертому класі, ненавидів довгий поділ, тому що це не мало сенсу для нього, і мав проблеми з «ворожінням». Перш ніж я зміг показати йому свій метод, де ви використовуєте метод подвоєння, щоб зробити часткову таблицю множення лише до 8 разів дільник, він зробив усі проблеми, як показано вище. Це нарешті мало сенс для нього, і він зробив їх все правильно!!! Це відкрило для мене абсолютно новий спосіб мислення. Діти та студенти можуть бути чудовими новаторами! Це чудово, коли ви отримуєте можливість досліджувати та відкривати самостійно, і знайти власне рішення, яке має сенс. Ми повинні пам'ятати, що немає нічого священного ні в одному алгоритмі поділу, ні в будь-якій іншій операції.
Гаразд, настав час спробувати ще кілька проблем, використовуючи метод подвоєння, де частка більше 10. Перша проблема така ж точна, що і вище. Якщо ви застрягли, озирніться на нього і скопіюйте, як я це зробив на іншому аркуші паперу. Потім спробуйте ще раз.
Для кожної задачі ділення (починаючи з наступної сторінки) використовуйте метод подвоєння (подвійний, наскільки це необхідно), щоб скласти таблицю часткового множення. Потім намалюйте риштування та використовуйте повторне віднімання, щоб зробити кожне поділ. Потім перевірте відповідь і переконайтеся, що залишок менше дивідендів. Всі роботи повинні бути показані. Після перевірки напишіть відповідь на простір, надане на початку завдання.
Перевірка:\(\begin{aligned} 27 \\ \underline{\times 45} \\ 1215 \\ \underline{+ 15} \\ 1230 \end{aligned}\)
Для перевірки відповіді може бути використаний калькулятор. Наприклад, щоб перевірити, що 45 р. 15 є правильною відповіддю\(1230 \div 27\), потрібно помножити 27 на 45 і додати 15. Відповідь має бути 1230. Ви можете використовувати калькулятор, щоб зробити множення і додавання, але запишіть кроки.. Це виглядало б так, як показано праворуч.
|
а.\(1230 \div 27\) = ______________
|
|||
|
б.\(603 \div 48\) = _______________
|
|||
|
с.\(1346 \div 41\) = ______________
|
|||
|
д.\(3512 \div 43\) = ______________
|
Можливо, ви помітили, що таблиця часткового множення може стати довгою, якщо вам доведеться продовжувати подвоєння на деякий час. Крім того, не так просто скласти цифри праворуч від риштування. Інший підхід полягає в тому, щоб скористатися тим, що множивши ціле число на 10 або 100 і т.д., просто додає нулі в кінець числа. Наприклад, якщо ви знаєте 53 рази 2 106, то 53 рази 20 1060, а 53 рази 200 10600. Ми будемо використовувати цей факт, щоб розділити за допомогою повторного віднімання, коли частка більше 10.
Озирніться назад на останню проблему, яку ви зробили у вправі 2:\(3512 \div 43\). Довелося подвоїтися, поки не з'ясували, що 64 рази 43 було. У вікні внизу цієї сторінки знаходиться інший спосіб виконання тієї ж проблеми. Пояснення та кроки знаходяться на цій та наступній сторінці.
Крок 1: Використовуйте подвоєння, щоб скласти таблицю часткового множення до 8 разів 43.
Крок 2: Намалюйте риштування.
Крок 3: Сканування 3512, починаючи з крайньої лівої цифри, поки не отримаєте число більше або рівне 43. Спробуйте 3, потім 35, потім 351. Зверніть увагу, скільки ще цифр після 351. У цьому випадку є тільки один (2). Це означає, що ви можете взяти кратний десять разів 43 за один раз. (У старому стандартному алгоритмі, коли ви вгадаєте і ставите число вище 1 в 3512, ви ставите його в десятках місце значення.) Таким чином, ми ставимо нуль під зайвими числами в дивіденді (2) і стільки ж нулів праворуч від риштування. Залиште пробіл для цифри перед 0 праворуч від риштування.
Крок 4: Тепер подивіться на таблицю часткового множення, щоб визначити найбільше число, яке ви можете відняти від 351. Це 344, що в 8 разів 43. Зверніть увагу, що якщо 8 разів 43 дорівнює 344, то 80 разів 43 - 3440. Ви вже поставили додатковий нуль під 2, так що просто покласти 344 перед 0, що ви вже покласти вниз в кроці 3. Зверніть увагу, що 3440 це 80 разів 43, і вам потрібно стежити за тим, що праворуч від риштування. Ви вже написали нуль вниз на кроці 3, так що просто покласти 8 перед цим 0. Ви щойно віднімали вісімдесят 43 з дивідендів, оскільки 80 разів 43 3440. Відніміть 3440 з 3512, щоб отримати 72.
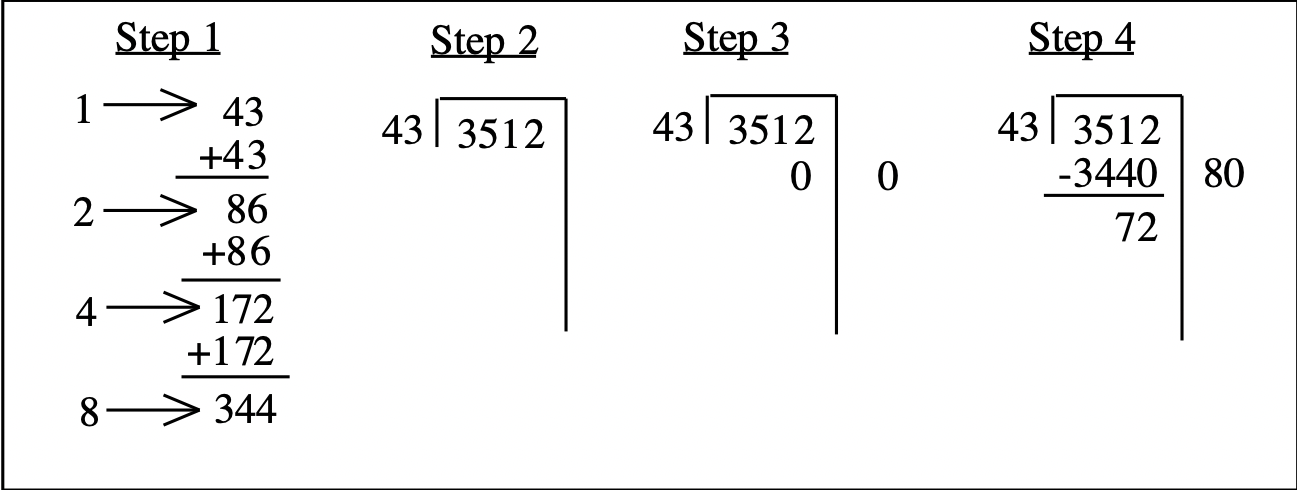
Крок 5: Тепер ми повинні побачити, скільки ще 43 можна відняти від 72. На цей час немає зайвих нулів, як у кроці 4. Ми можемо відняти ще 1 43 з 72, так що напишіть 1 праворуч від лісу, і відніміть 43 з 72, щоб отримати 29.
Кроки 6, 7 і 8: Оскільки 29 менше 43, тобто залишок, тому складіть цифри праворуч від риштування, щоб отримати частку. Напишіть відповідь як частка і залишок у вікні у верхній частині проблеми. Перевірте відповідь. За допомогою калькулятора можна помножити 81 на 43, що дорівнює 3483, а потім додати 29.
Останні чотири кроки наведені нижче.
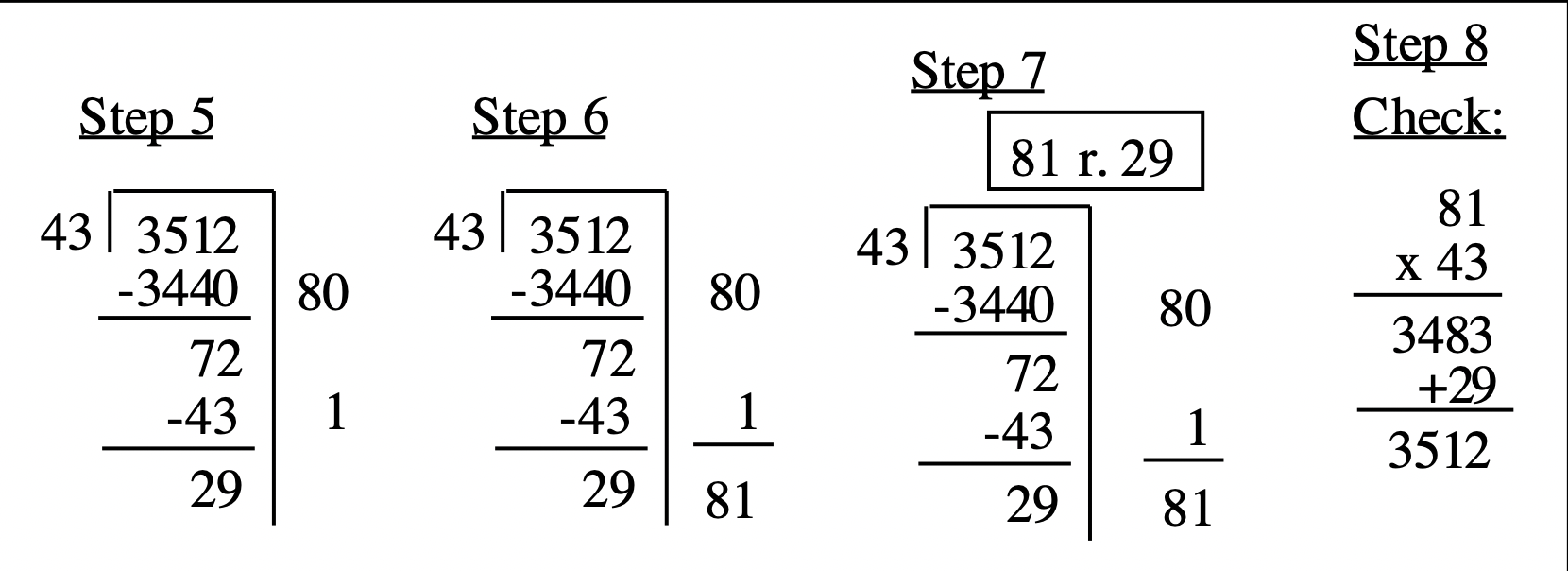
Якби ви показали свою роботу, ось як виглядала б вся проблема:
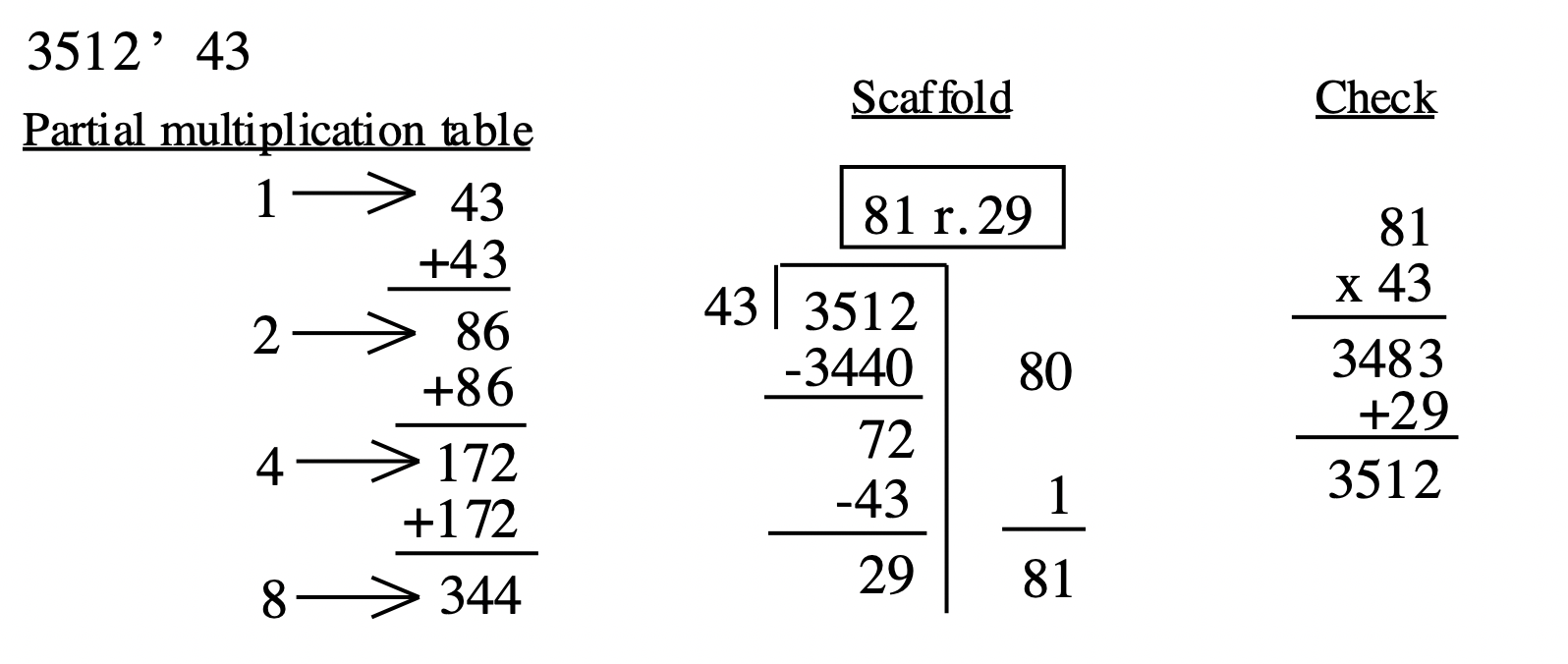
Ось як це виглядало б робити так, як ви це зробили у вправі 2:
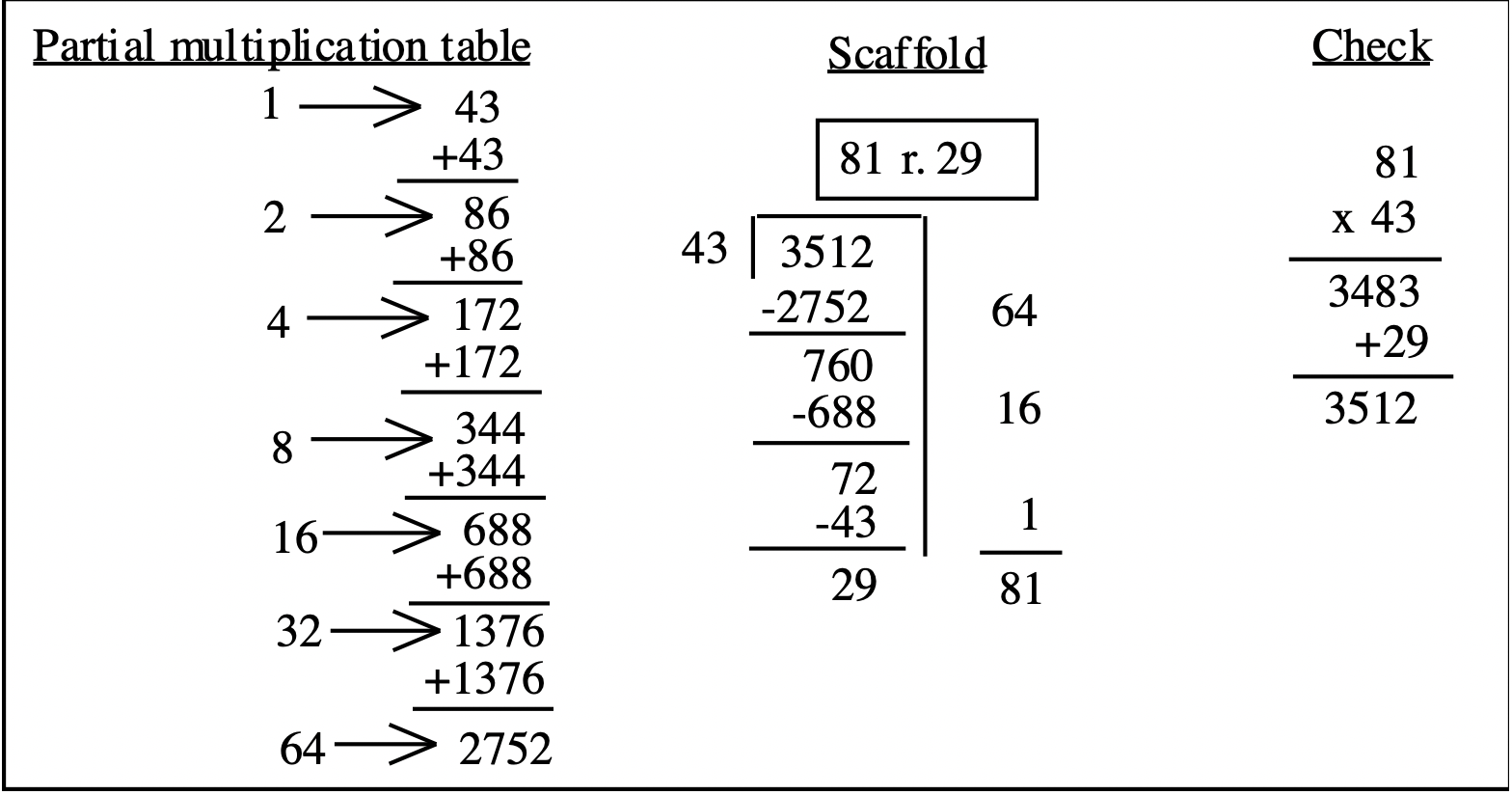
Для обох методів, коли ви додаєте числа праворуч від риштування, щоб отримати частку, будьте обережні, щоб вирівняти значення місця! Обидва способи дають однаковий результат і працюють однаково добре. Важливим є те, що процедура має сенс для вас!
Ще два приклади використання кратних десяткам (введення зайвих нулів) наведено нижче.
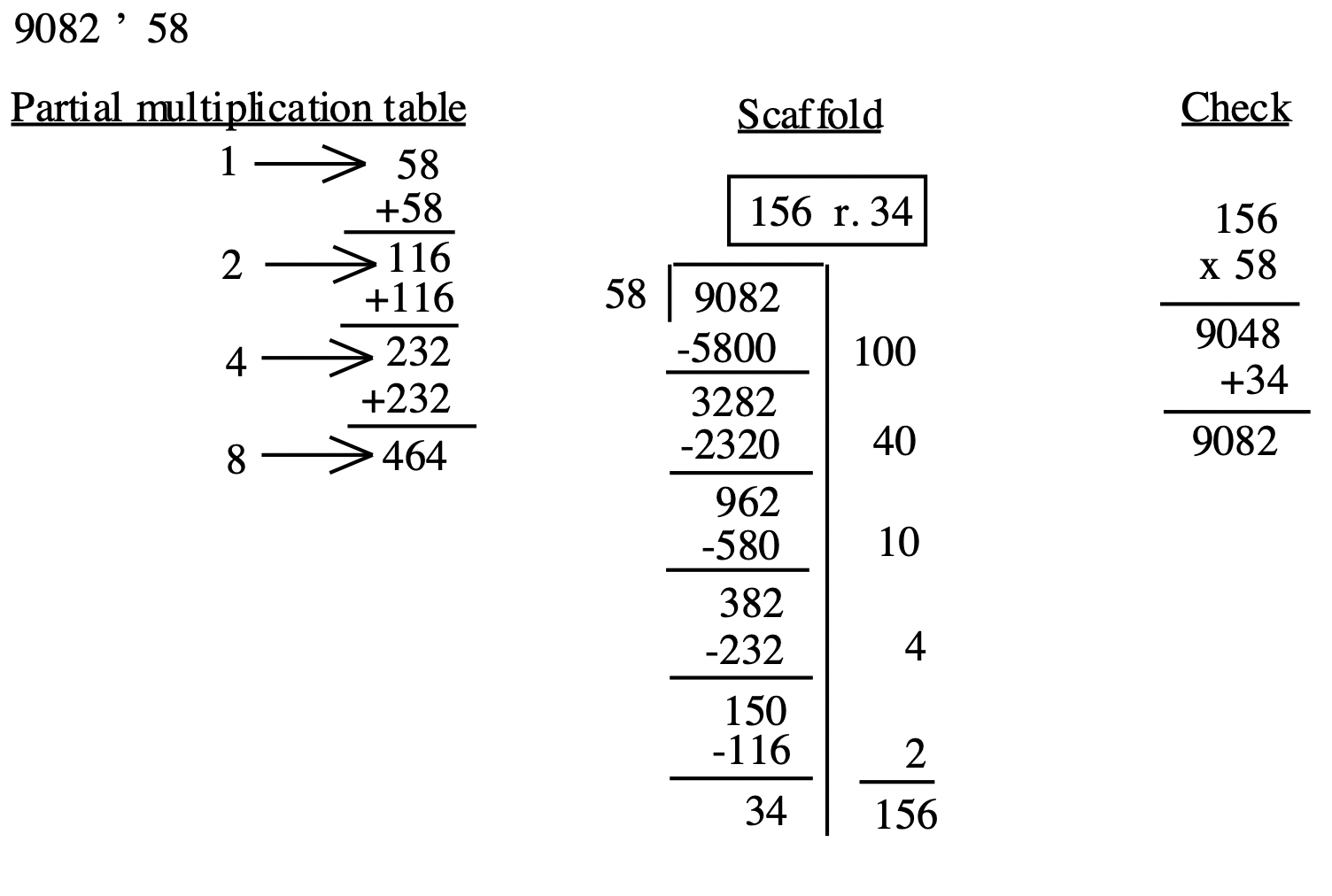
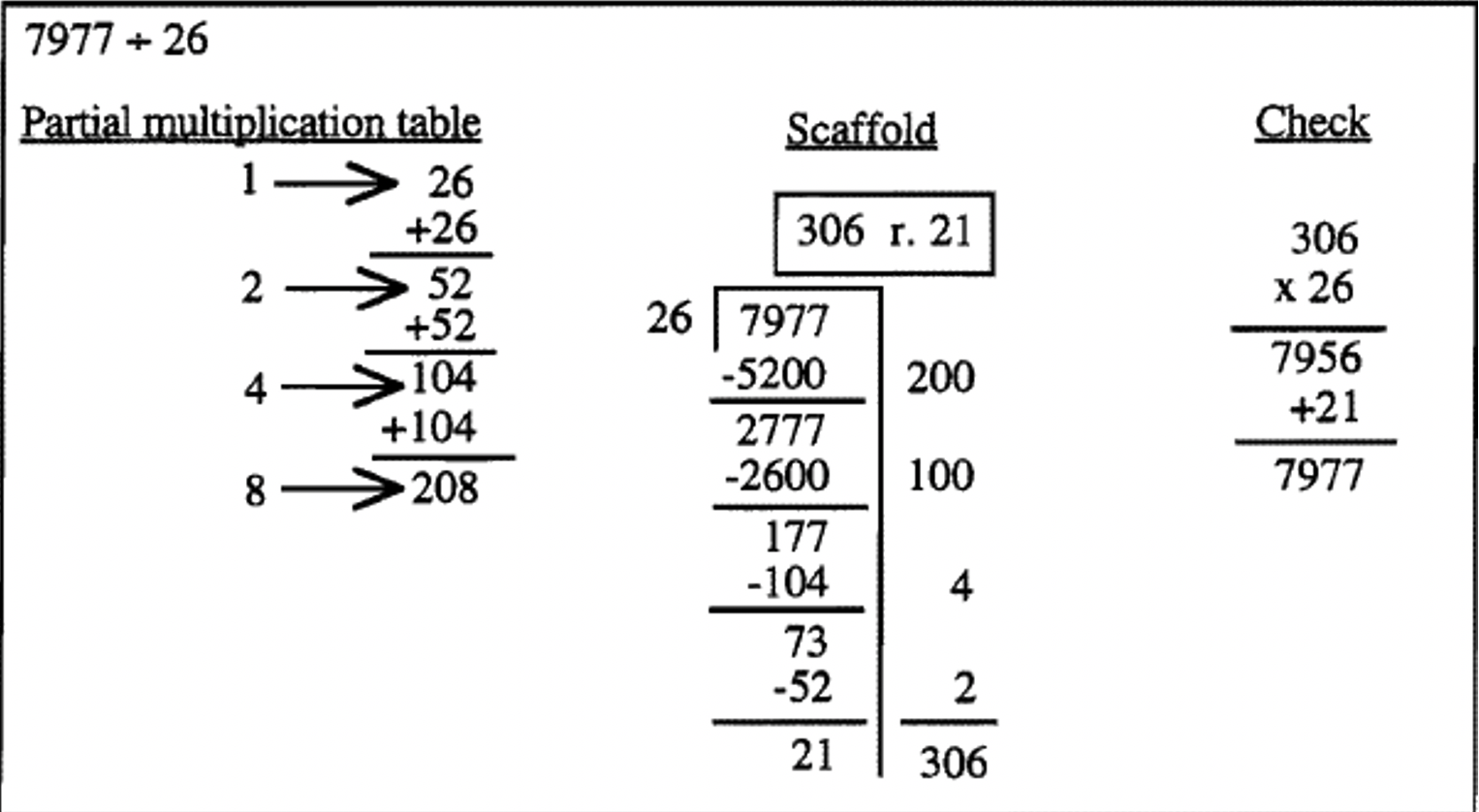
У наведеному вище прикладі багато людей (діти та дорослі) пропускають написання нульового місця в десятках для відповіді 306, коли вони роблять це коротким діленням, яким зазвичай навчають. Дуже поширеним відповіддю на цю проблему є 36 р. 21. На першому кроці вище, написання повного числа на стороні дійсно підкреслює той факт, що ви не просто множите 26 на 2, щоб отримати 52 ви множите 26 на 200, щоб отримати 5200. Ви знаєте, відповідь на проблему буде більше 200, так як ви вже віднімали 200 26 з 7977. Коли у вас залишилося 177, ви просто зауважте, що ви можете відняти лише кілька ще 26. Якщо хтось акуратно запише цифри праворуч, у десятках немає чисел, щоб скласти. Плутанина про нуль навіть не приходить!
Для кожної задачі ділення складіть таблицю часткового множення до 8 разів більше дільника. Потім намалюйте риштування та використовуйте повторне віднімання, щоб зробити кожне поділ. Використовуйте кратні десяткам (ставлячи зайві нулі там, де це необхідно) для виконання цих завдань. Потім перевірте відповідь. Всі роботи повинні бути показані в передбаченому просторі. Після перевірки напишіть відповідь на простір, надане на початку завдання. Калькулятор може бути використаний для перевірки відповіді, але запишіть кроки.
|
а.\(1230 \div 27\) = ______________
|
|||
|
б.\(603 \div 48\) = _______________
|
|||
|
с.\(1346 \div 41\) = ______________
|
|||
|
д.\(3512 \div 43\) = ______________
|
|||
|
е.\(66289 \div 325\) = ____________
|
|||
|
ф.\(5222 \div 21\) = ______________
|
Робити таблицю часткового множення на стороні, спільно з повторним методом віднімання, абсолютно необов'язково. Але, якщо ви складаєте таблицю першим, вам не потрібно робити ніякого множення або оцінки в голові. Інший варіант полягає в тому, щоб пропустити виконання таблиці часткового множення взагалі і все ще використовувати повторний метод віднімання. У цьому випадку, якщо ви не впевнені, скільки разів дільник можна відняти, недооцінюйте на кожному кроці, що ви не абсолютно впевнені, скільки дільника відняти. Іншими словами, переконайтеся, що ви не множите щось на дільник і вийшли з числом занадто великим, щоб відняти від дивідендів. Недооцінка - це нормально з повторним методом віднімання, тому що ви просто віднімаєте трохи більше на наступному кроці. Наприклад, у попередньому прикладі ви могли б відняти 200 26 (5200) на першому кроці, а потім ще 100 26 на другому кроці, або ви могли б відняти 300 26 на першому кроці, множивши 26 на 3 у вашій голові, якщо ви були впевнені, що 26 разів 3 не надто великий. Мені подобається таблиця часткового множення, тому що вона бере здогадки з проблеми. У наведеному нижче прикладі поділ виконується за допомогою повторного віднімання без складання таблиці. Замість цього ви оцінюєте, скільки дільника можна відняти на кожному кроці. При цьому множення потрібно робити в голові, або збоку, у міру проходження.
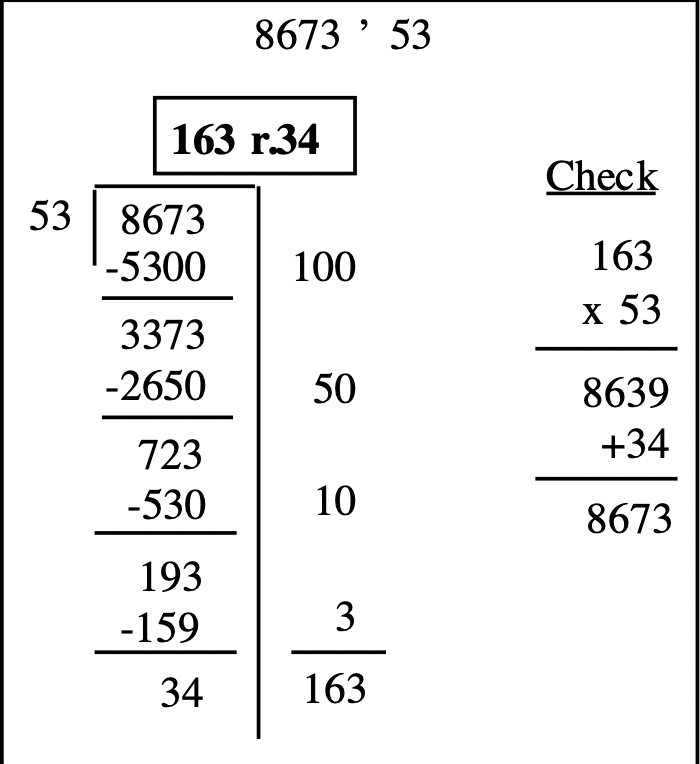
Ось спосіб розділити\(8673 \div 53\) без звичайної підготовчої роботи складання таблиці часткового множення в першу чергу. Це означає, що множення потрібно робити по шляху. Важливо зазначити, що це нормально недооцінювати при використанні повторного методу віднімання (на відміну від традиційного методу ділення), тому що ви завжди можете відняти більше на наступному кроці. З іншого боку, завищення призведе до того, що ви повернетеся назад і повторіть проблему. Спочатку зазначу, що 53 переходить в 86 один раз, тому я віднімаю 100 53, або 5300, від 8673. Далі оцінюємо\(337 \div 53\). Оскільки я не впевнений, що це 5 або 6 разів, я граю в безпеці і, отже, оцінюю 5. Отже, я віднімаю 50 разів 53, або 2650, від 3373. (Зверніть увагу, що я повинен зробити множення в голові.) Ну, я бачу ще 53 можна відняти від 72, тому я віднімаю 10 разів 53, або 530, від 723. Потім, я оцінюю 53 переходить в 193 принаймні 3 рази, тому я віднімаю 3 рази 53 з 193. Оскільки 34 менше 53, 34 - це залишок. Додайте числа збоку, щоб отримати частку 163. Перевірте, множивши\(53 \times 163\) і додавши залишок 34, щоб отримати 8673.
У традиційному алгоритмі поділу немає місця для недооцінки або завищення. Ви повинні повернутися назад і стерти, якщо ви поставили неправильну цифру в певному місці значення. Якщо ви неправильно оціните, множення, яке ви робите, закінчується марною тратою часу і сил, і вам доведеться починати спочатку. Крім того, більшість людей не думають про те, що або чому вони ставлять цифри в певному місці. Вони не думають про значення місця, або що поділ насправді стосується повторного віднімання. Я думаю, що метод ешафот, зі складанням таблиці часткового множення або без нього, сприяє кращому розумінню поділу і менш напружений, ніж традиційний метод «вгадати», де абсолютно немає місця для помилок. Однією з переваг традиційного алгоритму є те, що він є ярликом до методу риштування, і він використовує менше місця на папері.
Зрештою, це дійсно залежить від людини, яка робить поділ, щоб вирішити, яким способом це зробити.
Ось приклад ділення\(27984 \div 37\) за допомогою методу подвоєння.
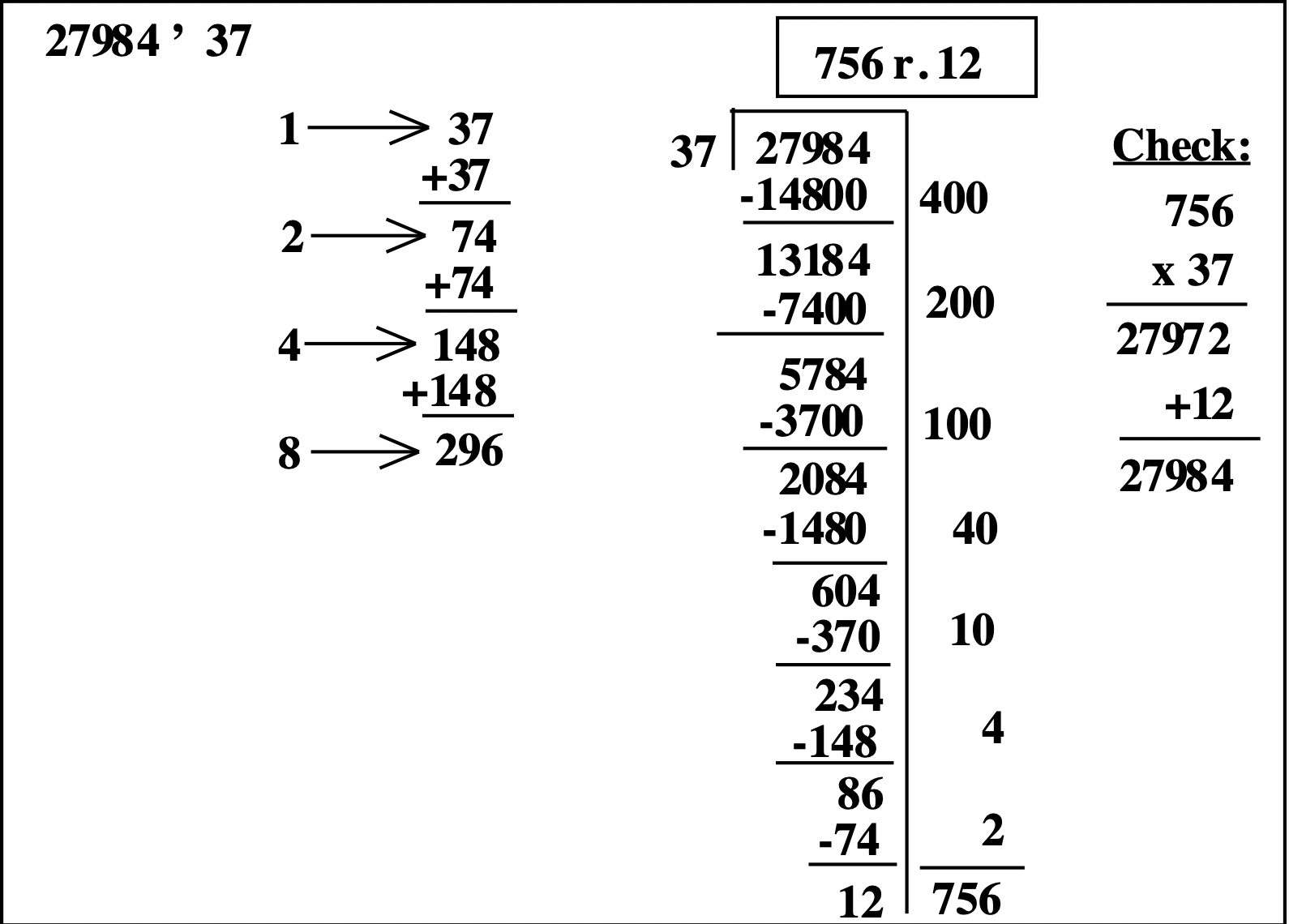
При складанні таблиці множення вона не повинна бути частковою. У базовій десятці подвоєння, щоб отримати дільник разів 1, 2, 4 або 8 дає нам досить близькі оцінки більшу частину часу. Найгірший можливий випадок полягає в тому, що 7 - це правильна кількість разів, коли щось можна відняти, як у наведеному вище прикладі. У такому випадку ми спочатку віднімаємо 4, потім 2, потім 1. Це трапляється не надто часто, але час від часу це відбувається. Інша стратегія полягає в тому, щоб додати ще одне доповнення до часткової таблиці, щоб ви також знали, що 6 разів дільник. Для цього, розібравшись, що в 4 рази дільник, додайте ще 2, як показано нижче (додайте 74 замість подвоєння 148), потім додайте ще 2 (знову додайте 74), щоб отримати 8 разів більше числа. Подивіться на різницю.
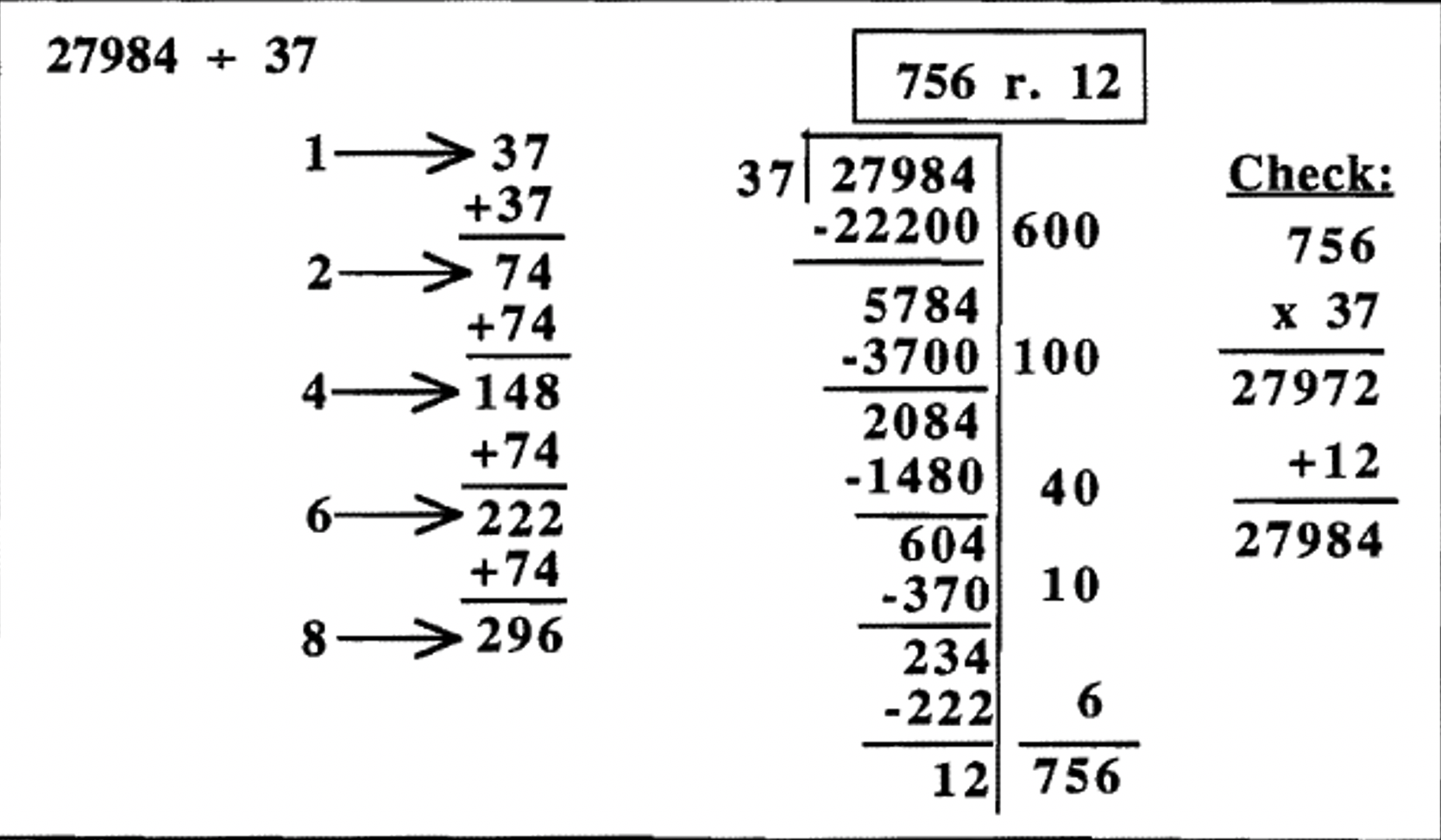
Насправді ми могли б використовувати повторне додавання, щоб дізнатися відповіді на дільник, який множиться на кожну цифру від 1 до 9, і в цьому випадку ніколи не відбудеться ні заниження, ні завищення. Хоча це зовсім не залишає жодних здогадок, це більше роботи, ніж потрібно в більшості випадків. Ось приклад того, як хтось може зробити ту саму проблему, що і на попередній сторінці, зробивши спочатку повну таблицю множення. Це легко зробити поділ, якщо ви робите це спочатку, але є багато підготовчої роботи на початку, щоб зробити стіл.
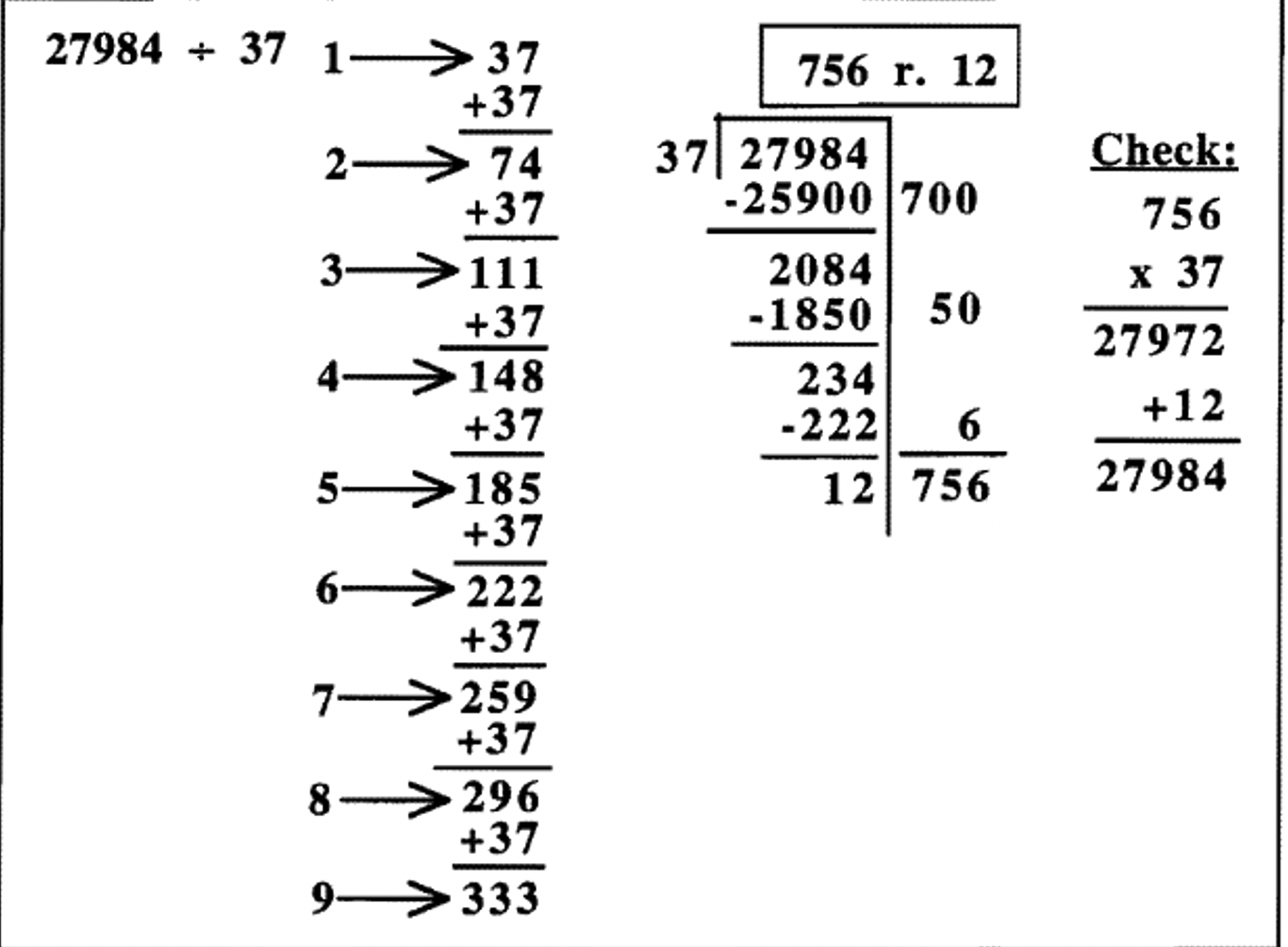
Озирніться назад на три різні способи поділу\(27984 \div 37\). Перший спосіб, показаний на попередній сторінці, мав коротку таблицю часткового множення (всього три додавання для підготовчої роботи), але повторний метод віднімання зайняв трохи більше часу. Потрібно було сім віднімань, щоб отримати відповідь (подивіться праворуч від риштування), тому що 700 зробили три кроки 400, 200, 100; 50 зробили два кроки 40 і 10; а 6 зробив два кроки 4 і 6. Другий спосіб мав ще одне додавання для підготовки таблиці множення, а потім вимагав лише п'ять віднімань, щоб отримати відповідь (подивіться праворуч від риштування), тому що 700 взяв два кроки 600 і 100; 50 зробив два кроки 40 і 10; і 6 зробив один крок. Третій спосіб, показаний вгорі, вимагав восьми доповнень підготовчої роботи, щоб скласти таблицю множення, але ділення було легким вітерцем, зробивши всього три кроки. Якщо ви робите це таким чином, ви можете також написати 756 вгорі, як ви робите це за допомогою традиційного алгоритму, тому що ви ніколи не можете недооцінювати або переоцінити.
Залежно від конкретної проблеми, один метод може бути швидшим, ніж інший, але багато разів ви не знаєте, поки не завершите проблему. Я зазвичай просто роблю подвоєння до 8, щоб отримати досить хороші оцінки, але якщо ви хочете зробити більш повну таблицю, вона працює так само добре. Ви повинні вирішити, якщо ви віддаєте перевагу робити більше підготовчої роботи вперед, щоб, можливо, зробити поділ швидше.
