7.1: Значення поділу
- Page ID
- 66954
Вам знадобляться: сантиметрові смужки (матеріальні картки 16A-16L) та базові блоки (матеріальні картки 3 - 15)
У цих перших кількох вправах ви будете використовувати c-смужки для вивчення поділу.
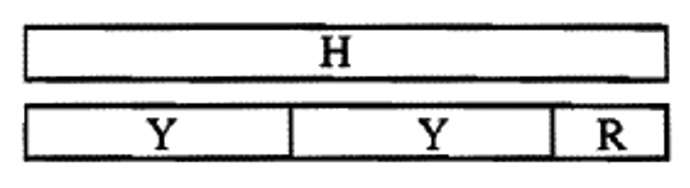
У цій першій вправі ми розділимо\(H \div Y\). H, частина перед знаком поділу, називається ДИВІДЕНДОМ, а Y, частина після знака поділу, називається ДІЛЬНИКОМ. Один із способів зробити це поділ - знайти максимальну кількість разів, коли дільник (Y) можна відняти від дивіденду (H). Вийміть яскраво-рожеву c-смужку (H). Щоб з'ясувати, скільки жовтих c-смужок можна було б відняти, складіть поїзд, що складається з якомога більшої кількості жовтих c-смужок (Y) таким чином, щоб поїзд, який ви робите, був коротшим або рівним довжині H, і якби ви додали ще одну жовту c-смужку, поїзд був би довшим, ніж гаряча рожева c-смужка.
а. скільки жовтих c-смужок ви використовували? ______
Це число називається КОЕФІЦІЄНТОМ.
Коефіцієнт - це максимальна кількість разів, коли дільник можна відняти від дивіденду.
б Якщо поїзд, який ви зробили, коротший за H, який колір c-смуги
ви могли б додати до цього поїзда, щоб зробити його рівним по довжині яскраво-рожевій c-смузі? ______
Цей шматок, який повинен бути коротше дільника, називається REAMENDER.
Покладіть яскраво-рожеву смужку поруч зі сформованим шлейфом. Виглядати він повинен наступним чином:
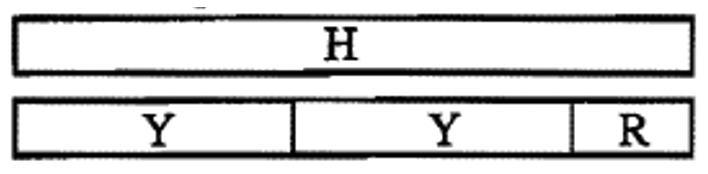
Для обчислення нам потрібно розібратися\(H \div Y\), що йде в пробілах, щоб рівняння в частині c, нижче, вірним. Перший бланк повинен містити найбільшу можливу c-смужку, яка зробить рівняння істинним, а другий бланк повинен бути коротшим, ніж жовта c-смужка. Ми зробили поїзд жовтих, щонайменше один додатковий шматок, щоб сформувати довжину H. Зверніть увагу, що це поїзд жовтих (які можуть бути сформовані в прямокутник) плюс додатковий шматок. Сформуйте дві жовті смужки в прямокутник і знайдіть c-смужку, яка йде по ширині. Ця c-смужка йде в першу заготовку, а зайвий шматок (R) йде у другій заготовці. Заповніть пропуски рівняння нижче. Це рівняння має сенс, дивлячись на картинку вище, що показує Н і поїзд однакової довжини.
с.Н = ____\(\cdots Y\) + ____
Коефіцієнт виділений жирним шрифтом, а ЗАЛИШОК підкреслено.
Тепер ми можемо зробити висновок, що:\(H \div Y\) =\(\mathbf{R}\) залишок\(\underline{R}\), так як\(H = \mathbf{R} \cdots Y\) +\(\underline{R}\)
Це можна записати як твердження про числа, переводячи кожну c-смужку в число.
Використовуючи числа у вищевказаному рівнянні,\(12 \div 5\) =\(\mathbf{2}\) залишок\(\underline{2}\), оскільки 12 =\(\mathbf{2} \cdots 5\) +\(\underline{2}\)
Для a - e, зробіть поділ за допомогою c-смуг, щоб зробити поїзд якомога більше дільника таким чином, щоб довжина поїзда, який ви робите, була меншою або дорівнює довжині дивіденду, і якщо ви повинні були додати ще один дільник до поїзда, він був би довшим, ніж дивіденд. Якщо поїзд закінчиться такою ж довжиною, як і дивіденд, залишку не буде, а другий порожній буде порожнім. Намалюйте діаграму, що показує c-смужку, яка є дивідендом, і під нею намалюйте сформований вами поїзд. Робіть це так само, як ми це робили для вправи 1. Дотримуйтесь наведеного нижче прикладу.
\(H \div Y\)=\(\mathbf{R}\) залишок\(\underline{R}\), так як H =\(\mathbf{R}\)\(\cdots\) Y +\(\underline{R}\)
\(12 \div 5\)=\(\mathbf{2}\) залишок\(\underline{2}\), так як 12 =\(\mathbf{2}\)\(\cdots\) 5 +\(\underline{2}\)
Показати діаграму нижче:
|
а.\(B \div R:\) \( B \div R\)= __ залишок __ так як B = __\(\cdots\) R + __ __\(\div\) __ = __ залишок __ з __ = __\(\cdots\) __ + __ Показати діаграму нижче: |
|
б. S\(\div\) Л: S\(\div\) L = __ залишок __ так як S = __\(\cdots\) L + __ __\(\div\) __ = __ залишок __ з __ = __\(\cdots\) __ + __ Показати діаграму нижче: |
|
c.\(N \div P:\) \( N \div P\)= __ залишок __ так як N = __\(\cdots\) P + __ __\(\div\) __ = __ залишок __ з __ = __\(\cdots\) __ + __ Показати діаграму нижче: |
|
д.\(K \div P:\) \( K \div P\)= __ залишок __ так як K = __\(\cdots\) P + __ __\(\div\) __ = __ залишок __ з __ = __\(\cdots\) __ + __ Показати діаграму нижче: |
|
е.\(D \div L:\) \( D \div L\)= __ залишок __ так як D = __\(\cdots\) L + __ __\(\div\) __ = __ залишок __ з __ = __\(\cdots\) __ + __ Показати діаграму нижче: |
Підрахуйте 36 одиничних блоків. Як би ви розділили 36 блоків на 2? Поясніть, як би ви це зробили, і покажіть картину того, що ви зробили. Яка відповідь?
Отримайте свою базу чотири блоки зараз, і торгуйте 36 одиницями для числа в базовій четвертій.
а. напишіть 36 як основу чотири числівники: _____________
Вирішіть, як розділити це на 2, використовуючи базові чотири блоки.
б Поясніть, як би ви це зробили, і покажіть картину того, що ви зробили.
c Яка відповідь у базовій четвірці? _________
d Запишіть задачу поділу і частку (відповідь) в основі чотири: ____________\( \div 2_{\text{four}}\) = ____________
Вийдіть з вашої бази три блоки зараз, і торгуйте в 36 одиниць за число в базі три.
а. напишіть 36 в якості основи три числівники: _____________
Вирішіть, як розділити це на 2 за допомогою основи три блоки.
б Поясніть, як би ви це зробили, і покажіть картину того, що ви зробили.
c Яка відповідь у третій базі? _________
d Запишіть задачу поділу і частку (відповідь) в основі три: ____________\( \div 2_{\text{three}}\) = ____________
Підрахуйте 36 одиничних блоків. Як би ви розділили 36 блоків на 3? Поясніть, як би ви це зробили, і покажіть картину того, що ви зробили. Яка відповідь?
Отримайте свою базу чотири блоки зараз, і торгуйте 36 одиницями для числа в базовій четвертій.
а. напишіть 36 як основу чотири числівники: _____________
Вирішіть, як розділити це на 3, використовуючи базові чотири блоки.
б Поясніть, як би ви це зробили, і покажіть картину того, що ви зробили.
c Яка відповідь у базовій четвірці? _________
d Запишіть задачу поділу і частку (відповідь) в основі чотири: ____________\( \div 3_{\text{four}}\) = ____________
Підрахуйте 48 одиничних блоків. Як би ви розділили 48 блоків на 16? Поясніть, як би ви це зробили, і покажіть картину того, що ви зробили. Яка відповідь?
Існує два основних способи мислення про поділ. Дві проблеми слів нижче вимагають поділу\(18 \div 3\), але проблеми насправді зовсім різні.
Якщо у вас є 18 файлів cookie і ви хочете розділити печиво порівну між вашими трьома дітьми, скільки печива ви повинні дати кожній дитині?
Якщо у вас є 18 печива і ви хочете зробити мішки, що мають три печива в кожному, щоб покласти в ланч-бокси, скільки мішків ви зможете зробити?
Обидва вимагають задачі поділу\(18 \div 3\), і відповідь на кожну проблему - 6. Але картина, яка використовується для вирішення кожного, дуже різна.
У Word Problem A вам розповідають, скільки дітей, і вас просять з'ясувати, скільки печива потрібно дати кожній дитині. Уявіть перед собою 3 дітей. Вам потрібно розподілити файли cookie серед дітей 3, щоб кожен отримував однакову кількість файлів cookie. Для початку ви можете намалювати модель для представлення трьох дітей. Це може виглядати приблизно так:

Ви знаєте, що є 3 дітей, і кожному буде надано однакову кількість печива, так що загальна кількість печива вони всі мають 18. Після виплати ви можете показати картинку так:

Це спосіб проілюструвати, що кожен з 3 дітей має 6 печиво. Якщо ви віддаєте перевагу, ви можете насправді намалювати 6 крапок або 6 печива в кожному колі. Це вирішувати вам.
Зверніть увагу, що якщо ви подивитеся на намальовану модель, це просто проблема множення 3\(\cdots\) 6, оскільки є 3 набори по 6, складені разом. Тлумачення поділу Word Задача А представляє називається:
Розбиття на (рівні) підмножини
У цій інтерпретації дільник - це кількість підмножин, в яких потрібно щось розплачувати. Дивіденд, 18, повинен бути розділений на 3 рівні підмножини (3 - дільник). Частним (відповіддю на задачу ділення) буде кількість елементів (6), розміщених у кожній підмножині (у цьому випадку діти). Завдання полягає в тому, щоб розділити 18 файлів cookie на 3 рівні підмножини. У цій інтерпретації вам дається, скільки підмножин (з прочитання проблеми в даному випадку кожен малюк представляє одну підмножину), але ви не знаєте, скільки в кожній підмножині (саме таке питання задається в даному випадку, скільки файлів cookie повинна отримати кожна дитина). Ви робите поділ, щоб з'ясувати, скільки елементів буде в кінцевому підсумку в кожній підмножині. Після виконання ділення кількість елементів В кожній підмножині є відповіддю на задачу.
Один із способів відрізнити, що проблема передбачає цю інтерпретацію, полягає в тому, щоб розглянути, чи надає інформація в проблемі кількість підмножин. Якщо це так, як у Word Problem A, то це розбиття на рівні підмножини інтерпретації.
Гаразд, давайте зараз подивимося на проблему Word B.
Якщо у вас є 18 печива і ви хочете зробити мішки, що мають три печива в кожному, щоб пізніше покласти в ланч-бокси, скільки мішків ви зможете зробити?
У Word Problem B ви не знаєте, скільки підмножин буде. Насправді, вас запитують, скільки підмножин ви зможете зробити, тому розбиття на підмножини інтерпретація не застосовуватиметься.
Те, що ви знаєте, скільки щось буде в кожному підмножині. Ви б помістити три печива в мішечок, потім ще 3 в інший мішок, і так далі. Ви не будете знати, скільки підмножин у вас буде, поки не закінчите виплачувати файли cookie. Ви б забирали три печива одночасно і клали їх у мішечок, поки у вас не закінчилося печиво. Після цього зображення, яке ви можете намалювати для ілюстрації цієї процедури, може виглядати наступним чином:

Знову ж таки, якщо ви віддаєте перевагу показувати три точки в кожному колі, на відміну від того, щоб просто писати цифру 3, в кожному колі, це прекрасно. Так чи інакше, з малюнка повинно бути зрозуміло, яка процедура була використана.
Після виплати всіх печива, ви б порахували, скільки мішків ви змогли зробити, і це дасть вам відповідь. Зверніть увагу на відповідь 6, в даному випадку. Наведена модель являє собою множення\(6 \cdots 3\), оскільки є 6 мішків по 3 печива в кожному.
Тлумачення поділу Word Задача B представляє називається:
Повторне віднімання
У цій інтерпретації дільник - це кількість елементів, які будуть йти в кожну підмножину. Кожен раз, коли дільник (3) віднімається з дивіденду (18), формується підмножина. Після того, як всі елементи були виплачені, частка (відповідь) знаходять, підрахувавши, скільки підмножин було сформовано. Ця інтерпретація використовується, коли вам задано, скільки елементів у кожній підмножині, і ви намагаєтеся з'ясувати, скільки підмножин можна зробити (це питання, яке задається). Ви робите поділ (за допомогою повторного віднімання), щоб з'ясувати, скільки підмножин можна зробити. Після виконання ділення кількість підмножин, які ви зробили, є відповіддю на проблему.
Один із способів відрізнити, що проблема передбачає цю інтерпретацію, полягає в тому, щоб розглянути, чи надає інформація в проблемі, скільки елементів переходять у підмножину. Якщо так, як у Word Problem B, то це багаторазова інтерпретація віднімання.
Проблеми слів, що вимагають поділу, зазвичай потрапляють до категорії повторного віднімання або розбиття на підмножини. Прочитавши проблему слова, ви повинні мати можливість проаналізувати та інтерпретувати її як проблему, яка вимагає розділення на підмножини або повторне віднімання для вирішення проблеми, а потім мати можливість намалювати малюнок, використовуючи цю інтерпретацію. Крім того, для будь-якої задачі поділу, ви повинні мати можливість написати дві різні проблеми слів, по одній для кожного тлумачення, і намалювати картину для кожного тлумачення, а також бути в змозі пояснити і показати всі кроки, необхідні для вирішення проблеми.
Террі хотів розділити 100 кульок серед своїх трьох кращих друзів і себе. Скільки мармуру кожен з них отримає?
- Яку проблему поділу потрібно зробити, щоб знайти відповідь?
- Яке тлумачення поділу представляє це слово проблема?
- Поясніть, як використовувати правильне тлумачення, щоб намалювати картину, щоб знайти відповідь.
- Намалюйте картинку, використовуючи правильне тлумачення, щоб допомогти знайти відповідь.
- Напишіть задачу множення, показану на малюнку:
- Поясніть, як ви використовуєте картинку, щоб знайти відповідь на проблему. Будьте конкретні.
- Яка відповідь на цю проблему? ______
Йорданія зробила 80 унцій желе, і хотіла помістити їх у 8 унцій контейнерів. Скільки ємностей вона може заповнити?
- Яку проблему поділу потрібно зробити, щоб знайти відповідь?
- Яке тлумачення поділу представляє це слово проблема?
- Поясніть, як використовувати правильне тлумачення, щоб намалювати картину, щоб знайти відповідь.
- Намалюйте картинку, використовуючи правильне тлумачення, щоб допомогти знайти відповідь.
- Напишіть задачу множення, показану на малюнку:
- Поясніть, як ви використовуєте картинку, щоб знайти відповідь на проблему. Будьте конкретні.
- Яка відповідь на цю проблему? ______
Енджі мала 144 сторінки чистого паперу. Вона робила копії 16-сторінкового короткого оповідання, яке вона написала, щоб відправити в журнали. Скільки повних копій вона могла зробити?
- Яку проблему поділу потрібно зробити, щоб знайти відповідь?
- Яке тлумачення поділу представляє це слово проблема?
- Поясніть, як використовувати правильне тлумачення, щоб намалювати картину, щоб знайти відповідь.
- Намалюйте картинку, використовуючи правильне тлумачення, щоб допомогти знайти відповідь.
- Напишіть задачу множення, показану на малюнку:
- Поясніть, як ви використовуєте картинку, щоб знайти відповідь на проблему. Будьте конкретні.
- Яка відповідь на цю проблему? ______
Група з чотирьох друзів об'єднала свої гроші разом для деяких лотерейних квитків і виграла 500 доларів. Скільки отримує кожна людина від виграшу?
- Яку проблему поділу потрібно зробити, щоб знайти відповідь?
- Яке тлумачення поділу представляє це слово проблема?
- Поясніть, як використовувати правильне тлумачення, щоб намалювати картину, щоб знайти відповідь.
- Намалюйте картинку, використовуючи правильне тлумачення, щоб допомогти знайти відповідь.
Шейла хотіла зробити якомога більше коржів з рецепта, що вимагає 1\(\frac{1}{3}\) склянки борошна на кожен корж. У неї було 8 склянок борошна. Скільки тортів вона могла зробити?
- Яку проблему поділу потрібно зробити, щоб знайти відповідь?
- Яке тлумачення поділу представляє це слово проблема?
- Поясніть, як використовувати правильне тлумачення, щоб намалювати картину, щоб знайти відповідь.
- Намалюйте картинку, використовуючи правильне тлумачення, щоб допомогти знайти відповідь.
- Напишіть задачу множення, показану на малюнку:
- Поясніть, як ви використовуєте картинку, щоб знайти відповідь на проблему. Будьте конкретні.
- Яка відповідь на цю проблему? ______
Том виграв 65 бейсбол і вирішив розділити їх рівномірно серед 13 хлопчиків на своїй бейсбольній команді. Скільки бейсболів отримає кожен малюк?
- Яку проблему поділу потрібно зробити, щоб знайти відповідь?
- Яке тлумачення поділу представляє це слово проблема?
- Поясніть, як використовувати правильне тлумачення, щоб намалювати картину, щоб знайти відповідь.
- Намалюйте картинку, використовуючи правильне тлумачення, щоб допомогти знайти відповідь.
- Напишіть задачу множення, показану на малюнку:
- Поясніть, як ви використовуєте картинку, щоб знайти відповідь на проблему. Будьте конкретні.
- Яка відповідь на цю проблему? ______
Якщо вам не представлена проблема зі словом, а просто задається проблема поділу, ви можете використовувати будь-яку інтерпретацію, щоб подумати і вирішити проблему. Багато разів простіше використовувати одну інтерпретацію над іншою, особливо якщо вам потрібно намалювати картинку, щоб показати, як ви вирішили проблему.
Розглянемо наступну проблему поділу:\(26 \div 2\). Припустимо, 26 представляли 2 копійки. Було б простіше розділити 26 копійок на 2 палі і порахувати, скільки в кожній купі; або було б простіше зробити кілька рівних підмножин, що містять 2 копійки кожна з 26 копійок, а потім підрахувати, скільки підмножин є? Картинка, яку ви малюєте для представлення кожної інтерпретації, зовсім інша. Подивіться на різницю:
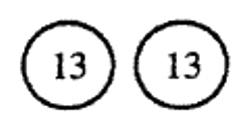
Показано зображення, яке використовує інтерпретацію Розбиття на підмножини:
Зображення, що використовує інтерпретацію повторного віднімання, показано нижче:
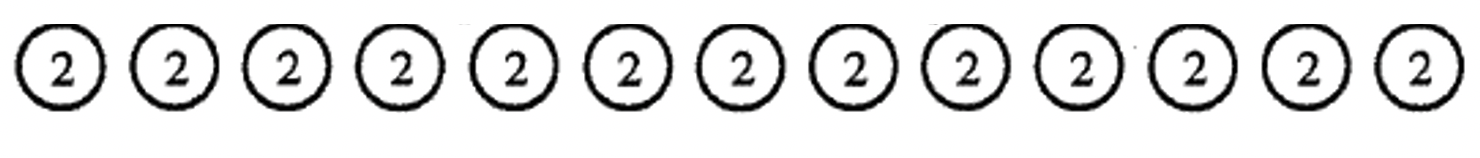
Для частин а - ч цієї вправи розглянемо задачу поділу:\(\bf 48 \div 12\).
- Яке тлумачення, на вашу думку, було б легше використовувати, якщо вам потрібно було намалювати картину?
- Поясніть, чому інтерпретація, яку ви вибрали частково а, було б легше використовувати.
- Складіть слово завдання, що вимагає поділу\(48 \div 12\), таким чином, щоб було використано розбиття на підмножини інтерпретації. Переконайтеся, що ваша проблема задає питання!
- Намалюйте малюнок, щоб вирішити вашу проблему за допомогою інтерпретації Розбиття на підмножини:
- Множення для малюнка, показаного в частині d, становить: ____________________
- Складіть слово завдання, що вимагає поділу\(48 \div 12\), таким чином, щоб використовується повторне тлумачення віднімання. Переконайтеся, що ваша проблема задає питання!
- Намалюйте малюнок, щоб вирішити вашу проблему, використовуючи інтерпретацію повторного віднімання:
- Множення для малюнка, показаного в частині g, становить: ____________________
Для частин а - ч цієї вправи розглянемо задачу поділу:\(\bf 200 \div 4\).
- Яке тлумачення, на вашу думку, було б легше використовувати, якщо вам потрібно було намалювати картину?
- Поясніть, чому інтерпретація, яку ви вибрали частково а, було б легше вирішити цю проблему поділу. Контрастуйте його з іншою інтерпретацією.
- Складіть слово завдання, що вимагає поділу\(200 \div 4\), таким чином, щоб було використано розбиття на підмножини інтерпретації. Переконайтеся, що ваша проблема задає питання!
- Намалюйте малюнок, щоб вирішити вашу проблему за допомогою інтерпретації Розбиття на підмножини:
- Множення зображення за допомогою Розбиття на підмножини: ________
- Складіть слово завдання, що вимагає поділу\(200 \div 4\), таким чином, щоб використовується повторне тлумачення віднімання. Переконайтеся, що ваша проблема задає питання!
- Поясніть, що вам доведеться зробити, якби вам довелося намалювати малюнок, щоб вирішити вашу проблему, використовуючи інтерпретацію повторного віднімання. Насправді не малюйте картинку — просто поясніть.
- Множення для зображення за допомогою повторного віднімання буде таким:
Для частин а - ч цієї вправи розглянемо задачу поділу:\( 150 \div 50\).
- Яке тлумачення, на вашу думку, було б легше використовувати, якщо вам потрібно було намалювати картину?
- Поясніть, чому інтерпретація, яку ви вибрали частково а, було б легше вирішити цю проблему поділу. Контрастуйте його з іншою інтерпретацією.
- Складіть слово завдання, що вимагає поділу\(150 \div 50\), таким чином, щоб було використано розбиття на підмножини інтерпретації. Переконайтеся, що ваша проблема задає питання!
- Поясніть, що вам доведеться зробити, якби вам довелося намалювати малюнок, щоб вирішити вашу проблему за допомогою інтерпретації «Розділення на підмножини». Насправді не малюйте картинку — просто поясніть!
- Множення зображення за допомогою розділення на підмножини буде: ____
- Складіть слово завдання, що вимагає поділу\(150 \div 50\), таким чином, щоб використовується повторне тлумачення віднімання. Переконайтеся, що ваша проблема задає питання!
- Намалюйте малюнок, щоб вирішити вашу проблему, використовуючи інтерпретацію повторного віднімання:
- Множення для зображення за допомогою повторного віднімання: ___________
Для частин а - ч цієї вправи розглянемо задачу поділу:\(\bf 140 \div 35\).
- Яке тлумачення, на вашу думку, було б легше використовувати, якщо вам потрібно було намалювати картину?
- Поясніть, чому інтерпретація, яку ви вибрали частково а, було б легше вирішити цю проблему поділу. Контрастуйте його з іншою інтерпретацією.
- Складіть слово завдання, що вимагає поділу\(140 \div 35\), таким чином, щоб було використано розбиття на підмножини інтерпретації. Переконайтеся, що ваша проблема задає питання!
- Поясніть, що вам доведеться зробити, якби вам довелося намалювати малюнок, щоб вирішити вашу проблему за допомогою інтерпретації «Розділення на підмножини». Насправді не малюйте картинку — просто поясніть!
- Множення зображення за допомогою розділення на підмножини буде: ____
- Складіть слово завдання, що вимагає поділу\(140 \div 35\), таким чином, щоб використовується повторне тлумачення віднімання. Переконайтеся, що ваша проблема задає питання!
- Намалюйте малюнок, щоб вирішити вашу проблему, використовуючи інтерпретацію повторного віднімання:
- Множення зображення за допомогою повторного віднімання:
Для частин а - ч цієї вправи розглянемо задачу поділу:\(\bf 95 \div 5\).
- Яке тлумачення, на вашу думку, було б легше використовувати, якщо вам потрібно було намалювати картину?
- Поясніть, чому інтерпретація, яку ви вибрали частково а, було б легше вирішити цю проблему поділу. Контрастуйте його з іншою інтерпретацією.
- Складіть слово завдання, що вимагає поділу\(95 \div 5\), таким чином, щоб було використано розбиття на підмножини інтерпретації. Переконайтеся, що ваша проблема задає питання!
- Намалюйте малюнок, щоб вирішити вашу проблему за допомогою інтерпретації Розбиття на підмножини:
- Множення зображення за допомогою Розбиття на підмножини: ________
- Складіть слово завдання, що вимагає поділу\(95 \div 5\), таким чином, щоб використовується повторне тлумачення віднімання. Переконайтеся, що ваша проблема задає питання!
- Поясніть, що вам доведеться зробити, якби вам довелося намалювати малюнок, щоб вирішити вашу проблему, використовуючи інтерпретацію повторного віднімання. Насправді не малюйте картинку — просто поясніть!
- Множення для зображення за допомогою повторного віднімання буде: ______
Для частин а - ч цієї вправи розглянемо задачу поділу:\(\bf 800 \div 160\).
- Яке тлумачення, на вашу думку, було б легше використовувати, якщо вам потрібно було намалювати картину?
- Поясніть, чому інтерпретація, яку ви вибрали частково а, було б легше вирішити цю проблему поділу. Контрастуйте його з іншою інтерпретацією.
- Складіть слово завдання, що вимагає поділу\(800 \div 160\), таким чином, щоб було використано розбиття на підмножини інтерпретації. Переконайтеся, що ваша проблема задає питання!
- Поясніть, що вам доведеться зробити, якби вам довелося намалювати малюнок, щоб вирішити вашу проблему за допомогою інтерпретації «Розділення на підмножини». Насправді не малюйте картинку — просто поясніть!
- Множення зображення за допомогою розділення на підмножини буде: ____
- Складіть слово завдання, що вимагає поділу\(800 \div 160\), таким чином, щоб використовується повторне тлумачення віднімання. Переконайтеся, що ваша проблема задає питання!
- Намалюйте малюнок, щоб вирішити вашу проблему, використовуючи інтерпретацію повторного віднімання:
- Множення зображення за допомогою повторного віднімання:
Для кожної задачі поділу показана картинка. Спираючись на картину, станьте, яке тлумачення поділу було використано.
|
а. 84 + 21 Тлумачення: _______  |
|
б. 85 + 5 Тлумачення: _______  |
|
c. 30 + 5 Тлумачення: _______  |
|
д. 30 + 6 Тлумачення: _______  |
Для кожної картини використовувалася певна інтерпретація поділу для вирішення проблеми поділу. Виходячи з інтерпретації та картини, вирішіть, якою була початкова проблема поділу, і обведіть правильний один із двох наведених варіантів.
|
а. повторне віднімання  Обведіть правильну задачу поділу: 56 + 8 або 56 + 7 |
|
а. повторне віднімання  Обведіть правильну задачу поділу: 56 + 8 або 56 + 7 |
Для кожної картини використовувалася певна інтерпретація поділу для вирішення проблеми поділу. Виходячи з цієї інтерпретації та картини, викладіть оригінальну проблему поділу.
|
a. поділ на підмножини  Якщо було використано поділ на підмножини, вкажіть проблему поділу: ___________ |
|
b. повторне віднімання  Якщо було використано повторне віднімання, вкажіть задачу ділення: ___________ |
Якщо ви намалювали картинку для задачі множення, a\(\cdots\) b, яка буква представляє, як створюються підмножини, а яка буква представляє, скільки в кожній підмножині?
Розподіл - це операція, яка скасовує калібрування. Студенти можуть покластися на цей факт, щоб дізнатися основні факти поділу. Наприклад, починаючи з 6\(\cdots\) 7 = 42, то\(42 \div 6 = 7\) і\(42 \div 7 = 6\). Нижче наведено формальне визначення поділу
Визначення: a\(\div\) b визначається як унікальне число, c, за таких умов:\(a \div b = c\) якщо і тільки тоді, коли a = b\(\cdots\) c. If there is no number, c, that exists, or if there is more than one unique number that can be put in for c, then \(a \div b\) вважається невизначеною.
Замість того, щоб писати c, іноді простіше записати пусте або поле в рівняннях, щоб побачити, чи існує унікальне рішення. Якщо ви можете поставити унікальний розв'язок в порожній задачі множення, то ви можете повернутися назад і заповнити розв'язок задачі ділення.
Використовуйте визначення поділу, щоб знайти відповідь на\(\bf 21 \div 3\).
По-перше, зверніть увагу, що\(21 \div 3\) = ____ означає 21 = 3\(\cdots\) _____ По-друге, спробуйте заповнити пробіл в задачі множення унікальним числом, щоб зробити рівняння, 21 = 3\(\cdots\) _____, правда: 21 = 3\(\cdots \underline{7}\). Якщо заповнене число є єдиним можливим рішенням (унікальним), то це відповідь на задачу поділу. Тому\(21 \div 3\) =\(\underline{7}\). Вам не потрібно писати цей абзац для вашого рішення. Нижче наведено, як написати рішення.
Рішення
З тих пір\(21 = 3 \cdots \underline{7}\)\( 21 \div 3 = \underline{7}\).
Скористайтеся визначенням ділення, щоб знайти наступні коефіцієнти:
| а.\(32 \div 8\) |
| б.\(56 \div 8\) |
| c.\(32 \div 2\) |
| д.\(0 \div 13\) |
| е.\(12 \div 1\) |
| f.\(X \div 1\) (Припустимо, що X - будь-яке число.) |
| g.\(0 \div Y\) (Припустімо, Y - будь-яке ненульове число. |
Вправа 25f ілюструє, що будь-яке число, розділене на 1, само собою.
Іншими словами,\(\bf a \div 1 = a\) для всіх значень a.
Вправа 25g ілюструє, що нуль ділиться на будь-яке ненульове ціле число дорівнює 0.
Іншими словами\(\bf 0 \div a = 0\), для всіх ненульових значень a.
У вищезгаданій задачі всі відповіді були цілими числами. Якби вам було запропоновано використовувати визначення для пошуку лише цілих числових рішень, то деякі ділення будуть невизначені під цілими числами. Однак можуть бути раціональні або нераціональні рішення залежно від проблеми.
Використовуйте визначення ділення, щоб знайти, чи\(\bf 21 \div 5\) визначено під цілими числами. Покажіть рішення, якщо воно визначено, або поясніть, чому ні, якщо воно не визначено.
По-перше, зверніть увагу, що\(21 \div 5\) = ____ означає 21 = 5\(\cdots\) _____ По-друге, спробуйте заповнити пробіл в задачі множення єдиним цілим числом, щоб рівняння, 21 = 5\(\cdots\) _____, істинним. Немає цілого числа, яке можна поставити в порожній, щоб зробити це рівняння істинним. Тому не\(21 \div 5\) визначається під цілими числами. Ось як би ви показали відповідь.
Рішення
Оскільки немає цілого числового рішення, щоб зробити рівняння, 21 = 5\(\cdots\) ____\( 21 \div 5\) істинним, не визначається під цілими числами.
Використовуйте визначення ділення, щоб знайти, які з наступних коефіцієнтів визначені під цілими числами. Покажіть рішення, якщо воно визначено, або поясніть, чому ні, якщо воно не визначено. Частина a і b зроблені для вас. Використовуйте їх як приклади.
|
а.\(45 \div 5\) Рішення: З тих пір\( 45 = 5 \cdots \underline{9}\)\(45 \div 5 = \underline{9}\). |
|
б.\(42 \div 9\) Рішення: Оскільки не існує цілого числового рішення, щоб зробити рівняння, 42 = 9\(\cdots\) ___ true, не\(42 \div 9\) визначається під цілими числами. (Так, ви повинні написати все це!) |
|
c.\(48 \div 6\) Рішення: |
|
д.\(35 \div 4\) Рішення: |
|
е.\(48 \div 1\) Рішення: |
|
ф.\(55 \div 7\) Рішення: |
|
г.\(0 \div 8\) Рішення: |
Давайте вивчимо, що відбувається, коли ми ділимося на нуль.
Використовуйте визначення ділення, щоб знайти частку:\(\bf 8 \div 0\).
По-перше, зверніть увагу, що\(8 \div 0\) = ____ означає 8 = 0\(\cdots\) _____ По-друге, спробуйте заповнити пробіл в задачі множення унікальним числом, щоб рівняння, 8 = 0\(\cdots\) _____, істинним. Немає числа, яке можна поставити в порожній, щоб зробити це рівняння істинним, оскільки будь-яке число разів 0 дорівнює 0, і ніколи не дорівнюватиме 8. Ось як ви могли б написати рішення:
Рішення
Немає числа, яке зробить рівняння, 8 = 0\(\cdots\) ____ істинним, оскільки будь-яке число, поставлене в порожнє, зробить праву частину рівняння нулем, що ніколи не може дорівнювати лівій стороні рівняння, яка дорівнює 8. Тому\( 8 \div 0\) не визначено.
Використовуйте визначення ділення, щоб показати, що наступні коефіцієнти не визначені:
а.\(6 \div 0\)
б.\(18 \div 0\)
c.\(M \div 0\) (Припустимо\(M \neq 0\))
У вправі 27 ви показали, що ділення ненульового числа на 0 не визначено. Тепер давайте вивчимо, що станеться, якщо розділити нуль на нуль.
Використовуйте визначення ділення, щоб знайти частку:\(0 \div 0\).
По-перше, зверніть увагу, що\(0 \div 0\) = ____ означає 0 = 0\(\cdots\) _____ По-друге, спробуйте заповнити пробіл в задачі множення унікальним числом, щоб рівняння, 0 = 0\(\cdots\) _____, істинним. Немає унікального числа, яке можна поставити в порожній, щоб зробити це рівняння істинним, оскільки будь-яке число, розміщене в порожньому, зробить рівняння істинним, і тому немає унікального числа, яке працюватиме. Ось як ви могли б написати рішення:
Рішення
Немає унікального числа, яке можна поставити в порожнє, щоб рівняння 0 = 0\(\cdots\) ____ істинним, оскільки будь-яке число зробить його істинним. Тому\(0 \div 0\) називається індетермінантний.
У вправі 27 ви показали, що ненульове число, поділене на нуль, не визначено. Наступний приклад показав, що нуль, ділений на нуль, є невизначеною.
Щоб довести, що ділення на нуль не визначено, необхідно показати два випадки. Нижче наведено повний доказ того, що поділ на нуль не визначено.
Задача: Доведіть, що ділення на нуль не визначено
Рішення: Мета полягає в тому, щоб показати, що\(a \div 0\) не визначено для всіх значень a. Існує два випадки для розгляду випадку 1:\(a \neq 0\); Випадок 2: a = 0.
Випадок 1: Нехай\(a \neq 0\). Немає унікального числа, яке можна було б поставити в порожній, щоб зробити рівняння, a = 0\(\cdot\) ____, істинно, тому що ліва сторона рівняння не дорівнює нулю (так як\(a \neq 0\)), і будь-яке число, поставлене в порожнє, зробить праву частину рівняння нулем. Тому коли\(a \neq 0\),\(a \div 0\) не визначено.
Випадок 2: Нехай a = 0. Немає унікального числа, яке можна поставити в порожнє, щоб рівняння 0 = 0\(\cdot\) ____ істинним, оскільки будь-яке число зробить його істинним. Тому\(0 \div 0\) є невизначеною.
Потрібна практика написання цього доказу. Вам потрібно буде потренуватися в написанні його кілька разів, щоб освоїти проблему. Один з варіантів - запам'ятати докази, показані вище, виписавши його кілька разів, поки ви дійсно не отримаєте ідею. Це зробило б гарне питання іспиту.
Доведіть, що ділення на нуль не визначено.
