1.5: Домашнє завдання
- Page ID
- 66896
- Надіслати домашнє завдання окремо від цієї робочої книги і скріпити всі сторінки разом. (Один штапель для всього подання всіх домашніх завдань блоку)
- Запустіть новий модуль на лицьовій стороні нової сторінки і напишіть номер модуля у верхній частині сторінки.
- Відповіді без підтримки роботи не отримають кредиту.
- Деякі рішення наведені в посібнику з вирішення.
- Ви можете працювати з однокласниками, але робити свою власну роботу.
Нехай U = {a, c, e, m n, r, u, v, w, x, z} з підмножинами A, B, C і D визначеними нижче: A = {m, n, r, u, x} B = {a, c, r, u, x} C = {e, v, w, x, z} D = {a, c, z} Використовуючи правильні позначення, знайти наступне, показати всі роботи
| а.\(\bf B \cap D\) | ф.\(\bf A - C^{c}\) | к.\(\bf (A \cap D) - B^{c}\) |
| б.\(\bf A \cap D\) | г.\(\bf B - (A \cap C)\) | л. н (\(\bf A \cup B\)) |
| c. С - Б | ч.\(\bf D^{c} - (B \cup C)\) | м. п (А) + п (В) |
| д.\(\bf (A \cup C)^{c}\) | я.\(\bf (A \cap B) \cap (C \cup D)\) | п. н (Д - С) |
| е.\(\bf D^{c} \cap B\) | Дж.\(\bf (B^{c} \cup D)^{c}\) | о. н (1\(\bf B \cap C\)) |
Нехай U = {a, c, e, m n, r, u, v, w, x, z} з підмножинами A, B, C визначеними наступним чином:
| A = {m, n, r, u, v} | B = {r, u, ш, х} | C = {n, r, х, с} |
Намалюйте діаграму Венна і розмістіть кожен елемент Всесвіту в правильному регіоні
Використовуйте закони DeMorgan, щоб переписати кожне з наведених нижче дій:
| а.\(\bf N \cup P^{c}\) | б.\(\bf R^{c} \cap S\) |
Використовуйте розподільні властивості множин, щоб переписати кожне з наведених нижче дій:
| а.\(\bf (A^{c} \cup E) \cap (A^{c} \cup F)\) | б.\(\bf B \cap (A \cup C)\) |
Було проведено опитування, щоб визначити, який із трьох напоїв (чай, молоко та/або кава) люди пили щодня. Результати були наступними:
| 7 тільки випив каву | 6 випив всі три | 11 випив чай і каву |
| 21 випив каву | 4 не випив жоден з трьох | 9 не пив ні кави, ні чаю |
| 21 випив чай | 1 пив тільки чай і молоко |
| а. намалюйте діаграму Венна, яка вказує, скільки людей буде належати в кожному регіоні. Позначте три набори значущими літерами. |
| б. скільки людей було обстежено? |
| c. скільки пили молока? |
| d. скільки пили тільки каву і молоко? |
| е Скільки пили тільки молока? |
| f Скільки пили чаю або кави, але не молока? |
| м Скільки пили рівно два види напоїв? |
| h Скільки не пили молока чи чаю? |
Вийміть свої блоки A - і організуйте їх у підмножини так, щоб кожна підмножина містила лише елементи, які мають однаковий розмір і колір.
| a Скільки підмножин існує? | б Скільки штук в кожній підмножині? |
Нехай A, B і C представляють будь-які множини. Відповідь True або False для наступних тверджень. Для того щоб твердження було правдою, воно завжди повинно бути правдою. Для кожного помилкового твердження наведіть приклад того, чому це False.
| а. B завжди є підмножиною\(\bf A \cup B\) |
| б.\(\bf (A - B)^{c} = A^{c} - B^{c}\) |
| c. B завжди є підмножиною\(\bf A \cap B\) |
| г.\(n\) (\(\bf A \cup B\)) =\(n\) (А) +\(n\) (Б) |
| е.\(n\) (\(\bf A \cup B)\)=\(n\) (А) +\(n\) (В) —\(n\) (\(\bf A \cap B\)) |
| f Якщо\(n\) (\(\bf A \cup B\)) =\(n\) (A) +\(n\) (B), то A і B нероз'єднані. |
Намалюйте діаграму Венна і затіньте в області, яка представляє наступне
| а.\(\bf (C \cup A) - B\) | б.\(\bf (C \cap B) \cup A\) | c.\(\bf (C \cap B) - A\) |
| д.\(\bf (A \cup C) \cap B\) | е.\(\bf \bar{A} - (B \cap C)\) | ф.\(\bf (B - A) \cap (B - C)\) |
Визначте затінену область кожної діаграми Венна за допомогою встановлених позначень.
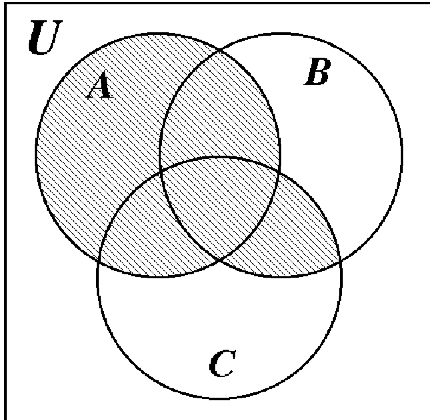 а. а. |
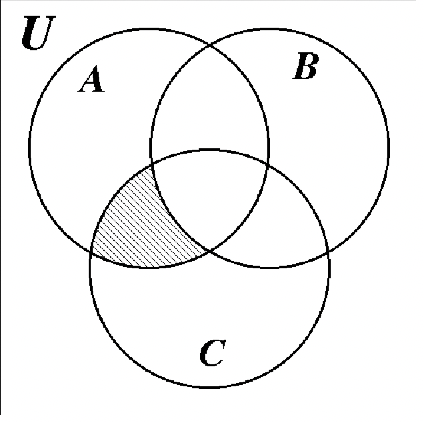 б. б. |
Перерахуйте всі можливі підмножини для кожного заданого набору.
| a. {} | б. {a} | c. {a, b} | d. {a, b, c} |
Нехай A = {1, 2, 4}, B = {(a, c), 5} і C = {x}. Знайдіть наступне:
| а.\(A \times A\) | а.\(A \times B\) | c.\(B \times C\) |
| д.\(C \times A\) | а.\(C \times C\) |
Скористайтеся блоками A - для вирішення цієї проблеми. Нехай X представляють набір великих кіл, а Y представляють набір червоних кіл. Використовуючи множину позначень і абревіатур, знайдіть наступне:
| а. X - Y | б.\(\bf X \cap Y\) | c.\(\bf X \cup Y\) | д. Y - Х |
