1.4: Проблеми опитування

У цьому наборі вправ ви не будете працювати з маніпуляціями. Ми будемо будувати та використовувати діаграми Венна по-іншому, щоб відповісти на конкретні питання, враховуючи різноманітну інформацію.

Ми збираємося почати з навчання, як побудувати два набір діаграма Венна, де

U = {1, 2, 3, 4, 5, 6, 7, 8, 9},

A = {1, 2, 3, 4, 5} і

B = {2, 4, 6, 8}.

Мета полягає в тому, щоб побудувати діаграму Венна, яка показує розміщення всіх елементів у Всесвіті.

Зверніть увагу, що пуста діаграма Венна з двома наборами має чотири окремі області.

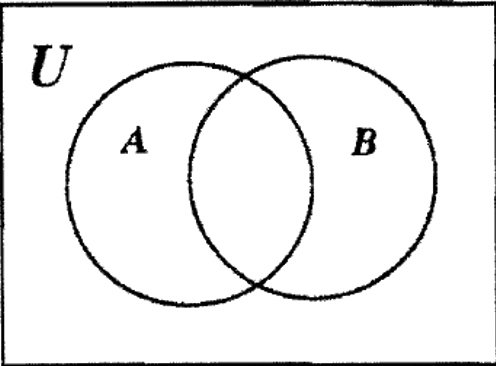
Спосіб 1

Один із способів отримати рішення - вирішити, де розмістити кожне число, по одному за раз. Починаючи з 1, зверніть увагу, що він знаходиться лише у наборі A, і розмістіть його в цій області (яка номінально є A — B). Потім ви можете з'ясувати, де розташувати кожен з інших восьми елементів по одному. Не має значення, який елемент ви розміщуєте першим. Але, врешті-решт, кожен з дев'яти елементів необхідно розмістити в одній з чотирьох областей. Спробуйте скористатися цим методом. Помістіть кожен з дев'яти елементів на діаграмі Венна, показану вище.

Спосіб 2

Ось ще один спосіб отримання розчину. Оскільки ми можемо обчислити, що\(\bf A \cap B\) = {2, 4}, ми можемо розмістити ці два елементи на перетині відразу, і ми знаємо, що ніякі інші числа не йдуть туди.

Далі ми зауважимо, що A також містить елементи 1, 3 і 5, тому тепер ми можемо заповнити ці елементи в іншій області A. Аналогічно, ми зауважимо, B також містить 6 і 8, тому ми можемо заповнити ці елементи в іншій області B. Це показано нижче.

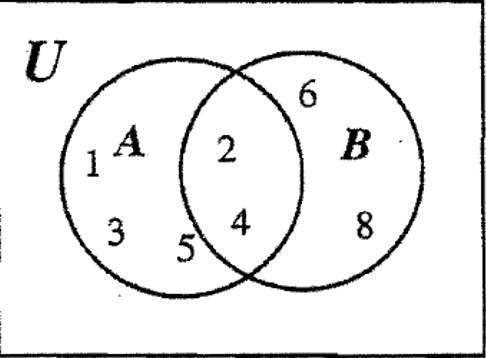
Єдині елементи у Всесвіті, які не враховуються, - це 7 і 9. Вони йдуть у частині Всесвіту, яка не містить A або B. Після введення їх, всю діаграму можна завершити, як показано нижче. Щоб перевірити, чи відповідає вихідна інформація, надана вище, з відповіддю.

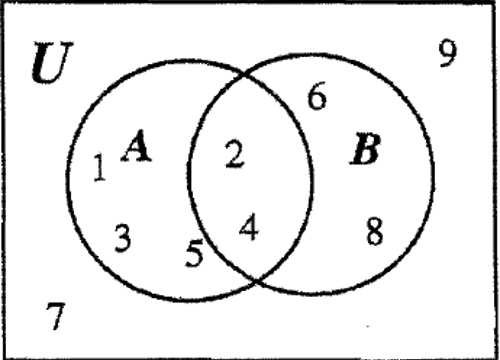
Чи змогли ви отримати правильну відповідь, як показано вище, використовуючи перший запропонований метод?

Вправа 1

Помістіть кожен елемент Всесвіту у своїй правильній області на діаграмі Венна праворуч, якщо U = {1, 2, 3, 4, 5, 6, 7, 8, 9}, A = {2, 4, 5,7, 9} і B = {1, 2, 5, 6}

У наступному прикладі інформація надається в іншій формі. Спосіб 1 дуже складний у використанні, коли множини A і B явно не задані. Ми все одно повинні бути в змозі заповнити діаграму Венна. Знову ж таки, ми будемо працювати з двома наборами A і B. На завершення відповімо на ці питання: Які елементи є в A, B і U? Наведено таку інформацію: A — B = {c, d},\(\bf B^{c}\) = {b, c, d, e, f}, B — A = {a, g} і\(\bf A \cup B\) = {a, c, d, g, h}

КРОК 1: Оскільки A - B і B - A обидва ізольовані регіони, ми могли б почати з заповнення цієї інформації на порожній діаграмі Венна, як показано нижче:

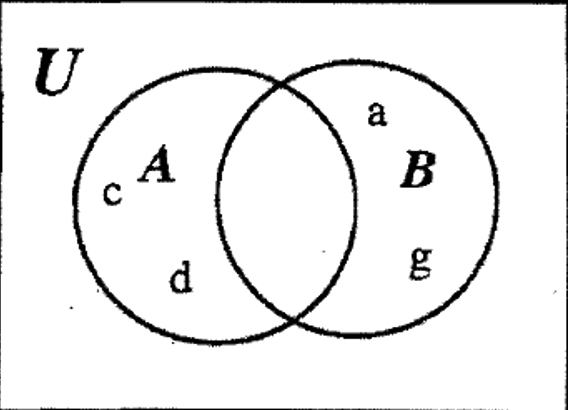
КРОК 2: Далі ми можемо заповнити решту\(\bf A \cup B\), поставивши елемент h в перетин, область ще не врахована.

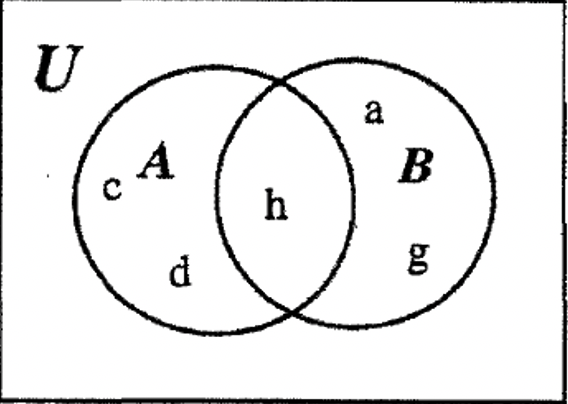
КРОК 3: Нарешті, ми можемо заповнити решту\(\bf B^{c}\). Зауважте, що поки що ми бачимо елементи c і d в одній з областей\(\bf B^{c}\), тому інші елементи b, e і f повинні йти в єдиний регіон, який ще не враховується, як показано:

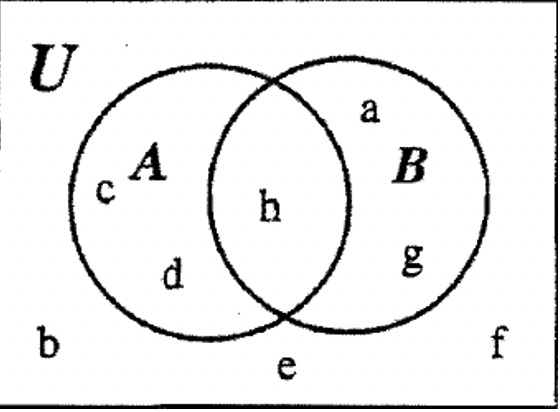
КРОК 4: Переконайтеся, що інформація, надана на початку проблеми, все ще вірна при перегляді готової діаграми Венна, як показано вище.

КРОК 5: Дайте відповідь на поставлені запитання:

U = {a, b, c, d, e, f, g, h}

A = {c, d, h}

B = {a, g, h}

Зверніть увагу, що хтось інший міг зробити вищезазначену проблему за допомогою різних кроків. Існує більше ніж один спосіб продовжити і все ще прийти до правильного рішення. Ви повинні спробувати його ще раз на свій розсуд. Результат повинен бути однаковим незалежно від того, який регіон ви заповнили першим.

Ми зробимо ще один приклад такого типу, але цього разу ми будемо працювати з трьома встановленими діаграмами Венна. Так як регіонів вісім, будівництво займе трохи більше часу. Наведена інформація наступна:\(\bf (A \cap B) - C\) = {h}, B — C = {h, n},\(\bf (A \cup B) - C\) = {l, m, h, n}, A — B = {l, m, f},\(\bf A \cap B\) = {g, h, i}, B = {h, n, j, g, i}, C = {f, g, i, j, k} і\(\bf (C \cup B)^{c}\) = {l, m, d, e}

Нижче наведено лише один із способів вжити заходів, які призводять до правильної відповіді.

КРОК 1: Спочатку подивіться на порожню діаграму Венна з трьома встановленими та знайдіть ізольовану область, яку ви можете заповнити спочатку з наданої інформації. \(\bf (A \cap B) - C\)задовольняє цьому критерію і, таким чином, цей регіон може бути заповнений першим, як показано нижче.

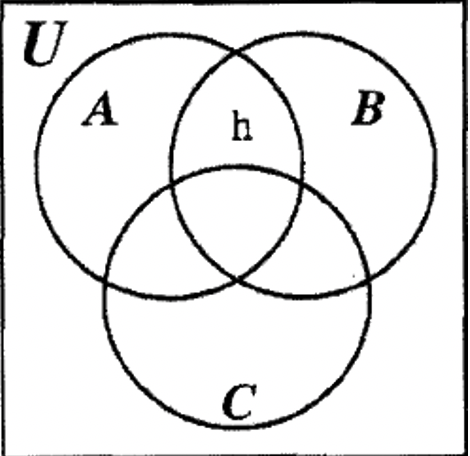
КРОК 2: Далі, B - C можна завершити, помістивши елемент n в область, ще не заповнену, як показано нижче.

КРОК 3:\(\bf A \cap B\) може бути заповнений зараз теж з g і я йду в регіон ще не врахований:

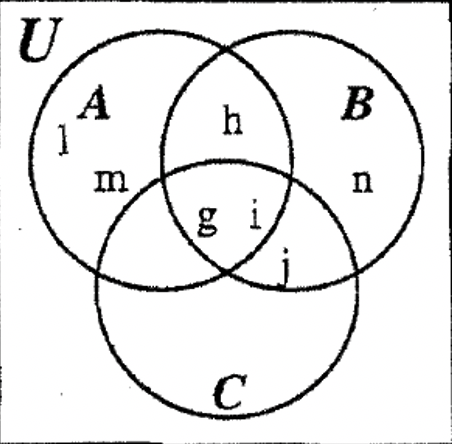
КРОК 4: Далі ми можемо заповнити обидва\(\bf (A \cup B) - C\) і B, оскільки вони також зводяться до ізольованих регіонів.

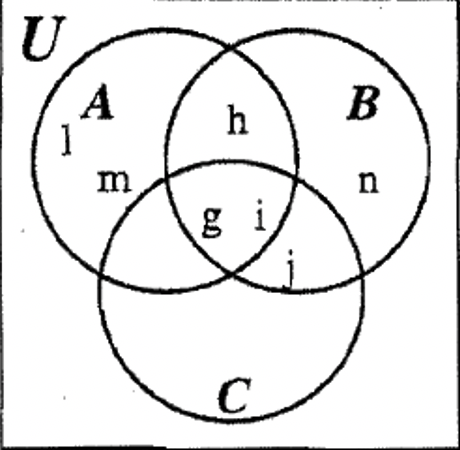
КРОК 5: Ми наближаємося. Залишилося заповнити лише три регіони. \(\bf (C \cup B)^{c}\)а решту області A - B можна заповнити, як показано нижче:

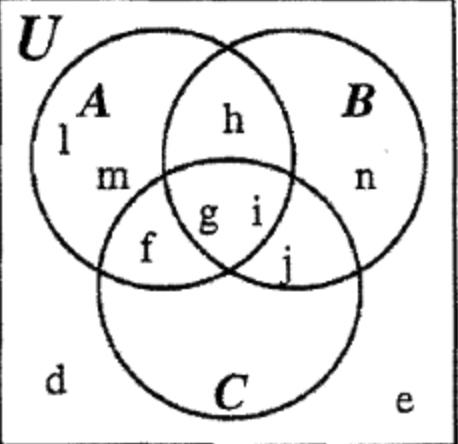
КРОК 6: Тепер ми можемо заповнити решту області набору C, щоб завершити діаграму.

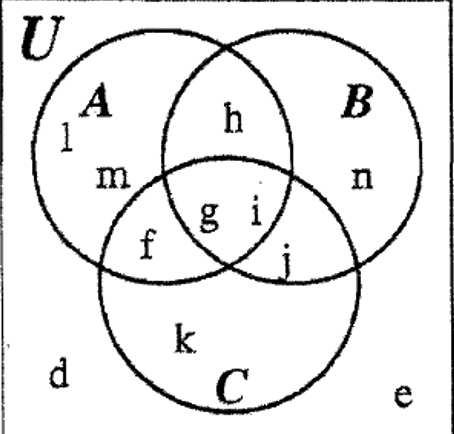
КРОК 7: Перевірте, щоб переконатися, що вся надана інформація все ще відповідає дійсності при перегляді цієї готової діаграми. Тепер ми можемо констатувати елементи в наборах A, B, C і U.

U = {d, e, f, g, h, i, j, k, l, m, n}	A = {f, g, h, i, л, м}
B = {g, h, i, j, n}	C = {f, g, i, j, k}

Вправа 2

Враховуючи, що U = {a, b, c, d, e, f, g, h, i, j, k}, X = {a, b, c, d, e}, Y = {c, d, f, g, h} і Z = {b, c, h, i, j}, заповніть кожен з елементів Всесвіту в її належній області на діаграмі Венна праворуч.

Вправа 3

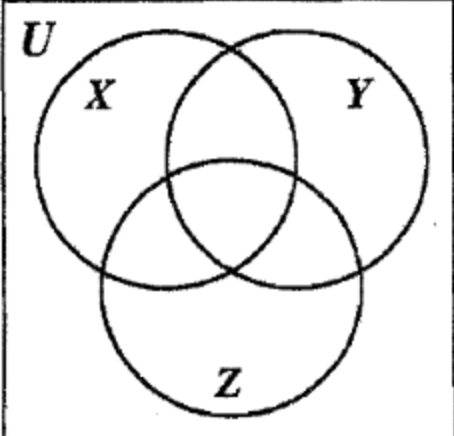
Зараз настав час для вас, щоб потренуватися в ідентифікації восьми областей з трьох наборів діаграми Венна, описуючи кожну область за допомогою множини. Опишіть кожну область, як зазначено в дужках на діаграмі Венна. Там може бути більше одного способу опису регіону.

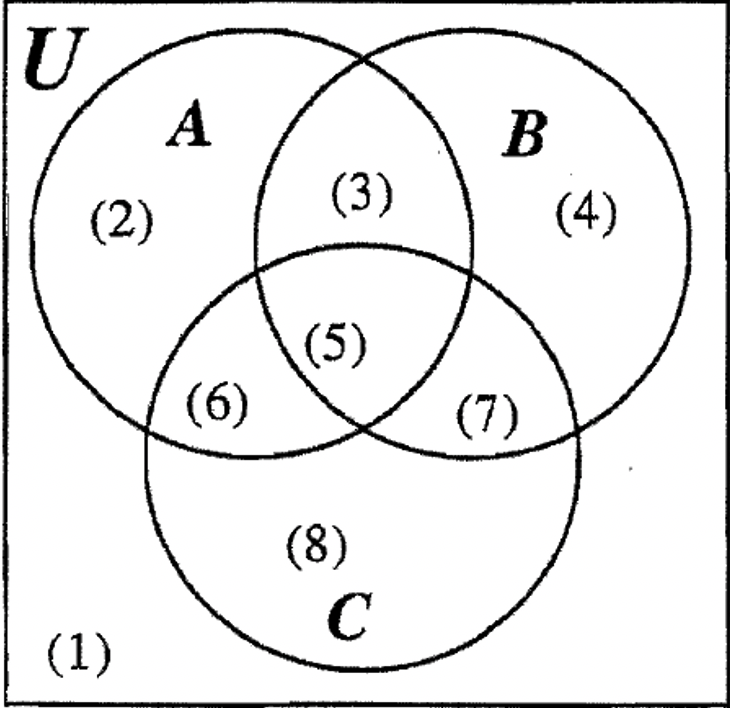
a. регіон 1: _____

б. регіон 2: _____

c Регіон 3: ______

д. регіон 4: ______

е Регіон 5: ______

f Регіон 6: ______

г Регіон 7: ______

h. Регіон 8: _______

Перш ніж перейти до обстеження проблем типу, нам потрібно потренуватися, дивлячись на діаграму Венна, де дається кардинальність (кількість елементів) кожного регіону, а потім мати можливість відповісти на питання про кардинальність інших комбінацій регіонів.

Вправа 4

Подивіться на діаграму Венна нижче і дайте відповідь на питання про кардинальності зазначених регіонів.

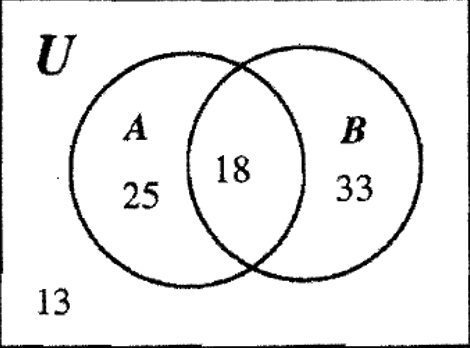
а.\(n\) (А) = ____	б.\(n\) (Б) = ____
с.\(n\) (\(\bf A^{c}\)) = ____	d.\(n\) (\(\bf B^{c}\)) = ____
е.\(n\) (\(\bf A \cap B\)) = ____	ф.\(n\) (А — Б) = ____
г.\(n\) (\(\bf (A \cup B)^{c}\)) = ____	ч.\(n\) (U) = ____

Уявіть, що вищевказана проблема була дійсно моделлю для того, які фрукти група людей упаковувала в свої обіди. А стояв для тих, хто упаковував яблука, а Б стояв для тих, хто упаковував банани. Припустимо, яблука і банани є єдиним видом фруктів, доступних. Тоді питання, на які ви відповіли, були такими:

1. Скільки упаковані яблука?
2. Скільки упакованих бананів?
3. Скільки не упакували яблук?
4. Скільки не упакували бананів?
5. Скільки упаковані обидва види фруктів?
6. Скільки тільки упакованих яблук?
7. Скільки не упакували жодного фрукта?
8. Скільки людей було обстежено?

Подивіться, чи заглянули б ви в ті ж регіони, якби питання задавалися таким чином.

Вправа 5

Давайте подивимося, наскільки добре ви працюєте з трьома встановленими діаграмами Венна. Діаграма Венна нижче показує кардинальність кожного регіону. Опитування студентів коледжу показало оцінки, які вони отримали на своїй останній табелі. Стенди для отримання A, B розшифровується як отримання B і C означає отримання C. Деякі люди взяли тільки один курс, тоді як інші взяли більше. Подивіться на діаграму Венна і дайте відповідь на наступні питання. Додатковий кредит: Замість того, щоб просто писати номер, запишіть, що питання задається символічно. Іншими словами, якщо питання «Скільки отримали як A, так і B?» Ви б написали\(n\) (\(\bf A \cap B\)) = 51.

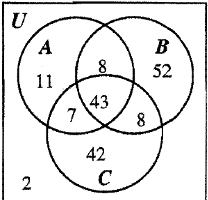
а Скільки отримали всі А? ____

б Скільки отримав A? ____

c Скільки отримали B і C? ____

d Скільки отримали тільки A або B? _____

е Скільки не отримав C? _____

f Скільки отримали B або C? _____

г Скільки отримав B, але не C? ____

h Скільки отримали принаймні два різних класи A, B або C? ____

i. скільки отримали рівно два різних класи A, B або C? ____

Вправа 6

В іншому опитуванні задавалися питання, щоб побачити, скільки людей було в підлітковому віці, скільки одружилися і скільки мали дітей. T представляє підлітків, М представляє тих, хто був одружений, а С - тих, хто має дітей. Подивіться на діаграму Венна, яка показує кардинальність кожного регіону, щоб відповісти на наступні питання:

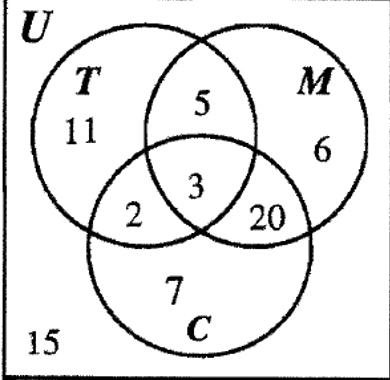
1. Скільки людей вийшло заміж? ____
2. Скільки підлітків мали дітей? ____
3. Скільки людей було в опитуванні? ____
4. У скількох людей не було дітей? ____
5. Скільки підлітків не були одружені? ____
6. Скільки підлітків було одружено з дітьми? ____
7. Скільки підлітків було в опитуванні? ____
8. Скільки людей були неодружені з дітьми? ____
9. Скільки людей було одружено з дітьми? ____

На початку цього набору вправ ви дізналися, як розміщувати елементи у відповідних областях, задавши інформацію про елементи в деяких наборах. Цей же процес можна використовувати тільки при розгляді кардинальності набору або регіону. Ми зробимо приклад за участю двох множин, C і B, де\(n\) (U) = 35,\(n\) (C) = 20,\(n\) (B) = 15 і\(n\) (B — C) = 10.

КРОК 1: Знову ж таки, ми спочатку повинні ізолювати регіон. B - C є ізольованою областю, і тому ми можемо заповнити 10 в цьому місці, як показано в Венні нижче:

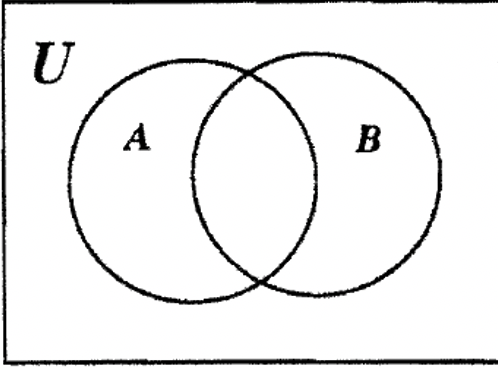
КРОК 2: Ми можемо заповнити 5 в іншу область B, оскільки B має загалом 15 елементів (10 + 5 = 15).

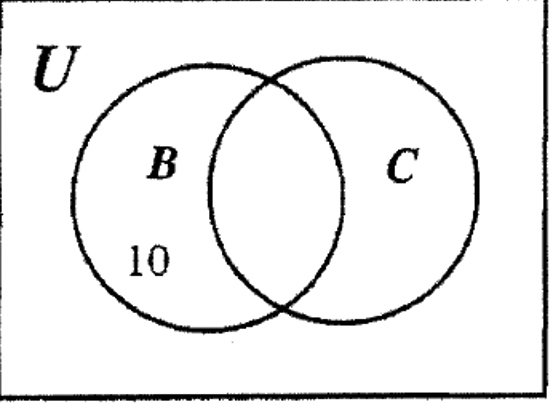
КРОК 3: Оскільки C має загалом 20 елементів, ми можемо заповнити іншу область C числом 15.

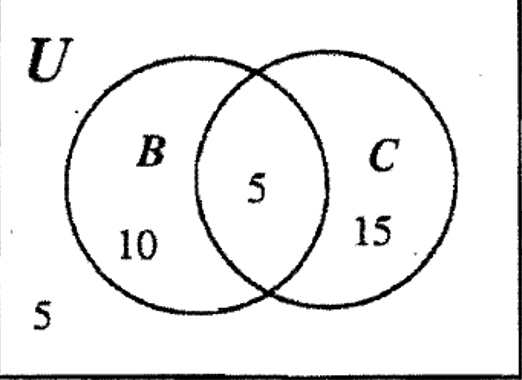
КРОК 4: Залишається лише одна область для заповнення, і оскільки загальна кількість елементів становить 35, кінцева область для заповнення повинна бути 5.

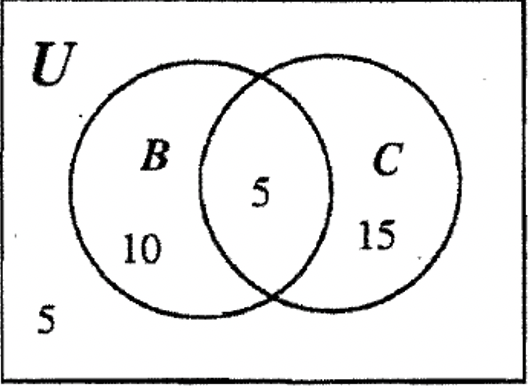
Як правило, вищезгадана проблема була б проблемою слова, сформульована приблизно так:

Було обстежено клас з 35 студентів, і було визначено, що 20 студентів володіли автомобілем, 15 володіли велосипедом, а 10 з тих, хто володіє велосипедом, не мають автомобіля. Скільки студентів володіли і велосипедом, і автомобілем? Скільки студентів володіло тільки автомобілем? Скільки студентів не володіли ні велосипедом, ні автомобілем?

Для того, щоб відповісти на ці питання, можна розглянути можливість складання діаграми Венна, що містить два набори, C і B, де C буде представляти кількість студентів, що володіють автомобілями, а B буде представляти кількість студентів, які володіють велосипедами. Зверніть увагу, перший крок буде у визначенні змінних! Далі, прочитавши надану інформацію, можна зробити висновок, що інформація може бути записана символічно так:\(n\) (U) = 35,\(n\) (C) = 20,\(n\) (B) = 15 і\(n\) (B — C) = 10. Це виглядає знайомим? Звідси кроки будуть точно такими ж, як ми тільки що робили у наведеному вище прикладі. Потім людина могла подивитися на діаграму Венна і відповісти на поставлені запитання.

• Скільки студентів володіли і велосипедом, і автомобілем? (Подивіться на\(\bf B \cap C\)):\(\underline{5}\)
• Скільки студентів володіло тільки автомобілем? (Подивіться на C — B)):\(\underline{15}\)
• Скільки студентів не володіли ні велосипедом, ні автомобілем? (Подивіться на\((\bf B \cup C)^{c}\)):\(\underline{5}\)

Вправа 7

Двадцять дошкільнят були опитані про те, чи є у них собаки та/або коти в якості домашніх тварин у своєму будинку. Десять дітей володіли обома тваринами. Чотири не мали домашніх тварин вдома і 14 володіли собаками. Побудуйте діаграму Венна, яка відображає, скільки було кожного виду тварин, і дайте відповідь на поставлені запитання на основі вашої діаграми. Використовуйте значущі літери, щоб представити свої набори!

а. скільки дітей володіли кішками?

б. скільки дітей володіли тільки котами?

c Скільки дітей не володіли собакою?

Настав час потренуватися в побудові діаграми Венна з трьома множинами, враховуючи наступну інформацію про три набори, A, B і C:

\(n\)(\(\bf (A \cap B) - C)\)= 2	\(n\)(В — С) = 8
\(n\)(А — Б) = 7	\(n\)(А) = 13
\(n\)(\(\bf A - (B \cup C)\)) = 4	\(n\)(Б) = 20
\(n\)(С — В) = 13	\(n\)(У) = 42

Ми побудуємо діаграму Венна, яка показує кардинальність кожного регіону, а потім знайдемо:

а.\(n\) (\(\bf (B \cap C)\))

c.\(n\) (\(\bf B^{c}\))

е.\(n\) (\(\bf (A \cup C) - B\))

ф.\(n\) (\(\bf (C - (A \cup B)\)

г.\(n\) (А)

ч.\(n\) (\(\bf (A \cup B \cup C)^{c})\)

б.\(n\) (А — С)

г.\(n\) (С)

КРОК 1: Намалюйте три набори діаграми Венна і подивіться, чи є якась із наданої інформації достатньо конкретною, щоб охопити лише одну область. \(\bf (A \cap B) - C\)і\(\bf A - (B \cup C)\) кожен охоплює один регіон, тому спочатку заповніть ці регіони.

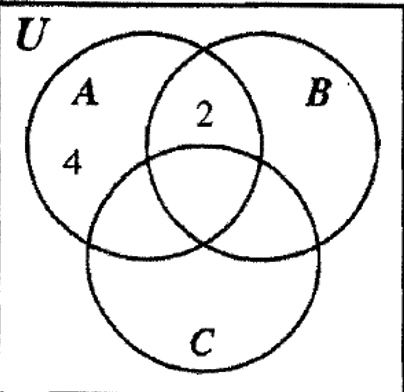
КРОК 2: B - C і A - B мають дві області з однією областю кожного вже заповненого. Дві області B — C повинні скласти до 8 так, щоб залишалося 6 для іншої частини. Аналогічно, дві області A — B повинні скласти до 7, залишаючи 3 для іншого регіону.

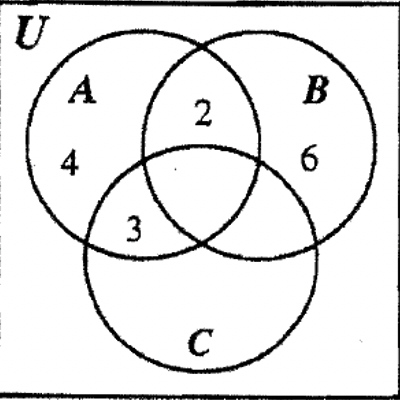
КРОК 3: A має три з чотирьох областей заповнені зараз, тому ми можемо заповнити 4 в останній області A, оскільки\(n\) (A) = 13, що означає, що всі чотири області A повинні скласти до 13.

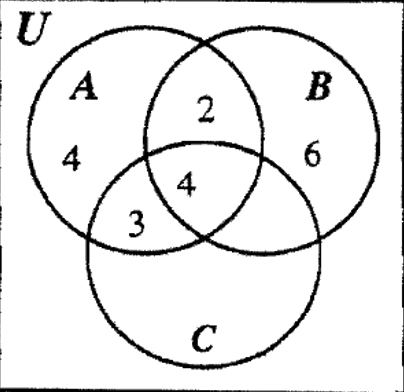
КРОК 4: Зверніть увагу, що B має всі області, крім однієї, заповнені зараз, тому ми можемо заповнити цю останню область з 8 оскільки\(n\) (B) = 20.

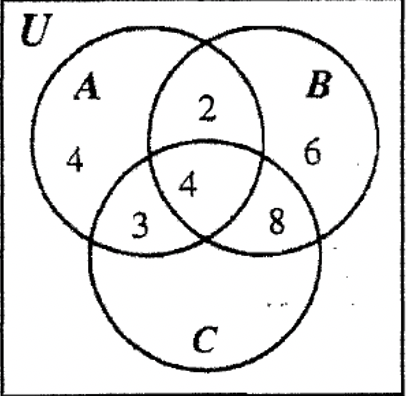
КРОК 5: Оскільки\(n\) (C - B) = 13 і одна з двох областей C - B дорівнює 3, що залишає 10 для заповнення в іншу область.

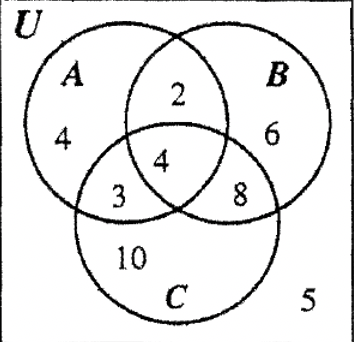
КРОК 6: Залишилося заповнити лише одну область, і оскільки Всесвіт містить 42 елементи, залишилося враховувати 5 елементів. На цьому ця частина процесу закінчена.

КРОК 7: Цей крок дуже важливий! Переконайтеся, що ви повернетеся назад і перевіряєте свою роботу дуже ретельно. На початку проблеми було надано вісім відомостей. Поверніться назад і перевірте кожен окремо. Наприклад, переконайтеся, що коли ви дивитеся на завершену діаграму, все ще вірно, що\(n\) (B — C) = 8,\(n\) (A — B) = 7,\(n\) (A) = 13,\(n\) (\(\bf A - (B \cup C)\)) = 4,\(n\) (C — B) = 13 тощо.

КРОК 8: Подивіться на завершену діаграму Венна і тепер дайте відповідь на поставлені питання:

а.\(n\) (\(\bf B \cap C\)) = 12

б.\(n\) (А — С) = 6

с.\(n\) (\(\bf B^{c}\)) = 22

г.\(n\) (С) = 25

е.\(n\) (\(\bf (A \cup C) - B\)) = 17

ф.\(n\) (\(\bf (C - (A \cup B)\)) = 10

г.\(n\) (А) = 13

ч.\(n\) (\(\bf (A \cup B \cup C)^{c}\)) =5

Найчастіше вищевказана проблема була б представлена як проблема типу опитування, де відповіді можна було б відповісти за допомогою теорії множин. Розглянемо наступний приклад.

Опитування 42 чоловіків було проведено, запитуючи про те, як їм подобається певні жіночі імена: Емі, Бет та Сінді. Було виявлено, що 13 чоловікам сподобалося ім'я Емі, 20 з них любили Бет, 8 любили Бет, але не Сінді, 13 любили Сінді, але не Бет, 7 любили Емі, але не Бет, 4 сподобалося лише ім'я Емі і 2 сподобалися Емі та Бет, але не ім'я Сінді. Знайдіть наступне:

1. Скільки чоловіків сподобалися як імена Бет, так і Сінді?
2. Скільки чоловіків сподобалося ім'я Емі, але не ім'я Сінді?
3. Скільки чоловіків не сподобалося ім'я Бет?
4. Скільки чоловіків сподобалося ім'я Сінді?
5. Скільки чоловіків не сподобалося ім'я Бет, але сподобалося хоча б одне з інших імен?
6. Скільки чоловіків сподобалося тільки ім'я Сінді?
7. Скільки чоловіків сподобалося ім'я Емі?
8. Скільки чоловіків не сподобалося жодне з імен?

Цю проблему можна було б вирішити, спочатку дозволивши буквам A, B і C представляти набори чоловіків, яким сподобалися імена Емі, Бет і Сінді відповідно. Далі ви можете виписати вісім підказок, заданих за допомогою набору позначень, які дадуть вам точно такі ж вісім підказок, наведених на початку попереднього прикладу! Або ви можете перейти прямо до діаграми Венна, вирішивши, з якою частиною діаграми Венна пов'язана кожна підказка, і почати заповнювати цифри. Задані питання також точно такі ж, як і в попередньому прикладі. Спробуйте цю проблему в цій формі, а потім перевірте свої відповіді, озирнувшись на попередній приклад. Переконайтеся, що ви можете зробити це успішно самостійно, перш ніж спробувати наступні дві вправи.

Вправа 8

Було проведено опитування 60 студентів коледжу, запитуючи про те, які страви вони регулярно їли в школі. Тридцять учнів зазвичай снідали в школі, 26 зазвичай їли там обід

і 23 зазвичай їли вечерю в школі. Шість учнів сказали, що їли всі три прийоми їжі в школі. Одинадцять їли і сніданок, і обід там, тоді як 15 снідали тільки в школі, а 12 їли тільки обід там. Позначте набори та заповніть діаграму Венна нижче, що представляє цю інформацію, і дайте відповідь на наступні питання:

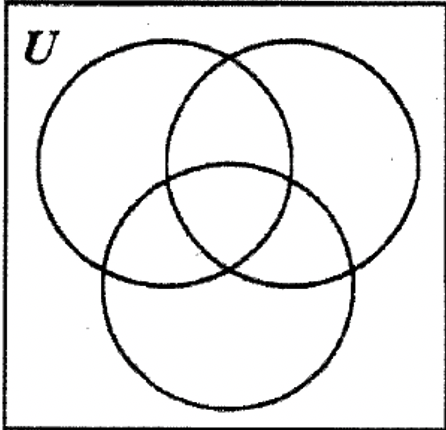
а. скільки учнів з'їли обід і вечерю в школі?

б Скільки не їли жодної їжі в школі?

c Скільки їли лише вечерю в школі?

d Скільки їли сніданок і/або вечерю в школі?

е Скільки з'їли рівно один прийом їжі в школі?

е Скільки їли хоча б дворазове харчування в школі?

м Скільки їли як обід, так і вечерю в школі, але не сніданок?

Вправа 9

Іншу групу студентів запитали, які старі перезапуски Діка Ван Дайка, острова Гіллігана та молодят, які вони любили дивитись на пізній вечір TV. 34 сподобалися як Дік Ван Дайк, так і острів Гіллігана, тоді як 7 сподобався лише Дік Ван Дайк і 11 любив лише острів Гіллігана. 15 сподобався Дік Ван Дайк, але не Гілліган Острів тоді як 21 сподобався острів Гіллігана, але не Дік Ван Дайк. 27 не сподобався молодят, але сподобався принаймні одна з інших програм. 31 не сподобався молодятам, а 20 сподобався молодят, але не острів Гіллігана. Позначте набори та заповніть діаграму Венна нижче, що представляє цю інформацію. Потім дайте відповідь на наступні питання:

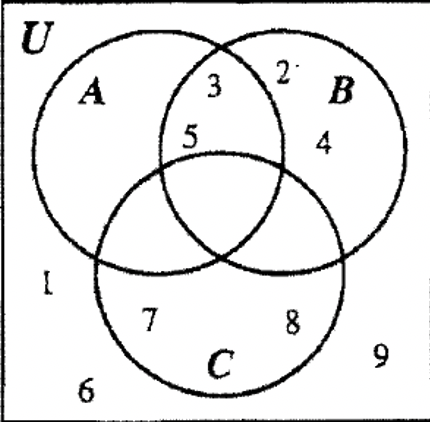
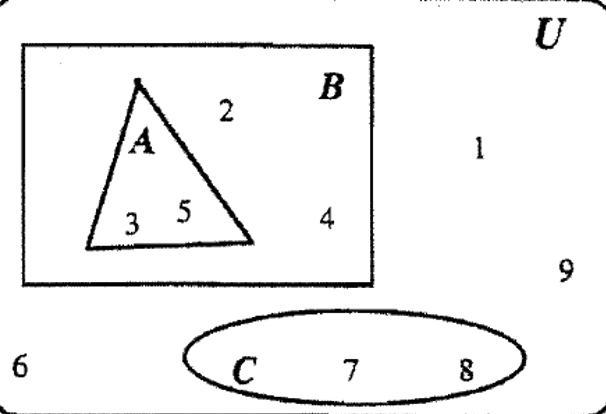
Працюючи з діаграмами Венна досі, ми в основному обмежили зображення трьома наборами і показували один і той же шаблон знову і знову, де набори перекривають один одного. Для конкретної проблеми діаграма Венна може бути представлена зовсім по-різному. Наприклад, розглянемо U = {1, 2, 3, 4, 5, 6, 7, 8, 9} з підмножинами A, B і C визначеними наступним чином:

A = {3, 5}, B = {2, 3, 4, 5} і C = {7, 8}. Ми могли б показати елементи Всесвіту двома способами, показаними нижче. Венн зліва показує звичайний спосіб, як ми робили для цього набору вправ, тоді як той, що праворуч насправді трохи більш конкретним, тому що з малюнка зрозуміло, що\(\bf A \subset B\) і що C не має елементів спільного з A або B.

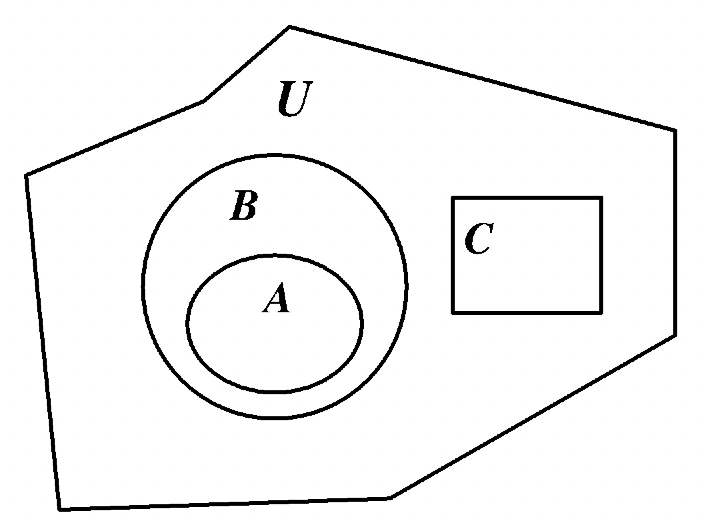
Особливо корисно мати можливість малювати діаграму Венна, подібну до другої діаграми Венна, показаної вище, коли вас попросять зробити щось подібне: Намалюйте діаграму Венна, що містить набори A, B і C, так що\(\bf A \subset B\) з C не має елементів спільного з А або Б. Зверніть увагу, що вам не даються конкретні елементи A і B. Діаграма праворуч показує один із способів представлення цієї інформації.

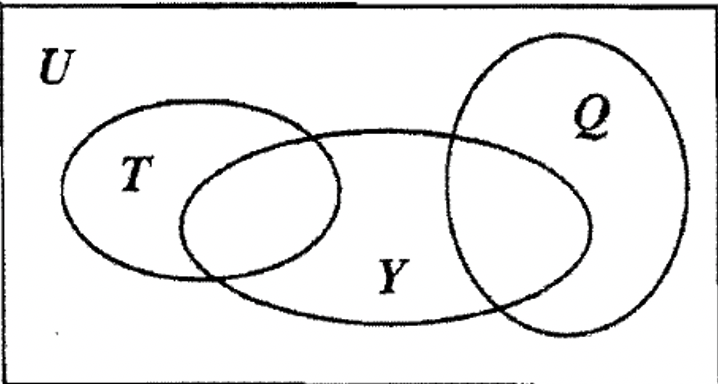
Розглянемо такі підмножини A-блоків: жовтий, трикутник і квадрат. Один із способів показати, як вони можуть бути розташовані на діаграмі Венна, показаний на Венні праворуч. Трикутники і квадрати нез'єднані один з одним, тоді як трикутники і квадрати перетинаються з жовтим.

Вправа 10

У наведеному нижче просторі розташуйте ці підмножини A - блоків, червоного (R), зеленого (G) та Circle (C) на діаграмі Венна, яка чітко показує їх зв'язок один з одним.

Вправа 11

У наведеному нижче просторі розташуйте ці підмножини A - блоків, зеленого (G), жовтого (Y), синього (B), червоного (R), малого (S) у діаграмі Венна, яка чітко показує їх зв'язок один з одним.

Вправа 12

Нехай U = {1, 2, 3, 4, 5, 6, 7, 8, 9} з цими підмножинами: A = {6, 7, 8}, B = {2, 3}, C = {3, 4}, D = {5}, E = {1, 2, 3, 4, 5, 6}. У наведеному нижче просторі розташуйте ці набори на діаграмі Венна, яка чітко показує їх зв'язок один з одним. Це трохи складно, тому що є п'ять підмножин, але ви можете це зробити!