1.3: Детальніше про набори
- Page ID
- 66897
Вам знадобляться: Ножиці, A-Blocks (Material Cards 2A-2E), великий плакат з намальованою на ньому трьома встановленими діаграмами Венна. Якщо у вас немає плаката, подивіться на схему ліворуч. Тире вказують, де ви можете скріпити чотири аркуші паперу або картки (або дві відкриті папки файлів) разом, а потім намалювати велику діаграму Венна з трьома встановленими.
Тепер, коли ви освоїли затінення діаграм Венна (не смійтеся), прийшов час вийти з вашого набору A-блоків (які включають білі карти міток значення). Кожне коло являє собою набір, і ми будемо маркувати кожне коло різними картками значень (білі картки в кожному наборі A-блоків) у різних вправах.
Почніть з вибору значення (конкретного кольору, форми або розміру). Поставте його значення ярлик карти - R червоний, B синій, G зелений, Y жовтий, T трикутник, S Q квадратний, C коло, S маленький або L великий на одному з кіл (що представляє набір) на діаграмі Венна. Помістіть усі A-блоки, що мають це значення (наприклад, усі квадрати) у цьому колі. Залиште ці шматочки там. Тепер вибираємо інше значення і ставимо його ярлик карти на одному з інших кіл. Помістіть всі A-блоки, що мають це друге значення, у цьому другому колі. Зверніть увагу, що кола перекриваються. Переконайтеся, що шматок з одного значення не знаходиться в перекритті, якщо він також не належить до іншого кола. Ви можете використовувати скорочення при відповіді на ці питання.
Якою була ваша перша цінність? ____ Якою була ваша друга цінність? ____
Чи належать якісь твори в обох колах? ____ Якщо так, то які з них? ____
Що ми називаємо перекриттям? ____
Тепер додайте третє значення для третього кола на Венн.
Якою була ваша третя цінність? ____
Розташуйте всі 24 штуки на плакаті так, щоб кожен з них знаходився в правильному регіоні. Зверніть увагу, що на діаграмі Венна є вісім різних регіонів. Деякі шматки можуть бути поза всіма трьома колами. Все залежить від того, які значення ви вибрали. Щоб перевірити себе, подивіться, уважно на кожне коло (який представляє собою набір), по одному. Скажімо, квадрати - це значення, яке ви вибрали для одного кола. У цьому колі чотири регіони. Всі квадрати повинні знаходитися в одному з цих чотирьох місць. Тепер перевірте кожне з наступних двох кіл, по одному. Якщо одне коло мало значення, кожен маленький шматок повинен знаходитися в одній з чотирьох областей цього кола. Останній, ви перевірите третє коло. Більшість людей мають проблеми з отриманням його точно в перший раз через. Просто працюйте, поки не будете задоволені, кожен елемент знаходиться на своєму належному місці. Переконайтеся, що всі 24 штуки враховуються і що ви перевіряєте свою роботу, розглядаючи кожен набір окремо. Потім на порожній діаграмі Венна, показаній у верхній частині наступної сторінки, використовуйте скорочення, щоб позначити, де розміщувався кожен шматок. Крім того, позначте кожне коло значенням, яке ви вибрали для цього набору. Скільки різних регіонів існує в трьох встановлених діаграмах Венна? ____ (Підказка: подивіться на початок цього абзацу для відповіді.)
Якщо у вас виникли проблеми з цією першою вправою, ви можете вивчити діаграму Венна нижче. Вибрані мітки значень були RED (R), BLUE (B) та CIRCLE (C). A - блоки відображаються у правильній області. Зверніть увагу, що є два з восьми областей, які є порожніми. Це тому, що жоден елемент не є як червоним, так і синім! Показані скорочення для блоків A. Для перевірки орієнтуйтеся на один набір (коло) за раз. Всі червоні шматочки і ніякі інші не повинні бути в наборі з маркуванням RED. Всі сині шматочки і ніякі інші не повинні бути в наборі з позначкою BLUE і всі кола, і жоден інший не повинен бути в наборі з міткою CIRCLE. Решта вісім штук знаходяться поза трьома сетами. Всі 24 штуки повинні бути враховані.
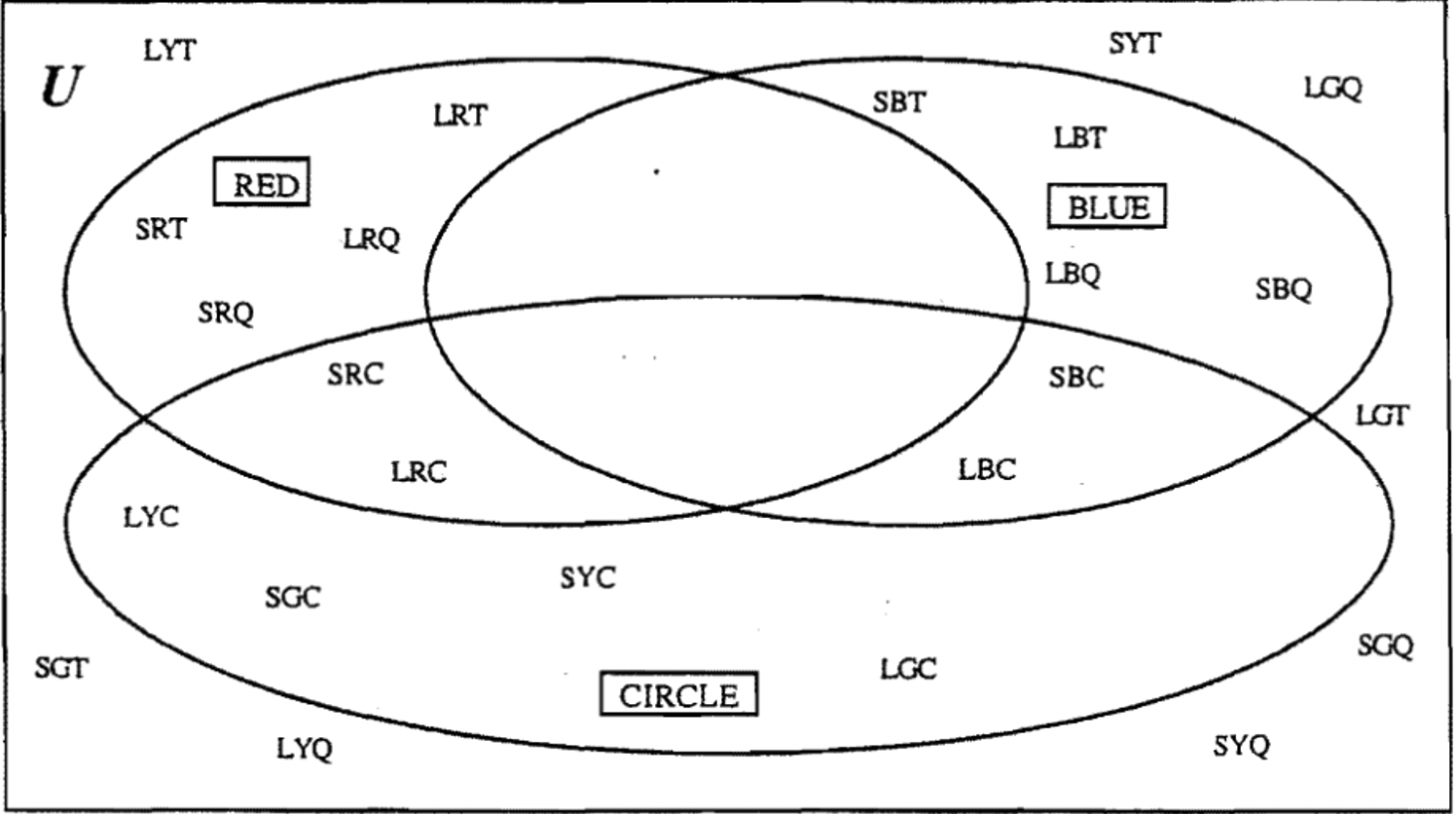
Є момент, який я хочу сказати про креслення діаграм Венна. Набори, які ви малюєте на даній діаграмі Венна, не повинні бути колами, і вони також не повинні бути однакового розміру. Вам просто потрібно обкласти деякий простір. У попередній проблемі ви, можливо, помітили, що я розтягнув набори. Я зробив це, щоб було менш людно, щоб заповнити розміщення A-блоків. Нижче наведено три діаграми Венна, кожна з яких містить три набори. Хоча вони нетрадиційні, вони законні і працюють нормально. Просто зазвичай зручно зробити один шаблон і приклеїти його для однорідності.
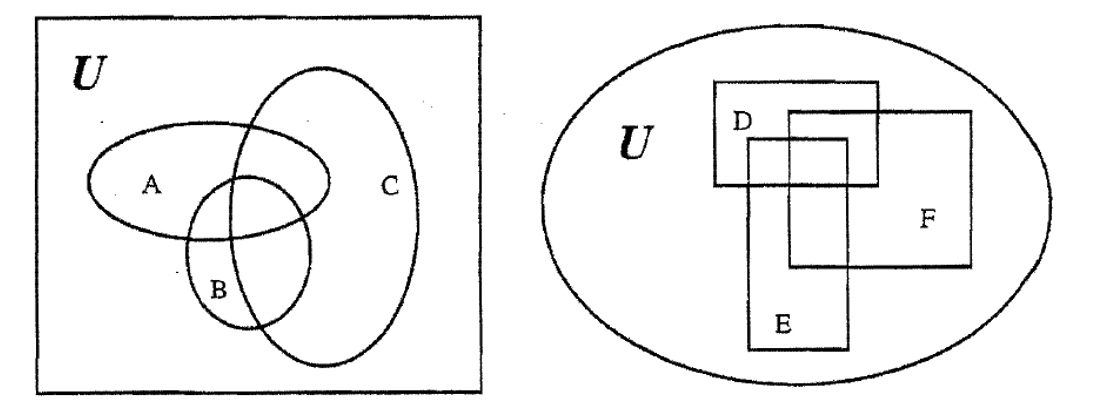
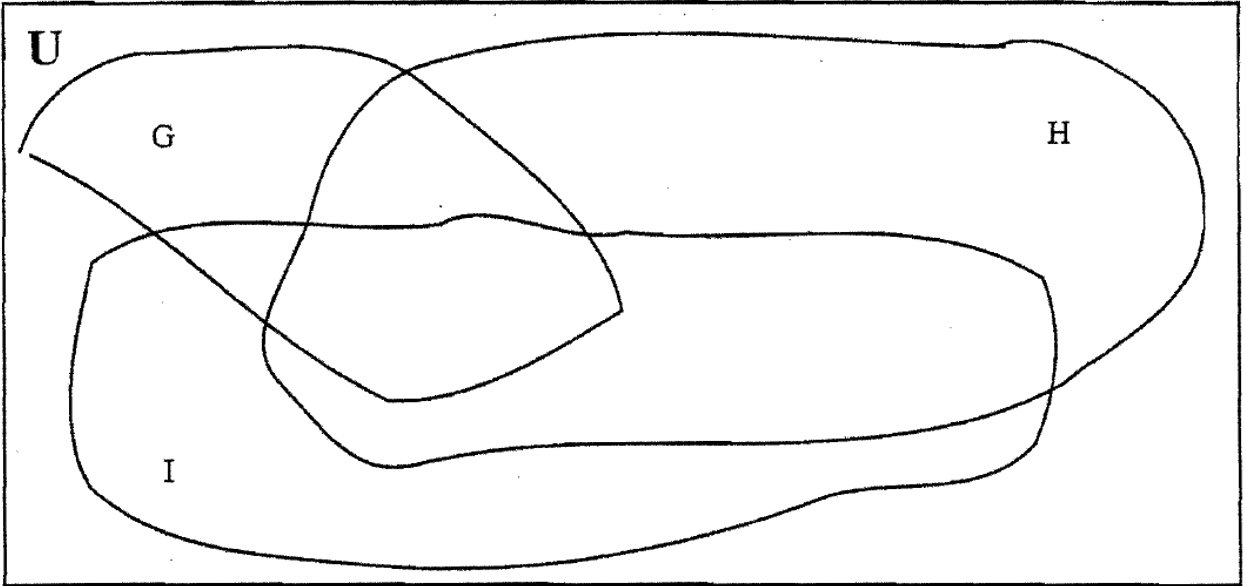
У наступних кількох вправах я розтягнув набори для вас, щоб заповнити скорочення для розміщення A-блоків буде менш переповненим.
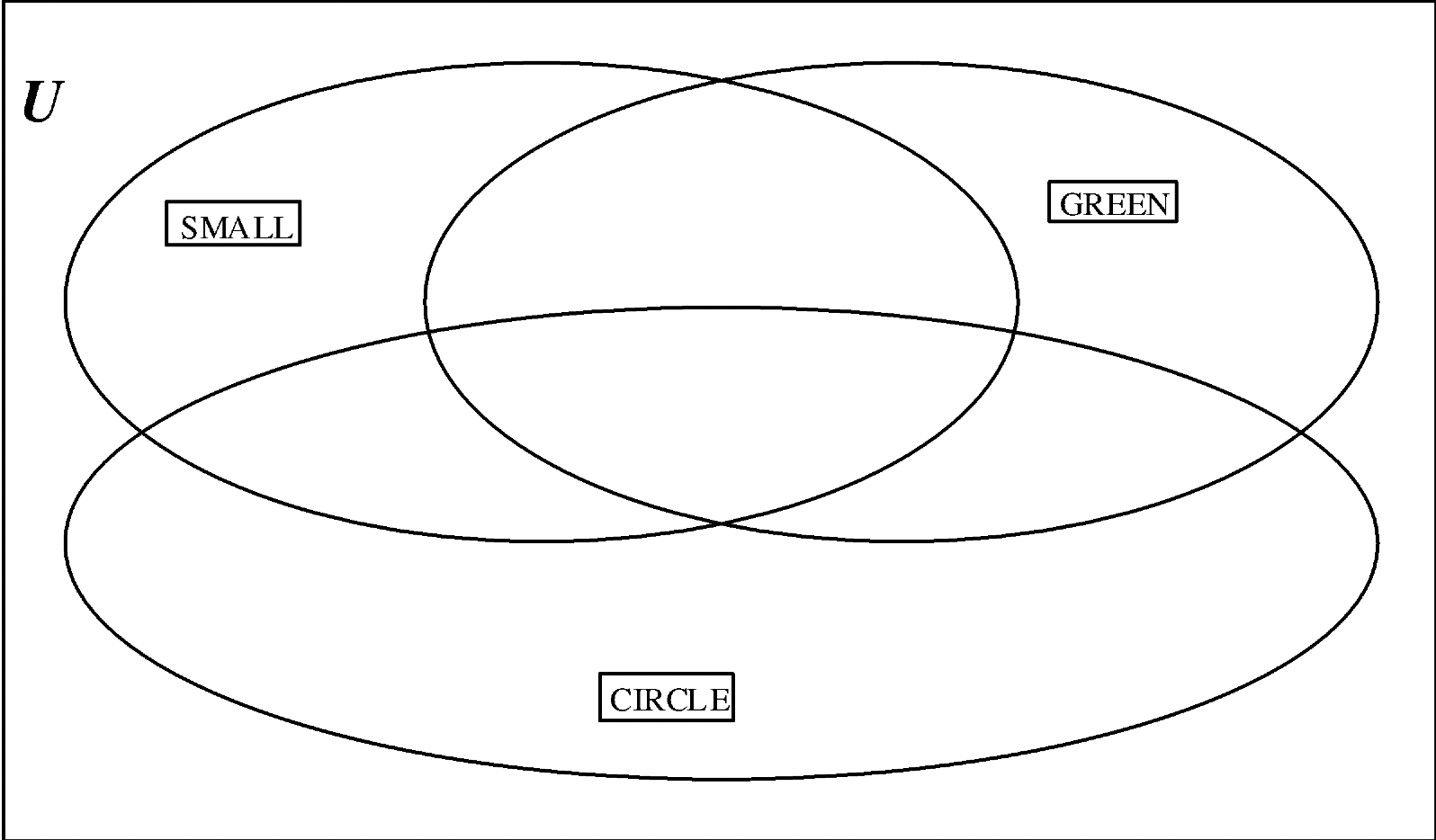
Повторіть вправу #1 на кожній з наступних кількох діаграм Венна, але використовуйте три карти міток значень, показані для трьох наборів. По-перше, використовуйте A-blocks, щоб розмістити кожен елемент у потрібній області на плакаті. Переконайтеся, що ви розміщуєте всі 24 штуки десь у діаграмі Венна (є вісім різних областей, і кожна частина належить рівно до однієї з цих восьми областей). Перевірте свою роботу, розглядаючи кожен набір індивідуально. Після того, як ви відчуєте впевненість, що всі частини розміщені в правильному регіоні, перевірте рішення проти рішення, показаного в модулі рішення. Потім на кожній діаграмі Венна, зображеній на сторінці, напишіть, де ви розмістили фрагменти — використовуйте три літерні скорочення або зображення зображення. Ви повинні бути впевнені, що з огляду на будь-який конкретний блок A, ви можете розмістити його в правильному регіоні.
a. значення: МАЛИЙ (S), ЗЕЛЕНИЙ (G), КОЛО (C)
b Значення: ЧЕРВОНИЙ (R), ЖОВТИЙ (Y), ТРИКУТНИК (T)
c Значення: КВАДРАТ (Q), КОЛО (C), ТРИКУТНИК (T)

d Значення: СИНІЙ (B), ЧЕРВОНИЙ (R), ЗЕЛЕНИЙ (G)

e Складіть нову власну проблему зараз, позначаючи кожен набір значенням з ваших карт міток вартості, як у попередніх вправах. Покажіть рішення місця розташування кожного блоку на діаграмі Венна нижче.
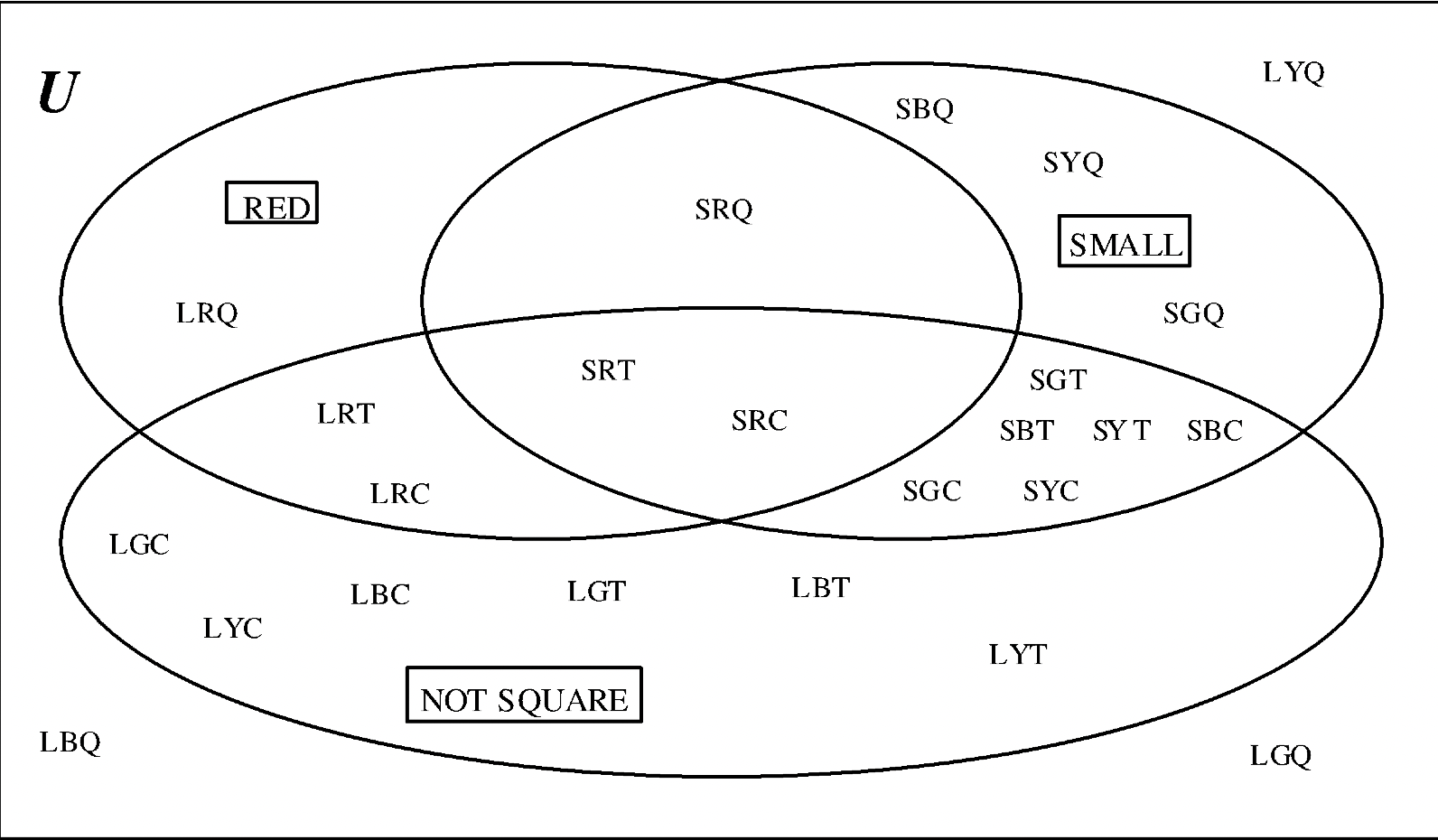
Нижче наведено зображення діаграми Венна, де обрані мітки НЕ КВАДРАТ (\( \bf Q^{c}\)), ЧЕРВОНИЙ (R) та МАЛЕНЬКИЙ (S). Це легко перевірити, тому що я переконуюся, що тільки червоні шматочки і всі червоні шматочки знаходяться в ЧЕРВОНОМУ колі, всі маленькі і не великі шматочки знаходяться в МАЛОМУ колі, і тільки квадрати знаходяться поза НЕ КВАДРАТ коло. Всі 24 штуки припадають на облік.
Використовуйте деякі негативні (НЕ) значення зараз. МАЛИЙ і ВЕЛИКИЙ можна розглядати як позитивні або негативні значення, оскільки МАЛИЙ - це те саме, що НЕ ВЕЛИКИЙ. Позначте кожен набір від'ємним значенням з ваших карт міток вартості. Після розміщення частин на плакаті і перевірки, покажіть рішення про те, де принаймні вісім A-блоків були розміщені на діаграмі Венна нижче.

Деякі картки міток від'ємних значень показані на наступних кількох діаграмах Венна. Використовуйте блоки A - щоб розмістити кожен блок A в правильному регіоні на плакаті. Переконайтеся, що ви враховуєте всі 24 штуки і перевірте свою роботу, дивлячись на кожен набір індивідуально. Потім на кожній показаній діаграмі Венна використовуйте скорочення, щоб позначити, де було розміщено вісім штук.
a. значення: НЕ СИНІЙ (\(\bf B^{c}\)), ВЕЛИКИЙ (L), НЕ ЖОВТИЙ (\(\bf Y^{c}\))
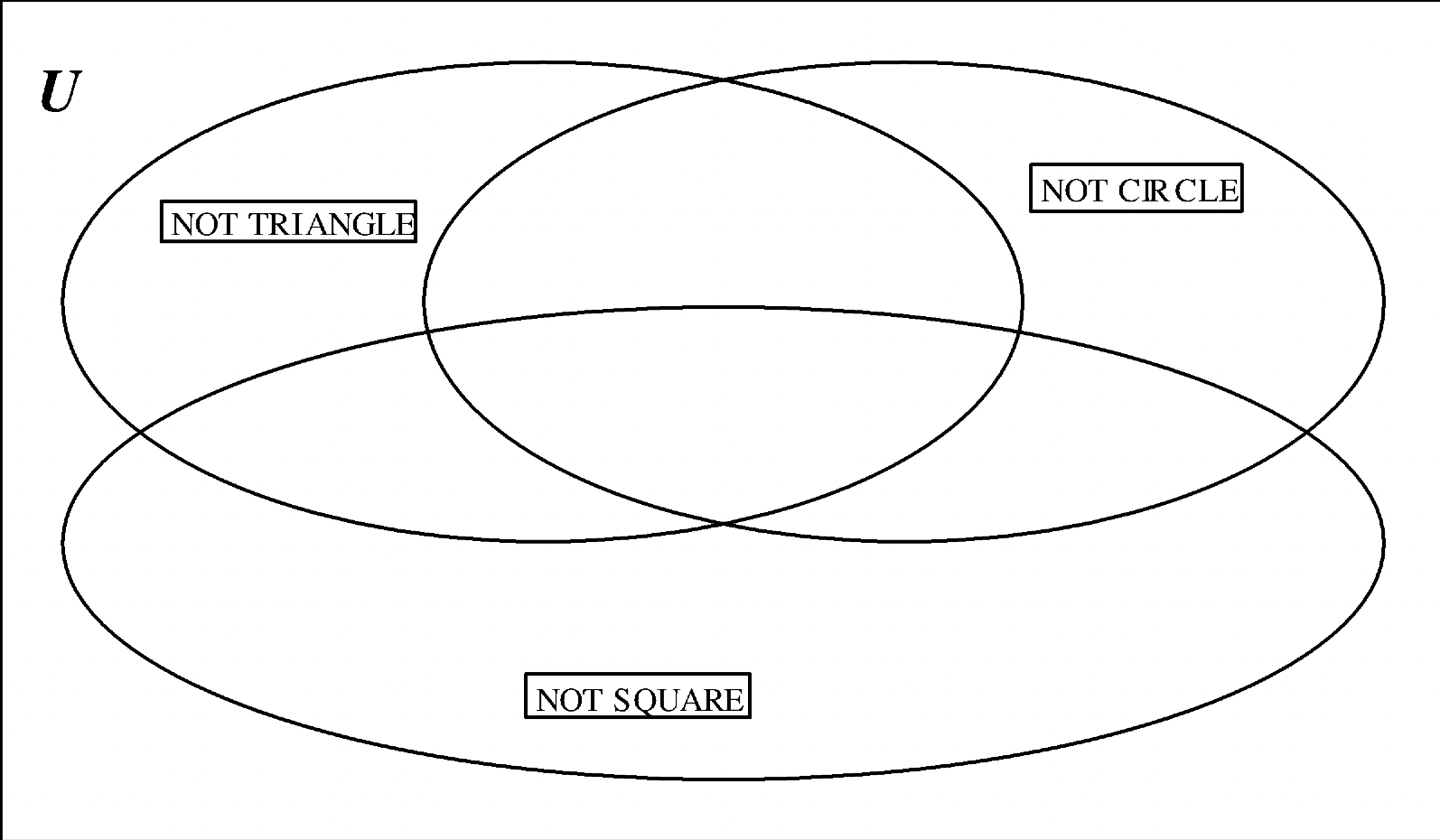
b Значення: НЕ ТРИКУТНИК (\(\bf \bar{T}\)), НЕ КОЛО (\(\bf \bar{C}\)), НЕ КВАДРАТ (\(\bf \bar{Q}\))
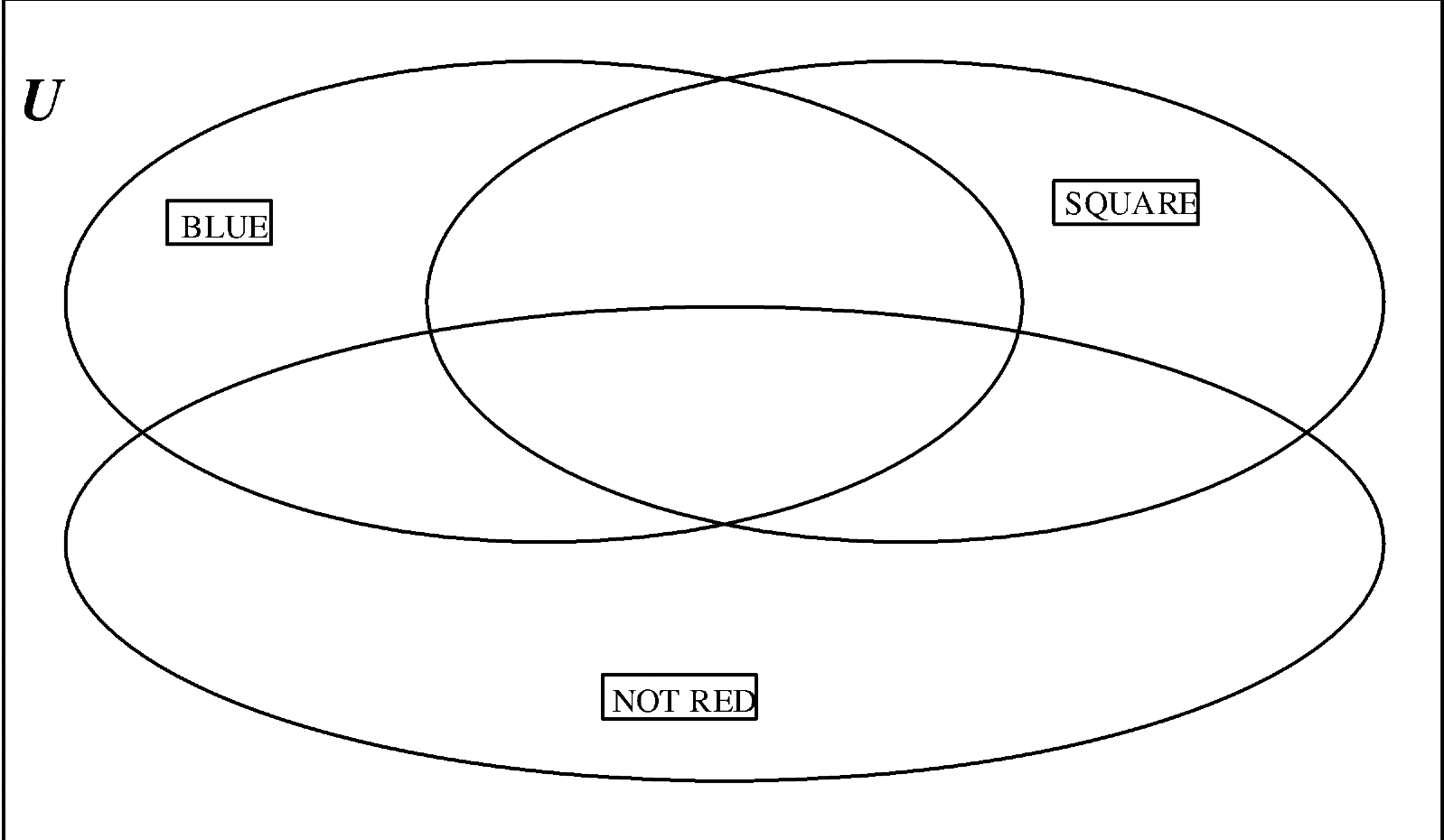
c Значення: СИНІЙ (B), КВАДРАТ (Q), НЕ ЧЕРВОНИЙ (\(\bf R^{c}\))
Назвіть деякі комбінації міток значень, які не залишають шматочків поза трьома наборами.
Назвіть деякі комбінації, які залишають рівно один шматок поза трьома сетами. [Підказка 1: Виберіть шматок, який ви хочете залишитися поза увагою. Підказка 2: Використовуйте деякі не мітки.]
Запишіть деякі комбінації, які залишають найбільшу кількість штук поза сетами. Як ви думаєте, яка найбільша кількість штук, які можна залишити поза трьома колами?
Візьміть одну з ваших порожніх карток етикетки вартості і на ній напишіть\(\bf B \cup Q\) (для СОЮЗУ СИНІХ і КВАДРАТНИХ). Візьміть етикетки картки НЕ СИНІЙ (\(\bf B^{c}\)) і НЕ КВАДРАТ (\(\bf Q^{c}\)) зі свого набору. На плакаті нанесіть кожну етикетку на одному з наборів. Помістіть кожен блок A в правильному регіоні.
a На діаграмі Венна нижче покажіть, де ви розмістили кожен блок A — Block.
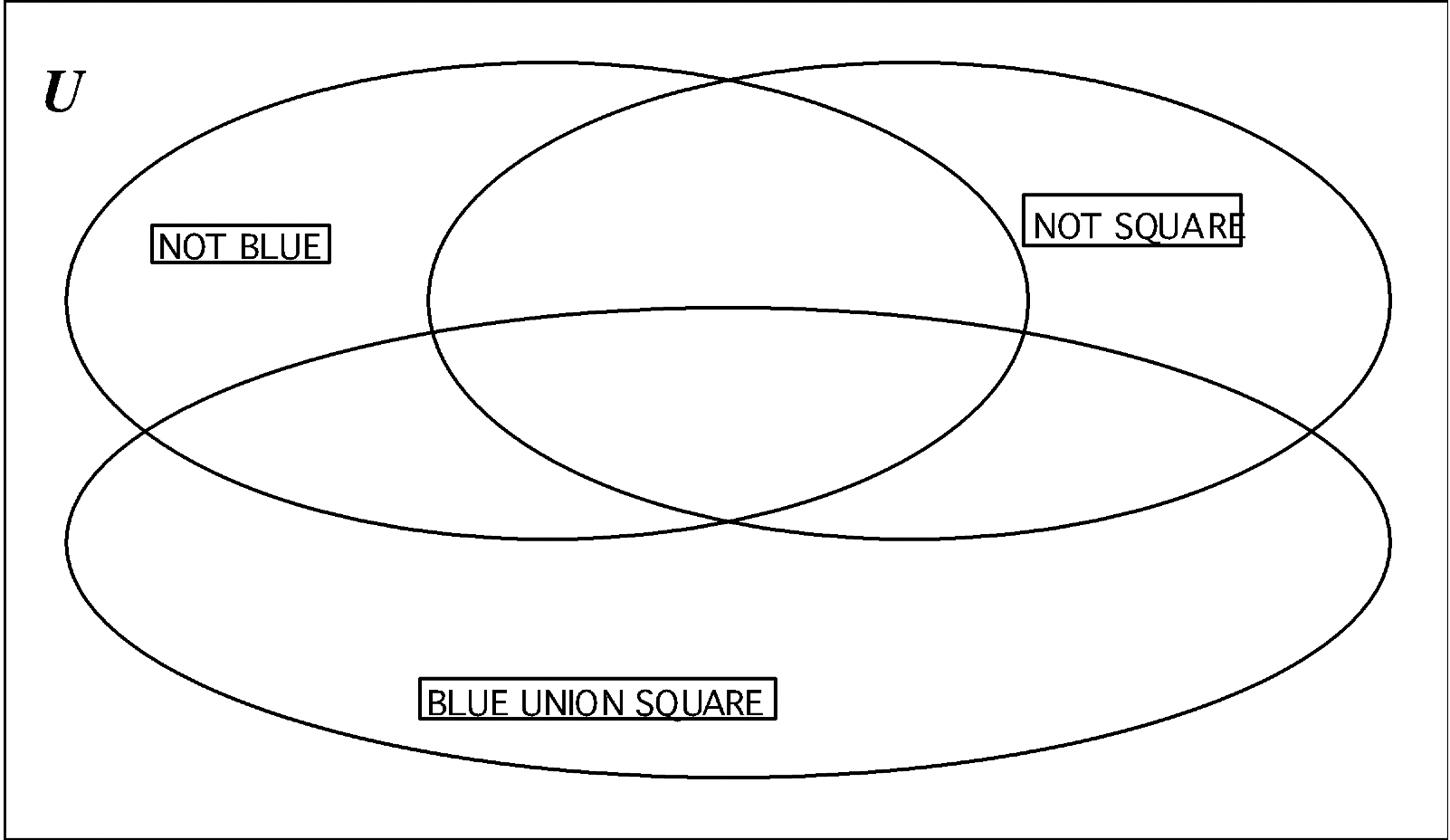
б. подивіться на набір БЛАКИТНИЙ СОЮЗНИЙ КВАДРАТ (B\(\cup\) Q). Подивіться на всі частини поза набором B\(\cup\) Q, щоб ви могли перерахувати елементи в\(\bf (B \cup Q)^{c}\): ____
с. подивіться на перетин НЕ СИНЬОГО і НЕ КВАДРАТНОГО\(\bf B \cap Q^{c}\), і перерахуйте його елементи: ____
d Що ви помічаєте щодо елементів, перерахованих у частині b та частині c вище? ____
е. Напишіть рівняння з того, що ви помітили. ____
Зробіть етикетку картки НЕ ЧЕРВОНИЙ СОЮЗ КОЛО (\(\bf R^{c} \cup C\)) і візьміть ярлики RED (R) і НЕ КОЛО (\(\bf C^{c}\)) зі свого набору.
a. слідуючи вказівкам вправи 8 з цими трьома новими мітками, покажіть, де ви розмістили кожен блок A - на діаграмі Венна нижче.
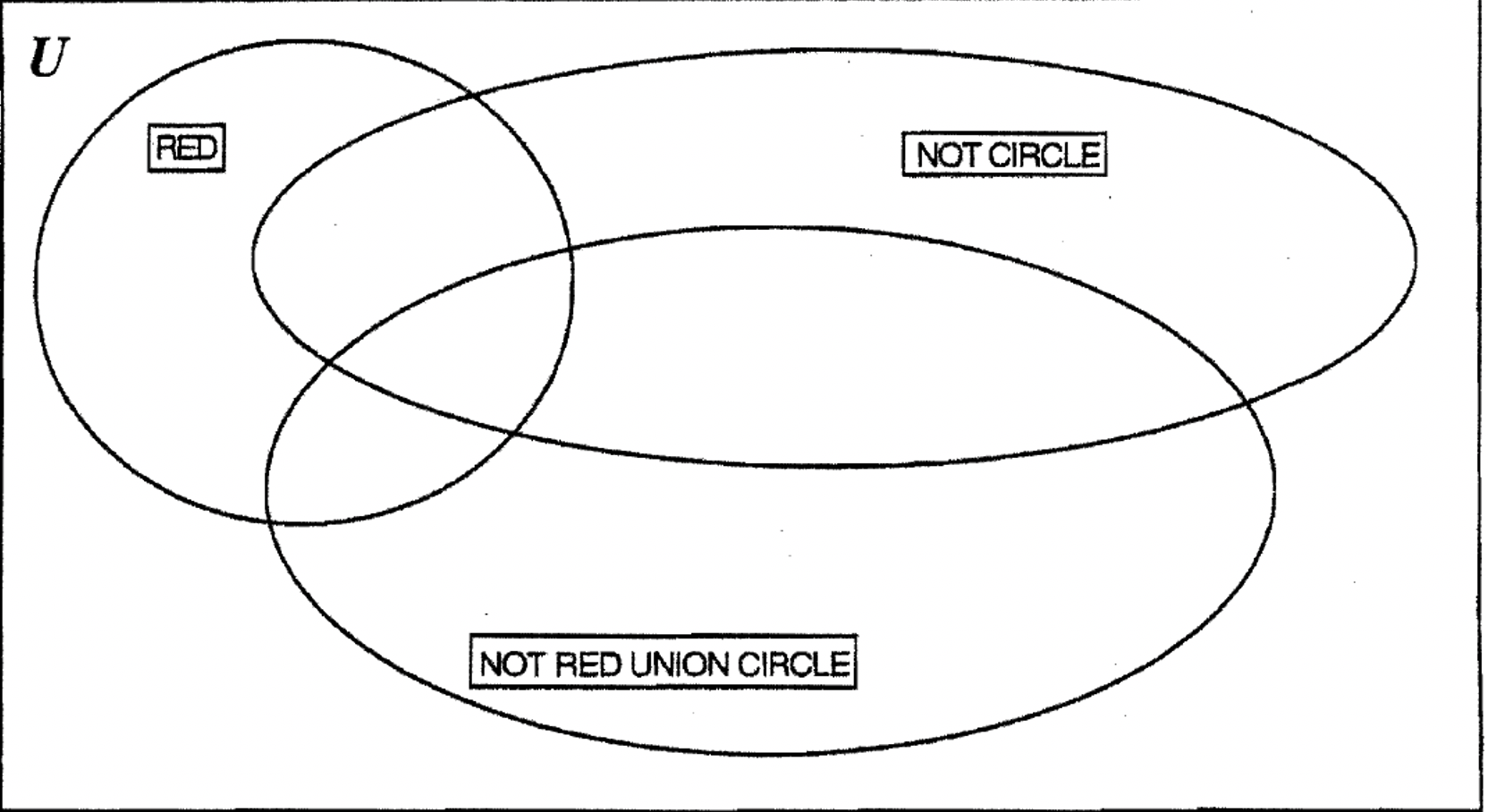
б. подивіться на набір НЕ ЧЕРВОНИЙ СОЮЗ КОЛО (\(\bf R^{c} \cup C\)). Подивіться на всі частини поза набором,\(\bf R^{c} \cup C\) щоб ви могли перерахувати елементи в\(\bf (R^{c} \cup C)^{c}\): ____
c Подивіться на перетин ЧЕРВОНОГО і НЕ КРУГА (\(\bf R \cap C^{c}\)) і перерахуйте його елементи: ____
d Що ви помічаєте щодо елементів, перерахованих у частині b та частині c вище? ____
е. Напишіть рівняння з того, що ви помітили. ____
а Нижче, на діаграмі Венна ліворуч, затіньте вертикальними лініями і затіньте\(\bf B^{c}\) горизонтальними лініями. Подивіться на перекриття обох ліній і затіньте це\(\bf Q^{c}\) перетин на діаграмі Венна праворуч. Тому Венн праворуч представляє\(\bf (B^{c} \cap Q^{c})\).
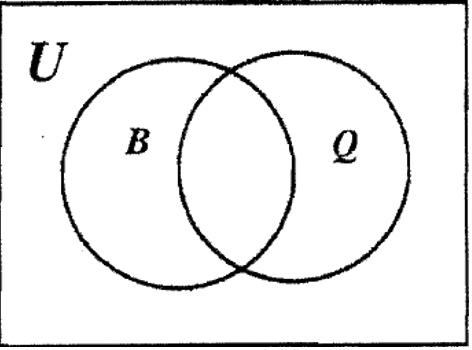 |
 |
б. нижче, на схемі Венна зліва, тінь\(\bf B \cup Q\). На діаграмі Венна праворуч затінюйте все, крім\(\bf B \cup Q\). Потім, Венн праворуч представляє\(\bf (B \cup Q)^{c}\).
 |
 |
c Що ви помічаєте про затінення для\(\bf (B^{c} \cap Q^{c})\) і\(\bf (B \cup Q)^{c}\) (Венни праворуч для a і b)?
d Напишіть рівняння з того, що ви помітили ___
Внизу, на схемі Венна зліва, тінь\(\bf (A \cap B)^{c}\). На діаграмі Венна праворуч розтушовуйте\(\bf A^{c}\) вертикальними лініями і\(\bf B^c\) горизонтальними лініями. Разом загальне затінення праворуч представляє\(\bf A^{c} \cup B^{c}\).
|
а.\(\bf (A \cap B)^{c}\)  |
б.\(\bf A^{c} \cup B^{c}\)  |
c Що ви помічаєте про затінення для\(\bf (A \cap B)^{c}\) і\(\bf A^{c} \cup B^{c}\)?
d Напишіть рівняння з того, що ви помітили ____
Вправи 8, 9, 10 і 11 ілюструють приклади законів ДеМорган.
Один із законів стверджує, що\(\bf (A \cup B)^{c} = A^{c} \cap B^{c}\).
Інший закон ДеМорган стверджує, що\(\bf (A \cap B)^{c} = A^{c} \cup B^{c}\).
Пам'ятайте, що A і B - це просто фіктивні змінні.
В основному, англійською мовою перший із законів ДеМорган (\(\bf (A \cup B)^{c} = A^{c} \cap B^{c}\)) говорить про те, що доповнення об'єднання двох множин дорівнює перетину доповнення кожного множини. Нижче наведено деякі приклади цього закону.
| \(\bf (M \cup N)^{c} = M^{c} \cap N^{c}\) | \(\bf (L^{c} \cup K)^{c} = L \cap K^{c}\) | \(\bf (X^{c} \cup Y^{c})^{c} = X \cap Y\) |
Мені подобається думати про це як про розподіл доповнення по дужках. Для того, щоб прибрати дужки, візьміть доповнення кожного з двох наборів в дужках і змініть об'єднання на перетин.
Другий із законів DeMorgan (\(\bf (A \cap B)^{c} = A^{c} \cup B^{c}\)) говорить, що доповнення перетину двох множин дорівнює об'єднанню доповнення кожного набору. Знову ж таки, це як розподіл доповнення по дужках. Але цього разу перетин змінюється на об'єднання, коли дужки видаляються. Ось кілька прикладів цього закону:
| \(\bf (M \cap N)^{c} = M^{c} \cup N^{c}\) | \(\bf (L^{c} \cap K)^{c} = L \cup K^{c}\) | \(\bf (X^{c} \cap Y^{c})^{c} = X \cup Y\) |
Якщо вам надається об'єднання або перетин будь-яких двох множин, ви можете використовувати Закон ДеМорган, щоб написати його як доповнення кількості. Наприклад, якщо хтось попросив вас написати еквівалентну заяву для\(\bf R \cup S^{c}\), ви використовуєте Закони DeMorgan, щоб написати його як\(\bf (R^{c} \cap S)^{c}\). Зверніть увагу, як це робиться: Щоб отримати дужки з доповненням поза ним, коли немає нічого для початку, як в\(\bf R \cup S^{c}\), почніть з того, щоб поставити дужки з доповненням і розмістити щось всередині, як це:\(\bf R \cup S^{c}\) =\(( \ )^{c}\). Щоб розібратися, що йде всередині, змініть три оригінальні частини на їх «протилежності». Від R до\(R^{c}\), від\(\cup\) до\(\cap\), і від\(S^{c}\) до S. Це дає використання\(\bf R \cup S^{c}\) =\(\bf (R^{c} \cap S)^{c}\). Вам доведеться використовувати цю техніку для 12b, d і f.
Використовуйте закони DeMorgan, щоб написати еквівалентний вираз для кожного твердження нижче.
| \(\bf (R^{c} \cap S^c)^{c}\) | \(\bf M \cap N\) |
| \(\bf (F \cup G^{c})^{c}\) | \(\bf H^{c} \cup I\) |
| \(\bf (P^{c} \cap Q)^{c}\) | \(\bf S \cap T^{c}\) |
Складіть два власних еквівалентних твердження (як у вправі 12), щоб продемонструвати закон ДеМорган.
| а. | б. |
Настав час продемонструвати закони ДеМорган ще одним способом. Повернувшись у вправу Set 1, вправу 13, ви працювали над проблемами, де ми дозволили U = {1, 2, 3, 4, 5, 6, 7, 8, 9}, і ми визначили ці підмножини U: A = {1, 2, 3, 4, 5} B = {2, 4, 6, 8} C = {3, 5, 7}. Ми будемо використовувати ці визначені набори, щоб обчислити наступне і, отже, перевірити закони DeMorgan:
Приклад
Покажіть, що =\(\bf (A \cap B)^{c} = A^{c} \cup B^{c}\).
Рішення
Щоб показати, що дві сторони рівні, спочатку спростіть ліву сторону, обчисливши перетин A і B, (перерахувавши елементи кожної, а потім перерахувавши елементи в перетині). Потім візьміть доповнення цього набору.
\(\bf (A \cap B)^{c} = (\{1, 2, 3, 4, 5\} \cap \{2, 4, 6, 8\})^{c} = (\{2,4\})^c = \{1, 3, 5, 6, 7, 8, 9\}\)
По-друге, спростіть праву сторону, обчисливши доповнення A, а також доповнення B, а потім візьміть об'єднання цих двох множин.
\(\bf A^c \cup B^{c} = (\{1, 2, 3, 4, 5\})^{c} \cup (\{2, 4, 6, 8\})^{c} = \{6, 7, 8, 9\} \cup \{1, 3, 5, 7, 9\} = \{1, 3, 5, 6, 7, 8, 9\}\)
Так як\(\bf (A \cap B)^{c}\) і\(\bf A^c \cup B^{c}\) мають точно такі ж елементи, вони рівні.
Тому\(\bf (A \cap B)^{c} = A^{c} \cup B^{c}\)
Нехай U = {1, 2, 3, 4, 5, 6, 7, 8, 9} і ці визначені підмножини:
| A = {1, 2, 3, 4, 5} | B = {2, 4, 6, 8} | C = {3, 5, 7} |
Перевірте наступне. Показати всі кроки, як зроблено в наведеному вище прикладі. Викладіть остаточний висновок словами.
a. показати, що\(\bf (A \cup B)^{c} = A^{c} \cap B^{c}\)
б. показати, що\(\bf (A \cap C)^{c} = A^{c} \cup C^{c}\)
c. показати, що\(\bf (B^{c} \cup C)^{c} = B \cap C^{c}\)
Ви бачили, як закони ДеМорган продемонстрували багато в чому. Думаєте, ви їх запам'ятаєте? Було кілька вправ, які ви зробили в наборі вправ 2, демонструючи ці закони. Зараз настав час озирнутися назад на ці пари вправ на діаграму Венна, які ви затінювали в наборі вправ 2 # 25 і 28, 26 & 29, 44 & 45 і 50 & 52.
Настав час продемонструвати ще дві цікаві властивості про множини.
a Ми будемо затінювати діаграми Венна, що представляють\(\bf A \cap (B \cup C)\) і\(\bf (A \cap B) \cup (A \cap C)\). На лівій діаграмі Венна затінюйте A горизонтальними лініями\(\bf B \cup C\) та вертикальними лініями. Потім відбувається перекриття\(\bf A \cap (B \cup C)\). Затінюйте лише нахлест на середній діаграмі Венна. Так як\(\bf (A \cap B) \cup (A \cap C)\) це союз, затіньте обидва\(\bf A \cap B\) і\(\bf A \cap C\) на правій діаграмі Венна.
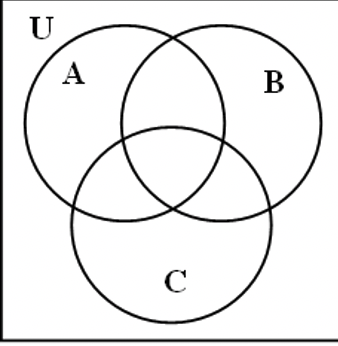 |
 \(\bf A \cap (B \cup C)\) \(\bf A \cap (B \cup C)\) |
 \(\bf (A \cap B) \cup (A \cap C)\) \(\bf (A \cap B) \cup (A \cap C)\) |
b Що ви помічаєте щодо остаточних затінення діаграм Венна для\(\bf A \cap (B \cup C)\) і\(\bf (A \cap B) \cup (A \cap C)\)?
Як і у вправі 14, нехай U = {1, 2, 3, 4, 5, 6, 7, 8, 9}, і визначити ці підмножини U:
| A = {1, 2, 3, 4, 5} | B = {2, 4, 6, 8} | C = {3, 5, 7} |
Обчисліть наступне:
с.\(\bf A \cap (B \cup C)\) = ____
д.\(\bf (A \cap B) \cup (A \cap C)\) = ____
е Що ви помічаєте про відповіді на c і d? ____
a Ми будемо затінювати діаграми Венна, що представляють\(\bf (A \cup B) \cap (A \cup C)\) і\(\bf A \cup (B \cap C)\). На лівій схемі Венна\(\bf A \cup B\) затінюйте горизонтальними лініями і\(\bf A \cup C\) вертикальними лініями. Потім відбувається перекриття\(\bf (A \cup B) \cap (A \cup C)\). Затінюйте лише нахлест на середній діаграмі Венна. Оскільки\(\bf A \cup (B \cap C)\) це союз, затіньте як A, так і\(\bf B \cap C\) на правій діаграмі Венна.
 |
 \(\bf (A \cup B) \cap (A \cup C)\) \(\bf (A \cup B) \cap (A \cup C)\) |
 \(\bf A \cup (B \cap C)\) \(\bf A \cup (B \cap C)\) |
b Що ви помічаєте щодо остаточних затінення діаграм Венна для\(\bf (A \cup B) \cap (A \cup C)\) і\(\bf A \cup (B \cap C)\)?
Як і у вправі 14, нехай U = {1, 2, 3, 4, 5, 6, 7, 8, 9}, і визначити ці підмножини U:
| A = {1, 2, 3, 4, 5} | B = {2, 4, 6, 8} | C = {3, 5, 7} |
Обчисліть наступне:
с.\(\bf A \cup (B \cap C)\) = ____
д.\(\bf (A \cup B) \cap (A \cup C)\) = ____
е Що ви помічаєте про відповіді на c і d? ____
Вправи 15 і 16 демонструють дві розподільні властивості множин.
Перший розподіляє перетин по союзу:
Для трьох наборів, A, B і C, \(\bf A \cap (B \cup C) = (A \cap B) \cup (A \cap C)\).
Другий розподіляє союз по перетину:
Для трьох наборів, A, B і C, \(\bf A \cup (B \cap C) = (A \cup B) \cap (A \cup C)\).
Нижче наведено кілька прикладів цих властивостей.
\(\bf A^{c} \cup (M^{c} \cap N) = (A^{c} \cup M^{c}) \cap (A^{c} \cup N)\)
\(\bf (B \cap T^{c}) \cup (B \cap S) = B \cap (T^{c} \cup S)\)
Використовуйте розподільні властивості множин, щоб переписати кожне з наведених нижче параметрів (не викидайте доповненнями):
а.\(\bf X \cap (Y \cup Z)\) = ____
б.\(\bf P \cup (Q^{c} \cap R)\) = _____
с.\(\bf (K^{c} \cap L) \cup (K^{c} \cap M)\) = ______
д.\(\bf (D \cup E^{c}) \cap (D \cup F)\) = _____
Вправи 53 і 54 в наборі вправ 2 продемонстрували один з розподільних законів. Зараз настав час, щоб озирнутися на них.
