Skip to main content
LibreTexts - Ukrayinska

2.8: Граф Борда

  1. Last updated
  2. Save as PDF
  • Page ID
    66190

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Борда граф - ще один метод голосування, названий на честь Жан-Шарля де Борда, який розробив систему в 1770 році.

    Борда Граф

    У цьому методі бали призначаються кандидатам на основі їх рейтингу; 1 бал за останній вибір, 2 бали за другий вибір і так далі. Значення балів за всі бюлетені підсумовуються, а кандидат з найбільшою кількістю балів є переможцем.

    Приклад 8

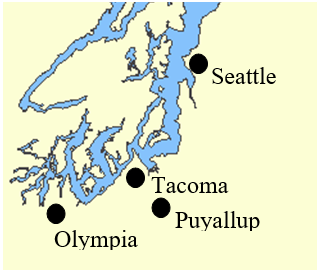    На мапі показано розташування міст 4: Олімпія, Такома, Пуйаллап і СіетлГрупа математиків збираються разом на конференцію. Члени приїжджають з чотирьох міст: Сіетл, Такома, Пуйаллап та Олімпія. Їх приблизні місця розташування на карті показані праворуч.

    Голосами за те, де провести конференцію, були:

    \ (\ почати {масив} {|l|l|l|l|l|}
    \ hline & 51 & 25 & 10\\
    \ hline 1^ {\ текст {st}}\ текст {вибір} &\ текст {Сіетл} &\ текст {Такома} &\ текст {Пуяллап} &\ текст {Олімпія}
    \\ hline 2^ {Текст {nd}\ текст {вибір} &\ текст { Такома} &\ текст {Пуйаллап} &\ текст {Такома} &\ текст {Такома}\
    \ hline 3^ {\ текст {rd}}\ текст {вибір} &\ текст {Олімпія} &\ текст {Олімпія} &\ текст {Олімпія} &\ текст {Пуяллап}
    \\ hline 4^ {текст {th}}\ текст {вибір} &\ текст { Додати} &\ text {Сіетл} &\ text {Сіетл} &\ text {Сіетл}
    \\ hline
    \ end {масив}\)

    Рішення

    У кожному з 51 бюлетенів рейтингу Сіетл першим, Пуйаллап отримає 1 бал, Олімпія 2 бали, Такома 3 бали та Сіетл 4 бали. Множення балів за один голос на кількість голосів дозволяє нам розрахувати нараховані бали:

    \ (\ почати {масив} {|l|l|l|l|l|}
    \ hline & 51 & 25 & 10 & 14\
    \ hline 1^ {\ текст {st вибір}} &\ текст {Сіетл} &\ текст {Такома} &\ текст {Пуяллап} &\ текст {Олімпія}\\
    4\ текст {точки} & 4\ cdot 51=204 & 4\ крапка 25 = 100 & амп; 4\ cdot 10 = 40 & 4\ cdot 14=56
    \\ hline 2^ {\ текст {і вибір}} &\ текст {Такома} &\ текст {Пуяллап} &\ текст {Такома}\\ текст {Такома}\
    3\ текст {точки} & 3\ cdot 51 = 153 & 3\ cdot 25=75 & 3\ cdot 10=30 & 3\ крапка 14 = 42\\
    \ hline 3^ {\ текст {rd}}\ текст {вибір} &\ текст {Олімпія} &\ текст {Олімпія} &\ текст {Олімпія} &\ текст {Пуяллап}\\
    2\ текст {точки} & 2\ cdot 51 = 102 & 2\ cdot 25 = 50 & 2\ cdot 10 = 20 & 2\ cdot 14 = 28
    \\\ hline ^ {\ текст {th}}\ текст { вибір} &\ текст {Пуяллап} &\ текст {Сіетл} &\ текст {Сіетл} &\ текст {Сіетл}\
    1\ текст {точка} & 1\ cdot 51 & 1\ cdot 25 = 25 & 1\ cdot 10 = 10 & 1\ cdot 14=14\
    \ hline
    \ кінець {масив}\)

    Складання балів:

    • Сіетл:\(204 + 25 + 10 + 14 = 253\) окуляри
    • Такома:\(153 + 100 + 30 + 42 = 325\) бали
    • Пуйаллап:\(51 + 75 + 40 + 28 = 194\) бали
    • Олімпія:\(102 + 50 + 20 + 56 = 228\) бали

    За методом Борда Граф, Такома є переможцем цього голосування.

    Спробуйте зараз 4

    Розглянемо ще раз вибори від Спробуйте зараз 1. Знайдіть переможця за допомогою графа Борда. Оскільки у нас є деякі неповні виборчі бюлетені, для простоти, дайте кожному неоціненому кандидату 1 бал, бали, які вони зазвичай отримують за останнє місце.

    \ (\ почати {масив} {|l|l|l|l|l|l|l|l|l|}
    \ лінія & 44 & 14 & 20 & 20 & 22 & 80 & 39
    \\\ рядок 1^ {\ текст {st}}\ текст {вибір} &\ математика {G} &\ математика {G} &\ mathrm {G} &\ mathrm {M} &\ математика {M} &\ математика {B} &\ математика {B}\\
    \ hline 2^ {\ текст {nd}}\ текст {вибір} &\ математика {M} &\ математика {B} &\ математика {G} &\ математика {B} &\ mathrm {M} &\\
    \ рядок 3^ {текст {rd}}\ текст {вибір} &\ mathrm {B} &\ mathrm {M} &\ математика {B} &\ математика {G} &\ mathrm {G} &\\
    \ hline
    \ end {масив}\)

    Відповідь

    Використання Borda Count:

    Даємо 1 бал за 3-е місце, 2 бали за 2-е місце і 3 бали за 1-е місце.

    \ (\ почати {масив} {|l|l|l|l|l|l|l|l|l|}
    \ лінія & 44 & 14 & 20 & 20 & 22 & 80 & 39
    \\\ рядок 1^ {\ текст {st}}\ текст {вибір} &\ математика {G} &\ математика {G} &\ mathrm {G} &\ mathrm {M} &\ математика {M} &\ математика {B} &\ математика {B}\\
    & 132\ математика {pt} & 42\ математика {pt} & 60\ математика {pt} & 210\ математика {pt} & 66\ математика {pt} & 240\ mathrm {pt} & 117\ mathrm {pt}
    \\ рядок 2^ {текст {nd}}\ текст {вибір} &\ mathrm {M} &\ mathrm m {B} &\ математика {G} &\ mathrm {B} &\ математика {M} &\\
    & 88\ математика {pt} & 28\ математика {pt} & & 140\ математика {pt} & 44\ математика {pt} & 160\ mathrm {pt} &
    \\\ рядок 3^ {текст {rd}}\ текст {вибір} &\ математика {B} &\ mathrm {M} therm {M} 20\ математика {pt} &\ математика {B} &\ математика {G} &\ математика {G} &\ математика {M} 39\ математика {pt}\\
    & 44\ математика {pt} & 14\ математика {pt} &\ mathrm {B} 20\ mathrm {pt} & 70\ mathrm {pt} & 22\ mathrm {pt}\ mathrm {G} 39\ mathrm {pt}\
    \ рядок
    \ кінець {масив}\)

    Г:\(132+42+60+140+22+80+39 = 515\) оч

    М:\(88+14+20+210+66+160+39 = 597\) оч

    Б:\(44+28+20+70+44+240+117 = 563\) оч

    Маккарті (М) стане переможцем, використовуючи граф Борда.