11.3: Приведена вартість ануїтетів
- Page ID
- 66820
Ви коли-небудь помічали, що ціни на дорогі продукти взагалі не рекламуються? Натомість компанії, які продають ці продукти з високим квитком, рекламують суми оплати ануїтету, а не фактичну ціну наклейки. Насправді, розміщення фактичної ціни на ці товари в оголошеннях зазвичай вимагає збільшувального скла. Наприклад, Mitsubishi Outlander нещодавно рекламувався всього за 193 долари щотижня. Це не звучить так погано, і, можливо, у вас може виникнути спокуса відправитися вниз до автосалону, щоб купити один з цих транспортних засобів. Однак дрібний шрифт вказує на те, що вам потрібно зробити 182 платежі, які потім складають майже 32 000 доларів. Чому транспортний засіб рекламується саме таким чином? Чисельно, $193 звучить набагато краще, ніж $32,000!
У бізнесі, незалежно від того, налаштовуєте ви споживачів з планами платежів або купівлі-продажу кредитних договорів, вам потрібно розрахувати поточні значення. Як споживач, ви стикаєтеся з розрахунками теперішньої вартості різними способами:
- Як взяти рекламовані суми платежів і конвертувати їх у фактичну ціну, яку ви повинні заплатити.
- Досягнення фінансових цілей шляхом планування вашого RRSP, що вимагає знати, скільки грошей вам потрібно на старті.
У цьому розділі розробляються формули поточної вартості як для звичайних ануїтетів, так і для рентних. Як і майбутні розрахунки вартості, ці формули вміщують як прості, так і загальні ануїтети за потребою. З інвестицій ми потім продовжимо розрахунки ануїтету на кредити, а також.
Звичайні ануїтети та ануїтети
Приведена вартість будь-якого ануїтету дорівнює сумі всіх нинішніх значень всіх ануїтетних платежів при їх перенесенні на початок першого інтервалу виплат. Наприклад, припустимо, що ви будете отримувати $1,000 щорічних платежів наприкінці кожного інтервалу платежів протягом наступних трьох років від інвестиційного заробітку 10%, що збільшується щорічно. Скільки грошей має бути в ануїтет на початку, щоб це сталося? В цьому випадку у вас звичайна проста ануїтет. На малюнку нижче ілюструється основна концепція часової вартості грошей і показані розрахунки при переміщенні всіх платежів до фокусної дати на початку часової шкали.
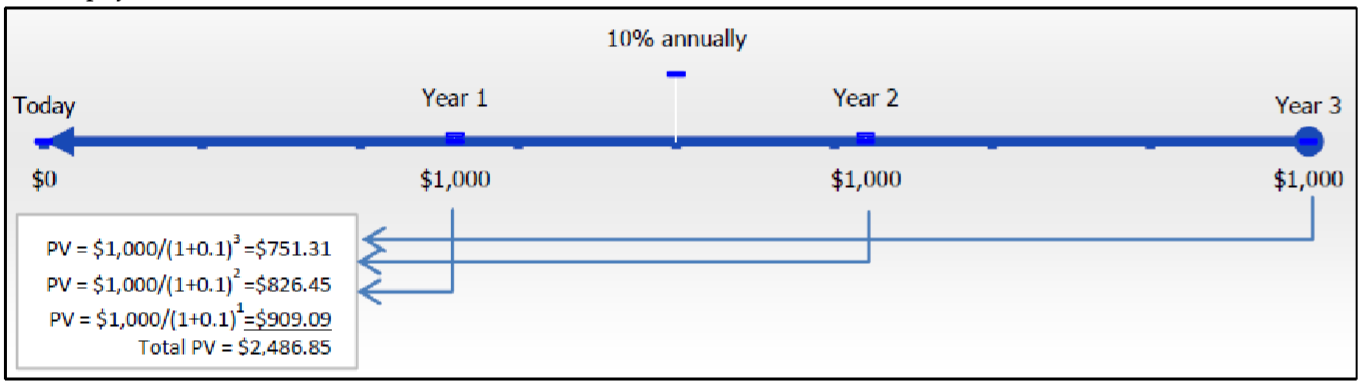
Зверніть увагу, що всі три платежі присутні на вашій фокусній даті, що вимагає інвестицій у розмірі 2,486,85 доларів сьогодні. На відміну від цього, що відбувається з вашою шкалою та розрахунками, якщо ці платежі здійснюються на початку кожного інтервалу платежів? У цьому випадку у вас є проста рента за рахунок. Наступний малюнок ілюструє ваші терміни і розрахунки.
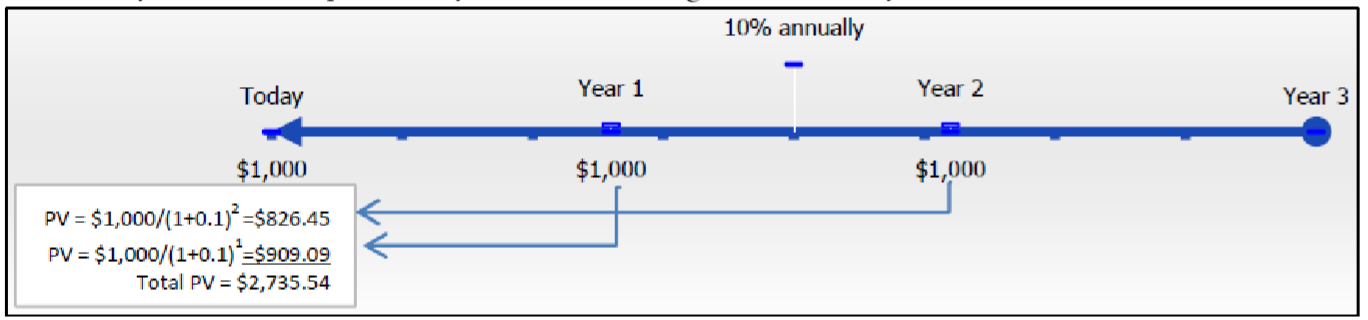
Зверніть увагу, що лише два з трьох платежів повинні бути присутніми, оцінені до вашої фокусної дати, оскільки перший платіж вже на фокусну дату. Загальна сума інвестицій для ануїтету вище на рівні $2,735.54, оскільки перший платіж знімається негайно, тому менший основний капітал заробляє менше відсотків, ніж звичайний ануїтет.
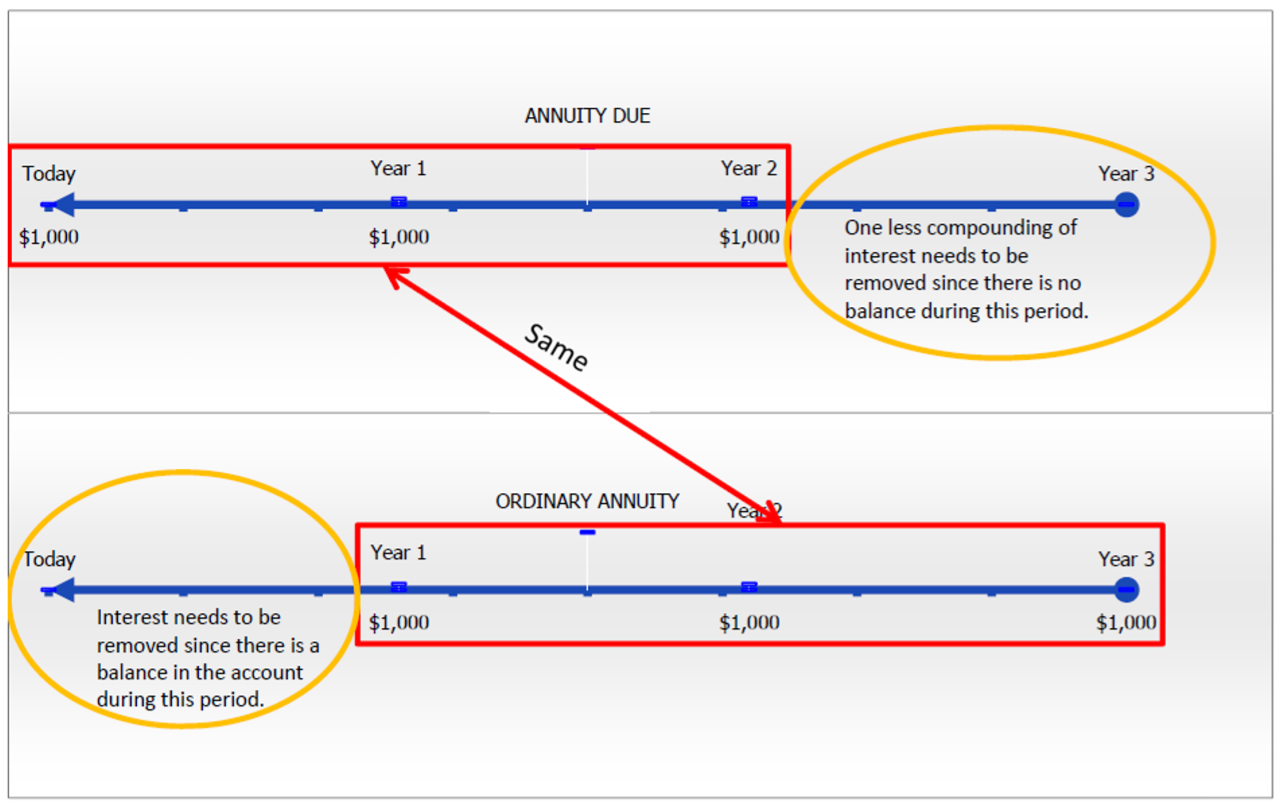
Наступна цифра нижче контрастує два типи ануїтету. Працюючи справа наліво на часовій шкалі, ключова відмінність полягає в тому, що ануїтет через має один менший склад відсотків, щоб видалити. Його перший часовий сегмент (праворуч) містить нульовий баланс, тоді як звичайний ануїтет дійсно містить баланс, який повинен мати відсотки зі знижкою. Зверніть увагу, що якщо ви берете ануїтет до сплати і видалити один додатковий склад відсотків, ви прибудете в $2,735,54 ÷ (1 + 0,1) = $2,486.85, що є поточною вартістю відповідного звичайного ануїтету.
Формула
Як і у випадку з майбутніми розрахунками вартості, обчислення поточних значень шляхом ручного переміщення кожного платежу до його теперішньої вартості є надзвичайно трудомістким, коли є більше кількох платежів. Аналогічним чином ануїтетні формули дозволяють переміщати всі платежі одночасно в єдиному розрахунку. Формули для звичайних ануїтетів і ануїтетів, що належать, представлені разом.
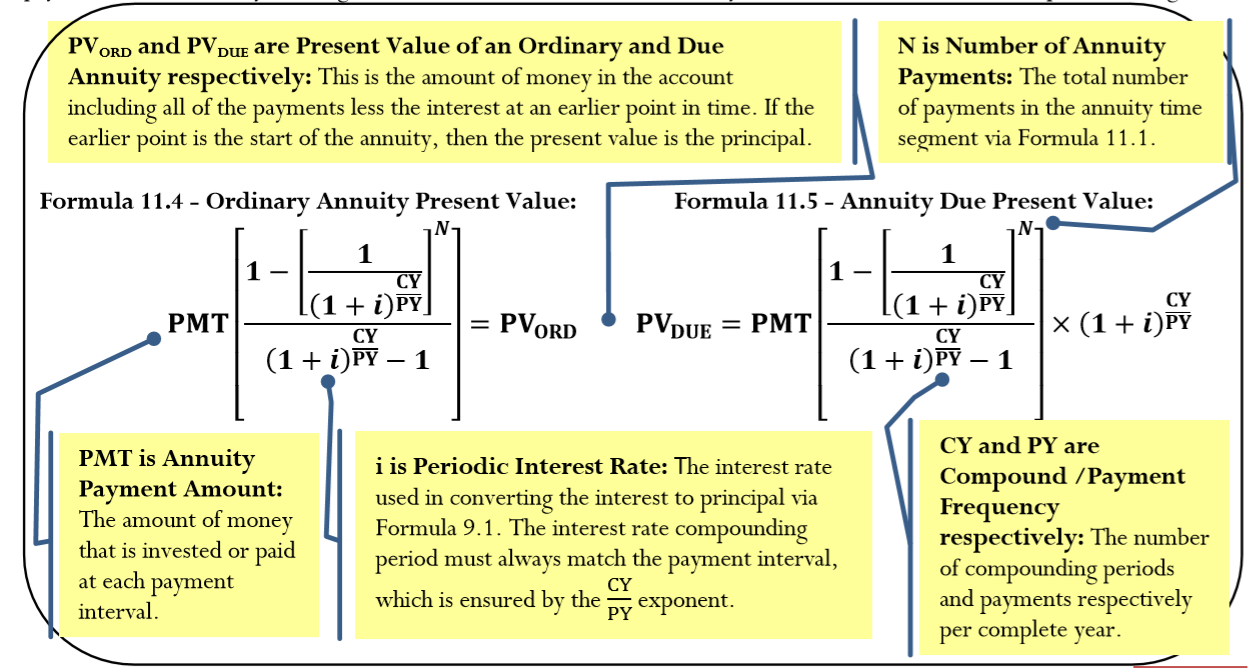
З приводу цих двох формул робляться наступні спостереження:
- Формули адаптуються як до простих, так і до загальних ануїтетів. У випадку простих ануїтетів частота складання вже відповідає частоті виплат, тому вона не вимагає перетворення; чисельно показник\(\dfrac{CY}{PY}\) виробляє частку 1 і видаляє себе з формули. У випадку загальних ануїтетів показник перетворює частоту складання процентної ставки відповідно до частоти виплат.
- Ідентичні за структурою формули майбутніх значень, ці дві формули для теперішнього значення також є складними рівняннями, що включають швидкість, частину та базу. Тут теперішнє значення (\(PV_{ORD}\)або\(PV_{DUE}\)) = порція,\(PMT\) = база, а все інше = ставка. Чисельник виробляє загальне зменшення відсотка ануїтету; знаменник\((1+i)^{\frac{CY}{PY}}-1\), виробляє зміну відсотків з кожним платежем; поділ цих двох відсотків змін створює коефіцієнт, за яким поточна вартість відноситься до самого ануїтетного платежу.\(1-\left[\dfrac{1}{(1+i)^{\frac{CY}{PY}}}\right]^{N}\) Для ілюстрації припустимо, що\(i\)\(N\) = 5%, = 2, і\(CY = PY\) = 1. Підстановка цих чисел у формулу дає наступне:\[\dfrac{1-\left[\dfrac{1}{(1+i)^{\frac{CY}{PY}}}\right]^N}{(1+i)^{\frac{CY}{PY}}-1}=\dfrac{1-\left[\dfrac{1}{(1+.05)^{\frac{1}{1}}}\right]^{2}}{(1+.05)^{\frac{1}{1}}-1}=\dfrac{0.092970}{0.05}=1.859410 \nonumber \] З цих чисел видно, що сума теперішнього значення являє собою зменшення на 9,2970% (чисельник) в цілому. З кожним платежем зменшення становить 5% (знаменник). Таким чином, відношення поточної вартості в цілому до кожного платежу (a\(PMT\)) становить 1.859410. Якщо сума ануїтетного платежу\(PMT\) = $1,000, то значення\(PV_{ORD}=\$ 1,000(1.859410)=\$ 1,859.41\).
- Єдина відмінність від звичайної ануїтету - множення додаткового терміну\((1+i)^{\frac{CY}{PY}}\). Множення призводить до видалення однієї меншої кількості сполук відсотків, ніж звичайна ануїтет.
Як це працює
Виконайте наступні дії, щоб розрахувати поточну вартість будь-якого звичайного ануїтету або ануїтету належної:
Крок 1: Визначте тип ануїтету. Намалюйте часову шкалу, щоб візуалізувати питання.
Крок 2: Визначте змінні, які ви знаєте, включаючи\(FV, IY, CY, PMT, PY\), і Years.
Крок 3: Використовуйте формулу 9.1 для розрахунку\(i\).
Крок 4: Якщо\(FV\) = $0, перейдіть до кроку 5. Якщо є ненульове значення для\(FV\), поводьтеся з ним як до єдиного платежу. Застосовуйте формулу 9.2, щоб визначити,\(N\) оскільки це не розрахунок ануїтету. Перемістіть майбутнє значення на початок часового відрізка за допомогою Формули 9.3, переставляючи для\(PV\).
Крок 5: Використовуйте формулу 11.1 для розрахунку\(N\). Застосовуйте або Формулу 11.4, або Формулу 11.5 на основі типу ануїтету. Якщо ви розрахували поточну вартість на кроці 4, об'єднайте теперішні значення з кроків 4 та 5, щоб отримати загальну поточну вартість.
Важливі примітки
Розрахунок суми відсотків. Якщо вам цікаво дізнатися, скільки відсотків було знято при розрахунку теперішньої величини, адаптуйте Формулу 8.3, де\(I = S – P = FV − PV\). Теперішнє значення (\(PV\)) - це рішення або Формули 11.4, або Формули 11.5. \(FV\)У Формулі 8.3 розширено, щоб включити суму всіх майбутніх грошей, тому вона замінюється на\(N × PMT + FV\). Тому ви переписуєте формулу 8.3 як\(I = (N × PMT + FV) − PV\).
Ваш калькулятор BAII+. Якщо майбутня вартість одного платежу (FV) бере участь у розрахунку поточної вартості, то вам потрібно два розрахунки формули за допомогою Формули 9.3 та або Формули 11.4 або Формули 11.5. Калькулятор виконує обидва ці обчислення одночасно, якщо ви вводите значення відповідно до угоди про знак грошового потоку для обох\(FV\) і\(PMT\).
Для двох рівних інвестиційних ануїтетів, чи буде поточна вартість звичайного ануїтету та ануїтету належної бути однаковою або різною?
- Відповідь
-
Вони будуть різними. Ануїтет за рахунок завжди має більшу теперішню вартість, оскільки вона видаляє одну меншу кількість відсотків, ніж звичайний ануїтет.
Родрігес планує мати річний валовий дохід у розмірі 50,000 доларів наприкінці кожного року, коли він виходить на пенсію у віці 65 років. Він планує спорожнити рахунок до 78 років, що є середньою тривалістю життя для канадського чоловіка. Якщо на рахунку заробляє 5,1% в сукупності щорічно, яка сума коштів повинна бути на рахунку при виході на пенсію?
Рішення
Крок 1:
Платежі знаходяться в кінці інтервалів платежів, а період складання та інтервали платежів однакові. Це, отже, звичайний простий ануїтет. Обчисліть його значення на початку, яке є його теперішньою вартістю, або\(PV_{ORD}\).
Що ви вже знаєте
Крок 1 (продовження):
Нижче відображається шкала часу для облікового запису клієнта.

Крок 2:
\(FV\)= 0$,\(IY\) = 5,1%,\(CY\) = 1,\(PMT\) = 50 000$,\(PY\) = 1, років = 13
Як ви туди потрапите
Крок 3:
Застосувати формулу 9.1.
Крок 4:
Оскільки\(FV\) = $0, пропустіть цей крок.
Крок 5:
Застосовуємо Формулу 11.4 і Формулу 11.5.
Виконувати
Крок 3:
\(i=5.1 \% \div 1=5.1 \%\)
Крок 5:
\(N=1 \times 13=13\)платежі
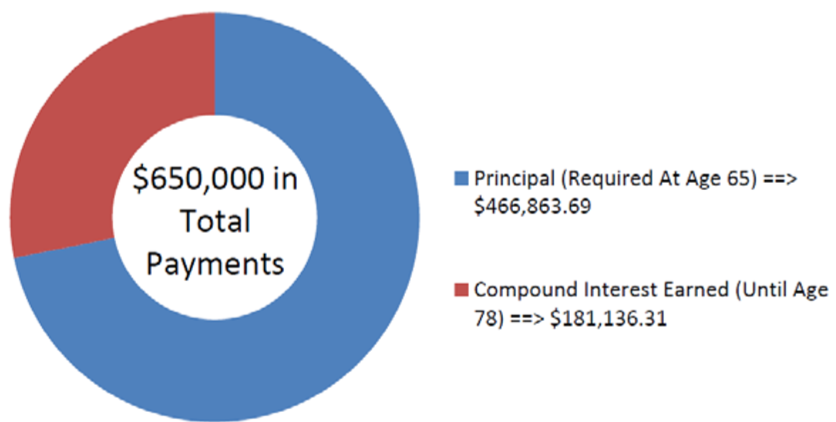
\[PV_{ORD}=\$ 50,000\left[\dfrac{1-\left[\frac{1}{(1+0.051)^{\frac{1}{1}}}\right]^{13}}{(1+0.051)^{\frac{1}{1}}-1}\right]=\$ 466,863.69 \nonumber \]
Інструкції з калькулятора
| П | В/У | ПВ | PMT | ФВ | П/У | С/У |
|---|---|---|---|---|---|---|
| 13 | 5.1 | Відповідь: -466,863.694 | 50000 | 0 | 1 | 1 |
На малюнку видно, скільки основного боргу і відсотків складають виплати. Родрігесу потрібно буде мати $466,863,69 на своєму рахунку, коли йому виповниться 65 років, якщо він хоче отримати 13 років платежів у розмірі 50 000 доларів.
Перерахуйте приклад\(\PageIndex{1}\) застосування трьох змін:
- Родрігес хоче залишити спадщину в розмірі 100 000 доларів для своїх дітей (якщо припустити, що він помирає у віці 78 років).
- Виплати проводяться на початку року.
- Його процентна ставка становить 5,1%, що ускладнюється півроку.
Розрахуйте теперішню вартість і суму відсотків.
Рішення
Крок 1:
Виплати здійснюються на початку інтервалів платежів, а період складання (піврічні) і інтервали виплат (щорічно) різні. Це тепер загальна ануїтет за рахунок. Обчисліть його значення на початку, яке є його теперішньою вартістю, або\(PV_{DUE}\).
Що ви вже знаєте
Крок 1 (продовження):
Нижче відображається шкала часу для облікового запису клієнта.

Крок 2:
\(FV\)= 100 000 доларів,\(IY\) = 5,1%,\(CY\) = 2,\(PMT\) = 50 000 доларів,\(PY\) = 1, років = 13
Як ви туди потрапите
Крок 3:
Застосувати формулу 9.1.
Крок 4:
Оскільки є майбутнє значення, застосовуйте Формулу 9.2 і Формулу 9.3.
Крок 5:
Застосовуємо Формулу 11.4 і Формулу 11.5.
Крок 6:
Для розрахунку відсотків застосовуємо і адаптуємо Формулу 8.3, де\(FV = N × PMT + FV\) і\(I = FV − PV\)
Виконувати
Крок 3:
\(i=5.1 \% \div 2=2.55 \%\)
Крок 4:
\(N=2 \times 13=26\)сполуки
\[\begin{aligned}\$ 100,000&=PV(1+0.0255)^{26} \\ PV&=\$ 100,000 \div 1.0255^{26}\\ &=\$ 51,960.42776\end{aligned} \nonumber \]
Крок 5:
\(N=1 \times 13=13\)платежі
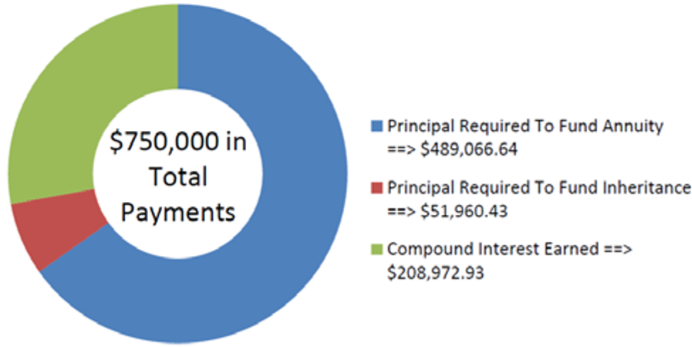
\[\begin{aligned}PV_{DUE}&=\$ 50,000\left[\dfrac{1-\left[\frac{1}{(1+0.0255)^{\frac{2}{1}}}\right]^{13}}{(1+0.0255)^{\frac{2}{1}}-1}\right] \times(1+0.0255)^{\frac{2}{1}}\\ &=\$ 489,066.6372 \end{aligned} \nonumber \]
\[PV=\$ 51,960.42776+\$ 489,066.6372=\$ 541,027.07 \nonumber \]
Крок 6:
\[\begin{aligned}I&=(13 \times \$ 50,000+\$ 100,000)-\$ 541,027.07 \\ I&=\$ 750,000-\$ 541,027.07\\ &=\$ 208,972.93 \end{aligned} \nonumber \]
Інструкції з калькулятора
| Режим | П | В/У | ПВ | PMT | ФВ | П/У | С/У |
|---|---|---|---|---|---|---|---|
| ЛВ | 13 | 5.1 | Відповідь: -541 027.065 | 50000 | 100000 | 1 | 2 |
Цифра показує, скільки основної суми та відсотків складають платежі. Родрігес вимагатиме більше грошей, потребуючи мати $541 027.07 на своєму рахунку, коли йому виповниться 65 років, якщо він хоче отримати 13 років $50,000 виплат, залишаючи спадщину $100,000 для своїх дітей. Його рахунок буде заробляти $208 972.93 протягом цього часу.
Важливі примітки
Якщо будь-яка зі змінних, включаючи, або\(IY, CY, PMT\)\(PY\), змінюється між початковою та кінцевою точкою ануїтету, або якщо буде зроблений додатковий депозит або зняття одноразового платежу, це створює новий часовий сегмент, який ви повинні розглядати окремо. Потім буде кілька часових відрізків, які вимагають від вас працювати справа наліво, повторюючи кроки з 3 по 5 в процедурі. Пам'ятайте, що теперішнє значення на початку одного часового відрізка стає майбутнім значенням в кінці наступного часового відрізка. Приклад\(\PageIndex{3}\) ілюструє це поняття.
Продовжуючи попередні два приклади, Родрігес розуміє, що під час виходу на пенсію йому потрібно зробити певний тип коригування свого річного валового доходу, щоб врахувати зростання вартості життя. Отже, він буде брати $50 000 на початку кожного року протягом шести років, потім збільшить його до $60 000 на залишок. Припустимо, його процентна ставка все ще становить 5,1% піврічних і що він все ще хоче залишити спадщину в розмірі 100 000 доларів для своїх дітей. Скільки грошей має бути в його пенсійному фонді в 65 років?
Рішення
Крок 1:
Відбувається зміна змінних через шість років. В результаті вам знадобляться два часових відрізка. В обох сегментах платежі здійснюються на початку періоду, а періоди складання і інтервали виплат різні. Це два послідовних загальних ануїтетів. Потрібно обчислити отриману теперішню величину, або\(PV_{DUE}\).
Що ви вже знаєте
Крок 1 (продовження):
Нижче відображається шкала часу для облікового запису клієнта.
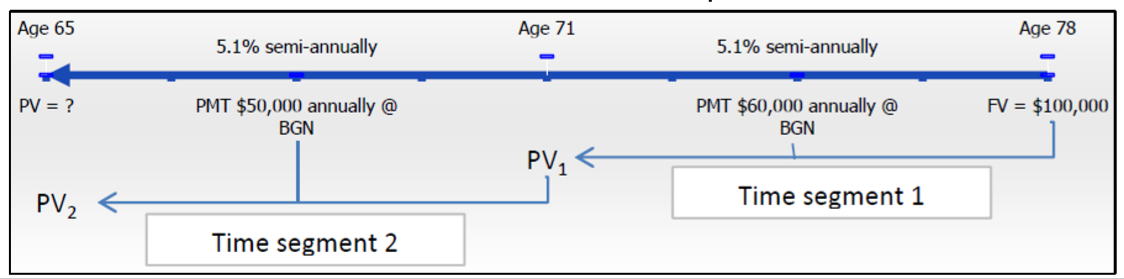
Крок 2:
Часовий відрізок 1 (починаючи з правого боку):\(FV\) = $100,000,\(IY\) = 5,1%,\(CY\)\(PMT\) = 2, = $60 000,\(PY\) = 1, років = 7
Часовий відрізок 2:\(FV = PV_1\) часового відрізка 1,\(IY\) = 5,1%,\(CY\) = 2,\(PMT\) = $50 000,\(PY\) = 1, років = 6
Як ви отримаєте
Там Для кожного часового відрізка повторіть наступні дії:
Крок 3:
Застосувати формулу 9.1.
Крок 4:
Застосовуйте формулу 9.2 та формулу 9.3.
Крок 5:
Застосовуємо Формулу 11.1 і Формулу 11.5.
Виконувати
Вперше відрізок (починаючи з правого боку):
Крок 3:
\(i=5.1 \% \div 2=2.55 \%\)
Крок 4:
\(N=2 \times 7=14\)сполуки
\[\$ 100,000=PV(1+0.0255)^{14} \nonumber \]
\[PV_1=5100,000 \div 1.0255^{14}=\$ 70,291.15736 \nonumber \]
Крок 5:
\(N=1 \times 7=7\)платежі
\[PV_{DUE 1}=\$ 60,000\left[\dfrac{1-\left[\frac{1}{(1+0.0255)^{\frac{2}{1}}}\right]^{7}}{(1+0.0255)^{\frac{2}{1}}-1}\right] \times(1+0.0255)^{\frac{2}{1}}=\$ 362,940.8778 \nonumber \]
\[\text { Total } PV_1=\$ 70,291.15736+\$ 362,940.8778=\$ 433,232.0352 \nonumber \]
Для другого сегмента часу:
Крок 3:
\(i\)залишається незмінним = 2,55%
Крок 4:
\(N=2 \times 6=12\)сполуки
\[\$ 433,232.0352=PV(1+0.0255)^{12}\nonumber \]
\[PV_{2}=\$433,232.0352 \div 1.0255^{12}=\$ 320,252.5426 \nonumber \]
Крок 5:
\(N=1 \times 6=6 \)платежі
\[PV_{DUE 2}=\$ 50,000\left[\dfrac{1-\left[\frac{1}{(1+0.0255)^{\frac{2}{1}}}\right]^{6}}{(1+0.0255)^{\frac{2}{1}}-1}\right] \times(1+0.0255)^{\frac{2}{1}}=\$ 265,489.8749 \nonumber \]
\[\text { Total } PV_{2}=\$ 320,252.5426+\$ 265,489.8749=\$ 585,742.42 \nonumber \]
Інструкції з калькулятора
| Часовий відрізок | Режим | П | В/У | ПВ | PMT | ФВ | П/У | С/У |
|---|---|---|---|---|---|---|---|---|
| 1 | ЛВ | 7 | 5.1 | Відповідь: -433 232.0352 | 60000 | 100000 | 1 | 2 |
| 2 | \(\surd\) | 6 | \(\surd\) | Відповідь: -585 742.4175 | 50000 | 433 232.0352 | \(\surd\) | \(\surd\) |
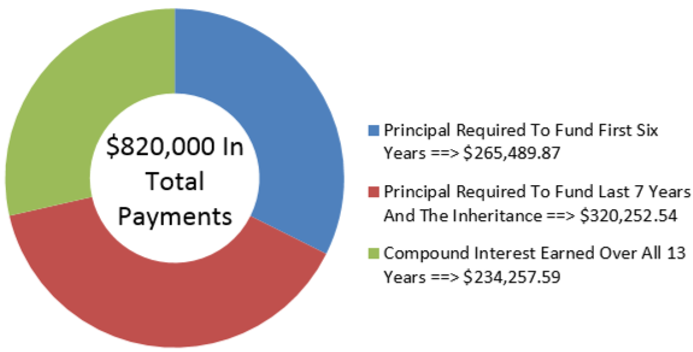
На малюнку видно, скільки основного боргу і відсотків складають виплати. Щоб його пенсійний дохід збільшився на 10 000 доларів після шести років, Родрігес повинен мати 585 742,42 доларів, інвестованих у свій пенсійний фонд у віці 65 років.
Робота з кредитами
На початку цієї глави ви придбали свій перший будинок і розпочали свій іпотечний кредит у розмірі 150 000 доларів на 5%, що складається півроку. Припустимо, ваша іпотека має п'ятирічний термін. До того, як цей термін закінчується, ви повинні почати покупки навколо в різних фінансових установах, щоб знайти найкращу ставку для вашого наступного іпотечного терміну. У цих інших фінансових установ виникне одне гостре питання: скільки ви ще заборгуєте по іпотеці і, таким чином, скільки вам потрібно позичити у них?
До цього моменту в цій главі розглядалося лише поняття інвестиційних ануїтетів. Але як щодо боргів? Всі ануїтетні поняття також відносяться до запозичення грошей. При роботі з кредитами можуть знадобитися розрахунки як майбутньої вартості, так і поточної вартості, саме тому ця тема була відкладена до цього моменту.
Як споживач, ви, ймовірно, найбільш зацікавлені в балансі, належному на будь-який з ваших боргів в будь-який момент. Сьогоднішня технологія дозволила легко дізнатися свій поточний баланс, відвідавши свій онлайн-банківський рахунок; однак банківський рахунок не допомагає вам визначити ваш майбутній баланс у певний момент часу. Щоб розібратися в цьому, потрібні ануїтетні розрахунки.
Аналогічно, підприємства весь час застосовують ануїтетні розрахунки. Постійна фінансова звітність повинна бути точною. Щоб дати уявлення про справжнє фінансове здоров'я компанії, баланси повинні відображати не тільки грошові кошти, що підлягають сплаті або дебіторській заборгованості сьогодні, але і всі майбутні грошові потоки, такі як ті, що виникають з ануїтетів. Купівля-продаж ділових договорів, таких як продаж плану споживчих платежів фінансовій установі, вимагає роботи з майбутніми платежами та дисконтування цих платежів до дати продажу договору.
У цьому розділі ви розрахуєте залишки кредиту в будь-який момент часу протягом усього терміну кредиту. Крім того, ви вивчите, як купувати та продавати кредитні договори.
Залишок за будь-яким кредитним договором
Щоб точно визначити залишок за будь-яким кредитом в будь-який момент часу, завжди починайте з початкової основної суми кредиту, а потім відніміть зроблені платежі. Це означає розрахунок майбутньої вартості з використанням процентної ставки кредиту.
Деякі можуть запитати, чому вони не можуть з'ясувати залишок кредиту, починаючи з кінця кредиту (де майбутня вартість дорівнює нулю, оскільки залишок не залишається) та обчислюючи поточну вартість непогашених платежів? Відповідь полягає в тому, що ануїтетний платіж майже завжди\(PMT\) є округленим числом (ця характеристика більш глибоко вивчена в розділі 11.4, коли ви дізнаєтеся, як розрахувати ануїтетний платіж). Тому кожен платіж має незначну невідповідність його справжньої вартості, яка накопичується з кожним наступним платежем. Наприклад, припустімо, що ви математично обчислюєте свій платіж як $500.0045. Оскільки ви не можете заплатити більше двох десяткових знаків, ваші фактичні платежі становлять $500,00. 0.0045 доларів скидається, що означає, що кожен платіж, який ви робите, становить 0,0045 доларів, що не відповідає математично необхідному. Якщо ви зробите 100 таких платежів, помилка в $0.0045 накопичується до $0.45 плюс відсотки. Це означає, що ваш останній платіж повинен бути збільшений на $0.45 або більше, щоб погасити ваш кредит. Таким чином, останній платіж - це інша сума, ніж кожен інший платіж.
Щоб ще більше ускладнити ситуацію, сума останнього платежу може бути невідомою та незліченною, особливо якщо процентні ставки змінні. Ви не можете обчислити поточну вартість з невідомого числа, а також не можете використовувати формулу ануїтету, де платіж знаходиться в іншій сумі. У главі 13 наведено набагато більш докладно про ці поняття платежів за кредитами, залишки по кредиту та різниці остаточних платежів. На даний момент можна зробити висновок, що точний розрахунок залишку кредиту досягається за допомогою формули ануїтету майбутнього значення.
Формула
Кредити - це найчастіше звичайні ануїтети, що вимагають застосування Формули 11.2 (звичайна ануїтетна майбутня вартість) для розрахунку майбутнього балансу,\(FV_{ORD}\). Це основне припущення при виконанні розрахунків по кредиту, якщо не вказано інше. У рідкісному випадку кредиту, структурованого як аннуїтет, ви застосовуєте Формулу 11.3 (ануїтет до майбутньої вартості) для обчислення майбутньої вартості\(FV_{DUE)\).
Розрахунок загальної суми сплачених відсотків за кредитом (в цілому або на будь-який часовий відрізок) ще раз вимагає адаптації Формули 8.3 (\(I = S – P = FV − PV\)), де:
- Майбутнє значення (\(FV\)) термін у формулі представляє сукупний основний капітал та відсотки разом. У кредитних ануїтетах ануїтетний платіж включає обидва ці елементи. Крім того, будь-який майбутній основний капітал, що залишився в кінці кредиту, або майбутній непогашений залишок також повинен бути врахований при розрахунку. Отже,\(FV\) на будь-якому часовому проміжку в формулі розширюється, включивши обидва ці елементи і замінюється на\(N × PMT + FV\).
- Теперішнє значення (\(PV\)) у формулі - це те, з чого ви почали. Це сума відкриття кредиту. Тому адаптація Формули 8.3 залишається такою ж, як раніше обговорювалося, і пишеться як:\[I = (N × PMT + FV) − PV \nonumber \].
Як це працює
Рішення для майбутнього залишку кредиту - це розрахунок майбутньої вартості ануїтету. Таким чином, ви використовуєте ті самі кроки, що й описано в розділі 11.2. Однак вам потрібно змінити тлумачення цих кроків для залишків кредиту. Малюнок нижче допоможе вам зрозуміти ці відмінності.

- Принципал кредиту формує поточну вартість, або\(PV\). На кроці 4, коли ви переміщуєте поточну вартість у майбутнє, ваша відповідь (\(FV\)) являє собою загальну суму, заборговану по кредиту з відсотками, ніби платежі не були здійснені.
- На кроці 5 майбутня вартість ануїтету (\(FV_{ORD}\)) являє собою загальну суму, сплачену за кредитом з відсотками. З обох\(FV\) і\(FV_{ORD}\) на тій же фокусній даті, фундаментальна концепція часу вартість грошей дозволяє потім взяти\(FV\) і відняти\(FV_{ORD}\) виробляти залишок за кредитом.
Давайте підрахуємо, що ви все ще заборгували на своєму новому будинку 150 000 доларів після п'яти років внесення щомісячних платежів у розмірі $872.41 на 5%, що складаються півроку:
Крок 1: Структура вашої іпотеки зображена на малюнку вище. Оскільки платежі йдуть в кінці періоду, а інтервал виплат і частота складання різні, у вас звичайний загальний ануїтет.
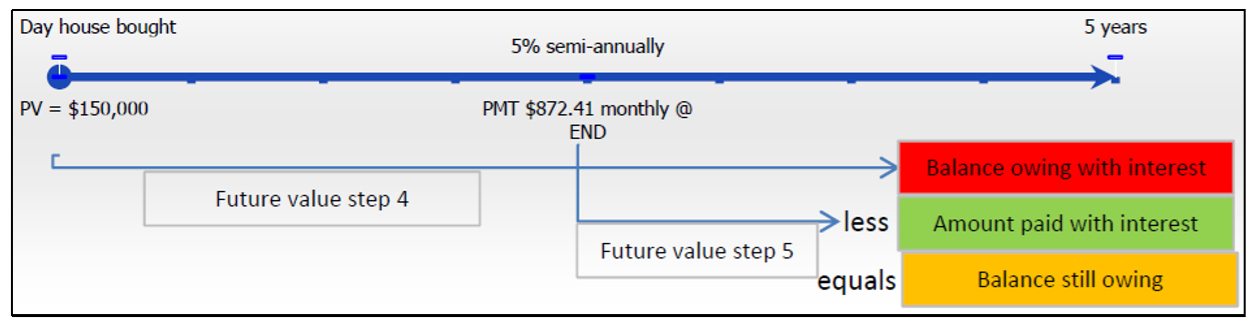
Крок 2: Відомі змінні\(PV\) = 150 000 доларів,\(IY\) = 5%,\(CY\) = 2,\(PMT\) = 872,41$,\(PY\) = 12, а роки = 5.
Крок 3: Періодична процентна ставка\(i\) = 5% ÷ 2 = 2,5%.
Крок 4:\(N\) = 2 × 5 = 10 з'єднань,\(FV\) = 150 000 доларів (1 + 0,025) 10 = 192 012,6816 доларів
Крок 5:\(N\) = 12 × 5 = 60 платежів
\[FV_{ORD}=\$ 872.41\left[\dfrac{\left[(1+0.025)^{\frac{2}{12}}\right]^{60}-1}{(1+0.025)^{\frac{2}{12}}-1}\right]=\$ 59,251.59215 \nonumber \]
Отже, якщо неоплачений кредит коштує 192 012,6816 доларів США, а ваші платежі коштують 59 251,59215 доларів, то ваш баланс все ще має $192 012,6816 − $59 251,59215 = $132 761,09. Сума сплачених відсотків становить I = (60 × $872,41 + $132,761,09) − $150 000,00 = $35,105,69. З виплатами на загальну суму $872.41 × 60 = $52,344.60, це означає, що тільки $17,238.91 фактично пішли до принципала!
Важливі примітки
Метод поточної вартості надходження до балансу. У рідкісних обставин, коли остаточний платіж точно дорівнює всім іншим ануїтетним платежам, ви можете прийти до балансу за рахунок розрахунків ануїтету поточної вартості. Однак це сувора умова повинна бути дотримано. У цьому випадку, оскільки ви починаєте в кінці позики, майбутня вартість завжди дорівнює нулю, тому, щоб повернути всі платежі до координаційної дати, вам потрібна лише формула 11.4.
Ваш калькулятор BAII+. Належне застосування конвенції про знак грошових потоків для поточної вартості та ануїтетного платежу автоматично призведе до майбутньої вартості, яка виключає основну суму кредиту та платежі. Припускаючи, що ви є позичальником, ви вводите поточну вартість (\(PV\)) як позитивне число, оскільки ви отримуєте гроші. Ви вводите ануїтетний платіж (\(PMT\)) як негативне число, оскільки ви платите гроші. Коли ви обчислюєте майбутнє значення (\(FV\)), він відображає від'ємне число, що вказує на те, що це залишок.
За будь-яким відсотковим кредитом у будь-який момент часу основна сума буде зменшена на суму, рівну здійсненим платежам, більше, ніж здійснені платежі, або менше, ніж здійснені платежі?
- Відповідь
-
Основна сума буде зменшена на суму менше, ніж платежі. Частина платежів завжди йде на відсотки, які нараховуються за кредитом.
Два роки тому Джилліан придбала новий Ford F-250 за $71,482.08 з початковим внеском у розмірі 5000 доларів, а решта фінансується через її дилерський центр Ford на 5.9% щомісяця. Вона здійснює щомісячні платежі в розмірі $1,282,20. Яким є її баланс сьогодні? Скільки відсотків вона заплатила на сьогоднішній день?
Рішення
Крок 1:
Виплати здійснюються в кінці інтервалів платежів, а період складання та інтервали виплат однакові. Тому це проста звичайна ануїтет. Обчисліть його значення через два роки після його початку, яка є його майбутньою вартістю, або\(FV_{ORD}\). Як тільки ви дізнаєтеся\(FV_{ORD}\), ви можете визначити суму відсотків, або\(I\).
Що ви вже знаєте
Крок 1 (продовження):
Графік ощадної ануїтету відображається нижче.

Крок 2:
\(PV\)= $71,482.08 − $5,000 = $66,482.08,\(IY\) = 5.9%,\(CY\) = 12,\(PMT\) = $1,282.20,\(PY\) = 12, років = 2
Як ви туди потрапите
Крок 3:
Застосувати формулу 9.1.
Крок 4:
Застосовуйте формулу 9.2 та формулу 9.3.
Крок 5:
Застосовуємо Формулу 11.1 і Формулу 11.2. Остаточне майбутнє значення - це різниця між відповідями на крок 4 і 5.
Крок 6:
Для розрахунку відсотків застосовують адаптовану Формулу 8.3, де\(I = (N × PMT + FV) − PV\).
Крок 3:
\[i=5.9 \% \div 12=0.491\overline{6} \% \nonumber \]
Крок 4:
\(N=12 \times 2=24\)сполуки
\[FV=\$ 66,482.08(1+0.00491\overline{6})^{24}=\$ 74,786.94231 \nonumber \]
Крок 5:
\(N=12 \times 2=24\)платежі
\[FV_{ORD}=\$ 1,282.20\left[\dfrac{\left.(1+0.00491 \overline{6})^{\frac{12}{12}}\right]^{24}-1}{(1+0.00491 \overline{6})^{\frac{12}{12}}-1}\right]=\$ 32,577.13179 \nonumber \]
\[FV=\$ 74,786.94231-\$ 32,577.13179=\$ 42,209.81 \nonumber \]
Крок 6:
\[\begin{aligned} I &=(24 \times \$ 1,282.20+\$ 42,209.81)-\$ 66,482.08 \\ &=\$ 72,982.61-\$ 66,482.08\\ &=\$ 6,500.53 \end{aligned} \nonumber \]
Інструкції з калькулятора
| П | В/У | ПВ | PMT | ФВ | П/У | С/У |
|---|---|---|---|---|---|---|
| 24 | 5.9 | 66482.08 | -1282.2 | Відповідь: -42 209.81052 | 12 | 12 |
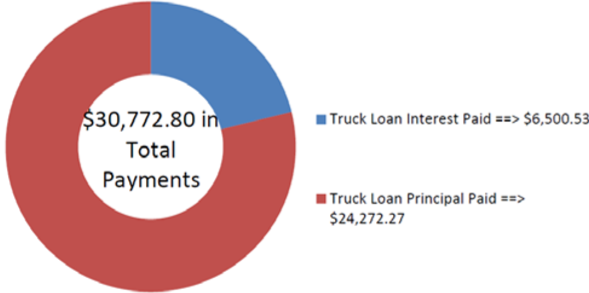
На малюнку видно, скільки основного боргу і відсотків складають виплати. Після двох років щомісячних платежів, Джилліан має баланс на Ford F-250 $42,209.81. Загалом, вона зробила $30,772.80 у вигляді платежів, з яких $6500.53 пішли на відсотки за її позикою.
Продаж кредитного договору
Зазвичай кредитні контракти продаються від роздрібних продавців до фінансових установ. Наприклад, коли споживач здійснює покупку у Sleep Country Canada за своїм планом платежів, фінансування фактично здійснюється через його партнера Citi Financial. У більшості роздрібних ситуацій це означало б, що Sleep Country Canada отримує гроші відразу, продаючи контракт Citi Financial, тоді як Citi Financial бере на себе фінансову відповідальність за збір платежів.
Коли фінансова компанія купує кредитний договір у іншої організації, вона по суті інвестує в майбутні платежі кредитного договору. Дві компанії зазвичай погоджуються на вигідну процентну ставку для фінансової компанії і використовують її для визначення суми, відомої як ціна продажу, сплачена фінансовою компанією іншій організації для придбання контракту. Цей підручник охоплює лише розрахунки фіксованої процентної ставки з відомими кінцевими сумами платежу.
Раніше обговорювалося, чим останній платіж в кредиті практично завжди відрізняється від кожного іншого платежу в ануїтетному через округлення невідповідності в сумі ануїтетного платежу. Таким чином, при продажу кредитного договору необхідно розрахувати поточну вартість всіх залишилися ануїтетних платежів (крім останнього) плюс поточну вартість скоригованого єдиного остаточного платежу, як показано на цьому малюнку.

Формула
Як видно з малюнка, потрібно два обчислення. Перший передбачає розрахунки ануїтету поточної вартості за формулою 11.4. Зверніть увагу, що ануїтет припиняє один платіж, не дотягуючи до кінця кредитного договору, тому вам потрібно використовувати,\(N − 1\) а не\(N\). Другий розрахунок передбачає розрахунок єдиного платежу за поточною вартістю за фіксованою ставкою за допомогою формули 9.3, переставленої для\(PV\). Таким чином, для завершення цього розрахунку не потрібно ніяких нових формул.
Як це працює
Кроки, що беруть участь у продажу будь-якого кредитного договору, майже ідентичні будь-якому розрахунку ренуїтету поточної вартості з лише незначними відмінностями, як зазначено нижче.
Крок 1: Без змін.
Крок 2: Визначте відомі змінні, включаючи\(PMT, PY\), і роки, разом з нещодавно узгодженими\(IY\) і\(CY\). Також визначте суму останнього платежу, яка є\(FV\).
Крок 3: Використовуйте формулу 9.1 для розрахунку\(i\).
Крок 4: Останній платіж - це той\(FV\), який ви ставитеся як до одного платежу. Застосовуйте формулу 9.2, щоб визначити,\(N\) оскільки цей крок не є розрахунком ануїтету. Перемістіть майбутнє значення на початок часового відрізка за допомогою Формули 9.3, переставляючи для\(PV\).
Крок 5: Використовуйте формулу 11.1 для обчислення\(N\) та віднімання 1, щоб зняти остаточний платіж (оскільки він враховується на кроці 4). Застосуйте Формулу 11.4 (або Формулу 11.5, якщо це ануїтет), щоб розрахувати поточну вартість. Додайте обидві поточні значення з кроків 4 та 5 разом, щоб досягти загальної поточної вартості, яка відома як загальна виручка від продажу.
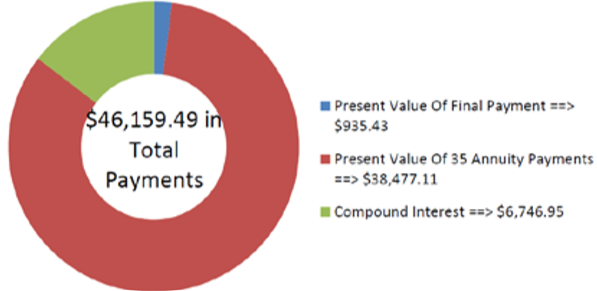
Продовжуючи покупку Jillian Ford F-250, нагадаємо, що щомісячні платежі Джилліан фіксовані на рівні $1282,20 протягом п'яти років. Припустимо, що через два роки Ford хоче продати контракт іншій фінансовій компанії, яка погоджується на облікову ставку 10,8%, що ускладнюється півріччя. Остаточний платіж Джилліан відомий на рівні $1,282,49. Які виручка від продажу?
Рішення
Крок 1:
Виплати здійснюються в кінці інтервалів платежів, а період складання (піврічні) і інтервали виплат (щомісяця) різні. Тому це звичайна загальна ануїтет. Обчисліть його вартість на дату продажу, яка є його теперішньою вартістю\(PV_{DUE}\), або, плюс поточна вартість остаточного платежу, або\(PV\).
Що ви вже знаєте
Крок 1 (продовження):
Терміни купівлі-продажу кредитного договору відображаються нижче.
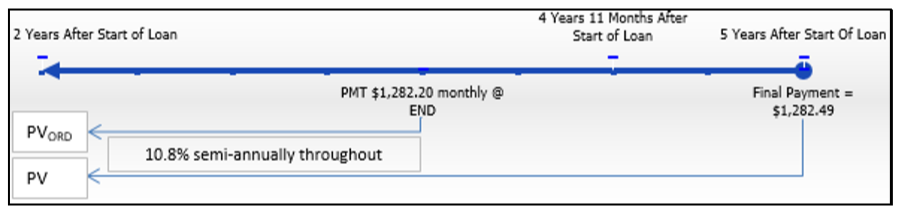
Крок 2:\(FV\) = $1,282,49,\(IY\) = 10,8%,\(CY\) = 2,\(PMT\) = $1,282,20,\(PY\) = 12, років = 3
Як ви туди потрапите
Крок 3:
Застосувати формулу 9.1.
Крок 4:
Для остаточної суми платежу застосуйте Формулу 9.2 та Формулу 9.3, переставляючи для\(PV\).
Крок 5:
Для ануїтету застосовуйте Формулу 11.1 (забираючи останній платіж) і Формулу 11.4.
Виконувати
Крок 3:
\[i=10.8 \% \div 2=5.4 \% \nonumber \]
Крок 4:
\(N=2 \times 3=6\)сполуки
\[\$ 1,282.49=PV(1+0.054)^{6} \nonumber \]
\[PV=\$ 1,282.49 \div 1.054^{6}=\$ 935.427906 \nonumber \]
Крок 5:
\(N=12 \times 3-1=35 \)платежі
\[PV_{ORD}=\$ 1,282.20\left[\dfrac{1-\left[\frac{1}{(1+0.054)^{\frac{2}{12}}}\right]^{35}}{(1+0.054)^{\frac{2}{12}}-1}\right]=\$ 38,477.10711 \nonumber \]
\[PV=\$ 935.427906+\$ 38,477.10711=\$ 39,412.54 \nonumber \]
Інструкції з калькулятора
| Елемент | П | В/У | ПВ | PMT | ФВ | П/У | С/У |
|---|---|---|---|---|---|---|---|
| Остаточний платіж | 6 | 10.8 | Відповідь: -935.427906 | 0 | 1282.49 | 2 | 2 |
| Ануїтет | 35 | \(\surd\) | Відповідь: -38 477.10711 | 1282.2 | 0 | 12 | 2 |
На малюнку показана поточна вартість і суми відсотків по угоді. Фінансова компанія заплатить $39 412,54 за контракт. Натомість він отримує 35 платежів у розмірі 1 282,20 доларів США та один платіж у розмірі 1282,49 доларів США на номінальну суму 46 159.49 доларів США.