6.6: Функції, що діють на множини

Last updated
Save as PDF

Page ID: 65549

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Попередній перегляд Діяльність 1 (Функції та набори)
Нехай$S = \{a, b, c, d\}$ і$T = \{s, t, u\}$. Визначте$f: S \to T$ по

$f(a) = s$$f(b) = t$$f(c) = t$$f(d) = s$

Нехай$A = \{a, c\}$ і$B = \{a, d\}$. Зверніть увагу, що$A$ і$B$ є підмножинами$S$. Використовуйте метод реєстру, щоб вказати елементи наступних двох підмножин$T$:

(a)$\{f(x)\ |\ x \in A\}$
(b)$\{f(x)\ |\ x \in B\}$
Нехай$C = \{s, t\}$ і$D = \{s, u\}$. Зверніть увагу, що$C$ і$D$ є підмножинами$T$. Використовуйте метод реєстру, щоб вказати елементи наступних двох підмножин$S$:

(a)$\{x \in S\ |\ f(x) \in C\}$
(b)$\{x \in S\ |\ f(x) \in D\}$

Тепер нехай$g: \mathbb{R} \to \mathbb{R}$ буде визначено$g(x) = x^2$, для кожного$x \in \mathbb{R}$.
Нехай$A = \{1, 2, 3, -1\}$. Скористайтеся методом ростера, щоб вказати елементи множини$\{g(x)\ |\ x \in A\}$.
Використовуйте метод реєстру, щоб вказати елементи кожного з наступних наборів:

(a)$\{x \in \mathbb{R}\ |\ g(x) = 1\}$
(b)$\{x \in \mathbb{R}\ |\ g(x) = 9\}$
(c)$\{x \in \mathbb{R}\ |\ g(x) = 15\}$
(d)$\{x \in \mathbb{R}\ |\ g(x) = -1\}$
Нехай$B = \{1, 9, 15, -1\}$. Скористайтеся методом ростера, щоб вказати елементи множини
\ {\ x\ in\ mathbb {R}\ |\ g (x)\ in B\}\).

Попередній перегляд діяльності 2 (Функції та інтервали)
$g: \mathbb{R} \to \mathbb{R}$ Дозволяти визначатися$g(x) = x^2$, для кожного$x \in \mathbb{R}$.

Спочатку визначимо, де g відображає замкнутий інтервал [1, 2]. (Нагадаємо, що$[1, 2] = \{x \in R\ |\ 1 \le x \le 2\}$.) Тобто опишемо, простіше кажучи, набір$\{g(x)\ |\ x \in [1, 2]\}$. Це множина всіх зображень дійсних чисел в замкнутому інтервалі [1, 2].

(a) Намалюйте графік функції за$g$ допомогою$-3 \le x \le 3$.
(б) На графіку намалюйте вертикальні лінії$x = 1$ і$x = 2$ від осі х до графіка. Позначте точки$P(1, f(1))$ і$Q(2, f (2))$ на графіку.
(c) Тепер намалюйте горизонтальні лінії від точок$P$ і$Q$ до осі y. Використовуйте цю інформацію з графіка для$\{g(x)\ |\ x \in [1, 2]\}$ опису множини простіше. Використовуйте інтервальне позначення або встановити позначення будівельника.
Тепер ми визначимо всі дійсні числа, які g відображає в замкнутому інтервалі [1, 4]. Тобто ми опишемо набір більш$\{x \in \mathbb{R}\ |\ g(x) \in [1, 4]\}$ простою мовою. Це множина всіх преобразів дійсних чисел в замкнутому інтервалі [1, 4].
(a) Намалюйте графік функції за$g$ допомогою$-3 \le x \le 3$.
(б) На графіку намалюйте горизонтальні лінії$y = 1$ і$y = 4$ від їхньої осі до графіка. Позначте всі точки, де ці дві лінії перетинають графік.
(c) Тепер намалюйте вертикальні лінії від точок у частині (2) до осі x, а потім використовуйте отриману інформацію для$\{x \in \mathbb{R}\ |\ g(x) \in [1, 4]\}$ опису множини простішими термінами. (Вам потрібно буде описати цей набір як об'єднання двох інтервалів. Використовувати інтервальне позначення або встановити позначення будівельника.)

Функції, що діють на множини

У нашому дослідженні функцій ми зосередилися на тому, як функція «відображає» окремі елементи своєї області в кодомен. Також вивчено преімідж окремого елемента в його кодомені. Наприклад, якщо$f: \mathbb{R} \to \mathbb{R}$ визначається$f(x) = x^2$, для кожного$x \in \mathbb{R}$, то

$f(2) = 4$. Ми говоримо, що$f$ карти від 2 до 4 або що 4 - це зображення 2 під функцією$f$.
Оскільки$f(2) = 4$ має на увазі$x = -2$, що$x = 2$ або, ми говоримо, що попередні зображення 4 є 2 і -2 або що набір попередніх зображень 4 є {-2, 2}.

Для функції наступним$f: S \to T$ кроком є розгляд підмножин$S$ або$T$ і те, що їм відповідає в іншому наборі. Ми зробили це в попередньому перегляді діяльності. Ми дамо деякі визначення, а потім переглянемо приклади в попередньому перегляді діяльності у світлі цих визначень. Ми спочатку розглянемо ситуацію, коли$A$ йде підмножина$S$ і розглянемо сукупність виходів, чиї входи від$A$. Це буде підмножина$T$.

Визначення

Нехай$f: S \to T$. Якщо$A \subseteq S$, то зображення$A$ під$f$ - це безліч$f(A)$, де

$f(A) = \{f(x)\ |\ x \in A\}$.

Якщо немає плутанини щодо того, яка функція використовується, ми$f(A)$ викликаємо образ$A$.

Розглянемо тепер ситуацію, в якій$C$ знаходиться підмножина$T$ і розглянемо підмножину,$A$ що складається з усіх елементів, виходи$T$ яких знаходяться в$C$.

Визначення

Нехай$f: S \to T$. Якщо$C \subseteq T$, то попереднім зображенням$C$$f$ under є набір$f^{-1}(C)$, де

$f^{-1}(C) = \{x \in S\ |\ f(x) \in C\}$.

Якщо немає плутанини щодо того, яка функція використовується, ми$f^{-1}(C)$ викликаємо preimage of$C$. Передзображення безлічі$C$ під$f$ називають також зворотним зображенням$C$ під$f$.

Зверніть увагу, що набір$f^{-1}(C)$ визначається, чи$f^{-1}$ є функція чи ні.

Перевірка прогресу 6.30 (Попередній перегляд активності$\PageIndex{1}$ Revisited)

Нехай$S = \{a, b, c, d\}$ і$T = \{s, t, u\}$. Визначте$f: S \to T$ по

$f(a) = s$$f(b) = t$$f(c) = t$$f(d) = s$.

Нехай$A = \{a, c\}$,$B = \{a, d\}$,$C = \{s, t\}$, і$D=\{s, u\}$.

Використовуйте свою роботу в режимі попереднього перегляду,$\PageIndex{1}$ щоб визначити кожен із наведених нижче наборів:

$f(A)$
$f(B)$
$f^{-1}(C)$
$f^{-1}(D)$

Відповідь: Додайте сюди тексти. Не видаляйте цей текст спочатку.

Приклад 6.31 (Зображення та зображення наборів)

$g: \mathbb{R} \to \mathbb{R}$Дозволяти визначатися$g(x) = x^2$, для кожного$x \in \mathbb{R}$. Наведені нижче результати базуються на прикладах у розділі «Активність попереднього перегляду»$\PageIndex{1}$ та «Попередній перегляд»$\PageIndex{2}$.

Нехай$A = \{1, 2, 3, -1\}$. Потім$f(A) = \{1, 4, 9\}$.
Нехай$B = \{1, 9 ,15, -1\}$. Потім$f^{-1}(B) = \{-\sqrt{15}, -3, -1, 1, 3, \sqrt{15}\}$.

Графіки з Preview Activity$\PageIndex{2}$ ілюструють наступні результати:

Якщо$T$ замкнутий інтервал [1, 2], то зображення множини$T$ дорівнює
\[\begin{array} {rcl} {f(T)} &= & {\{f(x)\ |\ x \in [1, 2]\}} \\ {} &= & {[1, 4].} \end{array}\]
Якщо$C$ замкнутий інтервал [1, 4], то попередній образ множини$C$ дорівнює
\[f^{-1}(C) = \{x \in \mathbb{R}\ |\ f(x) \in [1, 4]\} = [-2, -1] \cup [1, 2].\]

Набір операцій і функцій, що діють на множини

Зараз ми розглянемо наступну ситуацію: Дозволяти$S$ і$T$ бути множинами і нехай f буде функцією від$S$ до$T$. Крім того, нехай$A$ і$B$ бути підмножини$S$ і нехай$C$ і$D$ бути підмножинами$T$. В решті цього розділу ми розглянемо наступні ситуації і відповімо на поставлені питання в кожному конкретному випадку.

Множина$A \cap B$ є підмножиною$S$ і так$f(A \cap B$ є підмножиною$T$. Крім того,$f(A)$ і$f(B)$ є підмножинами$T$. Отже,$f(A) \cap f(B)$ є підмножиною$T$.

Чи є якісь стосунки між$f(A \cap B$ і$f(A) \cap f(B)$?
Множина$A \cup B$ є підмножиною$S$ і так$f(A \cup B$ є підмножиною$T$. Крім того,$f(A)$ і$f(B)$ є підмножинами$T$. Отже,$f(A) \cup f(B)$ є підмножиною$T$.

Чи є якісь стосунки між$f(A \cup B$ і$f(A) \cup f(B)$?
Множина$C \cap D$ є підмножиною$T$ і так$f^{-1}(C \cap D)$ є підмножиною$S$. Крім того,$f^{-1}(C)$ і$f^{-1}(D)$ є підмножинами$S$. Отже,$f^{-1}(C) \cap f^{-1}(D)$ є підмножиною$S$.

Чи існує зв'язок між множинами$f^{-1}(C \cap D)$ і$f^{-1}(C) \cap f^{-1}(D)$?
Множина$C \cup D$ є підмножиною$T$ і так$f^{-1}(C \cup D)$ є підмножиною$S$. Крім того,$f^{-1}(C)$ і$f^{-1}(D)$ є підмножинами$S$. Отже,$f^{-1}(C) \cup f^{-1}(D)$ є підмножиною$S$.

Чи існує зв'язок між множинами$f^{-1}(C \cup D)$ і$f^{-1}(C) \cup f^{-1}(D)$?

Ці та інші питання будуть розглянуті в наступній перевірці прогресу.

Перевірка прогресу 6.32 (набір операцій і функцій, що діють на множини)

У розділі 6.2 ми ввели функції, що включають конгруенції. Наприклад, якщо ми дозволимо

$\mathbb{Z}_8 = \{0, 1, 2, 3, 4, 5, 6, 7\}.$

то ми можемо визначити$f: \mathbb{Z}_8 \to \mathbb{Z}_8$ по$f(x) = r$, де$(x^2 + 2) \equiv r$ (мод 8) і$r \in \mathbb{Z}_8$. Більш того, ми скоротили це позначення до

$f(x) = (x^2 + 2)$(мод 8)

Ми будемо використовувати наступні підмножини$\mathbb{Z}_8$:

$A = \{1, 2, 4\}$$B = \{3, 4, 6\}$$C = \{1, 2, 3\}$$D = \{3, 4, 5\}$

Переконайтеся$f(0) = 2$, що$f(1) = 3$$f(2) = 6$,, і$f(3) = 3$. Потім визначають$f(4)$,$f(5)$,$f(6)$ і$f(7)$.
Визначити$f(A)$,$F=f(A=B)$,$f^{-1}(C)$, і$f^{-1}(D)$.
Для кожного з наступного визначте дві підмножини,$\mathbb{Z}_8$ а потім визначте, чи існує зв'язок між двома множинами. Наприклад,$A \cap B = \{4\}$ і з тих пір$f(4) = 2$, ми це бачимо$f(A \cap B) = \{2\}$.

(a)$f(A \cap B)$ і$f(A) \cap f(B)$
(b)$f(A \cup B)$ і$f(A) \cup f(B)$
(c)$f^{-1}(C \cap D)$ і$f^{-1}(C) \cap f^{-1}(D)$
(d)$f^{-1}(C \cup D)$ і$f^{-1}(C) \cup f^{-1}(D)$
Зверніть увагу, що$f(A)$ є підмножиною кодомену,$\mathbb{Z}_8$. Отже,$f^{-1}(f(A))$ є підмножиною домену,$\mathbb{Z}_8$. Чи існує якесь відношення між$A$ і$f^{-1}f(A))$ в цьому випадку?
Зверніть увагу, що$f^{-1}(C)$ є підмножиною кодомену,$\mathbb{Z}_8$. Отже,$f(f^{-1}(f(C))$ є підмножиною домену,$\mathbb{Z}_8$. Чи існує якесь відношення між$C$ і$f(f^{-1}f(C))$ в цьому випадку?

Відповідь: Додайте сюди тексти. Не видаляйте цей текст спочатку.

Приклад 6.33 (Множинні операції та функції, що діють на множини)

$f: \mathbb{R} \to \mathbb{R}$Визначте$f(x) = x^2 + 2$ для всіх$x \in \mathbb{R}$. Корисно буде скористатися графіком, показаним на малюнку 6.11.

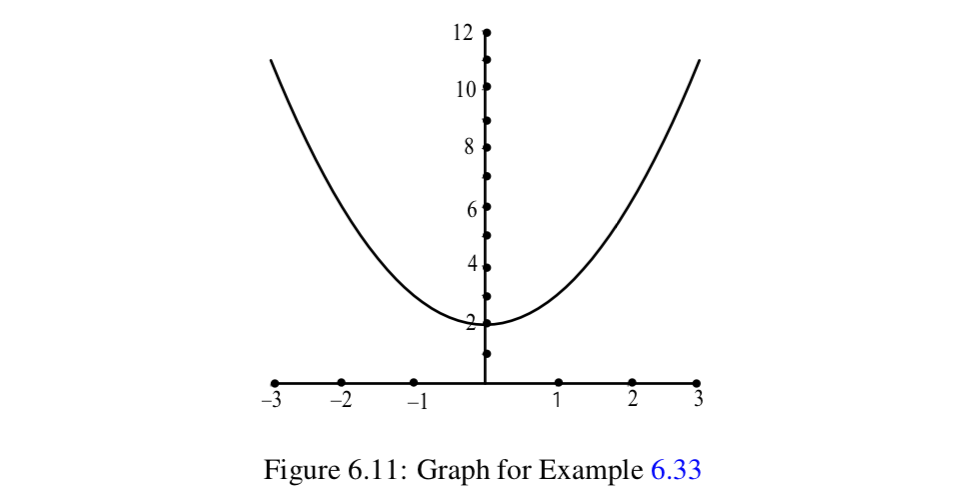
$2019-04-03 3.56.58.png$

Ми будемо використовувати такі замкнуті інтервали:

$A = [0, 3]$$B = [-2, 1]$$C = [2, 6]$$D = [0, 3]$.

Переконайтеся$f(A) = [2, 11]$$f(B) = [2, 6]$, що$f^{-1}(C) = [-2, 2]$,, і що$f^{-1}(D) = [-1, 1]$.
(а) Поясніть, чому$f(A \cap B) = [2, 3]$ і$f(A) \cap f(B) = [2, 6]$. Так що в даному випадку,$f(A \cap B) \subseteq f(A) \cap f(B)$.
(б) Поясніть, чому$f(A \cup B) = [2, 11]$ і$f(A) \cup f(B) = [2, 11]$. Так що в даному випадку,$f(A \cup B) \subseteq f(A) \cup f(B)$.
(c) Пояснити, чому$f^{-1}(C \cap D) = [-1, 1]$ і$f^{-1}(C) \cap f^{-1}(D) = [-1, 1]$. Так що в даному випадку,$f^{-1}(C \cap D) \subseteq f^{-1}(C) \cap f^{-1}(D)$.
(d) Поясніть, чому$f^{-1}(C \cup D) = [-2, 2]$ і$f^{-1}(C) \cap f^{-1}(D) = [-2, 2]$. Так що в даному випадку,$f^{-1}(C \cup D) \subseteq f^{-1}(C) \cup f^{-1}(D)$.
Згадайте, що$A = [0, 3]$. $f(A) = [2, 11]$Примітка є підмножиною кодомену,$\mathbb{R}$. Поясніть чому$f^{-1}(f(A)) = [-3, 3]$. Оскільки$f^{-1}f(A))$ це підмножина домену$\mathbb{R}$, ми бачимо, що в даному випадку,$A \subseteq f^{-1}(f(A))$.
Згадайте, що$C = [2, 6]$. $f^{-1}(C) = [-2, 2]$Примітка є підмножиною кодомену,$\mathbb{R}$. Поясніть чому$f(f^{-1}f(C)) = [2, 6]$. Оскільки$f^{-1}f(C))$ це підмножина домену$\mathbb{R}$, ми бачимо, що в даному випадку,$f(f^{-1}(C)) = C$.

Приклади в Progress Check 6.32 та Example 6.33 були призначені для ілюстрації загальних результатів про те, як функції діють на множини. Зокрема, досліджено, як дія функції на множини взаємодіє з множинами операцій перетину та об'єднання. Зараз ми викладемо теореми, які ці приклади мали на меті проілюструвати. Деякі докази залишаться в якості вправ.

Теорема 6.34.

$f: S \to T$Дозволяти бути функція і нехай$A$ і$B$ бути підмножинами$S$. Тоді

$f(A \cap B$\ підмножина f (A)\ cap f (B)\)
$f(A \cup B$= f (А)\ чашка f (B)\)

Доказ

Доведемо Частина (1). Доказом частини (2) є Вправа (5).

Припустимо, що$f: S \to T$ це функція і нехай$A$ і$B$ бути підмножинами$S$. Доведемо, що$f(A \cap B$\ subseteq f (A)\ cap f (B)\) доводячи, що для всіх$y \in T$, якщо$y \in f(A \cap B)$, то$y \in f(A) \cap f(B)$.

Ми припускаємо, що$y \in f(A \cap B)$. Це означає, що існує$x \in A \cap B$ таке, що$f(x) = y$. Оскільки$x \in A \cap B$, робимо висновок, що$x \in A$ і$x \in B$.

Оскільки$x \in A$ і$f(x) = y$, робимо висновок, що$y \in f(A)$.
Оскільки$x \in B$ і$f(x) = y$, робимо висновок, що$y \in f(B)$.

Так як$x \in f(A)$ і$y \in f(B)$,$y \in f(A) \cap f(B)$. Це доводить, що якщо$y \in f(A \cap B)$, то$y \in f(A) \cap f(B)$. Звідси$f(A \cap B$\ підмножина f (A)\ cap f (B)\).

Теорема 6.35

$f: S \to T$Дозволяти бути функція і нехай$C$ і$D$ бути підмножинами$T$. Тоді

$f^{-1}(C \cap D) = f^{-1}(C) \cap f^{-1}(D)$
$f^{-1}(C \cup D) = f^{-1}(C) \cup f^{-1}(D)$

Доказ

Доведемо Частина (2). Доказом частини (1) є Вправа (6).

Припустімо, що$f: S \to T$ є функцією і що$C$ і$D$ є підмножинами$T$. Доведемо це$f^{-1}(C \cup D) = f^{-1}(C) \cup f^{-1}(D)$ шляхом доведення того, що кожна множина є підмножиною іншого.

Ми починаємо з дозволяючи$x$ бути елементом$f^{-1}(C \cup D)$. Це означає, що$f(x)$ є елементом$C \cup D$. Отже,

$f(x) \in C$або$f(x) \in D$

У тому випадку$f(x) \in C$, коли, ми робимо висновок$x \in f^{-1}(C)$, що, а значить, що$x \in f^{-1}(C) \cup f^{-1}(D)$. У тому випадку$f(x) \in D$, коли, ми бачимо$x \in f^{-1}(D)$, що, а значить, що$x \in f^{-1}(C) \cup f^{-1}(D)$. Так в обох випадках$x \in f^{-1}(C) \cup f^{-1}(D)$, і ми довели, що$f^{-1}(C \cup D) \subseteq f^{-1}(C) \cup f^{-1}(D)$

Ми тепер пустимо$t \in f^{-1}(C) \cup f^{-1}(D)$. Це означає, що

$t \in f^{-1}(C)$або$t \in f^{-1}(D)$

У тому випадку$t \in f^{-1}(C)$, коли, ми робимо висновок, що$f(t) \in C$ і, отже, що$f(t) \in C \cup D$. Це означає, що$t \in f^{-1}(C \cup D)$.
Аналогічно, коли$t \in f^{-1}(D)$, випливає, що$f(t) \in D$ і значить, що$f(t) \in C \cup D$. Це означає, що$t \in f^{-1}(C \cup D)$.

Ці два випадки доводять, що якщо$t \in f^{-1}(C) \cup f^{-1}(D)$, то$t \in f^{-1}(C \cup D)$. Тому,$f^{-1}(C) \cup f^{-1}(D) \subseteq f^{-1}(C \cup D)$.

Оскільки ми зараз довели, що кожен з двох множин є підмножиною іншого множини, можна зробити висновок, що$f^{-1}(C \cup D) = f^{-1}(C) \cup f^{-1}(D)$.

Теорема 6.36.

$f: S \to T$Дозволяти бути функція і нехай$A$ бути підмножиною$S$ і нехай$C$ бути підмножиною$T$. Тоді

$A \subseteq f^{-1}(f(A))$
$f(f^{-1}(C)) \subseteq C$

Доказ

Доведемо Частина (1). Доказом частини (2) є Вправа (7).

Щоб довести Частина (1), доведемо, що для всіх$a \in S$, якщо$a \in A$, то$a \in f^{-1}(f(A))$. Так давайте$a \in A$. Потім, за визначенням,$f(a) \in f(A)$. Ми це знаємо$f(A) \subseteq T$, і так$f^{-1}(f(A)) \subseteq S$. Зауважте, що

$f^{-1}(f(A)) = \{x \in S\ |\ f(x) \in f(A)\}.$

Оскільки$f(a) \in f(A)$, ми використовуємо це, щоб зробити висновок$a \in f^{-1}(f(A)). This proves that if \(a \in A$, що, потім$a \in f^{-1}(f(A))$, а значить, що$A \in f^{-1}(f(A))$

Вправа 6.6

Дозволяти$f: S \to T$. нехай$A$ і$B$ бути$S$ підмножинами, і нехай$C$ і$D$ бути підмножинами$T$. Для$x \in S$ і$y \in T$, уважно поясніть, що означає сказати, що

(а)$y \in f(A \cap B)$
(b)$y \in f(A \cup B)$
(c)$y \in f(A )\cap f(B)$
(d)$y \in f(A )\cup f(B)$
(e)$x \in f^{-1}(C \cap D)$
(f) $x \in f^{-1}(C \cup D)$
(г)$x \in f^{-1}(C) \cap f^{-1}(D)$
(ч)$x \in f^{-1}(C) \cup f^{-1}(D)$
Нехай$f: \mathbb{R} \to \mathbb{R}$ мимо$f(x) = -2x + 1$. Нехай

$A = [2, 5]$$B = [-1, 3]$$C = [-2, 3]$$D = [1, 4]$.

Знайти кожне з наступного:

(a)$f(A)$
(b)$f^{-1}(f(A))$
(c)$f^{-1}(C)$
(d)$f(f^{-1}(C))$
(e)$f(A \cap B)$
(f)$f(A )\cap f(B)$
(г)$f^{-1}(C \cap D)$
(ч)$f^{-1}(C) \cap f^{-1}(D)$
Нехай$g: \mathbb{N} \times \mathbb{N} \to \mathbb{N}$ мимо$g(m, n) = 2^m 3^n$, нехай$A = \{1, 2, 3\}$, і нехай$C = \{1, 4, 6, 9, 12, 16, 18\}$. Знайти

(а)$g(A \times A)$
(б)$g^{-1}(C)$
(с)$g^{-1}(g(A \times A))$
(г)$g(g^{-1}(C))$
(а) Нехай$S = \{1, 2, 3, 4\}$. Визначте$F: S \to \mathbb{N}$ по$F(x) = x^2$ для кожного$x \in s$. Що таке діапазон функції$F$ і що таке$F(S)$? Як порівнюються ці два набори?

Тепер нехай$A$ і$B$ бути встановлює і нехай$f: A \to B$ буде довільна функція від$A$ до$B$.

(б) Поясніть, чому$f(A) = \text{range}(f)$.
(c) Визначте функцію$g: A \to f(A)$$g(x) = f(x)$ для всіх$x$ в$A$. Доведіть, що функція$g$ є surjection.
Доведіть частину (2) теореми 6.34.
$f: S \to T$Дозволяти бути функція і нехай$A$ і$B$ бути підмножинами$S$. Потім$f(A \cup B) = f(A) \cup f(B)$.
Доведіть частину (1) теореми 6.35.
$f: S \to T$Дозволяти бути функція і нехай$C$ і$D$ бути підмножинами$T$. Потім$f^{-1}(C \cup D) = f^{-1}(C) \cup f^{-1}(D)$.
Доведіть частину (2) теореми 6.36.
$f: S \to T$Дозволяти бути функція і нехай$C \subseteq T$. Потім$f(f^{-1}(C)) \subseteq C$.
Дозволяти$f: S \to T$ і нехай$A$ і$B$ бути підмножинами$S$. Довести або спростувати кожне з наступного:

(а) Якщо$A \subseteq B$, то$f(A) \subseteq f(B)$.
(б) Якщо$f(A) \subseteq f(B)$, то$A \subseteq B$.
Дозволяти$f: S \to T$ і нехай$C$ і$D$ бути підмножинами$T$. Довести або спростувати кожне з наступного:

(а) Якщо$C \subseteq D$, то$f^{-1}(C) \subseteq f^{-1}(D)$.
(б) Якщо$f^{-1}(C) \subseteq f^{-1}(D)$, то$C \subseteq D$.
Довести або спростувати:
Якщо$f: S \to T$ функція і$A$ і$B$ є підмножинами$S$, то
$f(A) \cap f(B) \subseteq f(A \cap B)$.
Примітка: Частина (1) теореми 6.34 стверджує, що$f(A \cap B) \subseteq f(A) \cap f(B)$.
Якщо$f: S \to T$ функція, нехай$A \subseteq S$, і нехай$C \subseteq T$.
(а) Частина (1) теореми 6.36 стверджує, що$A \subseteq f^{-1}(f(A))$. Наведемо приклад де$f^{-1}(f(A)) \notsubseteq A$.
(b) Частина (2) теореми 6.36 стверджує, що$f(f^{-1}(C)) \subseteq C$. Наведемо приклад де$C \notsubseteq f(f^{-1}(C))$.
Чи є таке твердження істинним чи хибним? Обгрунтуйте свій висновок доказом або контрприкладом.
Якщо$f: S \to T$ ін'єкція і$A \subseteq S$, то$f^{-1}(f(A)) = A$.
Чи є таке твердження істинним чи хибним? Обгрунтуйте свій висновок доказом або контрприкладом.
Якщо$f: S \to T$ ін'єкція і$C \subseteq T$, то$f^{-1}(f(C)) = C$.
Нехай (f: S\ to T\). Доведіть, що$f(A \cap B) = f(A) \cap f(B)$ для всіх підмножин$A$ і$B$$S$ якщо і тільки якщо$f$ ін'єкція.

Відповідь: Додайте сюди тексти. Не видаляйте цей текст спочатку.

Визначення

Визначення

Перевірка прогресу 6.30 (Попередній перегляд активності\(\PageIndex{1}\) Revisited)

Приклад 6.31 (Зображення та зображення наборів)

Перевірка прогресу 6.32 (набір операцій і функцій, що діють на множини)

Приклад 6.33 (Множинні операції та функції, що діють на множини)

Теорема 6.34.

Теорема 6.35

Теорема 6.36.

Вправа 6.6