6.4: Склад функцій

Last updated
Save as PDF

Page ID: 65553

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

АКТИВНІСТЬ ПОПЕРЕДНЬОГО ПЕРЕГЛЯДУ$\PageIndex{1}$: Constructing a New Function

Нехай$A = \{a, b, c, d\}$,$B = \{p, q, r\}$, і$C = \{s, t, u, v\}$. Діаграма стрілок на малюнку 6.6 показує дві функції:$f: A \to B$ і$g: B \to C$. Зверніть увагу, що якщо$x \in A$, то$f(x) \in B$. Так як$f(x) \in B$, ми можемо застосувати функцію$g$ до$f(x)$, і ми отримуємо$g(f(x))$, яка є елементом$C$.

Використовуючи цей процес, визначити$g(f(a))$,$g(f(b))$,,$g(f(c))$, і$g(f(d))$. Потім поясніть, як ми можемо використовувати цю інформацію для визначення функції від$A$ до$C$.

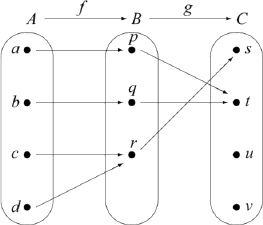
$imageedit_3_6667660914.png$

Малюнок 6.6: Діаграма стрілок, що показує дві функції

АКТИВНІСТЬ ПОПЕРЕДНЬОГО ПЕРЕГЛЯДУ$\PageIndex{1}$: Verbal Descriptions of Functions

Виходи більшості реальних функцій, які ми вивчали на попередніх курсах математики, визначалися математичними виразами. У багатьох випадках можна використовувати ці вирази, щоб дати покрокові словесні описи того, як обчислити виходи. Наприклад, якщо

$f: \mathbb{R} \to \mathbb{R}$визначається$f(x) = (3x + 2)^3$,

ми могли б описати, як обчислити виходи наступним чином:

Крок	Словесний опис	Символічний результат
1	Виберіть вхідні дані.	$x$
2	Помножте на 3.	$3x$
3	Додайте 2.	$3x + 2$
4	Куб отриманого результату.	$(3x + 3)^3$

Повні покрокові словесні описи для кожної з наступних функцій.

$f: \mathbb{R} \to \mathbb{R}$по$f(x) = \sqrt{3x^2 + 2}$, для кожного$x \in \mathbb{R}$.
$g: \mathbb{R} \to \mathbb{R}$по$g(x) = \sin(3x^2 + 2)$, для кожного$x \in \mathbb{R}$.
$h: \mathbb{R} \to \mathbb{R}$по$h(x) = e^{3x^2 + 2}$, для кожного$x \in \mathbb{R}$.
$G: \mathbb{R} \to \mathbb{R}$по$G(x) = \ln(x^4 + 3)$, для кожного$x \in \mathbb{R}$.
$k: \mathbb{R} \to \mathbb{R}$по$k(x) = \sqrt[3] {\dfrac{\sin(4x + 3)}{x^2 + 1}}$, для кожного$x \in \mathbb{R}$.

склад функцій

Існує кілька способів об'єднання двох існуючих функцій для створення нової функції. Наприклад, в численні ми навчилися формувати добуток і частку двох функцій, а потім як використовувати правило добутку для визначення похідної добутку двох функцій і часткового правила для визначення похідної частки двох функцій. Правило ланцюга в численні використовувалося для визначення похідної складу двох функцій, і в даному розділі ми зупинимося лише на складі двох функцій. Потім ми розглянемо деякі результати про складах ін'єкцій і уколів.

Основна ідея композиції функції полягає в тому, що, коли$f$ це можливо, вихід функції використовується як вхід функції$g$. Це можна назвати «$f$подальшим$g$» і називається складом$f$ і$g$. На попередніх курсах математики ми використовували цю ідею для визначення формули складу двох реальних функцій.

Наприклад, якщо

$f(x) = 3x^2 + 2$і$g(x) = sin x$

то ми можемо обчислити$g(f(x))$ наступним чином:

\[\begin{array} {rcl} {g(f(x))} &= & {g(3x^2 + 2)}\\ {} &= & {sin(3x^2 + 2).} \end{array}\]

У цьому випадку$f(x)$, вихід функції$f$, використовувався як вхід для функції$g$. Наведемо тепер формальне визначення складу двох функцій.

Визначення: композитна функція

Дозволяти$A$$B$, і$C$ бути непорожніми множинами, і нехай$f: A \to B$ і$g: B \to C$ бути функції. Склад$f$ і$g$ - це функція,$g \circ f: A \to C$ визначена

$(g \circ f)(x) = g(f(x))$

для всіх$x \in A$. Ми часто називаємо функцію$g \circ f$ складеною функцією.

Корисно думати про складену функцію$g \circ f$ як "$f$слідом$g$». Потім ми$f$ називаємо внутрішньою функцією і$g$ зовнішньою функцією.

Схеми композиції та стрілок

Поняття композиції двох функцій можна проілюструвати стрілочними діаграмами, коли область і кодомен функцій є невеликими кінцевими множинами. Хоча термін «композиція» тоді не використовувався, це було зроблено в Preview Activity$\PageIndex{1}$, і тут наведено інший приклад.

Нехай$A = \{a, b, c, d\}$,$B = \{p, q, r\}$, і$C = \{s, t, u, v\}$. Діаграма стрілок на малюнку 6.7 показує дві функції:$f: A \to B$ і$g: B \to C$.

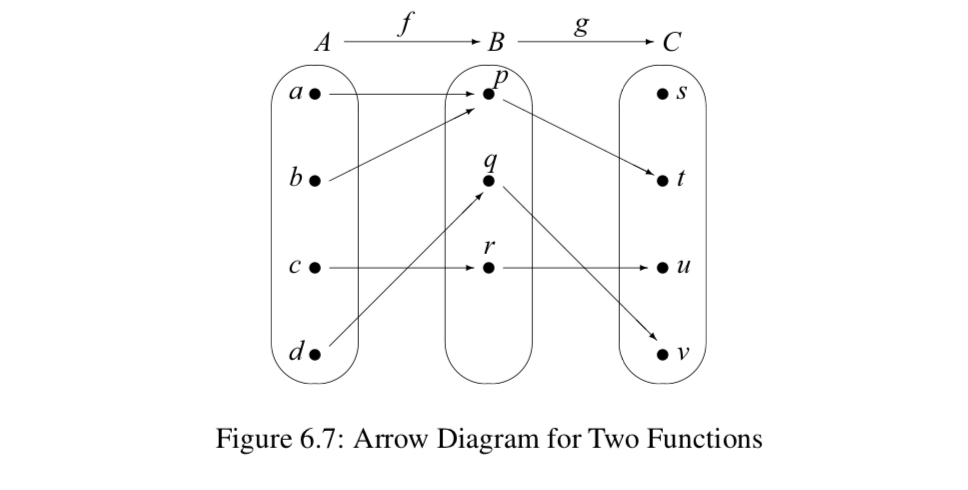
$2019-04-01 4.00.46.PNG$

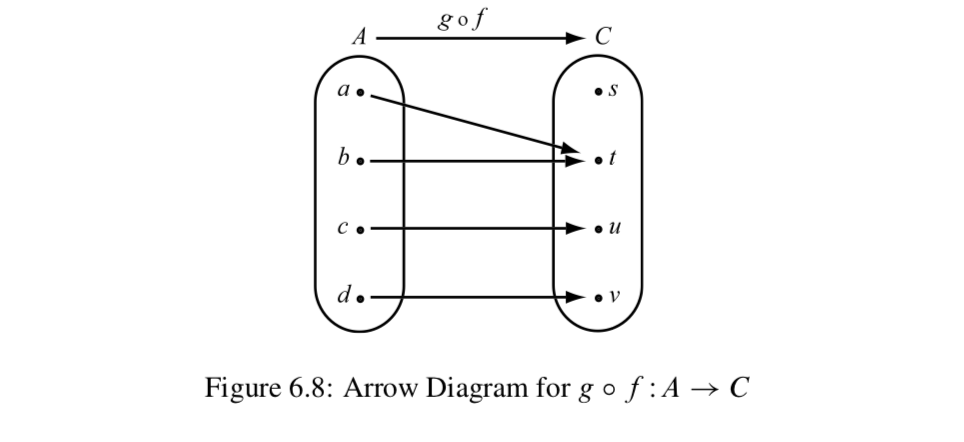
Якщо слідувати стрілкам від набору$A$ до набору$C$, ми будемо використовувати виходи$f$ як входи$g$, і отримаємо стрілку діаграми від$A$ до$C$ показаної на малюнку 6.8. Ця діаграма являє собою композицію$f$ слідом за ним$g$.

$2019-04-01 4.01.53.png$

Перевірка прогресу 6.17 (Склад двох функцій)

Нехай$A = \{a, b, c, d\}$ і$B = \{1, 2, 3\}$. Визначте функцію$f$ і$g$ наступним чином:

$f: A \to B$визначається$f(a) = 2$,$f(b) = 3$,$f(c) = 1$, і$f(d) = 2$.

$g: A \to B$визначається$g(1) = 3$. $g(2) = 1$, і$g(3) = 2$.

Створення діаграм стрілок для функції$f$,$g$,$g \circ f$, і$g \circ g$.

Відповідь: Додайте сюди тексти. Не видаляйте цей текст спочатку.

Функції розкладання

Ми використовуємо правило ланцюга в численні, щоб знайти похідну від складеної функції. Першим кроком у процесі є розпізнавання заданої функції як складеної функції. Це можна зробити різними способами, але робота в Preview Activity$\PageIndex{2}$ може бути використана для розкладання функції таким чином, що добре працює з правилом ланцюга. Використання термінів «внутрішня функція» та «зовнішня функція» також може бути корисним. Ідея полягає в тому, що ми використовуємо останній крок у процесі для представлення зовнішньої функції, а кроки до цього представляють внутрішню функцію. Отже, для функції,

$f: \mathbb{R} \to \mathbb{R}$по$f(x) = (3x + 2)^3$,

останнім кроком в таблиці словесного опису було кубик результату. Це означає, що ми будемо використовувати функцію$g$ (функцію кубінга) як зовнішню функцію і будемо використовувати попередні кроки як внутрішню функцію. Внутрішню функцію ми позначимо по$h$. Таким чином, ми$h: \mathbb{R} \to \mathbb{R}$ пропустимо$h(x) = 3x + 2$ і$g: \mathbb{R} \to \mathbb{R}$ мимо$g(x) = x^3$. Тоді

\[\begin{array} {rcl} {(g \circ h)(x)} &= & {g(h(x))} \\ {} &= & {g(3x + 2)} \\ {} &= & {(3x + 2)^3} \\ {} &= & {f(x).} \end{array}\]

Ми бачимо, що$g \circ h = f$ і, отже, ми «розклали» функцію$f$. Слід зазначити, що існують і інші способи запису функції$f$ як композиції з двох функцій, але тільки що описаний спосіб - той, який добре працює з правилом ланцюга. В цьому випадку правило ланцюга дає

\[\begin{array} {rcl} {f \prime (x)} &= & {(g \circ h)\prime (x)} \\ {} &= & {g \prime (h(x)) h \prime(x)} \\ {} &= & {3(h(x))^2 \cdot 3} \\ {} &= & {g(3x + 2)^2} \end{array}\]

Перевірка прогресу 6.18 (Розкладання функцій

Запишіть кожну з наступних функцій як склад двох функцій.

$F: \mathbb{R} \to \mathbb{R}$по$F(x) = (x^2 + 3)^3$
$G: \mathbb{R} \to \mathbb{R}$по$G(x) = In(x^2 + 3)$
$f: \mathbb{Z} \to \mathbb{Z}$по$f(x) = |x^2 - 3|$
$g: \mathbb{R} \to \mathbb{R}$по$g(x) = cos(\dfrac{2x - 3}{x^2 + 1})$

Відповідь: Додайте сюди тексти. Не видаляйте цей текст спочатку.

Теореми про складові функції

Якщо$f: A \to B$ і$g: B \to C$, то ми можемо сформувати складену функцію$g \circ f: A \to C$. У розділі 6.3 ми дізналися про ін'єкціях і відрижках. Тепер ми досліджуємо, який тип функції$g \circ f$ буде, якщо функції$f$ і$g$ є ін'єкціями (або відхиленнями).

Перевірка прогресу 6.19: Склади ін'єкцій та відмовлень

Хоча можуть бути використані інші уявлення функцій, корисно буде використовувати діаграми стрілок для представлення функцій у цій перевірці прогресу. Ми будемо використовувати наступні набори:

$A = \{a, b, c\}$,$B = \{p, q, r\}$,$C = \{u,v, w, x\}$, і$D = \{u, v\}$.

Намалюйте діаграму зі стрілками для функції$f: A \to B$, яка є ін'єкцією та діаграму зі стрілками для функції$g: B \to C$, яка є ін'єкцією. У цьому випадку композитна функція - це$g \circ f: A \to C$ ін'єкція? Поясніть.
Намалюйте діаграму зі стрілками для функції$f: A \to B$, яка є surjection, і діаграму стрілок для функції$g: B \to D$, яка є surjection. У цьому випадку композитна функція є$g \circ f: A \to D$ відсмоктуванням? Поясніть.
Намалюйте діаграму зі стрілками для функції$f: A \to B$, яка є біекцією, та діаграму стрілок для функції$g: B \to A$, яка є біекцією. У цьому випадку композитна функція$g \circ f: A \to A$ bijection? Поясніть.

Відповідь: Додайте сюди тексти. Не видаляйте цей текст спочатку.

У Progress Check 6.19 ми досліджували деякі властивості композитних функцій, пов'язаних з ін'єкціями, відбитками та біекціями. Наступна теорема містить результати, які ці дослідження мали на меті проілюструвати. Деякі докази будуть включені в вправи.

Теорема 6.20.

Дозволяти$A$$B$, і$C$ бути непорожніми множинами і припустити, що$f: A \to B$ і$g: B \to C$.

Якщо$f$ і$g$ є обидва уколу, то$(g \circ f): A \to C$ робиться ін'єкція.
Якщо$f$ і$g$ є обидва припущення, то$(g \circ f): A \to C$ це відмова.
Якщо$f$ і$g$ є обидва біекції, то$(g \circ f): A \to C$ це біекція.

Доказ

Доказом частини (1) є Вправа (6).

Частина (3) є прямим наслідком перших двох частин. Ми обговоримо процес побудови доказу частини (2). Використовуючи процес вперед-назад, ми спочатку дивимося на висновок умовного оператора в частині (2). Мета полягає в тому, щоб довести, що$g \circ f$ це відмова. Оскільки$(g \circ f): A \to C$, це еквівалентно доведенню того, що

Для всіх$c \in C$ існує$a \in A$ таке, що$(g \circ f)(a) = c$.

Оскільки в цьому твердженні в зворотному процесі використовується універсальний квантор, ми будемо використовувати метод choose-an-element і виберемо довільний елемент$c$ в множині$C$. Мета зараз полягає в тому, щоб знайти$a \in A$ таке, що$(g \circ f)(a) = c$.

Тепер ми можемо подивитися на гіпотези. Зокрема, ми припускаємо, що обидва$f: A \to B$ і$g: B \to C$ є відмови. Оскільки ми вибрали$c \in C$ і$g: B \to C$ є відривом, ми знаємо, що

існує$b \in B$ таке, що$g(b) = c$.

Тепер$b \in B$ і$f: A \to B$ є відривом. Звідси

існує$a \in A$ таке, що$f(a) = b$.

Якщо ми зараз обчислюємо$(g \circ f)(a)$, ми побачимо, що

$(g \circ f)(a) = g(f(a)) = g(b) = c$.

Тепер ми можемо написати доказ наступним чином:

Доказ теореми 6.20, частина (2)

Дозволяти$A$$B$, і$C$ бути непорожніми множинами і припустити, що$f: A \to B$ і$g: B \to C$ обидва припущення. Доведемо, що$g \circ f: A \to C$ це відмова.

$c$Дозволяти бути довільним елементом$C$. Доведемо, що існує$a \in A$ таке$(g \circ f)(a) = c$. Оскільки$g: B \to C$ це відмова, ми робимо висновок, що

існує$b \in B$ таке, що$g(b) = c$.

Тепер$b \in B$ і$f: A \to B$ є відривом. Звідси

існує$a \in A$ таке, що$f(a) = b$.

Тепер ми бачимо, що

\[\begin{align*} {(g \circ f)(a)} &= & {g(f(a))} \\ {} &= & {g(b)} \\ {} &= & {c.} \end{align*}\]

Зараз ми показали, що для кожного існує$a \in A$ таке$c \in C$, що$(g \circ f)(a) = c$, і це доводить, що$g \circ f$ це відмова.

Теорема 6.20 показує нам, що якщо$f$ і$g$ є обома спеціальними типами функцій, то склад,$f$ за яким слідують, також$g$ є таким типом функції. Наступне питання: «Якщо склад,$f$ за яким слідують,$g$ - це ін'єкція (або surjection), чи можемо ми зробити будь-який висновки про$f$ чи$g$?» Часткова відповідь на це питання дається в теоремі 6.21. Ця теорема буде досліджена та доведена в дослідженнях та діяльності для цього розділу. Див. Вправа (10).

Теорема 6.21