6.3: Ін'єкції, відмови та відхилення
- Page ID
- 65548
Функції часто використовуються в математиці для визначення та опису певних зв'язків між множинами та іншими математичними об'єктами. Крім того, функції можуть використовуватися для накладення певних математичних структур на множини. У цьому розділі ми вивчимо спеціальні типи функцій, які використовуються для опису цих зв'язків, які називаються ін'єкціями і відмовляннями. Перш ніж визначити ці типи функцій, ми переглянемо те, що говорить нам визначення функції, і дослідимо певні функції з кінцевими доменами.
Нехай\(A\) і\(B\) будуть набори. З огляду на функцію\(f : A \to B\), ми знаємо наступне:
- Для кожного\(x \in A\),\(f(x) \in B\). Тобто кожен елемент\(A\) є входом для функції\(f\). Це також можна констатувати наступним чином: Для кожного існує\(y \in B\) таке\(x \in A\), що\(y = f(x)\).
- Для даного\(x \in A\), існує рівно один\(y \in B\) такий, що\(y = f(x)\).
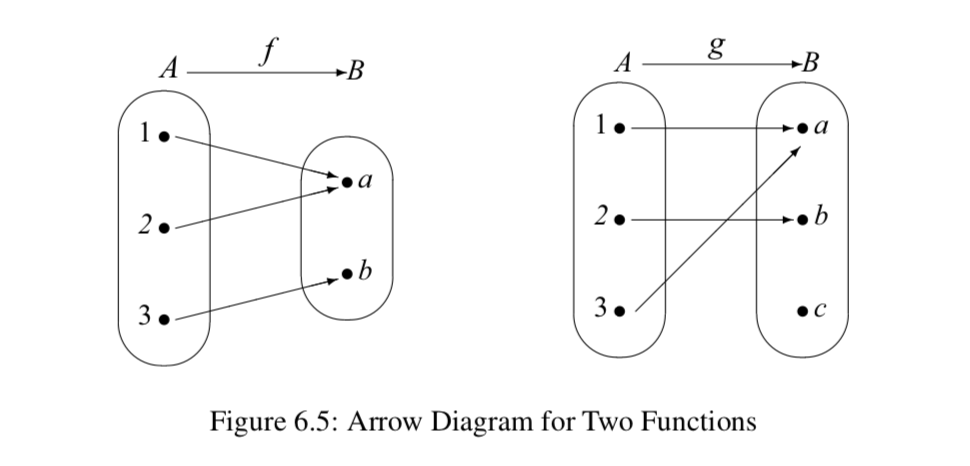
Визначення функції не вимагає, щоб різні входи видавали різні виходи. Тобто можна мати\(x_1, x_2 \in A\) з\(x1 \ne x_2\) і\(f(x_1) = f(x_2)\). Діаграма стрілок для функції на\(f\) малюнку 6.5 ілюструє таку функцію.
Також визначення функції не вимагає, щоб діапазон функції дорівнював кодомену. Діапазон завжди є підмножиною кодомену, але ці дві множини не повинні бути рівними. Тобто якщо\(g: A \to B\), то можна мати\(y \in B\) таку, що\(g(x) \ne y\) для всіх\(x \in A\). Діаграма зі стрілками для функції g на малюнку 6.5 ілюструє таку функцію.
Тепер нехай\(A = \{1, 2, 3\}\)\(B = \{a, b, c, d\}\), і\(C = \{s, t\}\). Визначте
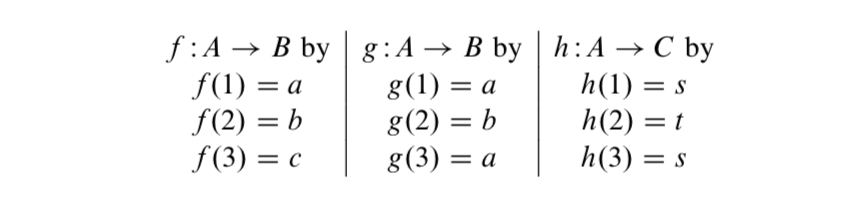
- Які з цих функцій задовольняють наступну властивість для функції\(F\)?
Для всіх\(x, y \in \text{dom}(F)\), якщо\(x \ne y\), то\(F(x) \ne F(y)\). - Які з цих функцій задовольняють наступну властивість для функції\(F\)?
Для всіх\(x, y \in \text{dom}(F)\), якщо\(F(x) = F(y)\), то\(x = y\). - Визначте діапазон виконання кожної з цих функцій.
- Які з цих функцій мають свій діапазон, рівний їхньому кодомену?
- Яка з цих функцій задовольняє наступну властивість для функції\(F\)?
Для всіх\(y\) в\(F\) кодомені існує\(x \in \text{dom}(F\)\) такий, що\(F(x) = y\).
\(B\)Дозволяти\(A\) і бути непорожніми множинами і нехай\(f: A \to B\). У попередньому перегляді активності ми визначили\(\PageIndex{1}\), чи задовольняють певні функції деяким зазначеним властивостям. Ці властивості були написані у вигляді заяв, і ми зараз розглянемо ці твердження більш детально.
- Розглянемо наступне твердження:
Для всіх\(x, y \in A\), якщо\(x \ne y\), то\(f(x) \ne f(y)\).
(а) Напишіть контрапозитив цього умовного твердження.
(б) Напишіть заперечення цього умовного твердження. - Тепер розглянемо твердження:
Для всіх існує\(x \in A\) таке\(y \in B\), що\(f(x) = y\).
Напишіть заперечення цього твердження. - Дозвольте\(g: \mathbb{R} \to \mathbb{R}\) визначитися\(g(x) = 5x + 3\), для всіх\(x \in \mathbb{R}\). Заповніть наступні докази наступних пропозицій щодо функції\(g\).
Пропозиція 1. Для всіх\(a, b \in \mathbb{R}\), якщо\(g(a) = g(b)\), то\(a = b\).
Доказ. Ми пустимо\(a, b \in \mathbb{R}\), і припускаємо, що\(g(a) = g(b)\) і доведе це\(a = b\). Так як\(g(a) = g(b)\), ми знаємо, що
\[5a + 3 = 5b + 3.\]
(Тепер доведіть, що в цій ситуації,\(a = b\).)
Пропозиція 2. Для всіх\(b \in \mathbb{R}\) існує\(a \in \mathbb{R}\) таке, що\(g(a) = b\).
Доказ. Ми пускаємо\(b \in \mathbb{R}\). Доведемо, що існує\(a \in \mathbb{R}\) таке, що\(g(a) = b\) шляхом побудови такого\(a\) в\(\mathbb{R}\). Для того, щоб це сталося, нам потрібно\(g(a) = 5a + 3 = b\).
(Тепер вирішити рівняння для\(a\) а потім показати, що для цього дійсного числа\(a\),\(g(a) = b\).)
Ін'єкції
У попередніх розділах та в Preview Activity ми бачили приклади функцій\(\PageIndex{1}\), для яких існують різні входи, які дають однаковий результат. Використовуючи більш формальні позначення, це означає, що існують функції,\(f: A \to B\) для яких існують\(x_1, x_2 \in A\) з\(x_1 \ne x_2\) і\(f(x_1) = f(x_2)\). Робота в попередньому перегляді діяльності мала на меті мотивувати наступне визначення.
\(f: A \to B\)Дозволяти бути функцією від множини\(A\) до множини\(B\). Функція\(f\) називається ін'єкцією за умови, що
для всіх\(x_1, x_2 \in A\), якщо\(x_1 \ne x_2\), то\(f(x_1) \ne f(x_2)\).
Коли\(f\) це ін'єкція, ми також говоримо, що\(f\) це функція один до одного, або\(f\) це ін'єкційна функція.
Зверніть увагу, що умова, яка вказує, що функція\(f\) є ін'єкцією, задається у вигляді умовного оператора. Як ми побачимо, в доказах зазвичай простіше використовувати контрапозитив цього умовного твердження. Хоча ми тоді не визначили термін, ми вже написали контрапозитивний для умовного твердження у визначенні ін'єкції в частині (1) попереднього перегляду активності\(\PageIndex{2}\). У цій діяльності попереднього перегляду ми також написали заперечення визначення ін'єкції. Нижче наведено резюме цієї роботи, що дає умови для\(f\) того, щоб бути ін'єкцією або не бути ін'єкцією.
Нехай\(f: A \to B\)
«\(f\)Функція - ін'єкція» означає, що
- для всіх\(x_1, x_2 \in A\), якщо\(x_1 \ne x_2\), то\(f(x_1) \ne f(x_2)\); або
- для всіх\(x_1, x_2 \in A\), якщо\(f(x_1) = f(x_2)\), то\(x_1 = x_2\).
«Функція не\(f\) є ін'єкцією» означає, що
- Існують\(x_1, x_2 \in A\) такі, що\(x_1 \ne x_2\) і\(f(x_1) = f(x_2)\).
Тепер, коли ми визначили, що це означає для функції, щоб бути ін'єкцією, ми бачимо, що в частині (3) Preview Activity\(\PageIndex{2}\), ми довели, що функція\(g: \mathbb{R} \to \mathbb{R}\) є ін'єкцією, де\(g(x/) = 5x + 3\) для всіх\(x \in \mathbb{R}\). Використовуйте визначення (або його заперечення), щоб визначити, чи є такі функції ін'єкціями.
- \(k: A \to B\), де\(A = \{a, b, c\}\)\(B = \{1, 2, 3, 4\}\), і\(k(a) = 4, k(b) = 1\), і\(k(c) = 3\).
- \(f: A \to C\), де\(A = \{a, b, c\}\)\(C = \{1, 2, 3\}\), і\(f(a) = 2, f(b) = 3\), і\(f(c) = 2\).
- \(F: \mathbb{Z} \to \mathbb{Z}\)визначено\(F(m) = 3m + 2\) для всіх\(m \in \mathbb{Z}\)
- \(h: \mathbb{R} \to \mathbb{R}\)визначено\(h(x) = x^2 - 3x\) для всіх\(x \in \mathbb{R}\)
- \(s: \mathbb{Z}_5 \to \mathbb{Z}_5\)визначено\(sx) = x^3\) для всіх\(x \in \mathbb{Z}_5\)
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Відхилення
У попередніх розділах та в Preview Activity\(\PageIndex{1}\) ми бачили, що існують функції\(f: A \to B\) для якого діапазону\((f) = B\). Це означає, що кожен елемент\(B\) є виходом функції f для деякого входу з множини\(A\). Використовуючи квантори, це означає\(y \in B\), що для кожного існує\(x \in A\) таке, що\(f(x) = y\). Однією з цілей попередньої діяльності було мотивувати наступне визначення.
\(f: A \to B\)Дозволяти бути функцією від множини\(A\) до множини\(B\). Функція\(f\) називається surjection за умови, що діапазон\(f\) дорівнює кодомену\(f\). Це означає, що
для кожного\(y \in B\) існує\(x \in A\) таке, що\(f(x) = y\).
Коли\(f\) це surjection, ми також говоримо, що\(f\) це функція ono або що\(f\) карти\(A\) на\(B\). Ми також говоримо, що\(f\) це суб'єктивна функція.
Одна з умов, яка вказує, що функція\(f\) є surjection, дається у вигляді універсально кількісного твердження, який є первинним твердженням, що використовується для доведення функції є (або не є) surjection. Хоча ми тоді не визначили термін, ми вже написали заперечення для твердження, що визначає відхилення в частині (2) попереднього перегляду активності\(\PageIndex{2}\). Тепер ми підсумовуємо умови для\(f\) того, щоб бути відстороненням чи не бути відстороненням.
Нехай\(f: A \to B\)
«Функція\(f\) - це відмова» означає, що
- діапазон (\(f\)) = codom\((f) = B\); або
- Для кожного\(y \in B\) існує\(x \in A\) таке, що\(f(x) = y\).
«Функція не\(f\) є відривом» означає, що
- rang (\(f\))\ ne codom (\(f\)); або
- Існує\(y \in B\) таке, що для всіх\(x \in A\),\(f(x) \ne y\).
Ще один важливий тип функції - це коли функція є одночасно ін'єкцією та відсмоктуванням. Цей тип функції називається біекцією.
Біекція - це функція, яка є одночасно ін'єкцією і впорскуванням. Якщо функція\(f\) є біекцією, ми також говоримо, що\(f\) один до одного і на, і\(f\) це двооб'єктивна функція.
Тепер, коли ми визначили, що це означає для функції, щоб бути surjection, ми бачимо, що в Part (3) Preview Activity\(\PageIndex{2}\), ми довели, що функція\(g: \mathbb{R} \to \mathbb{R}\) є surjection, де\(g(x) = 5x + 3\) для всіх\(x \in \mathbb{R}\). Визначте, чи є наступні функції відхиленнями.
- \(k: A \to B\), де\(A = \{a, b, c\}\)\(B = \{1, 2, 3, 4\}\), і\(k(a) = 4, k(b) = 1\), і\(k(c) = 3\).
- \(f: \mathbb{R} \to \mathbb{R}\)визначено\(f(x) = 3x + 2\) для всіх\(x \in \mathbb{R}\).
- \(F: \mathbb{Z} \to \mathbb{Z}\)визначено\(F(m) = 3m + 2\) для всіх\(m \in \mathbb{Z}\).
- \(s: \mathbb{Z}_5 \to \mathbb{Z}_5\)визначено\(s(x) = x^3\) для всіх\(x \in \mathbb{Z}_5\).
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Важливість домену та кодомену
Функції в наступних двох прикладах проілюструють, чому область і кодомен функції так само важливі, як правило, що визначає виходи функції, коли нам потрібно визначити, чи є функція surjection.
Дозвольте\(f: \mathbb{R} \to \mathbb{R}\) визначитися з\(f(x) = x^2 + 1\). Зауважте, що
\(f(2) = 5\)і\(f(-2) = 5\).
Цього достатньо, щоб довести, що функція не\(f\) є ін'єкцією, оскільки це показує, що існують два різних входи, які виробляють однаковий вихід.
З тих пір\(f(x) = x^2 + 1\), ми знаємо, що\(f(x) \ge 1\) для всіх\(x \in \mathbb{R}\). Це означає, що функція не\(f\) є відривом. Наприклад, -2 знаходиться в кодомені\(f\) і\(f(x) \ne -2\) для всіх\(x\) в домені\(f\).
Нехай\(T = \{y \in \mathbb{R}\ |\ y \ge 1\}\), і визначте\(F: \mathbb{R} \to T\) по\(F(x) = x^2 + 1\). Як і в прикладі 6.12, функція не\(F\) є ін'єкцією, оскільки\(F(2) = F(-2) = 5\).
Чи є функція\(F\) відсмоктування? Тобто, робить\(F\) карту\(\mathbb{R}\) на\(T\)? Як і в прикладі 6.12, ми знаємо, що\(F(x) \ge 1\) для всіх\(x \in \mathbb{R}\).
Щоб побачити, чи це відмова, ми повинні визначити, чи правда\(y \in T\), що для кожного існує\(x \in \mathbb{R}\) таке, що\(F(x) = y\). Тому вибираємо\(y \in T\). Мета полягає в тому, щоб визначити, чи існує\(x \in \mathbb{R}\) таке, що
\[\begin{array} {rcl} {F(x)} &= & {y, \text { or}} \\ {x^2 + 1} &= & {y.} \end{array}\]
Один із способів продовжити роботу назад і вирішити останнє рівняння (якщо можливо) для\(x\). Роблячи так, отримуємо
\(x^2 = y - 1\)
\(x = \sqrt{y - 1}\)або\(x = -\sqrt{y - 1}.\)
Тепер, з тих пір\(y \in T\), ми знаємо, що\(y \ge 1\) і, отже, що\(y - 1 \ge 0\). Це означає, що\(\sqrt{y - 1} \in \mathbb{R}\). Отже, якщо ми використовуємо\(x = \sqrt{y - 1}\), то\(x \in \mathbb{R}\), і
\[\begin{array} {rcl} {F(x)} &= & {F(\sqrt{y - 1})} \\ {} &= & {(\sqrt{y - 1})^2 + 1} \\ {} &= & {(y - 1) + 1} \\ {} &= & {y.} \end{array}\]
Це доводить, що\(F\) це відмова, оскільки ми показали\(y \in T\), що для всіх існує
\(x \in \mathbb{R}\)такий, що\(F(x) = y\). Зауважте\(y \in T\), що для кожного це було конструктивним доказом існування\(x \in \mathbb{R}\) такого, що\(F(x) = y\).
У прикладах 6.12 і 6.13 для визначення виходів функцій використовувалася та ж математична формула. Однак одна функція не була surjection, а інша - surjection. Це ілюструє важливий факт того, що чи є функція суб'єктивною, залежить не тільки від формули, яка визначає вихід функції, а й від області та кодомену функції.
Наступний приклад покаже, що чи є функція ін'єкцією, також залежить від області функції.
Нехай\(\mathbb{Z}^{\ast} = \{x \in \mathbb{Z}\ |\ x \ge 0\} = \mathbb{N} \cup \{0\}\). Визначте\(g: \mathbb{Z}^{\ast} \to \mathbb{N}\) по\(g(x) = x^2 + 1\). (Зверніть увагу, що це та сама формула, яка використовується в прикладах 6.12 та 6.13.) Нижче наведено таблицю значень для деяких входів для функції\(g\).
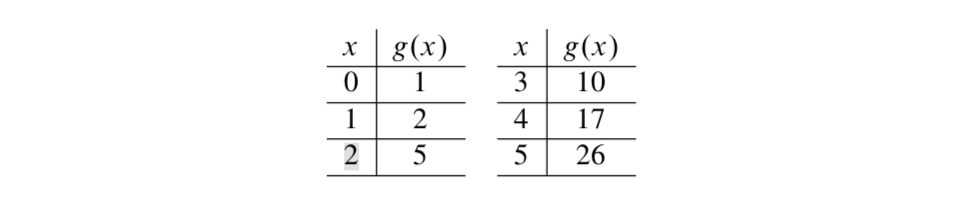
Зверніть увагу, що кодомен є\(\mathbb{N}\), і таблиця значень говорить про те, що деякі натуральні числа не є виходами цієї функції. Отже, виявляється, що функція не\(g\) є відривом.
Щоб довести, що g не є surjection, вибрати елемент\(\mathbb{N}\), який, здається, не знаходиться в діапазоні. Ми будемо використовувати 3, і ми будемо використовувати доказ протиріччя, щоб довести, що немає х в домені (\(\mathbb{Z}^{\ast}\)) такий, що\(g(x) = 3\). Таким чином, ми припускаємо, що існує\(x \in \mathbb{Z}^{\ast}\) з\(g(x) = 3\). Тоді
\[\begin{array} {rcl} {x^2 + 1} &= & {3} \\ {x^2} &= & {2} \\ {x} &= & {\pm \sqrt{2}.} \end{array}\]
Але це неможливо з тих пір\(\sqrt{2} \notin \mathbb{Z}^{\ast}\). Тому немає\(x \in \mathbb{Z}^{\ast}\) з\(g(x) = 3\). Це означає, що для кожного\(x \in \mathbb{Z}^{\ast}\),\(g(x) \ne 3\). Тому 3 не знаходиться в діапазоні\(g\), а значить, і не\(g\) є відривом.
Таблиця значень говорить про те, що різні входи дають різні виходи, а значить,\(g\) це ін'єкція. Щоб довести, що\(g\) це ін'єкція, припустимо, що\(s, t \in \mathbb{Z}^{\ast}\) (домен) с\(g(s) = g(t)\). Тоді
\[\begin{array} {rcl} {s^2 + 1} &= & {t^2 + 1} \\ {s^2} &= & {t^2.} \end{array}\]
Так як\(s, t \in \mathbb{Z}^{\ast}\), ми знаємо, що\(s \ge 0\) і\(t \ge 0\). Отже, попереднє рівняння означає, що\(s = t\). Значить,\(g\) відбувається ін'єкція.
Функції в трьох попередніх прикладах використовували одну і ту ж формулу для визначення виходів. Функції в іспит- ples 6.12 і 6.13 не ін'єкції, але функція в прикладі 6.14 є ін'єкцією. Це ілюструє важливий факт, що чи є функція ін'єкційною, залежить не тільки від формули, яка визначає вихід функції, але і від області функції.
Нехай\(R^{+} = \{y \in \mathbb{R}\ |\ y > 0\}\). Визначте
\ [\ почати {масив} {rcl} {f} &: & {\ mathbb {R}\ до\ mathbb {R}\ текст {по} f (x) = e^ {-x},\ текст {для кожного} х\ в\ mathbb {R},\ текст {і}}\\ {g} &: & {\ mathbb {R}\ до\ mathbb {R}\ thbb {R} ^ {+}\ текст {по} g (x) = e^ {-x},\ текст {для кожного} x\ in\ mathbb {R}.}
Визначте, чи є кожна з цих функцій ін'єкцією або відсмоктуванням. Обгрунтуйте свої висновки. Примітка: Перш ніж писати докази, може бути корисно намалювати графік\(y = e^{-x}\). Розумний графік можна отримати за допомогою\(-3 \le x \le 3\) і\(-2 \le y \le 10\). Будь ласка, майте на увазі, що графік не підтверджує ваші висновки, але може допомогти вам прийти до правильних висновків, які все одно потребуватимуть доказів.
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
Робота з функцією двох змінних
Потрібен час і практика, щоб стати ефективними при роботі з формальними визначеннями ін'єкції та відсмоктування. Як ми бачили, важливі всі частини функції (домен, кодомен і правило визначення виходів). Особливо це стосується функцій двох змінних.
Наприклад, визначаємо\(f: \mathbb{R} \times \mathbb{R} \to \mathbb{R} \times \mathbb{R}\) по
\(f(a, b) = (2a + b, a - b)\)для всіх\((a, b) \in \mathbb{R} \times \mathbb{R}\).
Зверніть увагу, що як домен, так і кодомен цієї функції є множиною\(\mathbb{R} \times \mathbb{R}\). Таким чином, входи і виходи цієї функції є впорядкованими парами дійсних чисел. Наприклад,
\(f(1, 1) = (3, 0)\)і\(f(-1, 2) = (0, -3)\).
Щоб дослідити, чи\(f\) є ін'єкція, ми припускаємо\((a, b) \in \mathbb{R} \times \mathbb{R}\), що\((c, d) \in \mathbb{R} \times \mathbb{R}\), і\(f(a,b) = f(c,d)\). Це означає, що
\((2a + b, a - b) = (2c + d, c - d)\).
Оскільки це рівняння є рівністю впорядкованих пар, ми бачимо, що
\[\begin{array} {rcl} {2a + b} &= & {2c + d, \text{ and }} \\ {a - b} &= & {c - d.} \end{array}\]
Склавши відповідні сторони двох рівнянь в цій системі, отримаємо\(3a = 3c\) і, отже,\(a = c\). Підставляючи\(a = c\) в будь-яке рівняння в системі дають нам\(b = d\). Оскільки\(a = c\) і\(b = d\), робимо висновок, що
\((a, b) = (c, d)\).
Отже, ми показали, що якщо\(f(a, b) = f(c, d)\), то\((a, b) = (c, d)\). Тому\(f\) проводиться ін'єкція.
Тепер, щоб визначити, чи\(f\) є surjection\((r, s) \in \mathbb{R} \times \mathbb{R}\), давайте, де\((r, s)\) вважається довільним елементом співдомену функції f. Чи можемо ми знайти впорядковану пару\((a, b) \in \mathbb{R} \times \mathbb{R}\) таку, що\(f(a, b) = (r, s)\)? Працюючи назад, ми бачимо, що для того, щоб це зробити, нам потрібно
\((2a + b, a - b) = (r, s).\)
Тобто нам потрібно
\(2a + b = r\)і\(a - b = s\).
Рішення цієї системи для\(a\) і\(b\) прибутковості
\(a = \dfrac{r + s}{3}\)і\(b = \dfrac{r - 2s}{3}\).
Так як\(r, s \in \mathbb{R}\), можна зробити висновок, що\(a \in \mathbb{R}\)\(b \in \mathbb{R}\) і, отже, що\((a, b) \in \mathbb{R} \times \mathbb{R}\).
Тепер нам потрібно перевірити, що для. ці значення\(a\) і\(b\), ми отримуємо\(f(a, b) = (r, s)\). Так
\[\begin{array} {rcl} {f(a, b)} &= & {f(\dfrac{r + s}{3}, \dfrac{r - 2s}{3})} \\ {} &= & {(2(\dfrac{r + s}{3}) + \dfrac{r - 2s}{3}, \dfrac{r + s}{3} - \dfrac{r - 2s}{3})} \\ {} &= & {(\dfrac{2r + 2s + r - 2s}{3}, \dfrac{r + s - r + 2s}{3})} \\ {} &= & {(r, s).} \end{array}\]
Це доводить\((r, s) \in \mathbb{R} \times \mathbb{R}\), що для всіх існує\((a, b) \in \mathbb{R} \times \mathbb{R}\) таке\(f(a, b) = (r, s)\). Значить, функція\(f\) - це відсмоктування. Оскільки\(f\) це і ін'єкція, і ін'єкція, це біекція.
Дозвольте\(g: \mathbb{R} \times \mathbb{R} \to \mathbb{R}\) визначитися\(g(x, y) = 2x + y\), для всіх\((x, y) \in \mathbb{R} \times \mathbb{R}\).
Примітка: Будьте обережні! Однією з основних відмінностей між цією функцією та попереднім прикладом є те\(g\), що для функції codomain є\(\mathbb{R}\), not\(\mathbb{R} \times \mathbb{R}\). Непогано почати з обчислення декількох виходів для декількох входів (і пам'ятайте, що входи - це впорядковані пари).
- Зверніть увагу, що впорядкована пара\((1, 0) \in \mathbb{R} \times \mathbb{R}\). Тобто (1, 0) знаходиться в області\(g\). Також зауважте, що\(g(1, 0) = 2\). Чи можна знайти іншу впорядковану пару\((a, b) \in \mathbb{R} \times \mathbb{R}\) таку, що\(g(a, b) = 2\)?
- Нехай\(z \in \mathbb{R}\). Потім\((0, z) \in \mathbb{R} \times \mathbb{R}\) і так\((0, z) \in \text{dom}(g)\). Тепер визначте\(g(0, z)\)?
- Функція - це\(g\) ін'єкція? Чи є функція\(g\) відсмоктування? Обгрунтуйте свої висновки.
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
- (a) Намалюйте діаграму зі стрілками, яка представляє функцію, яка є ін'єкцією, але не є відривом.
(b) Намалюйте діаграму зі стрілками, яка представляє функцію, яка є ін'єкцією і є відсмоктуванням.
(c) Намалюйте діаграму зі стрілками, яка представляє функцію, яка не є ін'єкцією і не є відривом.
(d) Намалюйте діаграму зі стрілками, яка представляє функцію, яка не є ін'єкцією, а є відривом.
(e) Намалюйте діаграму зі стрілками, яка представляє функцію, яка не є біекцією. - Нехай\(\mathbb{Z}_5 = \{0, 1, 2, 3, 4\}\) і нехай\(\mathbb{Z}_6 = \{0, 1, 2, 3, 4, 5\}\). Для кожної з наступних функцій визначте, чи є функція ін'єкцією, і визначити, чи є функція surjection. Обгрунтуйте всі висновки.
(а)\(f: \mathbb{Z}_5 \to \mathbb{Z}_5\) по\(f(x) = x^2 + 4\) (мод 5), для всіх\(x \in \mathbb{Z}_5\)
(б)\(g: \mathbb{Z}_6 \to \mathbb{Z}_6\) по\(g(x) = x^2 + 4\) (мод 6), для всіх\(x \in \mathbb{Z}_6\)
(c)\(F: \mathbb{Z}_5 \to \mathbb{Z}_5\) по\(F(x) = x^3 + 4\) (мод 5), для всіх\(x \in \mathbb{Z}_5\) - Для кожної з наступних функцій визначте, чи є функція ін'єкцією, і визначити, чи є функція surjection. Обгрунтуйте всі висновки.
(а)\(f: \mathbb{Z} \to \mathbb{Z}\) визначено\(f(x) = 3x + 1\), для всіх\(x \in \mathbb{Z}\).
(б)\(F: \mathbb{Q} \to \mathbb{Q}\) визначено\(F(x) = 3x + 1\), для всіх\(x \in \mathbb{Q}\).
(c)\(g: \mathbb{R} \to \mathbb{R}\) визначено\(g(x) = x^3\), для всіх\(x \in \mathbb{R}\).
(d)\(G: \mathbb{Q} \to \mathbb{Q}\) визначено\(G(x) = x^3\), для всіх\(x \in \mathbb{Q}\).
(е)\(k: \mathbb{R} \to \mathbb{R}\) визначено\(k(x) = e^{-x^2}\), для всіх\(x \in \mathbb{R}\).
(f)\(K: \mathbb{R}^{\ast} \to \mathbb{R}\) визначено\(K(x) = e^{-x^2}\), для всіх\(x \in \mathbb{R}^{\ast}\).
Примітка:\(\mathbb{R}^{\ast} = \{x \in \mathbb{R}\ |\ x \ge 0\}.\)
(g)\(K_1: \mathbb{R}^{\ast} \to T\) визначається\(K_1(x) = e^{-x^2}\), для всіх\(x \in \mathbb{R}^{\ast}\), де\(T = \{y \in \mathbb{R}\ |\ 0 < y \le 1\}\).
(h)\(h: \mathbb{R} \to \mathbb{R}\) визначається\(h(x) = \dfrac{2x}{x^2 + 4}\), для всіх\(x \in \mathbb{R}\).
(i)\(H: \{x \in \mathbb{R}\ |\ x \ge 0\} \to \{y \in \mathbb{R}\ |\ 0 \le y \le \dfrac{1}{2}\}\) визначено\(H(x) = \dfrac{2x}{x^2 + 4}\), для всіх\(x \in \{x \in \mathbb{R}\ |\ x \ge 0\}\). - Для кожної з наступних функцій визначте, чи є функція біекцією. Обгрунтуйте всі висновки.
(а)\(F: \mathbb{R} \to \mathbb{R}\) визначено\(F(x) = 5x + 3\), для всіх\(x \in \mathbb{R}\).
(б)\(G: \mathbb{Z} \to \mathbb{Z}\) визначено\(G(x) = 5x + 3\), для всіх\(x \in \mathbb{Z}\).
(c)\(f: (\mathbb{R} - \{4\}) \to \mathbb{R}\) визначено\(f(x) = \dfrac{3x}{x - 4}\), для всіх\(x \in (\mathbb{R} - \{4\})\).
(d)\(g: (\mathbb{R} - \{4\}) \to (\mathbb{R} - \{3\})\) визначено\(g(x) = \dfrac{3x}{x - 4}\), для всіх\(x \in (\mathbb{R} - \{4\})\). - Нехай\(s: \mathbb{N} \to \mathbb{N}\), де для кожного\(n \in \mathbb{N}\),\(s(n)\) це сума різних натуральних дільників числа\(n\). Це сума функції дільників, яка була введена в попередній перегляд діяльності\(\PageIndex{2}\) з розділу 6.1. Це\(s\) ін'єкція? Це\(s\) відмова? Обгрунтуйте свої висновки.
- \(d: \mathbb{N} \to \mathbb{N}\)Дозволяти\(d(n)\), де число натуральних дільників числа\(n\). Це функція кількості дільників, введена у Вправі (6) з розділу 6.1. Функція - це\(d\) ін'єкція? Чи є функція\(d\) відсмоктування? Обгрунтуйте свої висновки.
- У попередньому перегляді активності\(\PageIndex{2}\) з розділу 6.1 ми ввели функцію дня народження. Чи є функція дня народження ін'єкцією? Це відмова? Обгрунтуйте свої висновки.
- (а)\(f: \mathbb{Z} \times \mathbb{Z} \to \mathbb{Z}\) Дозволяти визначатися\(f(m,n) = 2m + n\). Функція - це\(f\) ін'єкція? Чи є функція\(f\) відсмоктування? Обгрунтуйте свої висновки.
(b)\(g: \mathbb{Z} \times \mathbb{Z} \to \mathbb{Z}\) Дозволяти визначатися\(g(m,n) = 6m + 3n\). Функція - це\(g\) ін'єкція? Чи є функція\(g\) відсмоктування? Обгрунтуйте свої висновки. - (а)\(f: \mathbb{R} \times \mathbb{R} \to \mathbb{R} \times \mathbb{R}\) Дозволяти визначатися\(f(x,y) = (2x, x + y)\). Функція - це\(f\) ін'єкція? Чи є функція\(f\) відсмоктування? Обгрунтуйте свої висновки.
(b)\(g: \mathbb{Z} \times \mathbb{Z} \to \mathbb{Z} \times \mathbb{Z}\) Дозволяти визначатися\(g(x,y) = (2x, x + y)\). Функція - це\(g\) ін'єкція? Чи є функція\(g\) відсмоктування? Обгрунтуйте свої висновки. - \(f: \mathbb{R} \times \mathbb{R} \to \mathbb{R}\)Дозволяти бути функція\(f(x, y) = -x^2y + 3y\), визначена, для всіх\((x, y) \in \mathbb{R} \times \mathbb{R}\). Чи є функція\(f\) і ін'єкція? Чи є функція\(f\) відсмоктування? Обгрунтуйте свої висновки.
- \(g: \mathbb{R} \times \mathbb{R} \to \mathbb{R}\)Дозволяти бути функція\(g(x, y) = (x^3 + 2)sin y\), визначена, для всіх\((x, y) \in \mathbb{R} \times \mathbb{R}\). Чи є функція\(g\) і ін'єкція? Чи є функція\(g\) відсмоктування? Обгрунтуйте свої висновки.
- \(A\)Дозволяти бути непорожнім набором. Функція ідентичності на множині\(A\), позначається\(I_A\), є функцією,\(I_A: A \to A\) визначеною\(I_A (x) = x\) для кожного\(x\) in\(A\). Це\(I_A\) ін'єкція? Це\(I_A\) відмова? Обгрунтуйте свої висновки.
- \(B\)Дозволяти\(A\) і бути двома непорожніми множинами. Визначте
\[p_1: A \times B \to A \text{ by } p_1(a, b) = a\]
для кожного\((a, b) \in A \times B\). Це перша проекційна функція, введена у Вправі (5) у розділі 6.2.
(а) Чи є функція\(p_1\) відсмоктування? Обгрунтуйте свій висновок.
(b) Якщо\(B = \{b\}\), чи є функція\(p_1\) ін'єкцією? Обгрунтуйте свій висновок.
(c) За яких умов функція\(p_1\) не є ін'єкцією? Складіть здогадки і доведіть це. - Визначити\(f: \mathbb{N} \to \mathbb{Z}\) слід наступним чином: Для кожного\(n \in \mathbb{N}\),
\[f(n) = \dfrac{1 + (-1)^n (2n - 1)}{4}.\]
Чи є функція\(f\) ін'єкцією? Чи є функція\(f\) відсмоктування? Обгрунтуйте свої висновки.
Пропозиції. Почніть з обчислення декількох виходів для функції, перш ніж намагатися написати доказ. Вивчаючи, чи є функція ін'єкцією, це може бути гарною ідеєю використовувати випадки, засновані на тому, чи є входи парними чи непарними. Вивчаючи, чи є f surjection, розгляньте можливість використання випадків, заснованих на тому, чи є вихід позитивним або меншим або дорівнює нулю. - \(C\)Дозволяти множина всіх дійсних функцій, які є неперервними на замкнутому інтервалі [0, 1]. Визначте функцію\(A: C \to \mathbb{R}\) наступним чином: Для кожного\(f \in C\).
\[A(f) = \int_0^1 f(x)dx.\]
Функція - це\(A\) ін'єкція? Це відмова? Обгрунтуйте свої висновки. - Нехай\(A = \{(m, n)\ |\ m \in \mathbb{Z}, n \in \mathbb{Z}, \text{ and } n \ne 0\}\). Визначте\(f: A \to \mathbb{Q}\) наступним чином:
Для кожного\((m, n) \in A\),\(f(m, n) = \dfrac{m + n}{n}\).
(а) Чи є функція ін'єкції? Обгрунтуйте свій висновок.
(b) Чи є функція відмови? Обгрунтуйте свій висновок. - Оцінка доказів
Див. інструкцію до вправи (19) на сторінці 100 з розділу 3.1.
Пропозиція. Функція,\(f: \mathbb{R} \times \mathbb{R} \to \mathbb{R} \times \mathbb{R}\)\(f(x, y) = (2x + y, x - y)\) визначена, - це ін'єкція.
- Доказ
-
Для кожного\((a, b)\) і\((c, d)\) в\(\mathbb{R} \times \mathbb{R}\), якщо\(f(a, b) = f(c, d)\), то
\((2a + b, a - b) = (2c + d, c - d).\)
Ми будемо використовувати системи рівнянь, щоб довести, що\(a = c\) і\(b = d\).
\[\begin{array} {rcl} {2a + b} &= & {2c + d} \\ {a - b} &= & {c - d} \\ {3a} &= & {3c} \\ {a} &= & {c} \end{array}\]
З тих пір\(a = c\), ми бачимо, що
\((2c + b, c - b) = (2c + d, c - d).\)
Отже\(b = d\). Тому ми довели, що функція\(f\) - це ін'єкція.
Пропозиція. Функція,\(f: \mathbb{R} \times \mathbb{R} \to \mathbb{R} \times \mathbb{R}\)\(f(x, y) = (2x + y, x - y)\) визначена, є surjection.
- Доказ
-
Нам потрібно знайти впорядковану пару таку, що\(f(x, y) = (a, b)\) для кожного\((a, b)\) в\(\mathbb{R} \times \mathbb{R}\). Тобто нам потрібно\((2x + y, x - y) = (a, b)\), або
\(2x + y = a\)і\(x - y = b\).
Розглядаючи ці два рівняння як систему рівнянь і вирішуючи для\(x\) і\(y\), ми знаходимо, що
\(x = \dfrac{a + b}{3}\)і\(y = \dfrac{a - 2b}{3}\).
Отже,\(x\) і\(y\) є дійсними числами\((x, y) \in \mathbb{R} \times \mathbb{R}\), і
\[\begin{array} {rcl} {f(x, y)} &= & {f(\dfrac{a + b}{3}, \dfrac{a - 2b}{3})} \\ {} &= & {(2(\dfrac{a + b}{3}) + \dfrac{a - 2b}{3}, \dfrac{a + b}{3} - \dfrac{a - 2b}{3})} \\ {} &= & {(\dfrac{2a + 2b + a - 2b}{3}, \dfrac{a + b - a + 2b}{3})} \\ {} &= & {(\dfrac{3a}{3}, \dfrac{3b}{3})} \\ {} &= & {(a, b).} \end{array}\]
Тому ми. довели, що для кожного існує\((x, y) \in \mathbb{R} \times \mathbb{R}\) таке\((a, b) \in \mathbb{R} \times \mathbb{R}\), що\(f(x, y) = (a, b)\). Це доводить, що функція\(f\) є surjection.
Дослідження та діяльність
- Кусково визначені функції. Ми часто говоримо, що функція є кусково визначеною функцією, якщо вона має різні правила визначення вихідних даних для різних частин своєї області. Наприклад, ми можемо визначити функцію,\(f: \mathbb{R} \to \mathbb{R}\) надавши правило обчислення\(f(x)\) when\(x \ge 0\) та надавши правило для обчислення\(f(x)\) при x < 0 наступним чином:
\[f(x) = \begin{cases} x^2 + 1, & \text{ if \(x\) \(\ge\) 0;} \\ x - 1 & \text{ if \(x\) < 0.} \end{cases}\]
(a) Намалюйте графік функції\(f\). Чи є функція\(f\) і ін'єкція? Чи є функція\(f\) відсмоктування? Обгрунтуйте свої висновки.
Для кожної з наступних функцій визначте, чи є функція ін'єкцією, і визначити, чи є функція surjection. Обгрунтуйте всі висновки.
(б)\(g: [0, 1] \to (0, 1)\) по
\[g(x) = \begin{cases} 0.8, & \text{ if \(x = 0\);} \\ 0.5x & \text{ if \(0 < x < 1\);} \\ 0.6 & \text{ if \(x = 1\).} \end{cases}\]
(с)\(h: \mathbb{Z} \to \{0, 1\}\) шляхом
\[h(x) = \begin{cases} 0, & \text{ if \(x\) is even;} \\ 1, & \text{ if \(x\) is odd.} \end{cases}\] - Функції Домен яких є\(\mathcal{M}_2(\mathbb{R})\). Дозвольте\(\mathcal{M}_2(\mathbb{R})\). представляти множини всіх 2 на 2 матриці над\(\mathbb{R}\).
(а) Визначити це:\(\mathcal{M}_2(\mathbb{R}) \to \mathbb{R}\) по
\ [det
\ left [{\ begin {масив} {cc}
a & b\\
c & d\
\ end {масив}}\ право]
= оголошення - bc.\]
Це є детермінантна функція, введена у вправі (9) з розділу 6.2. Визначальна функція - це ін'єкція? Чи є детермінантна функція відсмоктування? Обгрунтуйте свої висновки.
(б) Визначити тран:\(\mathcal{M}_2(\mathbb{R}) \to \mathcal{M}_2(\mathbb{R})\) по
\ [тран
\ ліворуч [{\ begin {масив} {cc}
a & b\\
c & d\
\ end {масив}}\ справа]
= A^T =
\ left [{\\ begin {array} {cc}
a & c\\
b & d\
\ end {array}}\ right].\]
Це функція транспонування, введена у Вправі (10) з розділу 6.2. Чи є функція транспонування ін'єкцією? Чи є функція транспонування відрижкою? Обгрунтуйте свої висновки.
(c) Визначити\(F: \mathcal{M}_2(\mathbb{R}) \to \mathbb{R}\) за допомогою
\ [F
\ left [{\ begin {масив} {
cc}
a & b\
\ c & d\\ end {масив}}\ справа]
= a^2 + d^2 - c^2.\]
є функція\(F\) ін'єкції? Чи є функція\(F\) відсмоктування? Обгрунтуйте свої висновки.
- Відповідь
-
Додайте сюди тексти. Не видаляйте цей текст спочатку.
