4.12: Додатки
- Page ID
- 63121
Додатки
- Застосовуйте поняття векторів\(\mathbb{R}^n\) у застосуваннях фізики та роботи.
Вектори та фізика
Припустимо, ви натискаєте на щось. Потім ваш поштовх складається з двох компонентів, наскільки сильно ви натискаєте, і напрямок, який ви натискаєте. Це ілюструє поняття сили.
Сила - вектор. Величина цього вектора є мірою того, наскільки сильно він штовхається. Він вимірюється в таких одиницях, як Ньютони або фунти або тонни. Напрямок цього вектора - це напрямок, в якому відбувається поштовх.
Вектори використовуються для моделювання сили та інших фізичних векторів, таких як швидкість. Як і у всіх векторах, сила векторного моделювання має дві основні складові, її величину та напрямок.
Згадайте спеціальні вектори, які вказують уздовж осей координат. Вони задаються тим,\[\vec{e}_{i} = \left [ 0 \cdots 0 \; 1 \; 0 \cdots 0 \right ]^T\nonumber \] де\(1\) знаходиться в\(i^{th}\) слоті і є нулі у всіх інших просторах. Напрямок\(\vec{e}_{i}\) позначається як\(i^{th}\) напрямок.
Розглянемо наступну картину, яка ілюструє випадок\(\mathbb{R}^{3}.\) Recall, що в\(\mathbb{R}^3\), ми можемо посилатися на ці вектори як\(\vec{i}, \vec{j},\) і\(\vec{k}\).
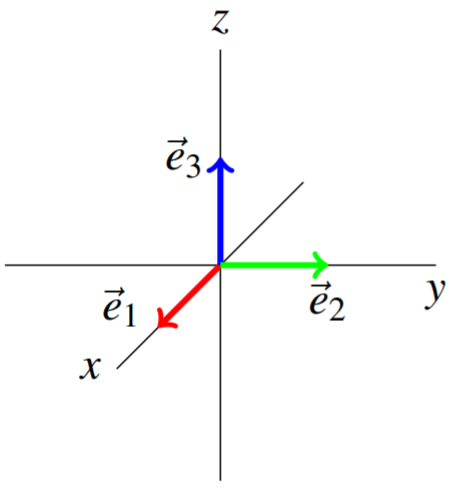
З огляду на вектор\(\vec{u}=\left [ u_{1} \cdots u_{n}\right ]^T ,\) випливає, що\[\vec{u}=u_{1}\vec{e}_{1}+\cdots +u_{n}\vec{e}_{n}= \sum_{k=1}^{n}u_{i}\vec{e}_{i}\nonumber \]
Що означає додавання векторів фізично? Припустимо, до якогось предмету прикладено дві сили. Кожен з них буде представлений вектором сили, і дві сили, що діють разом, дадуть загальну силу, що діє на об'єкт, яка також була б вектором сили, відомим як результуюча. Припустимо, що два вектори є\(\vec{u}=\sum_{k=1}^{n}u_{i}\vec{e}_{i}\) і\(\vec{v}=\sum_{k=1}^{n}v_{i}\vec{e}_{i}\). Тоді вектор\(\vec{u}\) включає компонент у\(i^{th}\) напрямку\(u_{i}\vec{e}_{i}\), заданому, тоді як компонент у\(i^{th}\) напрямку\(\vec{v}\) є\(v_{i}\vec{e}_{i}.\) Тоді вектор\(\vec{u} + \vec{v}\) повинен мати компонент у\(i^{th}\) напрямку рівному\(\left( u_{i}+v_{i}\right) \vec{e}_{i}.\) Це саме те, що є отримані при векторах,\(\vec{u}\) і\(\vec{v}\) додаються. \[\begin{aligned} \vec{u}+\vec{v}& =\left [ u_{1}+v_{1} \cdots u_{n}+v_{n}\right ]^T \\ & =\sum_{i=1}^{n}\left( u_{i}+v_{i}\right) \vec{e}_{i}\end{aligned}\]
Таким чином, додавання векторів за правилами додавання, в\(\mathbb{R }^{n}\) яких були представлені раніше, дає відповідний вектор, який дублює кумулятивний ефект всіх векторів у сумі.
Розглянемо тепер кілька прикладів векторного додавання.
До машини прикріплені три мотузки, і три людини тягнуть за ці мотузки. Перший чинить силу\(\vec{F}_1 = 2\vec{i} + 3\vec{j} -2 \vec{k}\) Ньютонів, другий чинить силу\(\vec{F}_2 = 3\vec{i}+5\vec{j}+\vec{k}\) Ньютонів, а третій надає силу\(5\vec{i}-\vec{j}+2\vec{k}\) Ньютонів. Знайдіть сумарну силу в сторону\(\vec{i}\).
Рішення
Щоб знайти сумарну силу, складаємо вектори, як описано вище. Це дається\[\begin{aligned} &(2\vec{i}+3\vec{j}-2\vec{k}) + (3\vec{i}+5\vec{j}+\vec{k}) + (5\vec{i}-\vec{j}+2\vec{k})\\ &= (2 + 3 + 5) \vec{i} + (3 + 5 + -1) \vec{j} + (-2+1+2) \vec{k} \\ &= 10 \vec{i} + 7 \vec{j} + \vec{k}\end{aligned}\] Отже, загальна сила\(10\vec{i}+7\vec{j}+\vec{k}\) Ньютонів. Тому сила в\(\vec{i}\) напрямку -\(10\) Ньютон.
Розглянемо ще один приклад.
Літак летить на північний схід зі швидкістю 100 миль на годину. Напишіть це як вектор.
Рішення
Далі випливає картина цієї ситуації.
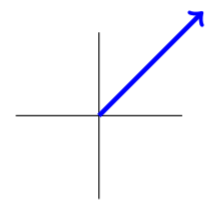
Тому нам потрібно знайти вектор,\(\vec{u}\) який має довжину 100 і напрямок, як показано на цій діаграмі. Вектор можна розглядати\(\vec{u}\) як гіпотенузу прямокутного трикутника, що має рівні сторони, так як напрямок\(\vec{u}\) відповідає\(45 ^{\circ}\) прямій. Сторони, відповідні\(\vec{j}\) напрямку\(\vec{i}\) та, повинні бути кожна довжиною 100/\(\sqrt{2}.\) Отже, вектор задається\[\vec{u} = \frac{100}{\sqrt{2}} \vec{i}+ \frac{100}{\sqrt{2 }}\vec{j} = \left [ \begin{array}{rr} {0.05in} \frac{100}{\sqrt{2}} & {0.05in}\frac{100}{\sqrt{2}} \end{array} \right ]^T \nonumber \]
Цей приклад також мотивує поняття швидкості, визначене нижче.
Швидкість об'єкта - це міра того, наскільки швидко він рухається. Вимірюється в одиницях довжини в одиницю часу. Наприклад, милі на годину, кілометри в хвилину, фути в секунду. Швидкість - це вектор, який має швидкість як величину, але також визначає напрямок.
Таким чином, вектор швидкості в наведеному вище прикладі є\( {0.05in}\frac{100}{\sqrt{2}}\vec{i}+ {0.05in}\frac{100}{\sqrt{2}}\vec{j}\), тоді як швидкість становить\(100\) милі на годину.
Розглянемо наступний приклад.
Швидкість літака\(100\vec{i}+\vec{j}+\vec{k}\) вимірюється в кілометрах на годину і в певний момент часу його положення становить\(\left( 1,2,1\right) .\)
Знайдіть положення цього літака через хвилину.
Рішення
Тут уявіть декартову систему координат, в якій третім компонентом є висота, а перша і друга складові вимірюються на лінії із заходу на схід і лінії з півдня на північ.
Розглянемо вектор\(\left [ \begin{array}{rrr} 1 & 2 & 1 \end{array} \right ]^T ,\), який є початковим вектором положення літака. У міру руху площини вектор положення змінюється відповідно до вектора швидкості. Через одну хвилину (вважається\(\frac{1}{60}\) годиною) літак рухався у\(\vec{i}\) напрямку на відстань в\(100\times \frac{1}{60}= \frac{5}{3}\) кілометр. У\(\vec{j}\) напрямку він перемістився\(\frac{1}{60}\) кілометр за цей же час, при цьому рухається\(\frac{1}{60}\) кілометр у\(\vec{k}\) напрямку. Тому новий вектор переміщення для літака є\[\left [ \begin{array}{rrr} 1 & 2 & 1 \end{array} \right ]^T + \left [ \begin{array}{rrr} \frac{5}{3} & \frac{1}{60} & \frac{1}{60} \end{array} \right ]^T =\left [ \begin{array}{rrr} \frac{8}{3} & \frac{121}{60} & \frac{121}{60} \end{array} \right ]^T\nonumber \]
Тепер розглянемо приклад, який передбачає об'єднання двох швидкостей.
Певна річка шириною півкілометра з течією, що протікає зі сходу на захід зі швидкістю 4 кілометри на годину. Людина пливе прямо до протилежного берега від Південного берега річки зі швидкістю 3 кілометри на годину. Як далеко вниз по річці він опиняється, коли переплив? Як далеко він закінчується плаванням?
Рішення
Розглянемо наступну картину, яка демонструє вищеописаний сценарій.
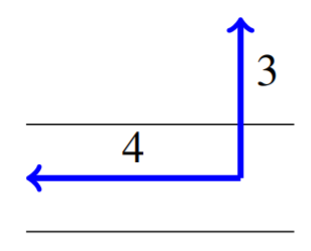
Спочатку ми хочемо дізнатися загальний час запливу через річку. Швидкість у напрямку через річку становить\(3\) кілометри на годину, а ширина річки -\(\frac{1}{2}\) кілометр. Далі поїздка займає\(1/6\) годину або\(10\) хвилини.
Тепер ми можемо обчислити, наскільки далеко вниз за течією він опиниться. Так як річка протікає зі швидкістю\(4\) кілометрів на годину, а поїздка займає\(1/6\) годину, відстань, пройдене нижче за течією, дається\(4 \left(\frac{1}{6}\right) = \frac{2}{3}\) кілометрами.
Відстань, пройдену плавцем, задається гіпотенузою прямокутного трикутника. Дві руки трикутника задаються відстанню через річку,\(\frac{1}{2}\) км, і відстань, пройдену вниз за течією,\(\frac{2}{3}\) км. Потім, використовуючи теорему Піфагора, ми можемо обчислити загальну\(d\) пройдену відстань. \[d = \sqrt{ \left(\frac{2}{3} \right)^2 + \left( \frac{1}{2} \right) ^2 } = \frac{5}{6} \mbox{km}\nonumber \]
Тому плавець долає загальну відстань\(\frac{5}{6}\) кілометрів.
Робота
Математична концепція роботи являє собою застосування векторів в\(\mathbb{R}^n\). Фізичне поняття праці відрізняється від поняття праці, зайнятого в звичайній бесіді. Наприклад, припустимо, що ви повинні були ковзати 150 фунтів ваги від столу, який є три фути висотою і перетасувати вздовж підлоги для 50 ярдів, зберігаючи висоту завжди три фути, а потім внести цю вагу на інший три фути високий стіл. Фізична концепція роботи вказувала б на те, що сила, яку чинили ваші руки, не працювала під час цього проекту. Причина такого визначення полягає в тому, що навіть якщо ваші руки чинили значну силу на вагу, напрямок руху було під прямим кутом до сили, яку вони чинили. Єдина частина сили, яка працює в сенсі фізики, є складовою сили у напрямку руху.
Робота визначається як величина складової цієї сили на відстань, на яку вона діє, коли складова сили вказує у напрямку руху. У разі, коли сила вказує в точності протилежному напрямку руху, робота задається в\(\left( -1\right)\) рази величина цієї складової, що перевищує відстань. Таким чином, робота, виконана силою над об'єктом, коли об'єкт рухається з однієї точки в іншу, є мірою того, наскільки сила сприяє руху. Це проілюстровано на наступній картинці в тому випадку, коли дана сила сприяє руху.
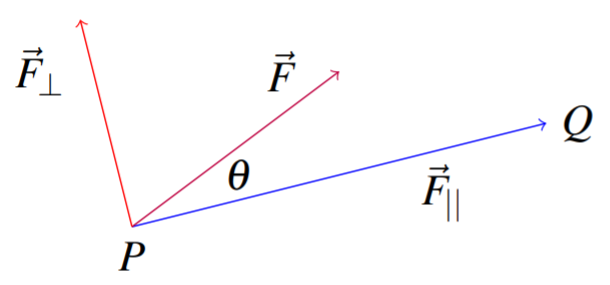
Нагадаємо, що для будь-якого вектора\(\vec{u}\) в\(\mathbb{R}^n\), ми можемо записати\(\vec{u}\) як суму двох векторів, як в\[\vec{u} = \vec{u}_{||} + \vec{u}_{\perp}\nonumber \] Для будь-якої сили\(\vec{F}\), ми можемо записати цю силу як суму вектора в напрямку руху і вектора, перпендикулярного руху. Іншими словами,\[\vec{F} = \vec{F}_{||} + \vec{F}_{\bot}\nonumber \]
На наведеному вище зображенні сила,\(\vec{F}\) прикладається до об'єкта, який рухається по прямій лінії від\(P\) до\(Q.\) Є два вектори показані,\(\vec{F}_{||}\)\(\vec{F}_{\bot }\) і малюнок призначений для того, щоб вказати, що при додаванні цих двох векторів ви отримаєте\(\vec{F}\). Іншими словами,\(\vec{F} = \vec{F}_{||} + \vec{F}_{\bot}\). Зверніть увагу, що\(\vec{F}_{||}\) діє у напрямку руху і\(\vec{F}_{\bot }\) діє перпендикулярно напрямку руху. Тільки\(\vec{F}_{||}\) сприяє виконаній роботою над об'єктом у міру його переміщення від\(P\) до\(Q\).\(\vec{F}\) \(\vec{F}_{||}\)називається складовою сили у напрямку руху. З тригонометрії ви бачите, що величина\(\vec{F}_{||}\) повинна дорівнювати.\( \| \vec{F} \| \left| \cos \theta \right| .\) Таким чином, оскільки\(\vec{F}_{||}\) точки в напрямку вектора від\(P\) до\(Q,\) загальної виконаної роботи повинні дорівнювати\[ \| \vec{F} \| \| \vec{PQ} \| \cos \theta = \| \vec{F} \| \| \vec{q}-\vec{p} \| \cos \theta\nonumber \]
Тепер, припустимо, що включений кут був тупим. Тоді робота, виконана силою\(\vec{F}\) над об'єктом, була б негативною, оскільки\(-1\) вказувала\(\vec{F}_{||}\) б у рази напрямок руху. У цьому випадку також\(\cos \theta\) буде негативним, і тому все ще залишається так, що виконана робота буде дана за вищевказаною формулою. Таким чином, з геометричного опису точкового добутку, наведеного вище, робота дорівнює\[ \| \vec{F} \| \| \vec{q}-\vec{p} \| \cos \theta =\vec{F}\bullet \left( \vec{q}-\vec{p}\right)\nonumber \] Це пояснює наступне визначення.
\(\vec{F}\)Дозволяти сила, що діє на об'єкт, який рухається від точки\(P\) до точки\(Q\), які мають вектори положення, задані\(\vec{q}\) відповідно\(\vec{p}\) і. Тоді робота, виконана над об'єктом за заданою силою, дорівнює\(\vec{F}\bullet \left( \vec{q}-\vec{p}\right) .\)
Розглянемо наступний приклад.
Нехай\(\vec{F}= \left [ \begin{array}{rrr} 2 & 7 & -3 \end{array} \right ]^T\) Ньютони. Знайдіть роботу, виконану цією силою в русі від точки\(\left( 1,2,3\right)\) до точки\(\left( -9,-3,4\right)\) по прямому відрізку, що з'єднує ці точки, де відстані вимірюються в метрах.
Рішення
Спочатку обчислити вектор\(\vec{q} - \vec{p}\), заданий\[\left [ \begin{array}{rrr} -9 & -3 & 4 \end{array} \right ]^T - \left [ \begin{array}{rrr} 1 & 2 & 3 \end{array} \right ]^T = \left [ \begin{array}{rrr} -10 & -5 & 1 \end{array} \right ]^T\nonumber \]
Згідно з \(\PageIndex{3}\)визначенням, виконана робота є\[\begin{aligned} \left [ \begin{array}{rrr} 2 & 7 & 3 \end{array} \right ]^T \bullet \left [ \begin{array}{rrr} -10 & -5 & 1 \end{array} \right ]^T & =-20+\left( -35\right) +\left( -3\right) \\ & =-58\text{ Newton meters}\end{aligned}\]
Зверніть увагу, що якби сила була дана в фунтах, а відстань була дана в ногах, одиниці на роботі були б фунтами ніг. Загалом, робота має одиниці, рівні одиницям сили на одиниці довжини. Нагадаємо, що метр\(1\) Ньютона дорівнює\(1\) Джоулю. Також зверніть увагу, що робота, виконана силою, може бути негативною, як в наведеному вище прикладі.
