4.11: Ортогональність
- Page ID
- 63098
- Визначте, чи є дана множина ортогональною або ортонормальною.
- Визначте, чи є дана матриця ортогональною.
- З огляду на лінійно незалежну множину, скористайтеся процесом Грама-Шмідта, щоб знайти відповідні ортогональні та ортонормальні множини.
- Знайти ортогональну проекцію вектора на підпростір.
- Знайдіть наближення найменших квадратів для набору точок.
У цьому розділі ми розглянемо, що означає, щоб вектори (і набори векторів) були ортогональними та ортонормальними. По-перше, необхідно переглянути деякі важливі поняття. Ви можете згадати визначення для діапазону множини векторів та лінійного незалежного набору векторів. Ми включимо тут визначення та приклади для зручності.
Колекція всіх лінійних комбінацій множини векторів\(\{ \vec{u}_1, \cdots ,\vec{u}_k\}\) в\(\mathbb{R}^{n}\) відома як проміжок цих векторів і записується як\(\mathrm{span} \{\vec{u}_1, \cdots , \vec{u}_k\}\).
Ми називаємо колекцію форми\(\mathrm{span} \{\vec{u}_1, \cdots , \vec{u}_k\}\) підпростором\(\mathbb{R}^{n}\).
Розглянемо наступний приклад.
Опишіть проліт векторів\(\vec{u}=\left[ \begin{array}{rrr} 1 & 1 & 0 \end{array} \right]^T\) і\(\vec{v}=\left[ \begin{array}{rrr} 3 & 2 & 0 \end{array} \right]^T \in \mathbb{R}^{3}\).
Рішення
Ви можете бачити, що будь-яка лінійна комбінація векторів\(\vec{u}\) і\(\vec{v}\) дає вектор\(\left[ \begin{array}{rrr} x & y & 0 \end{array} \right]^T\) в\(XY\) -площині.
Більш того, кожен вектор в\(XY\) -площині насправді є такою лінійною комбінацією векторів\(\vec{u}\) і\(\vec{v}\). Це тому, що\[\left[ \begin{array}{r} x \\ y \\ 0 \end{array} \right] = (-2x+3y) \left[ \begin{array}{r} 1 \\ 1 \\ 0 \end{array} \right] + (x-y)\left[ \begin{array}{r} 3 \\ 2 \\ 0 \end{array} \right]\nonumber \]
Таким чином проліт\(\{\vec{u},\vec{v}\}\) є саме\(XY\) -площиною.
Проміжок набору векторів в\(\mathbb{R}^n\) є те, що ми називаємо підпростором\(\mathbb{R}^n\). Підпростір\(W\) характеризується особливістю того, що будь-яка лінійна комбінація векторів знову ж таки\(W\) є вектором, що міститься в\(W\).
Ще одна важлива властивість множин векторів називається лінійна незалежність.
Безліч ненульових векторів\(\{ \vec{u}_1, \cdots ,\vec{u}_k\}\) в\(\mathbb{R}^{n}\) вважається лінійно незалежним, якщо жоден вектор у цій множині не знаходиться в діапазоні інших векторів цієї множини.
Ось приклад.
Розглянемо вектори\(\vec{u}=\left[ \begin{array}{rrr} 1 & 1 & 0 \end{array} \right]^T\)\(\vec{v}=\left[ \begin{array}{rrr} 3 & 2 & 0 \end{array} \right]^T\), і\(\vec{w}=\left[ \begin{array}{rrr} 4 & 5 & 0 \end{array} \right]^T \in \mathbb{R}^{3}\). Перевірте, чи\(\{\vec{u}, \vec{v}, \vec{w}\}\) є набір лінійно незалежним.
Рішення
Ми вже перевірили в прикладі\(\PageIndex{1}\), що\(\mathrm{span} \{\vec{u}, \vec{v} \}\) є\(XY\) -plane. Оскільки явно також\(\vec{w}\) знаходиться в\(XY\) -площині, то набір\(\{\vec{u}, \vec{v}, \vec{w}\}\) не лінійно незалежний.
З точки зору spanning, набір векторів лінійно незалежний, якщо він не містить непотрібних векторів. У попередньому прикладі ви можете побачити, що вектор\(\vec{w}\) не допомагає охопити будь-який новий вектор, який ще не знаходиться в діапазоні двох інших векторів. Однак ви можете переконатися,\(\{\vec{u}, \vec{v}\}\) що множина лінійно незалежна, оскільки ви не отримаєте\(XY\) -plane як проліт одного вектора.
Ми також можемо визначити, чи є набір векторів лінійно незалежним шляхом вивчення лінійних комбінацій. Набір векторів лінійно незалежний тоді і тільки тоді, коли лінійна комбінація цих векторів дорівнює нулю, з цього випливає, що всі коефіцієнти дорівнюють нулю. Це хороша вправа для перевірки цієї еквівалентності, і ця остання умова часто використовується як (еквівалентне) визначення лінійної незалежності.
Якщо підпростір охоплюється лінійно незалежним набором векторів, то ми говоримо, що він є основою для підпростору.
\(V\)Дозволяти бути підпростором\(\mathbb{R}^{n}\). Тоді\(\left\{ \vec{u}_{1},\cdots ,\vec{u}_{k}\right\}\) є підставою для того,\(V\) якщо дотримуються наступні дві умови.
- \(\mathrm{span}\left\{ \vec{u}_{1},\cdots ,\vec{u}_{k}\right\} =V\)
- \(\left\{ \vec{u}_{1},\cdots ,\vec{u}_{k}\right\}\)лінійно незалежний
Таким чином, множина векторів\(\{\vec{u}, \vec{v}\}\) з Прикладу\(\PageIndex{2}\) є основою для\(XY\) -plane in,\(\mathbb{R}^{3}\) оскільки вона одночасно лінійно незалежна і охоплює\(XY\) -площину.
Нагадаємо з властивостей точкового добутку векторів, що два вектори\(\vec{u}\) і\(\vec{v}\) є ортогональними if\(\vec{u} \cdot \vec{v} = 0\). Припустимо, вектор ортогональний до охоплюючого набору\(\mathbb{R}^n\). Що можна сказати про такий вектор? Це обговорення в наступному прикладі.
Нехай\(\{\vec{x}_1, \vec{x}_2, \ldots, \vec{x}_k\}\in\mathbb{R}^n\) і припустимо\(\mathbb{R}^n=\mathrm{span}\{\vec{x}_1, \vec{x}_2, \ldots, \vec{x}_k\}\). Крім того, припустимо, що існує вектор,\(\vec{u}\in\mathbb{R}^n\) для якого\(\vec{u}\cdot \vec{x}_j=0\) для всіх\(j\),\(1\leq j\leq k\). Який тип вектора буває\(\vec{u}\)?
Рішення
Напишіть\(\vec{u}=t_1\vec{x}_1 + t_2\vec{x}_2 +\cdots +t_k\vec{x}_k\) для деяких\(t_1, t_2, \ldots, t_k\in\mathbb{R}\) (це можливо, тому що\(\vec{x}_1, \vec{x}_2, \ldots, \vec{x}_k\) span\(\mathbb{R}^n\)).
Тоді
\[\begin{aligned} \| \vec{u} \| ^2 & = \vec{u}\cdot\vec{u} \\ & = \vec{u}\cdot(t_1\vec{x}_1 + t_2\vec{x}_2 +\cdots +t_k\vec{x}_k) \\ & = \vec{u}\cdot (t_1\vec{x}_1) + \vec{u}\cdot (t_2\vec{x}_2) + \cdots + \vec{u}\cdot (t_k\vec{x}_k) \\ & = t_1(\vec{u}\cdot \vec{x}_1) + t_2(\vec{u}\cdot \vec{x}_2) + \cdots + t_k(\vec{u}\cdot \vec{x}_k) \\ & = t_1(0) + t_2(0) + \cdots + t_k(0) = 0.\end{aligned}\]
З тих пір\( \| \vec{u} \| ^2 =0\),\( \| \vec{u} \| =0\). Ми знаємо, що\( \| \vec{u} \| =0\) якщо і тільки якщо\(\vec{u}=\vec{0}_n\). Тому,\(\vec{u}=\vec{0}_n\). На закінчення, єдиним вектором, ортогональним до кожного вектора охоплюючої множини,\(\mathbb{R}^n\) є нульовий вектор.
Тепер ми можемо обговорити, що мається на увазі під ортогональним набором векторів.
\(\{ \vec{u}_1, \vec{u}_2, \cdots, \vec{u}_m \}\)Дозволяти бути набір векторів в\(\mathbb{R}^n\). Тоді цей набір називається ортогональним набором, якщо дотримуються такі умови:
- \(\vec{u}_i \cdot \vec{u}_j = 0\)для всіх\(i \neq j\)
- \(\vec{u}_i \neq \vec{0}\)для всіх\(i\)
Якщо ми маємо ортогональний набір векторів і нормалізуємо кожен вектор так, щоб вони мали довжину 1, результуючий набір називається ортонормальним набором векторів. Їх можна описати наступним чином.
Набір векторів, як кажуть,\(\left\{ \vec{w}_{1},\cdots ,\vec{w}_{m}\right\}\) є ортонормальним набором, якщо\[\vec{w}_i \cdot \vec{w}_j = \delta _{ij} = \left\{ \begin{array}{c} 1\text{ if }i=j \\ 0\text{ if }i\neq j \end{array} \right.\nonumber \]
Зауважте, що всі ортонормальні множини є ортогональними, але зворотне не обов'язково вірно, оскільки вектори не можуть бути нормалізовані. Для того щоб нормалізувати вектори, нам просто потрібно розділити кожен на його довжину.
Нормалізація ортогональної множини - це процес перетворення ортогонального (але не ортонормального) набору в ортонормальний набір. Якщо\(\{ \vec{u}_1, \vec{u}_2, \ldots, \vec{u}_k\}\) є ортогональною підмножиною\(\mathbb{R}^n\), то\[\left\{ \frac{1}{ \| \vec{u}_1 \| }\vec{u}_1, \frac{1}{ \| \vec{u}_2 \| }\vec{u}_2, \ldots, \frac{1}{ \| \vec{u}_k \| }\vec{u}_k \right\}\nonumber \] є ортонормальним множиною.
Ми проілюструємо це поняття на наступному прикладі.
Розглянемо набір векторів, заданих\[\left\{ \vec{u}_1, \vec{u}_2 \right\} = \left\{ \left[ \begin{array}{c} 1 \\ 1 \end{array} \right], \left[ \begin{array}{r} -1 \\ 1 \end{array} \right] \right\}\nonumber \] Show, що це ортогональний набір векторів, але не ортонормальний. Знайдіть відповідну ортонормальну множину.
Рішення
Один легко перевіряє, що\(\vec{u}_1 \cdot \vec{u}_2 = 0\) і\(\left\{ \vec{u}_1, \vec{u}_2 \right\}\) є ортогональним набором векторів. З іншого боку, можна обчислити, що\( \| \vec{u}_1 \| = \| \vec{u}_2 \| = \sqrt{2} \neq 1\) і, таким чином, це не ортонормальний набір.
Таким чином, щоб знайти відповідний ортонормальний набір, нам просто потрібно нормалізувати кожен вектор. Напишемо\(\{ \vec{w}_1, \vec{w}_2 \}\) для відповідного ортонормального набору. Потім,\[\begin{aligned} \vec{w}_1 &= \frac{1}{ \| \vec{u}_1 \| } \vec{u}_1\\ &= \frac{1}{\sqrt{2}} \left[ \begin{array}{c} 1 \\ 1 \end{array} \right] \\ &= \left[ \begin{array}{c} \frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}} \end{array} \right]\end{aligned}\]
Аналогічно,\[\begin{aligned} \vec{w}_2 &= \frac{1}{ \| \vec{u}_2 \| } \vec{u}_2\\ &= \frac{1}{\sqrt{2}} \left[ \begin{array}{r} -1 \\ 1 \end{array} \right] \\ &= \left[ \begin{array}{r} -\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}} \end{array} \right]\end{aligned}\]
Тому відповідним ортонормальним набором є\[\left\{ \vec{w}_1, \vec{w}_2 \right\} = \left\{ \left[ \begin{array}{c} \frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}} \end{array} \right], \left[ \begin{array}{r} -\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}} \end{array} \right] \right\}\nonumber \]
Ви можете переконатися, що цей набір є ортогональним.
Розглянемо ортогональний набір векторів в\(\mathbb{R}^n\), написаних\(\{ \vec{w}_1, \cdots, \vec{w}_k \}\) с\(k \leq n\). Проліт цих векторів є\(W\) підпростором\(\mathbb{R}^n\). Якби ми могли показати, що цей ортогональний набір також лінійно незалежний, ми б мали основу\(W\). Ми покажемо це в наступній теоремі.
\(\{ \vec{w}_1, \vec{w}_2, \cdots, \vec{w}_k \}\)Дозволяти бути ортонормальний набір векторів в\(\mathbb{R}^n\). Тоді ця множина лінійно незалежна і утворює основу для підпростору\(W = \mathrm{span} \{ \vec{w}_1, \vec{w}_2, \cdots, \vec{w}_k \}\).
- Доказ
-
Щоб показати, що це лінійно незалежна множина, припустимо, що лінійна комбінація цих векторів дорівнює\(\vec{0}\), наприклад:\[a_1 \vec{w}_1 + a_2 \vec{w}_2 + \cdots + a_k \vec{w}_k = \vec{0}, a_i \in \mathbb{R}\nonumber \] Нам потрібно показати, що все\(a_i = 0\). Для цього візьміть точковий добуток кожної сторони вищевказаного рівняння з вектором\(\vec{w}_i\) і отримайте наступне.
\[\begin{aligned} \vec{w}_i \cdot (a_1 \vec{w}_1 + a_2 \vec{w}_2 + \cdots + a_k \vec{w}_k ) &= \vec{w}_i \cdot \vec{0}\\ a_1 (\vec{w}_i \cdot \vec{w}_1) + a_2 (\vec{w}_i \cdot \vec{w}_2) + \cdots + a_k (\vec{w}_i \cdot \vec{w}_k) &= 0 \end{aligned}\]
Тепер, оскільки набір ортогональний,\(\vec{w}_i \cdot \vec{w}_m = 0\) для всіх\(m \neq i\), так що ми маємо:\[a_1 (0) + \cdots + a_i(\vec{w}_i \cdot \vec{w}_i) + \cdots + a_k (0) = 0\nonumber \]\[a_i \| \vec{w}_i \| ^2 = 0\nonumber \]
Оскільки набір ортогональний, ми це знаємо\( \| \vec{w}_i \| ^2 \neq 0\). Звідси випливає, що\(a_i =0\). Так як\(a_i\) був обраний довільно, набір\(\{ \vec{w}_1, \vec{w}_2, \cdots, \vec{w}_k \}\) лінійно незалежний.
Нарешті\(W = \mbox{span} \{ \vec{w}_1, \vec{w}_2, \cdots, \vec{w}_k \}\), з тих пір, набір векторів також охоплює\(W\) і тому утворює основу\(W\).
Якщо ортогональна множина є основою для підпростору, ми називаємо це ортогональною основою. Аналогічно, якщо ортонормальний набір є основою, ми називаємо це ортонормальною основою.
Завершуємо цей розділ обговоренням розширень Фур'є. З огляду на будь-який ортогональний\(B\) базис\(\mathbb{R}^n\) і довільний вектор\(\vec{x} \in \mathbb{R}^n\), як ми виражаємо\(\vec{x}\) як лінійну комбінацію векторів в\(B\)? Рішення - розширення Фур'є.
\(V\)Дозволяти підпростір\(\mathbb{R}^n\) і припустимо\(\{ \vec{u}_1, \vec{u}_2, \ldots, \vec{u}_m \}\) є ортогональною основою\(V\). Тоді для будь-якого\(\vec{x}\in V\),
\[\vec{x} = \left(\frac{\vec{x}\cdot \vec{u}_1}{ \| \vec{u}_1 \| ^2}\right) \vec{u}_1 + \left(\frac{\vec{x}\cdot \vec{u}_2}{ \| \vec{u}_2 \| ^2}\right) \vec{u}_2 + \cdots + \left(\frac{\vec{x}\cdot \vec{u}_m}{ \| \vec{u}_m \| ^2}\right) \vec{u}_m\nonumber \]
Цей вираз називається розширенням Фур'є\(\vec{x}\), і\[\frac{\vec{x}\cdot \vec{u}_j}{ \| \vec{u}_j \| ^2},\nonumber \]\(j=1,2,\ldots,m\) є коефіцієнтами Фур'є.
Розглянемо наступний приклад.
Нехай\(\vec{u}_1= \left[\begin{array}{r} 1 \\ -1 \\ 2 \end{array}\right], \vec{u}_2= \left[\begin{array}{r} 0 \\ 2 \\ 1 \end{array}\right]\), і\(\vec{u}_3 =\left[\begin{array}{r} 5 \\ 1 \\ -2 \end{array}\right]\), і нехай\(\vec{x} =\left[\begin{array}{r} 1 \\ 1 \\ 1 \end{array}\right]\).
Потім\(B=\{ \vec{u}_1, \vec{u}_2, \vec{u}_3\}\) робиться ортогональна основа\(\mathbb{R}^3\).
Обчислити розширення Фур'є\(\vec{x}\), таким чином\(\vec{x}\) записуючи як лінійну комбінацію векторів\(B\).
Рішення
Так як\(B\) є підставою (перевірити!) існує унікальний спосіб вираження у\(\vec{x}\) вигляді лінійної комбінації векторів\(B\). Більше того\(B\), оскільки є ортогональною основою (перевірити!) , то це можна зробити, обчисливши розширення Фур'є\(\vec{x}\).
Тобто:
\[\vec{x} = \left(\frac{\vec{x}\cdot \vec{u}_1}{ \| \vec{u}_1 \| ^2}\right) \vec{u}_1 + \left(\frac{\vec{x}\cdot \vec{u}_2}{ \| \vec{u}_2 \| ^2}\right) \vec{u}_2 + \left(\frac{\vec{x}\cdot \vec{u}_3}{ \| \vec{u}_3 \| ^2}\right) \vec{u}_3. \nonumber\]
Ми з готовністю обчислюємо:
\[\frac{\vec{x}\cdot\vec{u}_1}{ \| \vec{u}_1 \| ^2} = \frac{2}{6}, \; \frac{\vec{x}\cdot\vec{u}_2}{ \| \vec{u}_2 \| ^2} = \frac{3}{5}, \mbox{ and } \frac{\vec{x}\cdot\vec{u}_3}{ \| \vec{u}_3 \| ^2} = \frac{4}{30}. \nonumber\]
Тому,\[\left[\begin{array}{r} 1 \\ 1 \\ 1 \end{array}\right] = \frac{1}{3}\left[\begin{array}{r} 1 \\ -1 \\ 2 \end{array}\right] +\frac{3}{5}\left[\begin{array}{r} 0 \\ 2 \\ 1 \end{array}\right] +\frac{2}{15}\left[\begin{array}{r} 5 \\ 1 \\ -2 \end{array}\right]. \nonumber\]
Ортогональні матриці
Нагадаємо, що процес пошуку зворотної матриці часто був громіздким. На відміну від цього, було дуже легко взяти транспонування матриці. На щастя для деяких спеціальних матриць, транспонування дорівнює зворотному. Коли\(n \times n\) матриця має всі дійсні записи і її транспонування дорівнює її зворотній, матриця називається ортогональною матрицею.
Точне визначення полягає в наступному.
Реальна\(n\times n\) матриця\(U\) називається ортогональною матрицею, якщо
\[UU^{T}=U^{T}U=I.\nonumber \]
Зверніть увагу, оскільки\(U\) вважається квадратною матрицею, достатньо перевірити лише одне з цих рівностей\(UU^{T}=I\) або\(U^{T}U=I\) утримує, щоб гарантувати, що\(U^T\) це зворотне\(U\).
Розглянемо наступний приклад.
Ортогональна матриця Показати\[U=\left[ \begin{array}{rr} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \end{array} \right]\nonumber \] матрицю ортогональну.
Рішення
Все, що нам потрібно зробити, це перевірити (одне з рівнянь від) вимоги визначення\(\PageIndex{7}\).
\[UU^{T}=\left[ \begin{array}{rr} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \end{array} \right] \left[ \begin{array}{rr} \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \end{array} \right] = \left[ \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right]\nonumber \]
Так як\(UU^{T} = I\), ця матриця ортогональна.
Ось ще один приклад.
Ортогональна\(U=\left[ \begin{array}{rrr} 1 & 0 & 0 \\ 0 & 0 & -1 \\ 0 & -1 & 0 \end{array} \right] .\) матриця Нехай\(U\) ортогональна?
Рішення
Знову ж таки, відповідь так, і це можна перевірити, просто показавши, що\(U^{T}U=I\):
\[\begin{aligned} U^{T}U&=\left[ \begin{array}{rrr} 1 & 0 & 0 \\ 0 & 0 & -1 \\ 0 & -1 & 0 \end{array} \right] ^{T}\left[ \begin{array}{rrr} 1 & 0 & 0 \\ 0 & 0 & -1 \\ 0 & -1 & 0 \end{array} \right] \\ &=\left[ \begin{array}{rrr} 1 & 0 & 0 \\ 0 & 0 & -1 \\ 0 & -1 & 0 \end{array} \right] \left[ \begin{array}{rrr} 1 & 0 & 0 \\ 0 & 0 & -1 \\ 0 & -1 & 0 \end{array} \right] \\ &=\left[ \begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right]\end{aligned}\]
Коли ми говоримо, що\(U\) це ортогонально, ми говоримо\(UU^T=I\), що, це означає, що\[\sum_{j}u_{ij}u_{jk}^{T}=\sum_{j}u_{ij}u_{kj}=\delta _{ik}\nonumber \] де\(\delta _{ij}\) знаходиться символ Кронекера, що визначається\[\delta _{ij}=\left\{ \begin{array}{c} 1 \text{ if }i=j \\ 0\text{ if }i\neq j \end{array} \right.\nonumber \]
У словах, добуток\(i^{th}\) рядка\(U\) з рядком\(k^{th}\) дає\(1\) якщо\(i=k\) і\(0\) якщо Те\(i\neq k.\) ж саме вірно для стовпців, тому що\(U^{T}U=I\) також. Тому,\[\sum_{j}u_{ij}^{T}u_{jk}=\sum_{j}u_{ji}u_{jk}=\delta _{ik}\nonumber \] який говорить про те, що добуток одного стовпця з іншим стовпцем дає,\(1\) якщо два стовпці однакові і\(0\) якщо два стовпці різні.
Більш лаконічно це говорить про те, що якщо\(\vec{u}_{1},\cdots ,\vec{u}_{n}\) є стовпцями\(U,\) ортогональної матриці, то\[\vec{u}_{i}\cdot \vec{u}_{j}=\delta _{ij} = \left\{ \begin{array}{c} 1\text{ if }i=j \\ 0\text{ if }i\neq j \end{array} \right.\nonumber \]
Ми скажемо, що стовпці утворюють ортонормальний набір векторів, причому аналогічно для рядків. Таким чином, матриця є ортогональною, якщо її рядки (або стовпці) утворюють ортонормальний набір векторів. Зверніть увагу, що конвенція полягає в тому, щоб назвати таку матрицю ортогональної, а не ортонормальної (хоча це може мати більше сенсу!).
Рядки\(n \times n\) ортогональної матриці утворюють ортонормальну основу\(\mathbb{R}^n\). Крім того, будь-яка ортонормальна основа\(\mathbb{R}^n\) може бути використана для побудови\(n \times n\) ортогональної матриці.
- Доказ
-
Нагадаємо з теореми\(\PageIndex{1}\), що ортонормальна множина є лінійно незалежною і становить основу для його прольоту. Оскільки рядки\(n \times n\) ортогональної матриці утворюють ортонормальну множину, вони повинні бути лінійно незалежними. Тепер у нас є\(n\) лінійно незалежні вектори, і з цього випливає, що їх проміжок дорівнює\(\mathbb{R}^n\). Тому ці вектори утворюють ортонормальну основу для\(\mathbb{R}^n\).
Припустимо, що тепер у нас є ортонормальна основа для\(\mathbb{R}^n\). Оскільки основа буде містити\(n\) вектори, вони можуть бути використані для побудови\(n \times n\) матриці, причому кожен вектор стає рядком. Тому матриця складається з ортонормальних рядків, що за нашим вище обговоренням означає, що матриця ортогональна. Зверніть увагу, що ми могли б також побудувати матрицю з кожним вектором стає стовпець замість цього, і це знову буде ортогональна матриця. Насправді це просто транспонування попередньої матриці.
Розглянемо наступну пропозицію.
Det Припустимо\(U\) є ортогональною матрицею. Тоді\(\det \left( U\right) = \pm 1.\)
- Доказ
-
Цей результат випливає з властивостей детермінант. Нагадаємо, що для будь-якої матриці\(A\),\(\det(A)^T = \det(A)\). Тепер якщо\(U\) ортогональний, то:\[(\det \left( U\right)) ^{2}=\det \left( U^{T}\right) \det \left( U\right) =\det \left( U^{T}U\right) =\det \left( I\right) =1\nonumber \]
Тому\((\det (U))^2 = 1\) і випливає, що\(\det \left( U\right) = \pm 1\).
Ортогональні матриці діляться на два класи, належні і неправильні. Власні ортогональні матриці - це ті, чиї детермінант дорівнює 1, а неправильні - ті, чиї детермінант дорівнює\(-1\). Причина відмінності полягає в тому, що неправильні ортогональні матриці іноді вважаються не мають фізичного значення. Ці матриці спричиняють зміну орієнтації, яка відповідала б матеріалу, що проходить через себе нефізично. Таким чином, розглядаючи, які системи координат повинні розглядатися в певних додатках, вам потрібно враховувати лише ті, які пов'язані належним ортогональним перетворенням. Геометрично лінійні перетворення, що визначаються власними ортогональними матрицями, відповідають складу обертань.
Закінчуємо цей розділ двома корисними властивостями ортогональних матриць.
Припустимо\(A\) і\(B\) є ортогональними матрицями. Тоді\(AB\) і\(A^{-1}\) обидва існують і є ортогональними.
Рішення
Спочатку оглядаємо продукт\(AB\). \[(AB)(B^TA^T)=A(BB^T)A^T =AA^T=I\nonumber \]Так як\(AB\) квадрат,\(B^TA^T=(AB)^T\) є зворотним\(AB\), так і\(AB\) є оборотним, а\((AB)^{-1}=(AB)^T\) отже,\(AB\) ортогональний.
Далі ми покажемо,\(A^{-1}=A^T\) що також ортогонально. \[(A^{-1})^{-1} = A = (A^T)^{T} =(A^{-1})^{T}\nonumber \]Тому\(A^{-1}\) також ортогональний.
Процес грам-Шмідта
Процес Грама-Шмідта є алгоритмом перетворення множини векторів в ортонормальну множину, що охоплює той самий підпростір, який генерує ту саму колекцію лінійних комбінацій (див. Визначення 9.2.2).
Мета процесу Грама-Шмідта полягає в тому, щоб взяти лінійно незалежний набір векторів і перетворити його в ортонормальний набір з однаковим прольотом. Перша мета полягає в побудові ортогональної множини векторів з однаковим прольотом, оскільки звідти ортонормальну множину можна отримати простим діленням кожного вектора на його довжину.
\(\{ \vec{u}_1,\cdots ,\vec{u}_n \}\)Дозволяти набір лінійно незалежних векторів в\(\mathbb{R}^{n}\).
I: Побудувати новий набір векторів\(\{ \vec{v}_1,\cdots ,\vec{v}_n \}\) наступним чином:\[\begin{array}{ll} \vec{v}_1 & = \vec{u}_1 \\ \vec{v}_{2} & = \vec{u}_{2} - \left( \dfrac{ \vec{u}_2 \cdot \vec{v}_1}{ \| \vec{v}_1 \| ^2} \right) \vec{v}_1\\ \vec{v}_{3} & = \vec{u}_{3} - \left( \dfrac{\vec{u}_3 \cdot \vec{v}_1}{ \| \vec{v}_1 \| ^2} \right) \vec{v}_1 - \left( \dfrac{\vec{u}_3 \cdot \vec{v}_2}{ \| \vec{v}_2 \| ^2} \right) \vec{v}_2\\ \vdots \\ \vec{v}_{n} & = \vec{u}_{n} - \left( \dfrac{\vec{u}_n \cdot \vec{v}_1}{ \| \vec{v}_1 \| ^2} \right) \vec{v}_1 - \left( \dfrac{\vec{u}_n \cdot \vec{v}_2}{ \| \vec{v}_2 \| ^2} \right) \vec{v}_2 - \cdots - \left( \dfrac{\vec{u}_{n} \cdot \vec{v}_{n-1}}{ \| \vec{v}_{n-1} \| ^2} \right) \vec{v}_{n-1} \\ \end{array}\nonumber \]
II: Тепер дозвольте\(\vec{w}_i = \dfrac{\vec{v}_i}{ \| \vec{v}_i \| }\)\(i=1, \cdots ,n\).
Тоді
- \(\left\{ \vec{v}_1, \cdots, \vec{v}_n \right\}\)є ортогональним набором.
- \(\left\{ \vec{w}_1,\cdots , \vec{w}_n \right\}\)є ортонормальним набором.
- \(\mathrm{span}\left\{ \vec{u}_1,\cdots ,\vec{u}_n \right\} = \mathrm{span} \left\{ \vec{v}_1, \cdots, \vec{v}_n \right\} = \mathrm{span}\left\{ \vec{w}_1,\cdots ,\vec{w}_n \right\}\).
Рішення
Повний доказ цього алгоритму виходить за рамки цього матеріалу, однак ось вказівка на аргументи.
Щоб показати, що\(\left\{ \vec{v}_1,\cdots , \vec{v}_n \right\}\) це ортогональний набір, нехай\[a_2 = \dfrac{ \vec{u}_2 \cdot \vec{v}_1}{ \| \vec{v}_1 \| ^2}\nonumber \] тоді:\[\begin{array}{ll} \vec{v}_1 \cdot \vec{v}_2 & = \vec{v}_1 \cdot \left( \vec{u}_2 - a_2 \vec{v}_1 \right) \\ & = \vec{v}_1 \cdot \vec{u}_2 - a_2 (\vec{v}_1 \cdot \vec{v}_1 \\ & = \vec{v}_1 \cdot \vec{u}_2 - \dfrac{ \vec{u}_2 \cdot \vec{v}_1}{ \| \vec{v}_1 \| ^2} \| \vec{v}_1 \| ^2 \\ & = ( \vec{v}_1 \cdot \vec{u}_2 ) - ( \vec{u}_2 \cdot \vec{v}_1 ) =0\\ \end{array}\nonumber \] Тепер, коли ви показали, що\(\{ \vec{v}_1, \vec{v}_2\}\) є ортогональним, використовуйте той самий метод, що і вище, щоб показати,\(\{ \vec{v}_1, \vec{v}_2, \vec{v}_3\}\) що також ортогональний, і так далі.
Тоді подібним чином ви це показуєте\(\mathrm{span}\left\{ \vec{u}_1,\cdots ,\vec{u}_n \right\} = \mathrm{span}\left\{ \vec{v}_1,\cdots ,\vec{v}_n \right\}\).
Нарешті визначення\(\vec{w}_i = \dfrac{\vec{v}_i}{ \| \vec{v}_i \| }\) for\(i=1, \cdots ,n\) не впливає на ортогональність і дає вектори довжини 1, отже, ортонормальна множина. Ви також можете помітити, що це також не впливає на проліт, і доказ буде повним.
Розглянемо наступний приклад.
Розглянемо набір векторів,\(\{\vec{u}_1, \vec{u}_2\}\) наведених як у прикладі\(\PageIndex{1}\). Тобто\[\vec{u}_1=\left[ \begin{array}{r} 1 \\ 1 \\ 0 \end{array} \right], \vec{u}_2=\left[ \begin{array}{r} 3 \\ 2 \\ 0 \end{array} \right] \in \mathbb{R}^{3}\nonumber \]
Використовуйте алгоритм Грама-Шмідта, щоб знайти ортонормальний набір векторів,\(\{\vec{w}_1, \vec{w}_2\}\) що мають однаковий проміжок.
Рішення
Ми вже зазначали, що набір векторів в\(\{\vec{u}_1, \vec{u}_2\}\) лінійно незалежний, тому ми можемо приступати до алгоритму Грама-Шмідта:\[\begin{aligned} \vec{v}_1 &= \vec{u}_1 = \left[ \begin{array}{r} 1 \\ 1 \\ 0 \end{array} \right] \\ \vec{v}_{2} &= \vec{u}_{2} - \left( \dfrac{\vec{u}_2 \cdot \vec{v}_1}{ \| \vec{v}_1 \| ^2} \right) \vec{v}_1\\ &= \left[ \begin{array}{r} 3 \\ 2 \\ 0 \end{array} \right] - \frac{5}{2} \left[ \begin{array}{r} 1 \\ 1 \\ 0 \end{array} \right] \\ &= \left[ \begin{array}{r} \frac{1}{2} \\ - \frac{1}{2} \\ 0 \end{array} \right] \end{aligned}\]
Тепер нормалізувати просто нехай\[\begin{aligned} \vec{w}_1 &= \frac{\vec{v}_1}{ \| \vec{v}_1 \| } = \left[ \begin{array}{r} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \\ 0 \end{array} \right] \\ \vec{w}_2 &= \frac{\vec{v}_2}{ \| \vec{v}_2 \| } = \left[ \begin{array}{r} \frac{1}{\sqrt{2}} \\ - \frac{1}{\sqrt{2}} \\ 0 \end{array} \right]\end{aligned}\]
Ви можете перевірити, що\(\{\vec{w}_1, \vec{w}_2\}\) це ортонормальний набір векторів, що мають такий же проміжок\(\{\vec{u}_1, \vec{u}_2\}\), а саме\(XY\) -plane.
У цьому прикладі ми почали з лінійно незалежної множини і знайшли ортонормальний набір векторів, які мали однаковий проміжок. Виходить, що якщо почати з основи підпростору і застосувати алгоритм Грама-Шмідта, то результатом буде ортогональна основа того ж підпростору. Ми розглянемо це в наступному прикладі.
Нехай\[\vec{x}_1=\left[\begin{array}{c} 1\\ 0\\ 1\\ 0 \end{array}\right], \vec{x}_2=\left[\begin{array}{c} 1\\ 0\\ 1\\ 1 \end{array}\right], \mbox{ and } \vec{x}_3=\left[\begin{array}{c} 1\\ 1\\ 0\\ 0 \end{array}\right],\nonumber \] і нехай\(U=\mathrm{span}\{\vec{x}_1, \vec{x}_2,\vec{x}_3\}\). Скористайтеся процесом Грама-Шмідта для побудови\(B\) ортогональної основи\(U\).
Рішення
Перший\(\vec{f}_1=\vec{x}_1\).
Далі,\[\vec{f}_2=\left[\begin{array}{c} 1\\ 0\\ 1\\ 1 \end{array}\right] -\frac{2}{2}\left[\begin{array}{c} 1\\ 0\\ 1\\ 0 \end{array}\right] =\left[\begin{array}{c} 0\\ 0\\ 0\\ 1 \end{array}\right].\nonumber \]
Нарешті,\[\vec{f}_3=\left[\begin{array}{c} 1\\ 1\\ 0\\ 0 \end{array}\right] -\frac{1}{2}\left[\begin{array}{c} 1\\ 0\\ 1\\ 0 \end{array}\right] -\frac{0}{1}\left[\begin{array}{c} 0\\ 0\\ 0\\ 1 \end{array}\right] =\left[\begin{array}{c} 1/2\\ 1\\ -1/2\\ 0 \end{array}\right].\nonumber \]
Тому\[\left\{ \left[\begin{array}{c} 1\\ 0\\ 1\\ 0 \end{array}\right], \left[\begin{array}{c} 0\\ 0\\ 0\\ 1 \end{array}\right], \left[\begin{array}{c} 1/2\\ 1\\ -1/2\\ 0 \end{array}\right] \right\}\nonumber \] є ортогональною основою\(U\). Однак іноді зручніше мати справу з векторами, що мають цілі записи, в цьому випадку ми беремо\[B=\left\{ \left[\begin{array}{c} 1\\ 0\\ 1\\ 0 \end{array}\right], \left[\begin{array}{c} 0\\ 0\\ 0\\ 1 \end{array}\right], \left[\begin{array}{r} 1\\ 2\\ -1\\ 0 \end{array}\right] \right\}.\nonumber \]
Ортогональні проекції
Важливе використання процесу Грама-Шмідта полягає в ортогональних проекціях, фокусі цього розділу.
Ви можете згадати, що підпростір\(\mathbb{R}^n\) - це набір векторів, який містить нульовий вектор і закривається при додаванні і скалярному множенні. Назвемо такий підпростір\(W\). Зокрема, площина, в\(\mathbb{R}^n\) якій міститься походження\(\left(0,0, \cdots, 0 \right)\), є підпростором\(\mathbb{R}^n\).
Припустимо, точка\(Y\) в не\(\mathbb{R}^n\) міститься в\(W\), то яка точка\(Z\) в\(W\) найближчому\(Y\)? Використовуючи процес Грама-Шмідта, ми можемо знайти таку точку. \(\vec{y}, \vec{z}\)Дозволяти представляти вектори положення точок\(Y\) і\(Z\) відповідно, з\(\vec{y}-\vec{z}\) представленням вектора, що з'єднує дві точки\(Y\) і\(Z\). Звідси випливає,\(Z\) що якщо точка на\(W\) найближче до\(Y\), то\(\vec{y} - \vec{z}\) буде перпендикулярно\(W\) (ви бачите, чому?) ; іншими словами,\(\vec{y} - \vec{z}\) ортогональний\(W\) (і до кожного вектора, що міститься в\(W\)), як на наступній діаграмі.
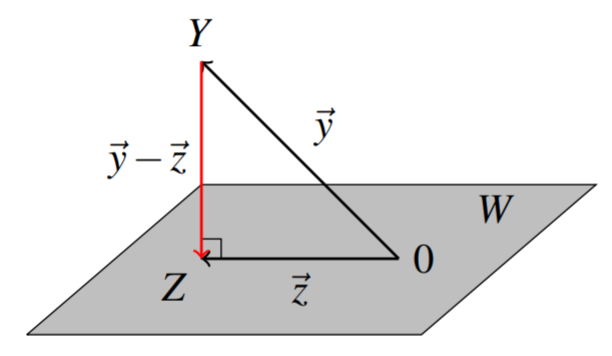
Вектор\(\vec{z}\) називається ортогональної проекцією\(\vec{y}\) на\(W\). Визначення дається наступним чином.
\(W\)Дозволяти бути підпростором\(\mathbb{R}^n\), і\(Y\) бути будь-якою точкою в\(\mathbb{R}^n\). Тоді ортогональна проекція\(Y\) на\(W\) задається тим\[\vec{z} = \mathrm{proj}_{W}\left( \vec{y}\right) = \left( \frac{\vec{y} \cdot \vec{w}_1}{ \| \vec{w}_1 \| ^2}\right) \vec{w}_1 + \left( \frac{\vec{y} \cdot \vec{w}_2}{ \| \vec{w}_2 \| ^2}\right) \vec{w}_2 + \cdots + \left( \frac{\vec{y} \cdot \vec{w}_m}{ \| \vec{w}_m \| ^2}\right) \vec{w}_m\nonumber \], де\(\{\vec{w}_1, \vec{w}_2, \cdots, \vec{w}_m \}\) будь-яка ортогональна основа\(W\).
Тому, щоб знайти ортогональну проекцію, ми повинні спочатку знайти ортогональну основу для підпростору. Зауважте, що можна використовувати ортонормальну основу, але це не обов'язково в цьому випадку, оскільки, як ви можете бачити вище, нормалізація кожного вектора включена у формулу проекції.
Перш ніж ми досліджуємо це далі на прикладі, ми покажемо, що ортогональна проекція дійсно дає точку\(Z\) (точку, вектор положення якої є вектором\(\vec{z}\) вище), яка є точкою\(W\) найближчого до\(Y\).
\(W\)Дозволяти бути підпростором\(\mathbb{R}^n\) і\(Y\) будь-якої точки в\(\mathbb{R}^n\). \(Z\)Дозволяти точка, вектор положення якої ортогональна проекція\(Y\) на\(W\).
Тоді,\(Z\) це точка в\(W\) найближчому до\(Y\).
- Доказ
-
По-перше\(Z\), це, безумовно, точка в\(W\) тому що він знаходиться в прольоті основи\(W\).
Щоб показати, що\(Z\) це точка\(W\) найближче до\(Y\), ми хочемо показати, що\(|\vec{y}-\vec{z}_1| > |\vec{y}-\vec{z}|\) для всіх\(\vec{z}_1 \neq \vec{z} \in W\). Починаємо з написання\(\vec{y}-\vec{z}_1 = (\vec{y} - \vec{z}) + (\vec{z} - \vec{z}_1)\). Тепер вектор\(\vec{y} - \vec{z}\) ортогональний\(W\), і\(\vec{z} - \vec{z}_1\) міститься в\(W\). Тому ці вектори ортогональні один одному. За теоремою Піфагора, ми маємо, що\[ \| \vec{y} - \vec{z}_1 \| ^2 = \| \vec{y} - \vec{z} \| ^2 + \| \vec{z} -\vec{z}_1 \| ^2 > \| \vec{y} - \vec{z} \| ^2\nonumber \] Це випливає, тому що\(\vec{z} \neq \vec{z}_1\) так\( \| \vec{z} -\vec{z}_1 \| ^2 > 0.\)
Отже,\( \| \vec{y} - \vec{z}_1 \| ^2 > \| \vec{y} - \vec{z} \| ^2\). Взявши квадратний корінь з кожного боку, отримуємо бажаний результат.
Розглянемо наступний приклад.
\(W\)Дозволяти площині через початок, заданий рівнянням\(x - 2y + z = 0\). Знайдіть точку в\(W\) найближчій до точки\(Y = (1,0,3)\).
Рішення
Потрібно спочатку знайти ортогональну основу для\(W\). Зверніть увагу, що\(W\) характеризується всіма пунктами\((a,b,c)\) де\(c = 2b-a\). Іншими словами,\[W = \left[ \begin{array}{c} a \\ b \\ 2b - a \end{array} \right] = a \left[ \begin{array}{c} 1 \\ 0 \\ -1 \end{array} \right] + b \left[ \begin{array}{c} 0 \\ 1 \\ 2 \end{array} \right], \; a,b \in \mathbb{R}\nonumber \]
Таким чином, ми можемо писати\(W\) як\[\begin{aligned} W &= \mbox{span} \left\{ \vec{u}_1, \vec{u}_2 \right\} \\ &= \mbox{span} \left\{ \left[ \begin{array}{r} 1 \\ 0 \\ -1 \end{array} \right], \left[ \begin{array}{c} 0 \\ 1 \\ 2 \end{array} \right] \right\}\end{aligned}\]
Зверніть увагу, що цей проміжок є основою\(W\), оскільки він лінійно незалежний. Ми будемо використовувати процес Грама-Шмідта, щоб перетворити це на ортогональну основу,\(\left\{\vec{w}_1, \vec{w}_2 \right\}\). У цьому випадку, як ми помітили, необхідно лише знайти ортогональну основу, і не потрібно, щоб вона була ортонормальною.
\[\vec{w}_1 = \vec{u}_1 = \left[ \begin{array}{r} 1 \\ 0 \\ -1 \end{array} \right]\nonumber \]\[\begin{aligned} \vec{w}_2 &= \vec{u}_2 - \left( \frac{ \vec{u}_2 \cdot \vec{w}_1}{ \| \vec{w}_1 \| ^2} \right) \vec{w}_1\\ &= \left[ \begin{array}{c} 0 \\ 1 \\ 2 \end{array} \right] - \left( \frac{-2}{2}\right) \left[ \begin{array}{r} 1 \\ 0 \\ -1 \end{array} \right] \\ &= \left[ \begin{array}{c} 0 \\ 1 \\ 2 \end{array} \right] + \left[ \begin{array}{r} 1 \\ 0 \\ -1 \end{array} \right] \\ &= \left[ \begin{array}{c} 1 \\ 1 \\ 1 \end{array} \right]\end{aligned}\]
Тому ортогональною основою\(W\) є\[\left\{ \vec{w}_1, \vec{w}_2 \right\} = \left\{ \left[ \begin{array}{r} 1 \\ 0 \\ -1 \end{array} \right], \left[ \begin{array}{c} 1 \\ 1 \\ 1 \end{array} \right] \right\}\nonumber \]
Тепер ми можемо використовувати цю основу, щоб знайти ортогональну проекцію точки\(Y=(1,0,3)\) на підпросторі\(W\). Ми напишемо вектор\(\vec{y}\) позиції\(Y\) як\(\vec{y} = \left[ \begin{array}{c} 1 \\ 0 \\ 3 \end{array} \right]\). Використовуючи Definition\(\PageIndex{8}\), обчислюємо проекцію наступним чином:\[\begin{aligned} \vec{z} &= \mathrm{proj}_{W}\left( \vec{y}\right)\\ &= \left( \frac{\vec{y} \cdot \vec{w}_1}{ \| \vec{w}_1 \| ^2}\right) \vec{w}_1 + \left( \frac{\vec{y} \cdot \vec{w}_2}{ \| \vec{w}_2 \| ^2}\right) \vec{w}_2 \\ &= \left( \frac{-2}{2} \right) \left[ \begin{array}{r} 1 \\ 0 \\ -1 \end{array} \right] + \left( \frac{4}{3} \right) \left[ \begin{array}{c} 1 \\ 1 \\ 1 \end{array} \right] \\ &= \left[ \begin{array}{c} \frac{1}{3} \\ \frac{4}{3} \\ \frac{7}{3} \end{array} \right]\end{aligned}\]
Тому точка\(Z\) на\(W\) найближчій до точки\((1,0,3)\) є\(\left( \frac{1}{3}, \frac{4}{3}, \frac{7}{3} \right)\).
Нагадаємо, що вектор\(\vec{y} - \vec{z}\) перпендикулярний (ортогональний) всім векторам, що містяться в площині\(W\). Використовуючи основу для\(W\), ми можемо знайти всі такі вектори, які перпендикулярні\(W\). Ми називаємо цей набір векторів ортогональним доповненням\(W\) і позначимо його\(W^{\perp}\).
\(W\)Дозволяти бути підпростором\(\mathbb{R}^n\). Тоді ортогональне доповнення\(W\), написане\(W^{\perp}\), є сукупністю всіх векторів,\(\vec{x}\) таких, що\(\vec{x} \cdot \vec{z} = 0\) для всіх векторів\(\vec{z}\) в\(W\). \[W^{\perp} = \{ \vec{x} \in \mathbb{R}^n \; \mbox{such that} \; \vec{x} \cdot \vec{z} = 0 \; \mbox{for all} \; \vec{z} \in W \}\nonumber \]
Ортогональне доповнення визначається як набір усіх векторів, які є ортогональними до всіх векторів у вихідному підпросторі. Виявляється, достатньо, щоб вектори в ортогональному доповненні були ортогональними до охоплюючого набору вихідного простору.
\(W\)Дозволяти бути підпростір\(\mathbb{R}^n\) такого, що\(W = \mathrm{span} \left\{ \vec{w}_1, \vec{w}_2, \cdots, \vec{w}_m \right\}\). Потім\(W^{\perp}\) - набір усіх векторів, які ортогональні кожному з них\(\vec{w}_i\) у наборі.
Наступна пропозиція демонструє, що ортогональне доповнення підпростору сам по собі є підпростором.
\(W\)Дозволяти бути підпростором\(\mathbb{R}^n\). Тоді\(W^{\perp}\) ортогональне доповнення також є підпростором\(\mathbb{R}^n\).
Розглянемо наступну пропозицію.
Доповненням\(\mathbb{R}^n\) є множина, що містить нульовий вектор:\[(\mathbb{R}^n)^{\perp} = \left\{ \vec{0} \right\}\nonumber \] Аналогічно,\[\left\{ \vec{0} \right\}^{\perp} = (\mathbb{R}^n). \nonumber \]
- Доказ
-
Тут\(\vec{0}\) нульовий вектор\(\mathbb{R}^n\). Так як\(\vec{x}\cdot\vec{0}=0\) для всіх\(\vec{x}\in\mathbb{R}^n\),\(\mathbb{R}^n\subseteq\{ \vec{0}\}^{\perp}\). Так як\(\{ \vec{0}\}^{\perp}\subseteq\mathbb{R}^n\), слід рівність, т\(\{ \vec{0}\}^{\perp}=\mathbb{R}^n\). Е.
Знову ж таки, так як\(\vec{x}\cdot\vec{0}=0\) для всіх\(\vec{x}\in\mathbb{R}^n\)\(\vec{0}\in (\mathbb{R}^n)^{\perp}\), так\(\{ \vec{0}\}\subseteq(\mathbb{R}^n)^{\perp}\). Припустимо\(\vec{x}\in\mathbb{R}^n\),\(\vec{x}\neq\vec{0}\). Так як\(\vec{x}\cdot\vec{x}=||\vec{x}||^2\) і\(\vec{x}\neq\vec{0}\)\(\vec{x}\cdot\vec{x}\neq 0\), так\(\vec{x}\not\in(\mathbb{R}^n)^{\perp}\). \((\mathbb{R}^n)^{\perp}\subseteq \{\vec{0}\}\)Тому і таким чином\((\mathbb{R}^n)^{\perp}=\{\vec{0}\}\).
У наступному прикладі ми розглянемо, як знайти\(W^{\perp}\).
\(W\)Дозволяти площині через початок, заданий рівнянням\(x - 2y + z = 0\). Знайдіть основу для ортогонального доповнення\(W\).
Рішення
З Прикладу\(\PageIndex{11}\) ми знаємо, що ми можемо писати\(W\) як\[W = \mbox{span} \left\{ \vec{u}_1, \vec{u}_2 \right\} = \mbox{span} \left\{ \left[ \begin{array}{r} 1 \\ 0 \\ -1 \end{array} \right], \left[ \begin{array}{c} 0 \\ 1 \\ 2 \end{array} \right] \right\}\nonumber \]
Для того, щоб знайти\(W^{\perp}\), нам потрібно знайти всі,\(\vec{x}\) які є ортогональними до кожного вектора в цьому проміжку.
Нехай\(\vec{x} = \left[ \begin{array}{c} x_1 \\ x_2 \\ x_3 \end{array} \right]\). Для того, щоб задовольнити\(\vec{x} \cdot \vec{u}_1 = 0\), має триматися наступне рівняння. \[x_1 - x_3 = 0\nonumber \]
Для того, щоб задовольнити\(\vec{x} \cdot \vec{u}_2 = 0\), має триматися наступне рівняння. \[x_2 + 2x_3 = 0\nonumber \]
Обидва ці рівняння повинні бути задоволені, тому ми маємо наступну систему рівнянь. \[\begin{array}{c} x_1 - x_3 = 0 \\ x_2 + 2x_3 = 0 \end{array}\nonumber \]
Щоб вирішити, налаштуйте доповнену матрицю.
\[\left[ \begin{array}{rrr|r} 1 & 0 & -1 & 0 \\ 0 & 1 & 2 & 0 \end{array} \right]\nonumber \]
Використовуючи гаусову ліквідацію, ми знаходимо\(W^{\perp} = \mbox{span} \left\{ \left[ \begin{array}{r} 1 \\ -2 \\ 1 \end{array} \right] \right\}\), що, а отже,\(\left\{ \left[ \begin{array}{r} 1 \\ -2 \\ 1 \end{array} \right] \right\}\) є основою для\(W^{\perp}\).
Наступні результати узагальнюють важливі властивості ортогональної проекції.
\(W\)Дозволяти бути підпростором\(\mathbb{R}^n\),\(Y\) бути будь-якою точкою в\(\mathbb{R}^n\), і\(Z\) нехай точка в\(W\) найближчому до\(Y\). Потім,
- Вектор\(\vec{z}\) положення точки\(Z\) задається\(\vec{z} = \mathrm{proj}_{W}\left( \vec{y}\right)\)
- \(\vec{z} \in W\)і\(\vec{y} - \vec{z} \in W^{\perp}\)
- \(| Y - Z | < | Y - Z_1 |\)для всіх\(Z_1 \neq Z \in W\)
Розглянемо наступний приклад цього поняття.
Нехай\[\vec{x}_1=\left[\begin{array}{c} 1\\ 0\\ 1\\ 0 \end{array}\right], \vec{x}_2=\left[\begin{array}{c} 1\\ 0\\ 1\\ 1 \end{array}\right], \vec{x}_3=\left[\begin{array}{c} 1\\ 1\\ 0\\ 0 \end{array}\right], \mbox{ and } \vec{v}=\left[\begin{array}{c} 4\\ 3\\ -2\\ 5 \end{array}\right].\nonumber \] Ми хочемо, щоб знайти вектор в\(W =\mathrm{span}\{\vec{x}_1, \vec{x}_2,\vec{x}_3\}\) найближчому до\(\vec{y}\).
Рішення
Спочатку ми будемо використовувати процес Грама-Шмідта для побудови ортогональної основи\(B\), з\(W\):\[B=\left\{ \left[\begin{array}{c} 1\\ 0\\ 1\\ 0 \end{array}\right], \left[\begin{array}{c} 0\\ 0\\ 0\\ 1 \end{array}\right], \left[\begin{array}{r} 1\\ 2\\ -1\\ 0 \end{array}\right] \right\}.\nonumber \]
За теоремою\(\PageIndex{4}\),\[\mathrm{proj}_U(\vec{v}) = \frac{2}{2} \left[\begin{array}{c} 1\\ 0\\ 1\\ 0 \end{array}\right] + \frac{5}{1}\left[\begin{array}{c} 0\\ 0\\ 0\\ 1 \end{array}\right] + \frac{12}{6}\left[\begin{array}{r} 1\\ 2\\ -1\\ 0 \end{array}\right] = \left[\begin{array}{r} 3\\ 4\\ -1\\ 5 \end{array}\right]\nonumber \] це вектор в\(U\) найближчому до\(\vec{y}\).
Розглянемо наступний приклад.
\(W\)Дозволяти підпростір\(W = \mbox{span} \left\{ \left[ \begin{array}{c} 1 \\ 0 \\ 1 \\ 0 \\ \end{array} \right], \left[ \begin{array}{c} 0 \\ 1 \\ 0 \\ 2 \\ \end{array} \right] \right\}\), заданий, і\(Y = (1,2,3,4)\).
Знайдіть точку\(Z\) в\(W\) найближчій до\(Y\), і, крім того, запишіть\(\vec{y}\) як суму вектора в\(W\) і вектора в\(W^{\perp}\).
Рішення
З теореми\(\PageIndex{3}\) точка\(Z\) в\(W\) найближчому до\(Y\) задається\(\vec{z} = \mathrm{proj}_{W}\left( \vec{y}\right)\).
Зверніть увагу, що оскільки наведені вище вектори вже дають ортогональну основу для\(W\), ми маємо:
\[\begin{aligned} \vec{z} &= \mathrm{proj}_{W}\left( \vec{y}\right)\\ &= \left( \frac{\vec{y} \cdot \vec{w}_1}{ \| \vec{w}_1 \| ^2}\right) \vec{w}_1 + \left( \frac{\vec{y} \cdot \vec{w}_2}{ \| \vec{w}_2 \| ^2}\right) \vec{w}_2 \\ &= \left( \frac{4}{2} \right) \left[ \begin{array}{c} 1 \\ 0 \\ 1 \\ 0 \end{array} \right] + \left( \frac{10}{5} \right) \left[ \begin{array}{c} 0 \\ 1 \\ 0 \\ 2 \end{array} \right] \\ &= \left[ \begin{array}{c} 2 \\ 2 \\ 2 \\ 4 \end{array} \right]\end{aligned}\]
Тому точка в\(W\) найближчому до\(Y\) є\(Z = (2,2,2,4)\).
Тепер нам потрібно записати\(\vec{y}\) як суму вектора в\(W\) і вектора в\(W^{\perp}\). Це можна легко зробити наступним чином:\[\vec{y} = \vec{z} + (\vec{y} - \vec{z})\nonumber \] так як\(\vec{z}\) знаходиться в\(W\) і як ми бачили\(\vec{y} - \vec{z}\) в\(W^{\perp}\).
Вектор\(\vec{y} - \vec{z}\) задається\[\vec{y} - \vec{z} = \left[ \begin{array}{c} 1 \\ 2 \\ 3 \\ 4 \end{array} \right] - \left[ \begin{array}{c} 2 \\ 2 \\ 2 \\ 4 \end{array} \right] = \left[ \begin{array}{r} -1 \\ 0 \\ 1 \\ 0 \end{array} \right]\nonumber \] Таким чином, ми можемо записати\(\vec{y}\) як\[\left[ \begin{array}{c} 1 \\ 2 \\ 3 \\ 4 \end{array} \right] = \left[ \begin{array}{c} 2 \\ 2 \\ 2 \\ 4 \end{array} \right] + \left[ \begin{array}{r} -1 \\ 0 \\ 1 \\ 0 \end{array} \right]\nonumber \]
Знайдіть точку\(Z\) в площині\(3x+y-2z=0\), яка найближча до точки\(Y=(1,1,1)\).
Рішення
Розчин буде діяти наступним чином.
- Знайти основу\(X\) підпростору,\(W\)\(\mathbb{R}^3\) визначеного рівнянням\(3x+y-2z=0\).
- Ортогоналізуйте основу,\(X\) щоб отримати\(B\) ортогональну основу\(W\).
- Знайти\(W\) проекцію на вектора положення точки\(Y\).
Тепер приступаємо до вирішення.
- \(3x+y-2z=0\)являє собою систему одного рівняння в трьох змінних. Покладання доповненої матриці в зменшеному рядно-ешелоновому вигляді:\[\left[\begin{array}{rrr|r} 3 & 1 & -2 & 0 \end{array}\right] \rightarrow \left[\begin{array}{rrr|r} 1 & \frac{1}{3} & -\frac{2}{3} & 0 \end{array}\right]\nonumber \] дає загальне рішення\(x=\frac{1}{3}s+\frac{2}{3}t\)\(y=s\),\(z=t\) для будь-якого\(s,t\in\mathbb{R}\). Тоді\[W=\mathrm{span} \left\{ \left[\begin{array}{r} -\frac{1}{3} \\ 1 \\ 0 \end{array}\right], \left[\begin{array}{r} \frac{2}{3} \\ 0 \\ 1 \end{array}\right]\right\}\nonumber \] нехай\(X=\left\{ \left[\begin{array}{r} -1 \\ 3 \\ 0 \end{array}\right], \left[\begin{array}{r} 2 \\ 0 \\ 3 \end{array}\right]\right\}\). Тоді\(X\) є лінійно незалежним і\(\mathrm{span}(X)=W\), таким чином,\(X\) є основою\(W\).
- Використовуйте процес Грама-Шмідта, щоб отримати ортогональну основу\(W\):\[\vec{f}_1=\left[\begin{array}{r} -1\\3\\0\end{array}\right]\mbox{ and }\vec{f}_2=\left[\begin{array}{r}2\\0\\3\end{array}\right]-\frac{-2}{10}\left[\begin{array}{r}-1\\3\\0\end{array}\right]=\frac{1}{5}\left[\begin{array}{r}9\\3\\15\end{array}\right].\nonumber\] Тому\(B=\left\{\left[\begin{array}{r}-1\\3\\0\end{array}\right], \left[\begin{array}{r}3\\1\\5 \end{array}\right]\right\}\) є ортогональною основою\(W\).
- Щоб знайти точку\(Z\) на\(W\) найближчому до\(Y=(1,1,1)\), обчислити\[\begin{aligned} \mathrm{proj}_{W}\left[\begin{array}{r} 1 \\ 1 \\ 1 \end{array}\right] & = \frac{2}{10} \left[\begin{array}{r} -1 \\ 3 \\ 0 \end{array}\right] + \frac{9}{35}\left[\begin{array}{r} 3 \\ 1 \\ 5 \end{array}\right]\\ & = \frac{1}{7}\left[\begin{array}{r} 4 \\ 6 \\ 9 \end{array}\right].\end{aligned}\] Тому,\(Z=\left( \frac{4}{7}, \frac{6}{7}, \frac{9}{7}\right)\).
Наближення найменших квадратів
Не повинно бути дивно чути, що багато проблем не мають ідеального рішення, і в цих випадках мета завжди полягає в тому, щоб намагатися зробити найкраще. Наприклад, що робити, якщо немає розв'язків системи лінійних рівнянь\(A\vec{x}=\vec{b}\)? Виявляється, що те, що ми робимо, - це знаходимо\(\vec{x}\)\(A\vec{x}\) таке, що\(\vec{b}\) максимально наближено до. Дуже важливою технікою, яка випливає з ортогональних проекцій, є найменш квадратна апроксимація, і дозволяє нам робити саме це.
Починаємо з леми.
Нагадаємо, що ми можемо сформувати зображення\(m \times n\) матриці\(A\) по\(\mathrm{im}\left( A\right) = = \left\{ A\vec{x} : \vec{x} \in \mathbb{R}^n \right\}\). Теорема перефразування з\(\PageIndex{4}\) використанням підпростору\(W=\mathrm{im}\left( A\right)\) дає еквівалентність умови ортогональності з умовою мінімізації. Наступна картина ілюструє цю умову ортогональності та геометричне значення цієї теореми.
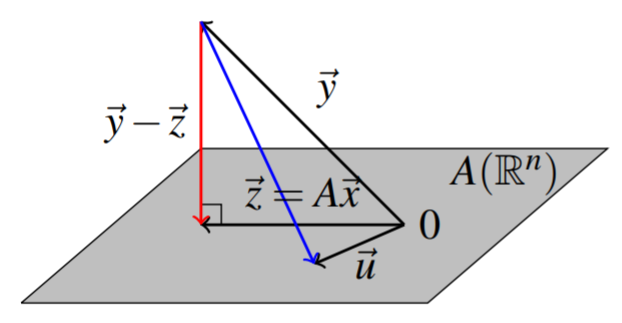
Нехай\(\vec{y}\in \mathbb{R}^{m}\) і нехай\(A\) буде\(m\times n\) матриця.
Вибирайте\(\vec{z}\in W= \mathrm{im}\left( A\right)\) дано\(\vec{z} = \mathrm{proj}_{W}\left( \vec{y}\right)\), і нехай\(\vec{x} \in \mathbb{R}^{n}\) таке\(\vec{z}=A\vec{x}\).
Тоді
- \(\vec{y} - A\vec{x} \in W^{\perp}\)
- \( \| \vec{y} - A\vec{x} \| < \| \vec{y} - \vec{u} \| \)для всіх\(\vec{u} \neq \vec{z} \in W\)
Відзначимо просте, але корисне спостереження.
\(A\)Дозволяти бути\(m\times n\) матрицею. Тоді\[A\vec{x} \cdot \vec{y} = \vec{x}\cdot A^T\vec{y}\nonumber \]
- Доказ
-
Це випливає з визначень:\[A\vec{x} \cdot \vec{y}=\sum_{i,j}a_{ij}x_{j} y_{i} =\sum_{i,j}x_{j} a_{ji} y_{i}= \vec{x} \cdot A^T\vec{y}\nonumber \]
Наступний наслідок дає техніка найменших квадратів.
Конкретне значення\(\vec{x}\), яке вирішує задачу Теореми,\(\PageIndex{5}\) виходить при розв'язанні рівняння.\[A^TA\vec{x}=A^T\vec{y}\nonumber \] Крім того, завжди існує розв'язок цієї системи рівнянь.
- Доказ
-
Для\(\vec{x}\) мінімізатора теореми\(\PageIndex{5}\),\(\left( \vec{y}-A\vec{x}\right) \cdot A \vec{u} =0\) для всіх\(\vec{u} \in \mathbb{R}^{n}\) і від Лемми\(\PageIndex{1}\), це те саме, що говорити\[A^T\left( \vec{y}-A\vec{x}\right) \cdot \vec{u}=0\nonumber \] для всіх\(u \in \mathbb{R}^{n}.\) Це означає\[A^T\vec{y}-A^TA\vec{x}=\vec{0}.\nonumber \] Тому існує рішення рівняння цього наслідку, і воно вирішує задача мінімізації теореми\(\PageIndex{5}\).
Зауважте, що\(\vec{x}\) може бути не унікальним\(A\vec{x}\), але найближча точка\(A\left(\mathbb{R}^{n}\right)\) до\(\vec{y}\) є унікальною, як було показано у наведеному вище аргументі.
Розглянемо наступний приклад.
Знайдіть рішення для системи найменших квадратів\[\left[ \begin{array}{rr} 2 & 1 \\ -1 & 3 \\ 4 & 5 \end{array} \right] \left[ \begin{array}{c} x \\ y \end{array} \right] =\left[ \begin{array}{c} 2 \\ 1 \\ 1 \end{array} \right]\nonumber \]
Рішення
Спочатку розглянемо, чи існує реальне рішення. Для цього встановіть розширену матрицю, задану Зведеною\[\left[ \begin{array}{rr|r} 2 & 1 & 2 \\ -1 & 3 & 1 \\ 4 & 5 & 1 \end{array} \right]\nonumber \] рядково-ешелоновою формою цієї доповненої матриці\[\left[ \begin{array}{rr|r} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right]\nonumber \]
Звідси випливає, що реального рішення цієї системи немає. Тому ми хочемо знайти рішення найменших квадратів. Нормальні рівняння є,\[\begin{aligned} A^T A \vec{x} &= A^T \vec{y} \\ \left[ \begin{array}{rrr} 2 & -1 & 4 \\ 1 & 3 & 5 \end{array} \right] \left[ \begin{array}{rr} 2 & 1 \\ -1 & 3 \\ 4 & 5 \end{array} \right] \left[ \begin{array}{c} x \\ y \end{array} \right] &=\left[ \begin{array}{rrr} 2 & -1 & 4 \\ 1 & 3 & 5 \end{array} \right] \left[ \begin{array}{c} 2 \\ 1 \\ 1 \end{array} \right]\end{aligned}\] і тому нам потрібно вирішити систему\[\left[ \begin{array}{rr} 21 & 19 \\ 19 & 35 \end{array} \right] \left[ \begin{array}{c} x \\ y \end{array} \right] =\left[ \begin{array}{r} 7 \\ 10 \end{array} \right]\nonumber \] Це звична вправа і рішення\[\left[ \begin{array}{c} x \\ y \end{array} \right] =\left[ \begin{array}{c} \frac{5}{34} \\ \frac{7}{34} \end{array} \right]\nonumber \]
Розглянемо ще один приклад.
Знайдіть рішення для системи найменших квадратів\[\left[ \begin{array}{rr} 2 & 1 \\ -1 & 3 \\ 4 & 5 \end{array} \right] \left[ \begin{array}{c} x \\ y \end{array} \right] =\left[ \begin{array}{c} 3 \\ 2 \\ 9 \end{array} \right]\nonumber \]
Рішення
Спочатку розглянемо, чи існує реальне рішення. Для цього встановіть розширену матрицю, задану Зведеною\[\left[ \begin{array}{rr|r} 2 & 1 & 3 \\ -1 & 3 & 2 \\ 4 & 5 & 9 \end{array} \right]\nonumber\] рядково-ешелоновою формою цієї доповненої матриці\[\left[ \begin{array}{rr|r} 1 & 0 & 1 \\ 0 & 1 & 1 \\ 0 & 0 & 0 \end{array} \right]\nonumber \]
Звідси випливає, що система має рішення, дане\(x=y=1\). Однак ми також можемо використовувати нормальні рівняння і знайти рішення найменших квадратів. \[\left[ \begin{array}{rrr} 2 & -1 & 4 \\ 1 & 3 & 5 \end{array} \right] \left[ \begin{array}{rr} 2 & 1 \\ -1 & 3 \\ 4 & 5 \end{array} \right] \left[ \begin{array}{c} x \\ y \end{array} \right] =\left[ \begin{array}{rrr} 2 & -1 & 4 \\ 1 & 3 & 5 \end{array} \right] \left[ \begin{array}{r} 3 \\ 2 \\ 9 \end{array} \right]\nonumber \]Тоді\[\left[ \begin{array}{rr} 21 & 19 \\ 19 & 35 \end{array} \right] \left[ \begin{array}{c} x \\ y \end{array} \right] =\left[ \begin{array}{c} 40 \\ 54 \end{array} \right]\nonumber \]
Рішення найменших квадратів - це те саме,\[\left[ \begin{array}{c} x \\ y \end{array} \right] =\left[ \begin{array}{c} 1 \\ 1 \end{array} \right]\nonumber \] що і рішення, знайдене вище.
Важливим застосуванням слідства\(\PageIndex{1}\) є проблема знаходження лінії регресії найменших квадратів у статистиці. Припустимо, вам задані точки на\(xy\) площині,\[\left\{ \left( x_{1},y_{1}\right), \left( x_{2},y_{2}\right), \cdots, \left( x_{n},y_{n}\right) \right\}\nonumber \] і ви хотіли б знайти константи\(m\) і\(b\) такі, що лінія\(\vec{y}=m\vec{x}+b\) проходить через всі ці точки. Звичайно, це буде неможливо взагалі. Тому намагаємося знайти\(m,b\) таку, щоб лінія була максимально близькою. Бажана система
\[\left[ \begin{array}{c} y_{1} \\ \vdots \\ y_{n} \end{array} \right] =\left[ \begin{array}{cc} x_{1} & 1 \\ \vdots & \vdots \\ x_{n} & 1 \end{array} \right] \left[ \begin{array}{c} m \\ b \end{array} \right]\nonumber \]
який має форму\(\vec{y}=A\vec{x}\). Бажано вибрати\(m\) і\(b\) зробити
\[\left \| A\left[ \begin{array}{c} m \\ b \end{array} \right] -\left[ \begin{array}{c} y_{1} \\ \vdots \\ y_{n} \end{array} \right] \right \| ^{2}\nonumber \]
якомога менше. Згідно з теоремою\(\PageIndex{5}\) та наслідками\(\PageIndex{1}\), найкращі значення для\(m\) та\(b\) зустрічаються як рішення
\[A^{T}A\left[ \begin{array}{c} m \\ b \end{array} \right] =A^{T}\left[ \begin{array}{c} y_{1} \\ \vdots \\ y_{n} \end{array} \right] ,\ \;\mbox{where}\; A=\left[ \begin{array}{cc} x_{1} & 1 \\ \vdots & \vdots \\ x_{n} & 1 \end{array} \right]\nonumber \]
Таким чином, обчислювальні\(A^{T}A,\)
\[\left[ \begin{array}{cc} \sum_{i=1}^{n}x_{i}^{2} & \sum_{i=1}^{n}x_{i} \\ \sum_{i=1}^{n}x_{i} & n \end{array} \right] \left[ \begin{array}{c} m \\ b \end{array} \right] =\left[ \begin{array}{c} \sum_{i=1}^{n}x_{i}y_{i} \\ \sum_{i=1}^{n}y_{i} \end{array} \right]\nonumber \]
Розв'язування цієї системи рівнянь для\(m\) і\(b\) (на прикладі правила Крамера) дає:
\[m= \frac{-\left( \sum_{i=1}^{n}x_{i}\right) \left( \sum_{i=1}^{n}y_{i}\right) +\left( \sum_{i=1}^{n}x_{i}y_{i}\right) n}{\left( \sum_{i=1}^{n}x_{i}^{2}\right) n-\left( \sum_{i=1}^{n}x_{i}\right) ^{2}}\nonumber \]і\[b=\frac{-\left( \sum_{i=1}^{n}x_{i}\right) \sum_{i=1}^{n}x_{i}y_{i}+\left( \sum_{i=1}^{n}y_{i}\right) \sum_{i=1}^{n}x_{i}^{2}}{\left( \sum_{i=1}^{n}x_{i}^{2}\right) n-\left( \sum_{i=1}^{n}x_{i}\right) ^{2}}.\nonumber \]
Розглянемо наступний приклад.
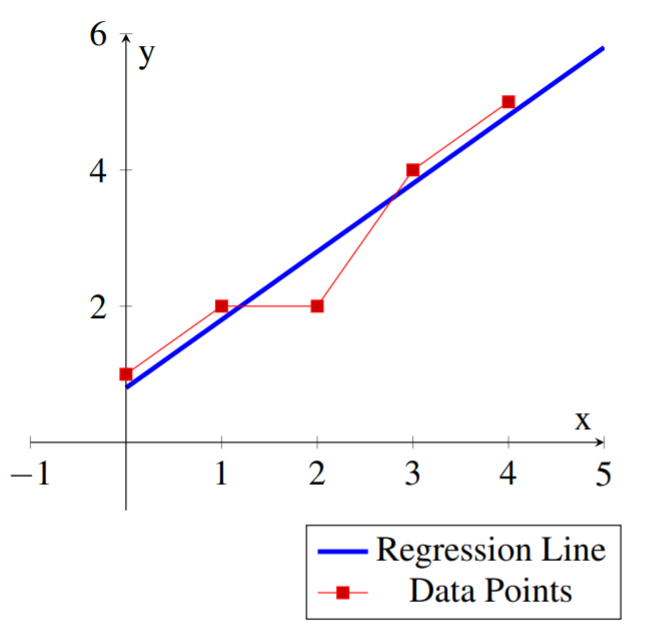
Знайдіть лінію регресії найменших квадратів\(\vec{y}=m\vec{x}+b\) для наступного набору точок даних:\[\left\{ (0,1), (1,2), (2,2), (3,4), (4,5) \right\} \nonumber\]
Рішення
У цьому випадку у нас є точки\(n=5\) даних, і ми отримуємо:\[\begin{array}{ll} \sum_{i=1}^{5}x_{i} = 10 & \sum_{i=1}^{5}y_{i} = 14 \\ \\ \sum_{i=1}^{5}x_{i}y_{i} = 38 & \sum_{i=1}^{5}x_{i}^{2} = 30\\ \end{array}\nonumber \] а отже\[\begin{aligned} m &= \frac{- 10 * 14 + 5*38}{5*30-10^2} = 1.00 \\ \\ b &= \frac{- 10 * 38 + 14*30}{5*30-10^2} = 0.80 \\\end{aligned}\]
Лінія регресії найменших квадратів для множини точок даних:\[\vec{y} = \vec{x}+.8\nonumber \]
Цей рядок можна використовувати для наближення інших значень даних. Наприклад, для\(x=6\) одного можна було б використовувати\(y(6)=6+.8=6.8\) як приблизне значення для даних.
Наступна діаграма показує точки даних і відповідну лінію регресії.
Таким же чином можна було б чітко зробити найменші квадрати,\(y=ax^{2}+bx+c\) придатні для кривих форми. У цьому випадку ви хочете вирішити якомога краще для\(a,b,\) і системи,\[\left[ \begin{array}{ccc} x_{1}^{2} & x_{1} & 1 \\ \vdots & \vdots & \vdots \\ x_{n}^{2} & x_{n} & 1 \end{array} \right] \left[ \begin{array}{c} a \\ b \\ c \end{array} \right] =\left[ \begin{array}{c} y_{1} \\ \vdots \\ y_{n} \end{array} \right]\nonumber \] і\(c\) один буде використовувати ту ж техніку, що і вище. Багато інших подібних проблем важливі, в тому числі багато в більш високих вимірах, і всі вони вирішуються однаково.
