15.3: Групи перестановок

Last updated
Save as PDF

Page ID: 65082

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Симетричні групи

Ризикуючи приголомшити розум читача, ми зараз розглянемо групи, елементами яких є функції. Нагадаємо, що перестановка на множині$A$ - це біекція з$A$ в$A\text{.}$ Припустимо, що$A = \{1, 2, 3\}\text{.}$ Існують$3! = 6$ різні перестановки$A\text{.}$ Ми будемо називати набір всіх 6 перестановок$S_3\text{.}$ Вони перераховані в наступній таблиці. Матрична форма опису функції на скінченній множині полягає в тому, щоб перерахувати домен у верхньому рядку та зображення кожного елемента безпосередньо під ним. Наприклад$r_1(1) = 2\text{.}$

Таблиця $\PageIndex{1}$: Елементи$S_{3}$

$i =\left( \begin{array}{ccc} 1 & 2 & 3 \\ 1 & 2 & 3 \\ \end{array} \right)$	$r_1=\left( \begin{array}{ccc} 1 & 2 & 3 \\ 2 & 3 & 1 \\ \end{array} \right)$	$r_2=\left( \begin{array}{ccc} 1 & 2 & 3 \\ 3 & 1 & 2 \\ \end{array} \right)$
$f_1=\left( \begin{array}{ccc} 1 & 2 & 3 \\ 1 & 3 & 2 \\ \end{array} \right) $	$f_2=\left( \begin{array}{ccc} 1 & 2 & 3 \\ 3 & 2 & 1 \\ \end{array} \right)$	$f_3=\left( \begin{array}{ccc} 1 & 2 & 3 \\ 2 & 1 & 3 \\ \end{array} \right)$

Операція, яка дасть структуру групи$\left\{i,r_1,r_2,f_1,f_2,f_3\right\}$, - це функціональна композиція. Розглянемо «продукт»$r_1\circ f_3\text{:}$

\ begin {рівняння*}\ почати {масив} {c} r_1\ circ f_3 (1) =r_1\ ліворуч (f_3 (1)\ праворуч) = r_1 (2) =3\ r_1\ circ f_3 (2) =r_1\ ліворуч (f_3 (2)\ праворуч) = r_1 (1) = 2\ r_1 (2) _1\ коло f_3 (3) =r_1\ ліворуч (f_3 (3)\ праворуч) = r_1 (3) = 1\\ end {масив}\ текст {.} \ end {рівняння*}

Зображення 1, 2 і 3 під$r_1\circ f_3$ і$f_2$ ідентичні. Таким чином, за визначенням рівності для функцій можна сказати$r_1\circ f_3=f_2$. Повна таблиця для роботи композиції функцій наведена в табл$\PageIndex{2}$.

Таблиця$\PageIndex{2}$: Операційний стіл для$S_{3}$

$\begin{array}{c|cccccc} \circ & i &r_1 & r_2 & f_1 & f_2 & f_3 \\ \hline i & i &r_1 & r_2 & f_1 & f_2 & f_3 \\ r_1 & r_1 &r_2 & i & f_3 & f_1 & f_2 \\ r_2 & r_2 &i & r_1 & f_2 & f_3 & f_1 \\ f_1 & f_1 & f_2 & f_3 & i & r_1 & r_2 \\ f_2 & f_2 &f_3 & f_1 & r_2 & i & r_1 \\ f_3 & f_3 & f_1 & f_2 & r_1 & r_2 & i \\ \end{array}$

Список$\PageIndex{1}$

Нам навіть не потрібна таблиця, щоб перевірити, чи є у нас група. Виходячи з наступних спостережень, множина всіх перестановок на будь-якому скінченному множині буде групою.

Функціональний склад завжди асоціативний.
Ідентифікатором для групи є$i\text{.}$ Якщо$g$ є будь-яка з перестановок$A$ і$x\in A\text{,}$
\ begin {рівняння*}\ begin {масив} {lr} (g\ circ i) (x) = g (i (x)) = g (x) & (i\ circ g) (x) = i (g (x)) = g (x)\\ end {масив}\ end {рівняння*
}$g\circ i = i\circ g=g\text{.}$
Перестановка, за визначенням, є біекцією. У главі 7 ми довели, що це означає, що він повинен мати зворотне, а сам зворотний є біекцією і, отже, перестановкою. Отже, всі елементи$S_3$ мають зворотну в$S_3\text{.}$ Якщо перестановка відображається у вигляді матриці, її зворотну можна отримати шляхом обміну двома рядками та перестановкою стовпців так, щоб верхній рядок був у порядку. Першого кроку насправді достатньо для отримання зворотного, але сортування верхнього ряду полегшує розпізнавання зворотного.
Для прикладу розглянемо типову перестановку на$\{1,2,3,4,5\}\text{,}$$f= \left( \begin{array}{ccccc} 1 & 2 & 3 & 4 & 5 \\ 5 & 3 & 2 & 1 & 4 \\ \end{array} \right)\text{.}$
\ begin {рівняння*} f^ {-1} =\ left (\ begin {масив} {ccccc} 5 & 3 & 2 & 4\\ 1 & 2 & 3 & 4 & 5\\ end {масив}\ праворуч) =\ left (\ begin {масив} {ccccc} 1 & 2 & 3 & 3 & 3 & 3 & підсилювач; 4 & 5\\ 4 & 3 & 2 & 5 & 1\\\ кінець {масив}\ праворуч)\ текст {.} \ end {рівняння*}

Примітка$\PageIndex{1}$

З таблиці ми бачимо$\PageIndex{2}$, що$S_3$ це не абелево. Пам'ятайте, неабелево - це заперечення абеля. Існування двох елементів, які не їздять на роботу, є достатнім, щоб зробити групу не-абелею. У цій$r_1$ групі і$f_3$ є одна така пара:$r_1\circ f_3= f_2$ хоча$f_3\circ r_1= f_1\text{,}$ так$r_1\circ f_3\neq f_3\circ r_1\text{.}$ Обережно: Не приймайте це, щоб означати, що кожна пара елементів повинна мати цю властивість. Є кілька пар елементів$S_3$, які роблять коммутіруют. Насправді, особистість,$i\text{,}$ повинна їздити з усім. Також кожен елемент повинен їздити на роботу зі своїм зворотним.

Визначення $\PageIndex{1}$: Symmetric Group

$A$Дозволяти бути непорожнім набором. Множина всіх перестановок на$A$ з операцією композиції функції називається симетричною групою на$A\text{,}$ позначеному$S_A\text{.}$

Кардинальність скінченної$A$ множини більш значуща, ніж елементи, і позначимо симетричною групою на будь-якому наборі кардинальності$S_n$$n\text{,}$$n\geq 1\text{.}$

Приклад$\PageIndex{1}$: The Significance of $S_3$

Наш$S_3\text{,}$ вступний приклад - найменша неабелівська група. З цієї причини всі його власні підгрупи є абелевими: насправді всі вони циклічні. $\PageIndex{1}$На малюнку показана діаграма Хассе для підгруп$S_3\text{.}$

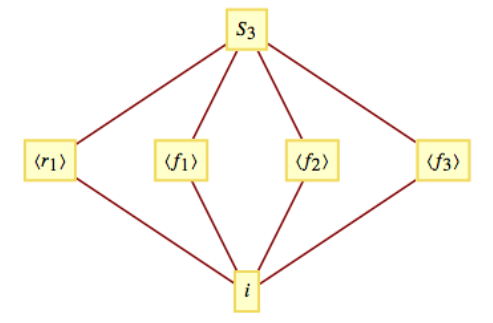$clipboard_e6af63a63397c1e187f3bf49d5a2cce05.png$ Малюнок$\PageIndex{1}$: Гратчаста діаграма підгруп$S_3$

Приклад$\PageIndex{2}$: Smallest Symmetric Groups

Єдині абелеві симетричні групи - це$S_1$ і$S_2$, з 1 і 2 елементами відповідно. Елементи$S_2$ є$i = \left( \begin{array}{cc} 1 & 2 \\ 1 & 2 \\ \end{array} \right)$ і$\alpha = \left( \begin{array}{cc} 1 & 2 \\ 2 & 1 \\ \end{array} \right)\text{.}$$S_2$ є ізоморфними до$\mathbb{Z}_2\text{.}$

Теорема$\PageIndex{1}$

Для$n \geq 1\text{,}$$\lvert S_n\rvert =n!$ і для не$n \geq 3\text{,}$$S_n$ є абелевим.

Доказ: Перша частина теореми випливає з розширеного правила продуктів (див. Главу 2). Деталі доказу другої частини залишаємо читачеві після наступної підказки. Розглянемо$f$,$S_n$ де$f(1) = 2\text{,}$$f(2) = 3\text{,}$$f(3) = 1\text{,}$ і$f(j) = j$ для$3 < j \leq n\text{.}$ Тому цикл подання$f$$(1,2,3)\text{.}$ тепер визначити аналогічним$g$ чином, так що при порівнянні$f(g(1))$ і$g(f(1))$ ви отримаєте різні результати.

Цикл позначення

Другий спосіб опису перестановки - за допомогою циклів, які ми познайомимо спочатку на прикладі. Розглянемо$f\in S_8$ визначення за допомогою знайомих тепер матричних позначень:

\ begin {рівняння*} f=\ ліворуч (\ begin {масив} {cccccccc} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8\\ 8 & 2 & 7 & 7 & 7 & 6 & 6 & 5 & 1 & 3\\\ кінець {масив}\ праворуч)\ кінець {рівняння*}

Розглянемо зображення 1, коли$f$ застосовується повторно. Зображення$f(1)\text{,}$$f(f(1))\text{,}$$f(f(f(1))), \ldots$ на$8, 3, 7, 1, 8, 3, 7,\ldots\text{.}$ малюнку$\PageIndex{2}$ (а) ця ситуація представлена графіком з вершинами 1, 8, 3 та 7 і показує, що значення, які ви отримуєте, багаторазово застосовуючи$f$ цикл через ці значення. Ось чому ми називаємо цю частину$f$ циклом довжиною 4. Звичайно, починаючи з 8, 3 або 7 також виробляє той же цикл із зміною лише початкового значення.

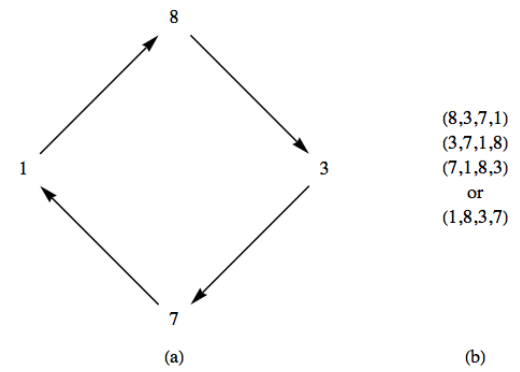$clipboard_ec0e238598d3084420f9956a0a90366a9.png$ Малюнок$\PageIndex{2}$: Уявлення циклу довжиною 4

Малюнок$\PageIndex{2}$ (а) ілюструє, як цикл може бути представлений наочно, але писати трохи незручно. Частина (б) малюнка представляє більш загальновизнаний спосіб написання циклу. У (b) цикл представлений списком, де зображення будь-якого числа у списку є його наступником. Крім того, останнє число в списку має в якості зображення перше число.

Інші елементи області ніколи не досягаються, якщо ви починаєте цикл,$(1,8,3,7)\text{,}$ і тому дивлячись на зображення цих інших чисел буде виробляти числа, які не з'єднані з$\{1,8,3,7\}\text{.}$ множиною Інші неспільні цикли$f$ є (2), (4, 6) і (5).$f$ Ми можемо висловити$f$ як добуток неспільних циклів:$f= (1, 8, 3, 7)(2)(4, 6)(5)$ або$f= (1,8,3,7)(4,6)\text{,}$ де відсутність 2 і 5 означає, що$f(2) = 2$ і$f(5) = 5\text{.}$

Примітка$\PageIndex{2}$: Disjoint Cycles

Ми говоримо, що два цикли неспільні, якщо в обох циклах не з'являється число, як це відбувається в наших виразах$f$ вище. Розчленовані цикли можуть бути записані в будь-якому порядку. Таким чином, ми могли б також сказати, що$f=(4,6)(1,8,3,7)\text{.}$

Примітка$\PageIndex{3}$: Composition of Permutations

Ми зараз розглянемо склад перестановок, написаних в циклічній формі на прикладі. Припустимо, що$f = (1,8, 3, 7)(4, 6)$ і$g = (1, 5, 6)(8, 3, 7, 4)$ є елементами$S_8\text{.}$ Для обчислення$f\circ g\text{,}$ ми починаємо з простої конкатенації:

\[\label{eq:1}f\circ g=(1,8,3,7)(4,6)(1,5,6)(8,3,7,4)\]

Хоча це дійсний вираз для$f \circ g\text{,}$ нашої мети є висловити композицію як продукт неспільних циклів, як$f$ і$g$ були написані окремо. Почнемо з визначення циклу, який містить 1. При об'єднанні будь-якої кількості циклів вони завжди читаються справа наліво, як і при всіх функціях. Перший цикл в$\eqref{eq:1}$ не містить 1; таким чином ми переходимо до другого. Зображення 1 за цим циклом дорівнює 5. Тепер переходимо до наступного циклу, шукаємо 5, які не з'являються. Четвертий цикл також не містить 5; так$f\circ g(1) = 5\text{.}$

На цьому етапі ми б написали «$f \circ g = (1,5 $» на папері. Повторюємо кроки для визначення$f\circ g(5)\text{.}$ Цього разу другий цикл$\eqref{eq:1}$ ходів 5 до 6, а потім третій цикл рухається 6 до 4. Тому,$f\circ g(5) = 4\text{.}$ Ми продовжуємо до завершення циклу (1, 5, 4, 3), визначаючи, що$f\circ g(3) = 1\text{.}$ Процес потім повторюється, починаючи з будь-якого числа, яке не відображається в циклі (ах), які вже завершені.

Кінцевий результат для нашого прикладу -$f \circ g = (1, 5, 4, 3)(6, 8, 7)\text{.}$$f(2) = 2$$g(2) = 2\text{,}$$f\circ g(2) = 2$ Since і і нам не потрібно включати один цикл (2) в кінцевий результат, хоча він може бути включений.

Приклад$\PageIndex{3}$: Some Compositions

$\displaystyle (1, 2, 3, 4)(1, 2, 3, 4) = (1, 3)(2, 4)$
$(1, 4)(1, 3)(1, 2) = (1, 2, 3, 4)\text{.}$

Зверніть увагу, що циклічні позначення не вказують на набір, який переставляється. Наведені вище приклади можуть бути$S_5\text{,}$ там, де зображення 5 дорівнює 5. Ця неоднозначність, як правило, долається, роблячи контекст зрозумілим на початку дискусії.

Визначення$\PageIndex{2}$: Transposition

Транспозиція - це цикл довжини 2.

Спостереження$\PageIndex{1}$: About Transpositions

$f= (1, 4)$і$g=(4,5)$ є транспозиціями в$S_5\text{.}$ Однак,$f\circ g = (1,4, 5)$ і не$g \circ f = (1, 5, 4)$ є транспозиціями; Таким чином, набір транспозицій не закривається під композицією. Так як$f^2=f\circ f$ і$g^2=g\circ g$ рівні перестановці ідентичності,$f$ і$g$ є власними оберненнями. По суті, кожна транспозиція - це своя зворотна.

Теорема$\PageIndex{2}$: Decomposition into Cycles

Кожен цикл довжини більше 2 може бути виражений як добуток транспозицій.

Доказ

Потрібно лише вказати, яким чином можна отримати добуток транспозицій. Легко перевірити, що цикл довжини$k\text{,}$$\left(a_1, a_2, a_3, \ldots , a_k\right)\text{,}$ дорівнює наступному добутку$k-1$ транспозицій:

\ begin {рівняння*}\ лівий (a_1, a_k\ правий)\ cdots\ лівий (a_1, a_3\ правий)\ лівий (a_1, a_2\ правий)\ кінець {рівняння*}

Звичайно, продукт циклів може бути записаний як твір транспозицій так само легко, застосовуючи наведене вище правило до кожного циклу. Наприклад,

\ begin {рівняння*} (1, 3, 5, 7) (2, 4, 6) = (1, 7) (1, 5) (1, 5) (1, 3) (2, 6) (2, 4)\ end {рівняння*}

На відміну від ситуації з нероз'єдненими циклами, ми не вільні змінювати порядок цих транспозицій.

Парність перестановок і змінна група

Розкладання перестановок на транспозиції дає можливість класифікувати їх і виявити важливе сімейство груп.

Докази наступної теореми фігурують у багатьох текстах абстрактної алгебри.

Теорема$\PageIndex{3}$

Кожна перестановка на скінченній множині може бути виражена як добуток парної кількості транспозицій або непарної кількості транспозицій, але не обох.

Теорема$\PageIndex{3}$ говорить про те, що її$S_n$ можна розділити на «парні» і «непарні» елементи. Наприклад, парні перестановки$S_3$ є$i\text{,}$$r_1=(1,2,3)=(1,3)(1,2)$ і$r_2=(1,3,2)=(1,2)(1,3)\text{.}$ Вони утворюють підгрупу,$\left\{i,r_1,r_2\right\}$$S_3\text{.}$

Загалом:

Визначення $\PageIndex{3}$: The Alternating Group

Нехай$n \geq 2\text{.}$ Множина парних перестановок в$S_n$ є власною підгрупою$S_n$ називається змінною групою на$\{1, 2, \ldots, n\}\text{,}$ позначені$A_n\text{.}$

Ми обґрунтовуємо наше твердження, що$A_n$ це група:

Теорема$\PageIndex{4}$

Нехай$n \geq 2\text{.}$ Чергуюча група дійсно є групою і має порядок$\frac{n!}{2}\text{.}$

Доказ

У цьому$s_i$ доказі символи і$t_i$ позначають транспозиції і$p\text{,}$$q$ є навіть невід'ємними цілими числами. Якщо$f, g \in A_n\text{,}$ ми можемо записати дві перестановки як добуток парних чисел транспозицій,$f=s_1s_2\cdots s_p$ а$g=t_1t_2\cdots t_q\text{.}$ потім

\ begin {рівняння*} f\ коло g=s_1s_2\ cdots s_pt_1t_2\ cdots t_q\ end {рівняння*}

Так як$p+q$ рівний,$f\circ g \in A_n\text{,}$ і$A_n$ закритий по відношенню до функції складу. Цим ми довели, що$A_n$ це підгрупа$S_n$ по теоремі 11.5.2.

Щоб довести остаточне твердження, нехай$B_n$ буде набір непарних перестановок і нехай$\tau = (1,2)\text{.}$ Визначити$\theta: A_n \to B_n$$\theta(f) = f\circ \tau\text{.}$ припустимо, що$\theta(f) = \theta(g)\text{.}$ тоді$f\circ \tau = g\circ \tau $ і за правом скасування закону,$f = g\text{.}$ Отже,$\theta$ є ін'єкцією. Далі ми показуємо, що$\theta$ це також відрижка. Якщо$h \in B_n\text{,}$$h$ це зображення елемента$A_n\text{.}$ конкретно,$h$ це зображення$h\circ \tau\text{.}$

\ begin {рівняння*}\ почати {спліт}\ тета (h\ circ\ tau) & = (h\ circ\ tau)\ circ\ tau\ & = h\ circ (\ tau\ circ\ tau)\ quad\ textrm {Чому?} \\ & = h\ circ i\ quad\ textrm {Чому?} \\ & = h\\\ кінець {спліт}\ кінець {рівняння*}

Так як$\theta$ є біекція,$\lvert A_n \rvert =\lvert B_n\rvert =\frac{n!}{2}\text{.}$

Приклад$\PageIndex{4}$: The Sliding Tile Puzzle

Розглянемо розсувні плитки пазли, зображені на малюнку$\PageIndex{3}$. Кожен пронумерований квадрат - це плитка, а темний квадрат - розрив. Будь-яка плитка, яка прилягає до зазору, може ковзати в зазор. У більшості версій цієї головоломки плитки замкнені в рамку, щоб їх можна було переміщати тільки описаним вище способом. Мета головоломки полягає в тому, щоб розташувати плитки так, як вони відображаються в Configuration (a). Конфігурації (b) і (c) є типовими відправними точками. Пропонуємо показати, чому головоломку можна вирішити, починаючи з (b), але не з (c).

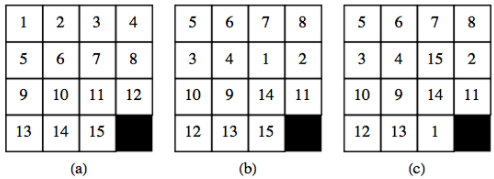$clipboard_e0fe47a67b122c6061c88edcd2affc1f3.png$ Малюнок$\PageIndex{3}$: Конфігурації розсувної плитки головоломки

Ми пов'яжемо зміну конфігурації головоломки з елементом$S_{16}\text{.}$ Imagine, що плитка під номером 16 заповнює прогалину. Для будь-якої конфігурації головоломки ідентичність$i\text{,}$ - це функція, яка залишає конфігурацію «як є». Загалом, якщо$f \in S_{16}\text{,}$ і$1 \leq k \leq 16\text{,}$$f(k)$ є позицією, до якої$k$ пересувається плитка в положенні$f$, що з'являється в положенні конфігурації (a).$k$ Якщо викликати функції, які, починаючи з configuration (a), призводять до конфігурації (b) і (c) за іменами$f_1$ і$f_2\text{,}$ відповідно,

\ почати {рівняння*} f_1 = (1, 5, 3, 7) (2, 6, 4, 8) (9, 10) (11, 14, 13, 12) (15) (16)\ кінець {рівняння*}

\ почати {рівняння*} f_2 = (1, 5, 3, 7, 15) (2, 6, 4, 8) (9, 10) (11, 14, 13, 12) (16). \ end {рівняння*}

Як ми можемо інтерпретувати рух однієї плитки як перестановку? Розглянемо, що відбувається, коли 12 плиток$i$ ковзає в щілину. Результатом є конфігурація, яку ми б інтерпретували$(12,16)\text{,}$ як одну транспозицію. Тепер, якщо ми посунемо плитку 8 в положення 12, результат або$(8, 16, 12)\text{.}$ Отже, «обміняючи» плитки 8 і 16, ми реалізували функцію$(8, 12) (12, 16) = (8, 12, 16)\text{.}$

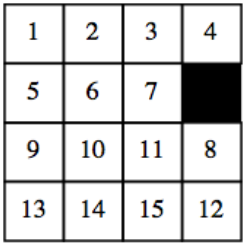$clipboard_ef4878acb2a6c0421ec4966032cf9ec64.png$ Малюнок$\PageIndex{4}$: Конфігурація$(8,12,16)$

Кожен раз, коли ви ковзаєте плитку в щілину, нова перестановка - це транспозиція, складена зі старою перестановкою. Тепер зауважте, що щоб почати з початкової конфігурації і закінчитися після кінцевої кількості ходів з розривом у вихідному положенні, необхідно зробити парну кількість ходів. Таким чином, конфігурація, що відповідає будь-якій перестановці, яка залишає 16 фіксованими, не може бути вирішена, якщо перестановка непарна. Зверніть увагу, що$f_2$ це непарна перестановка; таким чином, Puzzle (c) не може бути вирішена. Доказ того, що всі навіть перестановки, такі як$f_1\text{,}$ можуть бути вирішені, залишається зацікавленому читачеві переслідувати.

Двогранні групи

Спостереження$\PageIndex{2}$: Realization of Groups

На даний момент ми бачили кілька випадків, коли група може з'явитися через ізоморфну копію себе в різних налаштуваннях. Найпростіший такий приклад - циклічна група порядку 2. Коли ця група згадується, ми могли б, природно, думати про групу,$\left[\mathbb{Z}_2;+_2\right]\text{,}$ але групи$[\{-1,1\};\cdot ]$ і$\left[S_2;\circ \right]$ ізоморфні для неї. Жодна з цих груп не обов'язково є більш природною або важливою, ніж інші. Який з них ви використовуєте, залежить від ситуації, в якій ви перебуваєте, і всі вони називаються реалізаціями циклічної групи порядку 2. Наступне сімейство груп, які ми будемо вивчати, двогранні групи, має дві природні реалізації, спочатку як перестановки, а друга як геометричні симетрії.

Сімейство двогранних груп індексується натуральними числами, більшими або рівними 3. Бо$k \geq 3\text{,}$$\mathcal{D}_k$ будуть мати$2k$ елементи. Спочатку опишемо елементи і операцію над ними за допомогою геометрії.

Ми можемо описати$\mathcal{D}_n$ через симетрії правильного$n$ -кутника ($n = 3\text{:}$рівносторонній трикутник,$n = 4\text{:}$ квадрат,$n = 5\text{:}$ правильний п'ятикутник,$\ldots $). Тут ми зосередимося лише на випадку$\mathcal{D}_4\text{.}$ Якщо квадрат закріплений у просторі, є кілька рухів квадрата, які в кінці руху не змінюватимуть видимого положення квадрата. Фактичні зміни положення можна побачити, якщо позначені кути квадрата. На$\PageIndex{5}$ малюнку показана початкова схема маркування разом з чотирма осями симетрії квадрата.

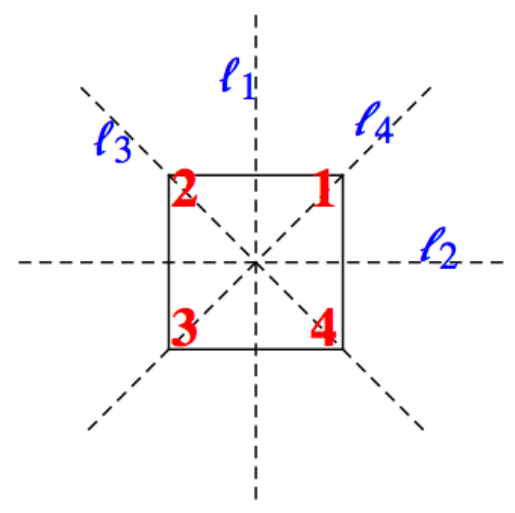$clipboard_e7f29c1a6bf681eda240dea44a5b5613b.png$ Малюнок$\PageIndex{5}$: Осі симетрії квадрата

Можливо, варто зробити такий квадрат за допомогою аркуша паперу. Будьте обережні, щоб позначити задню частину так, щоб цифри збігалися спереду. Два рухи квадрата будуть вважатися еквівалентними, якщо квадрат знаходиться в одному положенні після виконання будь-якого руху. Існує вісім різних рухів. Перші чотири є$0{}^{\circ}\text{,}$$90{}^{\circ}\text{,}$$180{}^{\circ}\text{,}$ і$270{}^{\circ}$ за годинниковою стрілкою обертання квадрата, а інші чотири є$180{}^{\circ}$ сальто вздовж осей$l_1\text{,}$$l_2\text{,}$$l_3\text{,}$ і$l_4\text{.}$ Ми будемо називати обертання$i, r_1\text{,}$$r_2\text{,}$ і$r_3\text{,}$ відповідно, і сальто$f_1\text{,}$$f_2\text{,}$$f_3\text{,}$ і$f_4\text{,}$ відповідно. Малюнок$\PageIndex{6}$ ілюструє$r_1$ і$f_1\text{.}$ Для подальшого посилання ми також включаємо перестановки, яким вони відповідають.

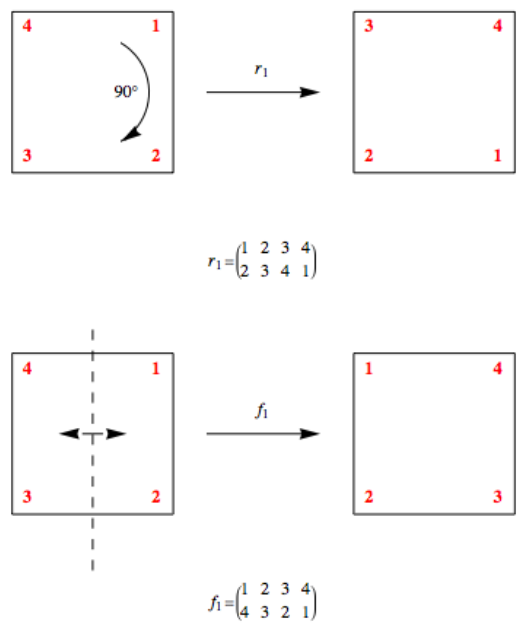$clipboard_e621f265899fef9b8660a1a925ce59d6a.png$ Малюнок$\PageIndex{6}$: Два елементи$\mathcal{D}_4$

Яка операція на цьому наборі симетрій? Ми назвемо операцію «з подальшим» і використаємо символ$*$ для її представлення. Операція буде полягати в поєднанні рухів, застосовуючи рухи справа наліво, як і з функціями. Ми проілюструємо, як$*$ обчислюється, знаходячи$r_1*f_1\text{.}$ Починаючи з початкової конфігурації, якщо виконати$f_1$ рух, а потім відразу ж виконати$r_1$ на результат, то отримаємо таку ж конфігурацію, як ніби ми тільки$f_4\text{,}$ що виконали, яка полягає в перевертанні квадрата уздовж лінії $l_4\text{.}$Тому$r_1*f_1 = f_4\text{.}$ важливим спостереженням є те, що$f_1*r_1 \neq f_4\text{,}$ означає, що ця група є неабелевою. Читачеві рекомендується переконатися в цьому самостійно.

Ми також можемо реалізувати двогранні групи як перестановки. Для будь-якого симетричного руху квадрата ми можемо пов'язати з ним перестановку. У випадку з$\mathcal{D}_4\text{,}$ зображеннями кожного з чисел від 1 до 4 - це позиції на квадраті, в які переміщений кожен з кутів 1 - 4. Наприклад, оскільки кут 4 переміщається в позицію 1 при виконанні$r_1\text{,}$ відповідної функції буде відображатися 4 на 1. Крім того, 1 отримує відображення 2, 2 до 3 і 3 до 4. Отже,$r_1$ відбувається цикл$(1,2,3,4)$. Фліп$f_1$ переносить дві пари кутів і відповідає$(1,4)(2,3)\text{.}$ Якщо ми хочемо об'єднати ці дві перестановки, використовуючи ті ж імена, що і при рухах, ми отримуємо

\ почати {рівняння*} r_1\ коло f_1= (1,2,3,4)\ коло (1,4) (2,3) = (1) (2,4) (3) = (2,4) = (2,4)\ кінець {рівняння*}

Зверніть увагу, що ця перестановка відповідає фліпу$f_4\text{.}$

Хоча$\mathcal{D}_4$ це не циклічний (оскільки він не є абелевим), він може бути згенерований з двох елементів$r_1$ і$f_1\text{:}$

\ begin {рівняння*}\ mathcal {D} _4=\ лівий\ кут r_1, f_1\ праворуч\ діапазон =\ вліво\ {i, r_1, r_1 {} ^2, r_1 {} ^3, f_1, r_1\ circ f_1, r_1 {} ^2\ circ f_1, r_1 {^3\ circ f_1\ право\}\ кінець {рівняння*}

Подібним чином описати будь-яку з двогранних груп досить просто. Ось формальне визначення

Визначення $\PageIndex{4}$: Dihedral Group

$n$Дозволяти натуральне число більше або дорівнює 3. Якщо$r= (1,2, \ldots , n)\text{,}$$n$ -цикл, а$f= (1,n)(2,n-1)\ldots$ потім

\ begin {рівняння*}\ mathcal {D} _n=\ лангол r, f\ діапазон =\ лівий\ {i, r, r^2,\ ldots, r^ {n-1}, f, r\ circ f, r^2\ circ f,\ ldots, r^ {n-1}\ circ f\ праворуч\}\ кінець {рівняння*}

- це двогранна група.$n$

Примітка$\PageIndex{4}$: Caution

Ви можете помітити, що ми використовуємо скрипт$D\text{,}$$\mathcal{D}\text{,}$ для двогранних груп. Іноді ви можете побачити звичайне$D$ в інших джерелах для двогранних груп. Не плутайте його з набором дільників,$n\text{,}$ які ми позначаємо$D_n\text{.}$ Зазвичай контекст обговорення повинен зробити сенс$D_n$ зрозумілим.

Приклад$\PageIndex{5}$: A Letter-Facing Machine

Застосування$\mathcal{D}_4$ є в конструкції машини, зверненої до листа. Уявіть собі букви, що входять до конвеєрної стрічки, щоб бути поштовий Вони розміщуються на стрічці конвеєра навмання так, щоб дві сторони були паралельні стрічці. Припустимо, що поштовий маркер може розпізнати штамп у верхньому правому куті конверта, збоку вгору. На малюнку показана послідовність машин$\PageIndex{7}$, які будуть розпізнавати штамп на будь-якій букві, незалежно від того, в якому положенні буква починається. Лист$P$ розшифровується як поштовий маркер. Букви$R$ і$F$ підставка для обертових і перевертають машин, які виконують рухи$r_1$ і$f_1\text{.}$

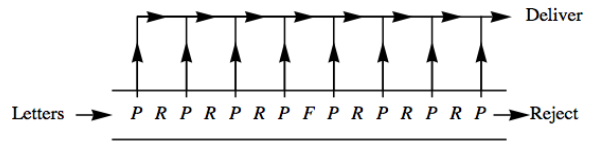$clipboard_ef5165616a5431e5a8c1709f8c96a107a.png$ Малюнок$\PageIndex{7}$: Літерна грань

Стрілки, спрямовані вгору, вказують на те, що якщо лист поштовий штемпель, він знімається з конвеєрної стрічки для доставки. Якщо лист доходить до кінця, на ньому не повинно бути штампа. Такі машини, що звертаються до листів, були розроблені (див. [16]). Одним з економічних міркувань є те, що$R$ -машини, як правило, коштують дорожче, ніж$F$ -машини. $R$-машини також, як правило, пошкоджують більше букв. Беручи до уваги ці факти, читачеві пропонується розробити кращу машину з листом. Припустимо, що$R$ -машини$\$800$ коштують і$F$ -машини$\$500\text{.}$ коштують Переконайтеся, що всі кути вхідних листів будуть розглянуті, коли вони йдуть вниз по конвеєрній стрічці.

Вправи

Вправа$\PageIndex{1}$

Задано$f=\left( \begin{array}{cccc} 1 & 2 & 3 & 4 \\ 2 & 1 & 4 & 3 \\ \end{array} \right)\text{,}$$g=\left( \begin{array}{cccc} 1 & 2 & 3 & 4 \\ 2 & 3 & 4 & 1 \\ \end{array} \right)\text{,}$ і$h=\left( \begin{array}{cccc} 1 & 2 & 3 & 4 \\ 3 & 2 & 4 & 1 \\ \end{array} \right)\text{,}$ обчислити

$\displaystyle f\circ g$
$\displaystyle g\circ h$
$\displaystyle (f\circ g)\circ h$
$\displaystyle f\circ (g\circ h)$
$\displaystyle h^{-1}$
$\displaystyle h^{-1} \circ g\circ h$
$\displaystyle f^{-1}$

Відповідь

$\displaystyle \left( \begin{array}{cccc} 1 & 2 & 3 & 4 \\ 1 & 4 & 3 & 2 \\ \end{array} \right)$
$\displaystyle \left( \begin{array}{cccc} 1 & 2 & 3 & 4 \\ 4 & 3 & 1 & 2 \\ \end{array} \right)$
$\displaystyle \left( \begin{array}{cccc} 1 & 2 & 3 & 4 \\ 3 & 4 & 2 & 1 \\ \end{array} \right)$
$\displaystyle \left( \begin{array}{cccc} 1 & 2 & 3 & 4 \\ 3 & 4 & 2 & 1 \\ \end{array} \right)$
$\displaystyle \left( \begin{array}{cccc} 1 & 2 & 3 & 4 \\ 4 & 2 & 1 & 3 \\ \end{array} \right)$
$\displaystyle \left( \begin{array}{cccc} 1 & 2 & 3 & 4 \\ 3 & 1 & 4 & 2 \\ \end{array} \right)$
$\displaystyle \left( \begin{array}{cccc} 1 & 2 & 3 & 4 \\ 2 & 1 & 4 & 3 \\ \end{array} \right)$

Вправа$\PageIndex{2}$

Написати$f\text{,}$$g\text{,}$ і$h$ з вправи$\PageIndex{1}$ як продукти неспільних циклів і визначити, чи є кожен непарним або парним.

Вправа$\PageIndex{3}$

Чи ліві косети$A_3=\left\{i,r_1,r_2\right\}$ над$S_3$ утворюють групу під індукованою операцією на лівих косетах$A_3\text{?}$ Що з лівими косетами$\left\langle f_1\right\rangle\text{?}$

Відповідь: $S_3/A_3$це група порядку два. Операція над лівими$H=\left\langle f_1\right\rangle$ косетами недостатньо визначена, тому група не може бути сформована з лівих косет$H\text{.}$

Вправа$\PageIndex{4}$

У його реалізації як перестановок двогранна група$\mathcal{D}_3$ дорівнює Чи$S_3\text{.}$ можете ви дати геометричне пояснення чому? Чому не$\mathcal{D}_4$ дорівнює$S_4\text{?}$

Вправа $\PageIndex{5}$

Заповніть список елементів$\mathcal{D}_4$ і випишіть таблицю для групи в її реалізації у вигляді симетрії.
Перерахуйте підгрупи$\mathcal{D}_4$ у гратковій діаграмі. Чи всі вони циклічні? До яких більш простим групам відносяться підгрупи$\mathcal{D}_4$ ізоморфних?

Відповідь

$\mathcal{D}_4 = \left\{i, r, r^2, r^3, f_1, f_2, f_3, f_4\right\}$$i$Де функція ідентичності,$r=\left( \begin{array}{cccc} 1 & 2 & 3 & 4 \\ 2 & 3 & 4 & 1 \\ \end{array} \right)\text{,}$ і

\ begin {рівняння*}\ begin {масив} {cc} f_1 =\ left (\ begin {масив} {cccc} 1 & 2 & 3\\ 4 & 3 & 2 & 1\\ кінець {масив}\ праворуч) & f_2 =\ left (\ begin {масив} {cccc} 1 & 2\\ 2 & 4 & 3\\ кінець {масив}\ праворуч)\\ f_3 =\ ліворуч (\ begin {масив} {cccc} 1 & 2 & 3 & 4\\ 3 & 2 & 1 & 4\\ кінець {масив}\ праворуч) & f_4 =\ left (\ begin {масив} {cccc} 1 & 2 & 3\\ 1 & 4 & 3 & 2\\\ кінець {масив}\ праворуч)\\ кінець {масив}\ кінець {рівняння*}

Операційна таблиця для групи

\ begin {рівняння*}\ почати {масив} {c|c}\ circ &\ textrm {}\ почати {масив} {cccccccc} i & r & r^2 & r^3 & f_2 & f_3 & f_4\\\ end {масив}\\ hline\ begin {масив} {c} i\\ r\ r^2\\ r^3\\ f_1\\ f_2\\ f_3\\ f_4\\ кінець {масив} &\ begin {масив} {ccccccccc} i & r & r^2 & ; r^3 & f_1 & f_2 & f_3 & f_4\\ r & r^2 & r^3 & я & f_4 & f_3 & f_1 & f_2\\ r^2 & r^3 & r & f_2 & f_2 & f_1 & f_4 & f_3\ r^3 & r ^ 2 & f_2 3 & f_4 & f_2 & f_1\\ f_1 & f_3 & f_2 & f_4 & i ; r^2 & r ^ 3\\ f_2 & f_4 & f_1 & f_3 & r^2 & я & r^3 & r\\ f_3 & f_2 & f_4 & f_1 & r^3 & r ^ 2\\ f_4 & f_3 & r^2\ f_4 & f_3 & f_2 & r ^3 & r^2 2 & i\\\ end {масив}\\ end {масив}\ кінець {рівняння*}

Гратчаста діаграма її підгруп

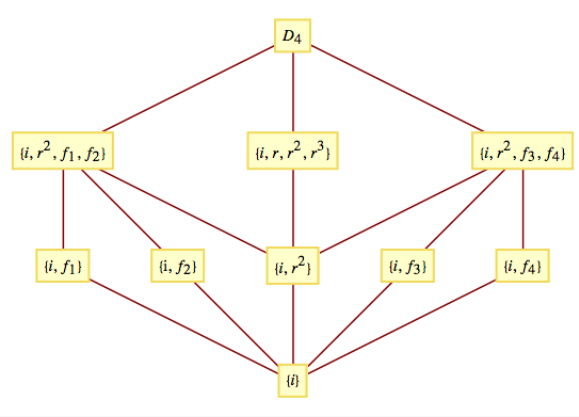$clipboard_e1b298e40762e846d0a25ba928ca9043e.png$ Малюнок$\PageIndex{8}$: Підгрупи$\mathcal{D}_4$

Всі власні підгрупи є циклічними, крім$\left\{i,r^2,f_1,f_2\right\}$$\textrm{ }\textrm{ }$ і$\left\{i,r^2,f_3,f_4\right\}\text{.}$ Кожна 2-елементна підгрупа ізоморфна до$\mathbb{Z}_2$;$\left\{i,r,r^2,r^3\right\}$ ізоморфна до$\mathbb{Z}_4$;$\left\{i,r^2,f_1,f_2\right\}$$\textrm{ }\textrm{ }$ і$\left\{i,r^2,f_3,f_4\right\}$ ізоморфна до$\mathbb{Z}_2\times \mathbb{Z}_2\text{.}$

Вправа$\PageIndex{6}$

Створіть кращу машину, звернену до букв (див. Приклад$\PageIndex{5}$). Як ви можете переконатися, що машина, звернена до листа, дійсно перевіряє кожен кут листа? Чи можна це зробити на папері, фактично не надсилаючи через неї листи?

Вправа$\PageIndex{7}$

Доведіть шляхом індукції, що якщо$r \geq 1$ і кожен$t_i\text{,}$ є транспозицією, то$\left(t_1\circ t_2\circ \cdots \circ t_r\right){}^{-1}=t_r\circ \cdots \circ t_2\circ t_1$

Відповідь: Одне з рішень - навести вправу 11.3.3 в кінці розділу 11.3. Він може бути безпосередньо застосований до цієї проблеми. Індукційний доказ проблеми під рукою був би майже ідентичним доказом більш загального твердження. $\left(t_1t_2\cdots t_r\right){}^{-1}= t_r{}^{-1}\cdots t_2{}^{-1}t_1{}^{-1}\quad\textrm{ by Exercise 11.3.3 of Section 11.3}\\ \\ \quad \quad = t_r\cdots t_2t_1\textrm{ }\textrm{ since} \textrm{ each} \textrm{ transposition} \textrm{ inverts} \textrm{ itself}.\textrm{ }\blacksquare$

Вправа$\PageIndex{8}$

Скільки елементів є в$\mathcal{D}_5$? Опишіть їх геометрично.

Вправа$\PageIndex{9}$

Завершіть доказ теореми$\PageIndex{1}$.

Відповідь

Частина I: Це$\lvert S_k \rvert = k!$ випливає з Правил продуктів.

Частина II:$f$ Дозволяти бути функція визначена на$\{1,2,\textrm{ ...}, n\}$$f(1)=2\text{,}$$f(2)=3\text{,}$$f(3)=1\text{,}$ і$f(j) =j$ for$4\leq j\leq n\text{;}$ і нехай$g$ буде$g(1) = 1\text{,}$$g(2) = 3\text{,}$$g(3) = 2\text{,}$ визначена і$g(j) =j$ для$4\leq j\leq n\text{.}$ Примітка, що$f$ і$g$ є елементами$S_n\text{.}$ наступного , в$(f\circ g)(1) = f(g(1)) = f(1) = 2\text{,}$ той час як$(g \circ f)(1) = g(f(1)) = g(2) = 3\text{,}$ отже$f\circ g\neq g\circ f$ і не$S_n$ є абелевим для будь-якого$n \geq 3\text{.}$

Вправа$\PageIndex{10}$

Скільки лівих косетів$A_n\text{,}$$n\geq 2$ має?

Вправа$\PageIndex{11}$

Доведіть, що$f\circ r= r^{n-1}\circ f$ в$\mathcal{D}_n\text{.}$

Вправа$\PageIndex{12}$

Доведіть, що плитки головоломки, відповідні$A_{16}\cap \left\{ \left.f \in S_{16} \right| f(16) = 16\right\}$ вирішувані.
Якщо$f(16)\neq 16\text{,}$ як ви можете визначити, чи$f$ вирішувана головоломка?

Вправа$\PageIndex{13}$

Довести, що$S_3$ є$R_3\text{,}$ ізоморфним для групи$3 \times 3$ матриць тура (див. Розділ 11.2 вправи).
Доведіть, що для кожного$n \geq 2\text{,}$$R_n$ є ізоморфним$S_n\text{.}$

Відповідь

Обидві групи є неабелевими і порядку 6; тому вони повинні бути ізоморфними, оскільки існує лише одна така група аж до ізоморфізму. Функція$\theta:S_3\to R_3$ defined by $\begin{array}{cc} \theta(i)=I & \theta\left(f_1\right)=F_1 \\ \theta\left(r_1\right)=R_1 & \theta\left(f_2\right)=F_2 \\ \theta\left(r_2\right)=R_2 & \theta\left(f_3\right)=F_3 \\ \end{array}$ is an isomorphism,
Нагадаємо, що оскільки кожна функція є відношенням, то природно переводити функції в булеві матриці. Припустимо, що$f\in S_n\text{.}$ ми визначимо його образ,$\theta(f)\text{,}$ за допомогою
\ begin {рівняння*}\ theta (f) _ {kj} =1\ textrm {}\ Leftrightarrow\ textrm {} f (j) =k\ end {рівняння*}
$\theta$ Тобто біекція випливає з існування$\theta^{-1}\text{.}$ If$A$ - матриця тура,
\ begin {рівняння*}\ begin {спліт}\ theta^ {-1} (A) (j) =k &\ Стрілка вліворуч\ textrm {}\ textrm {in}\ textrm {стовпець} j\ textrm {з} A\ textrm {з'являється}\ textrm {в}\ textrm {рядок}\\ &\ Стрілка вліворуч A_ {kj} =1\ end {split}\ end {рівняння*}
для $f,g\in S_n\text{,}$
\ begin {рівняння*}\ початок {спліт}\ тета (f\ circ g) _ {kj} = 1 &\ Ліворуч\ textrm {} (f\ circ g) (j) = k\\ &\\ Стрілка вліво\ існує l\ textrm {такий, що} g (j) =l\ textrm {і} (l) =k\ &\ Стрілка вліво\ існує l\ textrm {така, що}\ тета (g) _ {lj} =1\ textrm {і}\ textrm {}\ theta (f) _ {kl} =1\\ &\ Лівопрягалка (\ тета (f)\ тета (g)) _ {kj} =1\ end {split}\ end {рівняння*}
Отже,$\theta$ є ізоморфізмом.

\(i =\left( \begin{array}{ccc} 1 & 2 & 3 \\ 1 & 2 & 3 \\ \end{array} \right)\)	\(r_1=\left( \begin{array}{ccc} 1 & 2 & 3 \\ 2 & 3 & 1 \\ \end{array} \right)\)	\(r_2=\left( \begin{array}{ccc} 1 & 2 & 3 \\ 3 & 1 & 2 \\ \end{array} \right)\)
\(f_1=\left( \begin{array}{ccc} 1 & 2 & 3 \\ 1 & 3 & 2 \\ \end{array} \right) \)	\(f_2=\left( \begin{array}{ccc} 1 & 2 & 3 \\ 3 & 2 & 1 \\ \end{array} \right)\)	\(f_3=\left( \begin{array}{ccc} 1 & 2 & 3 \\ 2 & 1 & 3 \\ \end{array} \right)\)